Stochastic Dynamics of Proteins and the Action of Biological Molecular Machines
Abstract
: It is now well established that most if not all enzymatic proteins display a slow stochastic dynamics of transitions between a variety of conformational substates composing their native state. A hypothesis is stated that the protein conformational transition networks, as just as higher-level biological networks, the protein interaction network, and the metabolic network, have evolved in the process of self-organized criticality. Here, the criticality means that all the three classes of networks are scale-free and, moreover, display a transition from the fractal organization on a small length-scale to the small-world organization on the large length-scale. Good mathematical models of such networks are stochastic critical branching trees extended by long-range shortcuts. Biological molecular machines are proteins that operate under isothermal conditions and hence are referred to as free energy transducers. They can be formally considered as enzymes that simultaneously catalyze two chemical reactions: the free energy-donating (input) reaction and the free energy-accepting (output) one. The far-from-equilibrium degree of coupling between the output and the input reaction fluxes have been studied both theoretically and by means of the Monte Carlo simulations on model networks. For single input and output gates the degree of coupling cannot exceed unity. Study simulations of random walks on model networks involving more extended gates indicate that the case of the degree of coupling value higher than one is realized on the mentioned above critical branching trees extended by long-range shortcuts.PACS Classification: 05.70.Ln, 87.15.hp, 87.15.Ya, 89.75,Hc1. Enzymatic Proteins–Change of the Fundamental Paradigm
Proteins are linear polymers of amino acids arranged in a sequence determined by genes. Since the origin of molecular biology in the 1950s, a paradigm has been commonly accepted, expressed shortly in two successive implications:
It assumes implicitly that the dynamics of native proteins reduces to simple normal vibrations about a single conformational state referred to as the “tertiary structure” of the protein. For at least two decades, however, it becomes more and more clear that not only structure but also more complex dynamics determine the function of proteins thus the paradigm has to be extended to [1]
Two classes of experiments imply directly that besides fast vibrations enzymatic proteins display also a much slower stochastic dynamics of transitions between a variety of conformational substates composing their native state. The first class includes observations of the non-exponential initial stages of reactions after special preparation of an initial microscopic state in a statistical ensemble of biomolecules by, e.g., the laser pulse [2,3]. The second class concerns statistics of the dichotomous noise generated by single biomolecules in various processes, which often displays a non-exponential time course [4,5]. The even more convincing proof of the conformational transition dynamics of simple native proteins has been afforded by early molecular dynamics simulations [6,7]. Research of biomolecular dynamics is being developed faster and faster and today, even in the case of small, water-soluble proteins, one speaks about the “native state ensemble”, and for very small proteins or protein fragments trials to reconstruct the actual networks of conformational transitions are realized (see papers cited in Reference [8]).
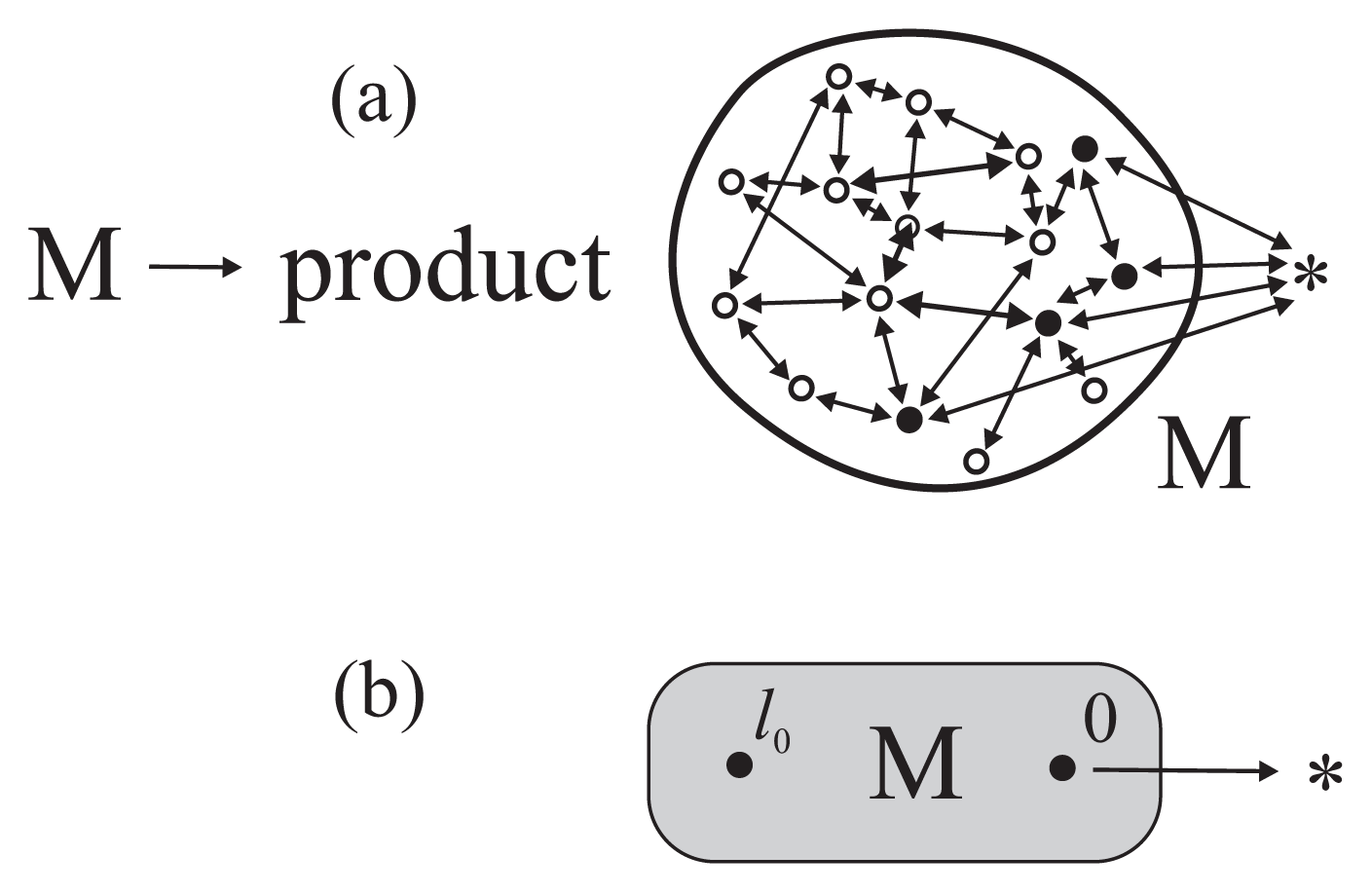
Because of the slow character of the conformational dynamics, both the chemical and conformational transitions in an enzymatic protein have to be treated on an equal footing [9] and jointly described by a system of coupled master equations
determining the time variation of the occupation probabilities pl(t) of the individual protein’s substates (Figure 1). In Equation (1)wl′l is the transition probability per unit time from the substate l to l′, and the dot denotes the time derivative. The conformational transition probabilities satisfy the detailed balance condition which, however, can be broken for the chemical transition probabilities controlled by the concentrations of the enzyme substrates. Equations (1) are to be treated as a model of microscopic dynamics in the stochastic theory of reaction rates [10,11] the origins of which go back to the Smoluchowski theory of diffusion-controlled coagulation and the Kramers one-dimensional theory of reactions in the overdamped limit. It is the stochastic theory of reaction rates and not the conventional transition state theory that should be applied in the description and interpretation of biochemical processes [9,12].
Contrary to the transition state theory, the stochastic theory of reaction rates takes into account the very process of reaching the partial thermodynamic equilibrium in the non-chemical degrees of freedom of the system described. In the closed reactor, the possibility of a chemical transformation of an enzyme will proceed before the conformational equilibrium has been reached results in the presence of a transient non-exponential stage of the process and in an essential dynamical correction to the reaction rate constant describing the following exponential stage [9,11]. In the open reactor under stationary conditions (the concentrations of reactants and products of the reaction kept constant), the general situation is more complex but for the reactions gated by single transition conformational substates (Figure 1b) a simple analytical theory was proposed [9,13]. A consequence of the slow conformational transition dynamics is that the steady-state kinetics, like the transient stage kinetics, cannot be described in terms of the usual rate constants. This possibility was suggested forty years ago by Blumenfeld [14]. Later on still, we have shown that adequate physical quantities that should be used are the mean first-passage times between distinguished transition substates [9,13]. The subject of the present paper is an application of this formalism to elucidate the action of biological molecular machines.
2. Biological Machines as Chemo-Chemical Free Energy Transducers
The primary purpose of thermodynamics, born in the first half of the 19th century, was to explain the action of the heat engines. The processes they are involved in are practically reversible and proceed in varying temperatures. As a consequence, thermodynamics being the subject of the school and academic teaching, still deals mainly with equilibrium processes and changes of temperature. However, biological machines as well as many other contemporary machines act irreversibly, with considerable dissipation, but at constant temperature. Machines that operate under the condition T = const. are free energy transducers [12]. A good example are the enzymes kinases that catalyze simultaneously two reactions, the adenosine triphosphate (ATP) hydrolysis and a substrate phosphorylation.
From a theoretical point of view, it is convenient to treat all biomolecular machines, also pumps and motors, as chemo-chemical machines [12], enzymes that simultaneously catalyze two chemical reactions: the free energy-donating reaction and the free energy-accepting one. Indeed, the molecules present on either side of a biological membrane can simply be considered to occupy different chemical states, whereas the external load influences the free energy involved in binding the motor to its track, which can be expressed as a change of an effective concentration of this track. Under isothermal conditions, all chemical reactions proceed due to thermal fluctuations: a free energy needed for their realization is borrowed from the environment and then returned to it. In fact, most biological molecular machines are the powered Maxwell demons: their mechanical or electrical elements are “soft” and perform work at the expense of thermal fluctuations [15–17]. Of course, Maxwell’s demon can operate only out of equilibrium and it is a task of the free energy-donating reaction to secure such conditions.
The principle of the action of the chemo-chemical machine is simple [18]. It is a protein enzyme that catalyzes simultaneously two chemical reactions (Figure 2a). Separately, each reaction takes place in the direction determined by the second law of thermodynamics, i.e., the condition that energy dissipated, determined by the product of flux and force, is positive. However, if both reactions take place simultaneously in a common cycle, they must proceed in the same direction and the direction of the first reaction can force a change of direction of the second. As a consequence, the first reaction transfers a part of its free energy recovered from dissipation performing work on the second reaction.
In formal terms, the chemo-chemical machine couples two unimolecular reactions: the free energy-donating reaction R1 ↔ P1 and the free energy-accepting reaction R2 ↔ P2. Bimolecular reactions can be considered as effective unimolecular reactions upon assuming a constant concentration of one of the reagents, e.g., adenosine diphosphate (ADP) in the case of ATP hydrolysis. The input and output fluxes Ji (i = 1 and 2, respectively) and the conjugate thermodynamic forces Ai are defined as [18]
and
Here, symbols of the chemical compounds in the square brackets denote the molar concentrations in the steady state (no superscript) or in the equilibrium (the superscript eq). [E]0 is the total concentration of the enzyme and β is proportional to the reciprocal temperature, β ≡ (kBT)−1, where kB is the Boltzmann constant. The flux-force dependence is one-to-one only if some constraints are put on the concentrations [Ri] and [Pi] for each i. There are two possibilities. Either the concentration of one species, say Ri, in the open reactor under consideration is kept constant: [Ri] = const., or it is the total concentration of the enzyme substrate: [Ri] + [Pi] = const.
The free energy transduction is realized if the product J2A2, representing the output power, is negative. The efficiency of the machine is the ratio
of the output power to the input power. In general, the degree of coupling of both fluxes,
being itself a function of the forces A1 and A2, can be both positive or negative. To avoid a misconception, let us stress that the definition (5) does not coincide with the former definition of the degree of coupling for the linear case (which usually does not apply to biomolecular processes) by Kedem and Caplan [19]. In more details, upon introducing the Onsager kinetic coefficients Lij = Lji, the linear approximation for Equation (5) reads
where
are the Kedem-Caplan degree of coupling and the stoichiometric force ratio [20,21], respectively.
Usually, the assumption of tight coupling between both reactions is made (Figure 2a). It states that the flux of the first reaction equals the flux of the second, J1 = J2, thus ε = 1. However, an additional reaction can take place between the two states M′ and M″ of the enzyme-substrates complex (Figure 2b). The latter reaction can be considered either as a short circuit, the non-productive realization of the first reaction not driving the second reaction, or a slippage, the realization of the second reaction in the direction dictated by its conjugate force.
The multiconformational counterpart of the scheme in Figure 2b is shown in Figure 2c. Here, as in the scheme in Figure 1b, a network of conformational transitions within the enzyme-substrates complex is represented by the gray box and the assumption of gating by single pairs of transition conformational substates is made. In Reference [13], using a technique of summing up the directional diagrams proposed by Terell L. Hill [18] who formalized a former idea of Gustav Kirchhoff, we showed how the input and output reaction fluxes are related to the mean first-passage times between the distinguished substates.
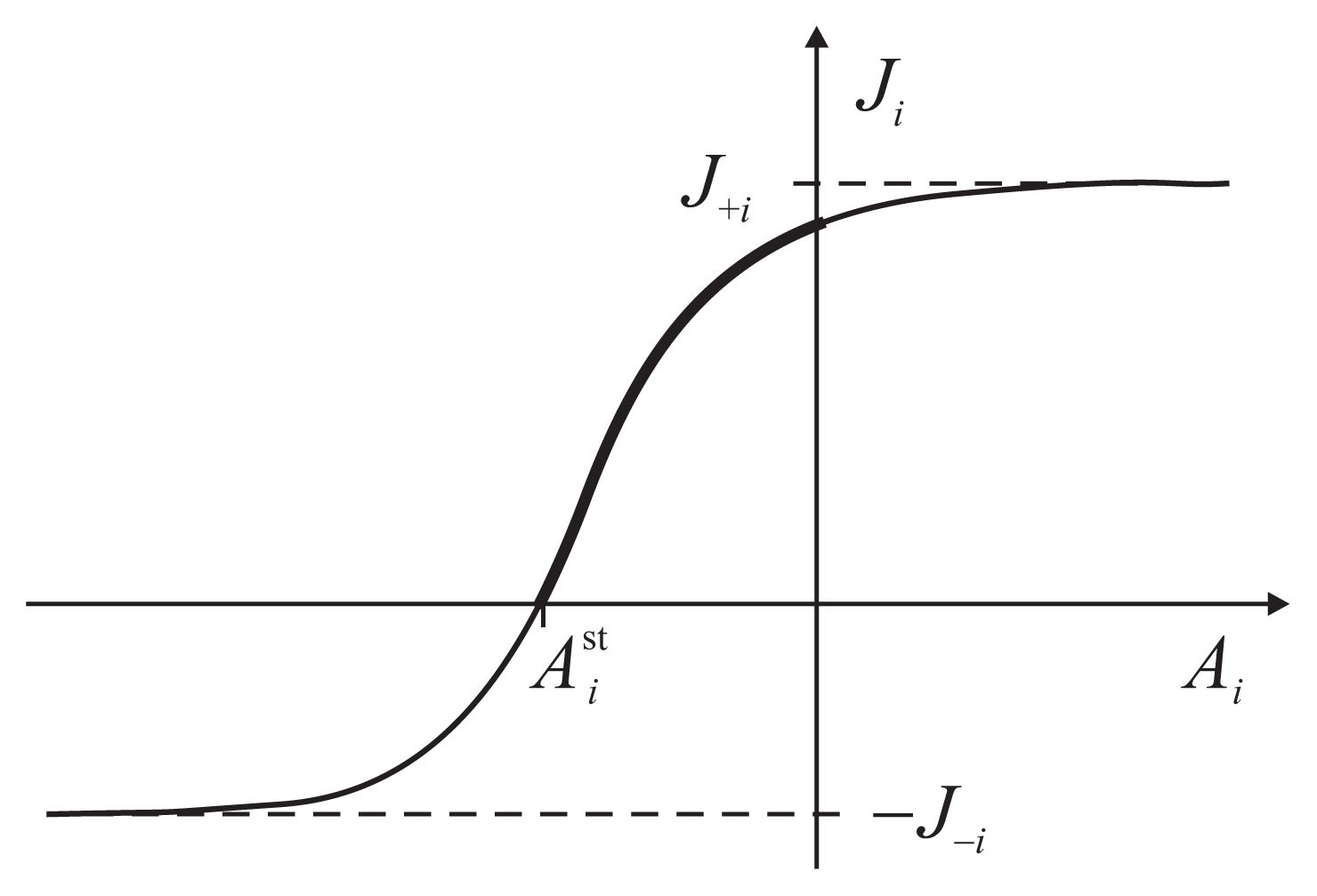
The flux-force dependence thus obtained for the two coupled reactions has a general functional form
The parameters J+i, J−i, J0i and depend on the other force and are determined by a particular kinetic scheme, i.e., the interior of the gray box. have the meaning of stalling forces for which the fluxes Ji vanish: . The efficiency Equation (4) is zero both for A2 = 0 and for . The dependence Ji(Ai) is strictly increasing with an inflection point, determined by J0i, and two asymptotes, J+i and J−i (Figure 3). The asymptotic fluxes J+i and J−i display the Michaelis-Menten dependence on the substrate concentrations. The relatively simple formulas for the degree of coupling ε and the stalling forces are given and discussed in Reference [8].
In Reference [8], we have compared the theoretical results with the Monte Carlo simulations on several model networks. Figure 4 shows an example of the fluxes for 5-dimensional hypercube with constant transition probabilities. It is seen that even for such simple and small network of 32 nodes, large fluctuations make determination of the input and the output mean fluxes in 104 iteration steps impossible. Only by increasing the number of the iteration steps to 109 can one determine the fluxes, thus their degree of coupling, with the error lower than 0.3%. Preliminary estimations indicate that the result is in a good agreement with the stationary fluctuation theorem [22–25] in the Andrieux-Gaspard form [26]:
which can be equivalently rewritten as
Above, p is the joint probability distribution function for the statistical ensamble of the fluxes, in general being not factorized:
and 〈. . .〉 is the average over that ensemble.
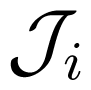
3. Networks of Conformational Transitions and Critical Branching Trees
The essential motive of our studies is a trial to answer the intriguing question of whether is it possible for the degree of coupling Equation (5) to have a value higher than unity. A dogma in the physical theory of, e.g., biological molecular motors, is the assumption that for making a single step along its track the motor molecule has to hydrolyze at least one molecule of ATP [27]. Several years ago this assumption was questioned by a group of Japanese biophysicists from the Yanagida laboratory who, joining a specific nanometry technique with the microscopy fluorescence spectroscopy, shown that the myosin II head can make several steps along the actin filament per ATP molecule hydrolyzed [28,29]. The structure of the myosin II is similar to that of small G proteins, e.g., the protein Ras (rat sarcoma) p21, both classes of proteins having a common ancestor [30]. Both in the G proteins [31] and in the myosin II [32,33] one of the α helices unwinds in part after binding the nucleotide triphosphate, which makes the neighboring region partly disordered, highly flexible, thus fluctuating. The detachment of the motor molecule from its track corresponds to the attachment of the signal transducting G protein to its effector. As a consequence, taking several steps per ATP molecule hydrolyzed by myosin II could correspond to the activation of many effectors per GTP molecule hydrolyzed by a malignantly mutated oncogene Ras protein. Also in the transcription factor p53, the DNA binding core domain is partly disordered [34]. The commonly assumed model of facilitated, alternating three- and one-dimensional passive diffusion, does not explain all the known facts concerning the search for a proper biding site on DNA [35], so a hypothesis that this search can be active, using the free energy of a single ATP molecule hydrolysis many times, seems reasonable.
No conventional chemical kinetics approach is able to explain such behaviors. In References [13] and [12], basing on approximations carried too far, we suggested that the far-from-equilibrium degree of coupling can exceed unity already for reactions proceeding through single pairs of transition substates. In Reference [8], we proved the theorem that the value of the degree of coupling (5) should be lower than, or at the most equal to, unity, but only when the input and output reactions proceed through single pairs of transition conformational substates. It is reasonable to suppose that the chance of a higher degree of coupling is possible if the output gate is extended to two or more pairs of transition substates (Figure 2d). Unfortunately, even in the case of only two output gates the analytical formulas are so complex and not transparent that serious approximations are needed to be made from the very beginning. Not being able to formulate presently such approximations, we decided to apply computer experiment for a preliminary study of the problem.
Since the formulation by Bak and Sneppen a cellular automaton model of the Eldredge and Gould punctuated equilibriums [36], the biological evolution is more and more often considered as a self-organized criticality phenomenon [37,38]. There are grounds to suppose that the conformational transition networks, as just as the two networks of the systems biology, the protein interaction network, and the metabolic network, have evolved to reach a scale-free, thus critical structure [8]. A controversy emerges if this structure is simulaneously fractal or small-world. The topological structure of a flow (of probability, metabolites, energy or information) through a network is characterized by a spatial spanning tree composed of the most conducting links not involved in cycles. It is referred to as the skeleton [39] of the network, all the rejected links being considered as shortcuts. The skeleton of the scale-free and fractal network is also scale-free and fractal. For the scale-free fractal trees a criticality feature appears important that denotes the presence of a plateau equal to unity in the mean branching number dependence on the distance from the skeleton root. The critical trees can be completed to fractal scale-free networks [39]. Only recently has an apparent contradiction between fractality and small-worldness been explained by the application of the renormalization group technique [40]. It appears that, upon adding shortcuts with the distance r distribution fulfilling the power law r−α to an original fractal network, a transition to the small world network occurs below some critical value of the exponent α. Close to this critical value the network can be fractal in a small length-scale, simultaneously having the small-world features in the large length-scale and this is the case of the protein interaction network, the metabolic network and, probably, the protein conformational transition network as well.
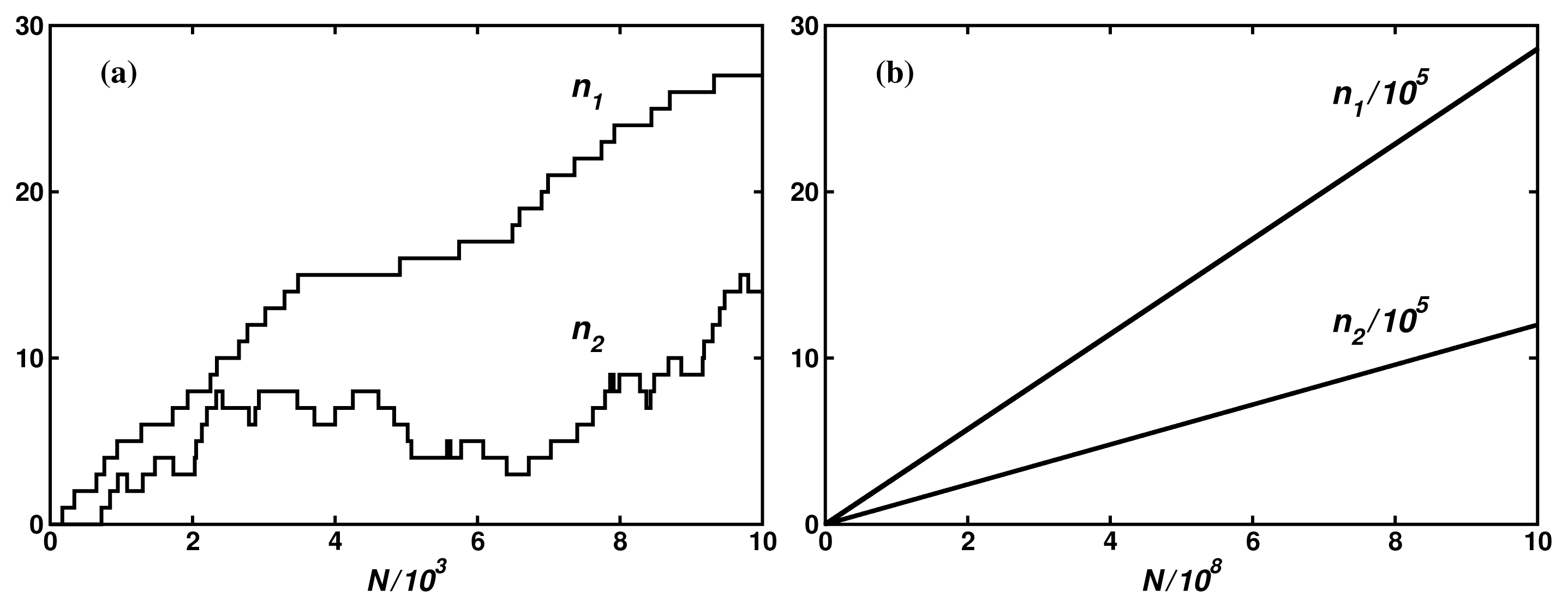
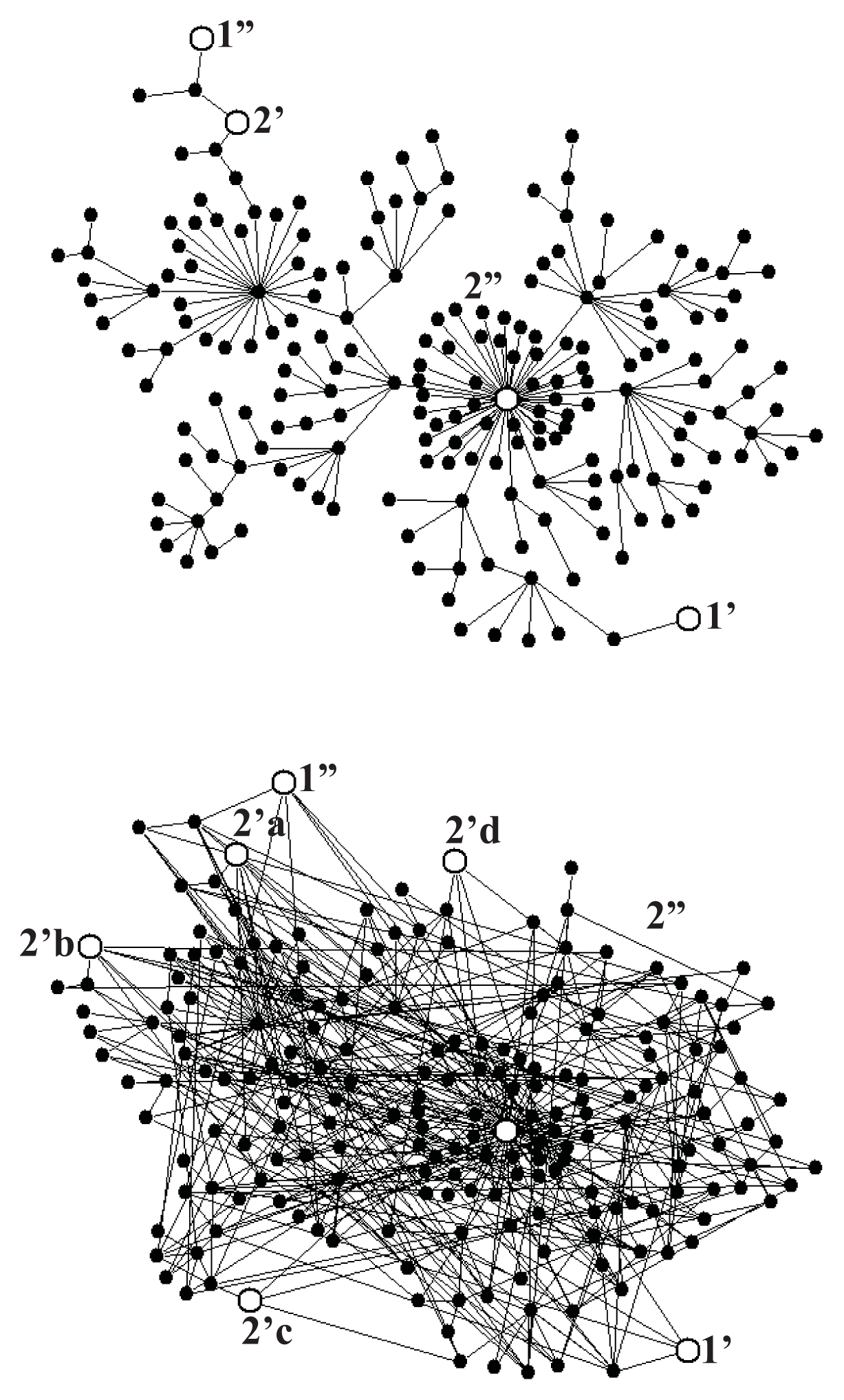
Figure 5a shows a scale-free fractal tree with N = 200 nodes constructed following the algorithm described in Reference [39], and Figure 5b shows an extension of this tree by 200 shortcuts with the distance distribution fulfilling the power law r2, with negative α, which makes the network a scale-free small world. To provide the network with a stochastic dynamics described by Equation (1), we assume the probability of changing a node to any of its neighbors to be the same in each random walk step. Consequently, the transition probability from the node l to the neighboring node l′ per the computer step is
where kl is the number of links (the degree) of the node l. The network with such a dynamics cannot be isoenergetic and following the detailed balance principle the equilibrium occupation probability of the node l is
For the system of gates as shown in Figure 5a, we performed a series of Monte Carlo simulations for A2 = 0, and found ε = 0.99 for mean times of external transitions τ1 = τ2 = 40 computer steps, those times being one order of magnitude shorter than the internal relaxation time τrx = 400 which means that the input and output reactions were controlled, though not completely, by intramolecular dynamics. The case of multiple output gates needs more systematic studies. For the system of gates shown in Figure 5b and τ1 = τ2 = 40 we found ε = 1.40, a value larger than unity. Random search for more optimal configuration of gates indicates a possibility of obtaining much higher value of the degree of coupling.
To end of the paper, it is worth presenting the scale of fluctuations for the dynamics discussed. Figure 6a shows the probability distribution functions for the statistical ensambles of the input fluxes

Figure 6a shows that, up to a numerical error, the steady-state fluctuation theorem is satisfied for both networks. The deviation from the second law of thermodynamics increases with a decrease of the time period t of the flux averaging, the distance βA from the equilibrium, and the number N of the network nodes. The number of links (compare Figure 5a with Figure 5b does not influence that deviation but increases only a dispersion of the fluctuations.
4. Summary
It is now well established that most if not all enzymatic proteins display a slow stochastic dynamics of transitions between a variety of conformational substates composing their native state. This makes the possibility of chemical transformations to proceed before the conformational equilibrium has been reached in the actual chemical state. In the closed reactor, it results in the presence of transient, non-exponential stages of the reactions. In the open reactor, a consequence is the necessity of determining the steady-state reaction fluxes by the mean first-passage times between transition conformational substates of the reactions rather than by conventional reaction rate constants. A hypothesis is stated that, as just as higher level biological networks, the protein interaction network, and the metabolic network, the protein conformational transition networks have evolved in a process of self-organized criticality. All the three classes of networks are scale-free and, probably, display a transition from the fractal organization on a small length-scale to the small-world organization on a large length scale. Good mathematical models of such networks are stochastic critical branching trees extended by long-range shortcuts.
Biological molecular machines are proteins that operate under isothermal conditions and hence are referred to as free energy transducers. They can be formally considered as enzymes that simultaneously catalyze two chemical reactions: the free energy-donating (input) reaction and the free energy-accepting (output) one. The far-from-equilibrium degree of coupling between the output and the input reaction fluxes have been studied both theoretically and by means of the Monte Carlo simulations on model networks. In the steady state, upon taking advantage of the assumption that each reaction proceeds through a single pair (the gate) of transition conformational substates of the enzyme-substrates complex, the degree of coupling between the output and the input reaction fluxes has been expressed in terms of the mean first-passage times on a conformational transition network between the distinguished substates. The theory has been confronted with the results of random walk simulations on various model networks.
For single input and output gates, the degree of coupling cannot exceed unity. As some experiments for the myosin II motor suggest such exceeding, looking for the conditions for increasing the degree of coupling value over unity (realization of a “molecular gear”) challenges the theory. Probably it holds also for the G-proteins and transcription factors, mutations of which can result in the cancerogenesis. Study simulations of random walks on several model networks involving more extended gates indicate that the case of the degree of coupling with the value higher than one is realized in a natural way on critical branching trees extended by long-range shortcuts. For short-range shortcuts, the networks are scale-free and fractal, and represent reasonable models for biomolecular machines displying tight coupling, i.e., the degree of coupling value close to unity.
Acknowledgments
The study has been supported in part by the Polish Ministry of Science and Higher Education (project N N202 180038).
Conflicts of Interest
The authors declare no conflicts of interest.
- Author ContributionsBoth authors equally contributed to the paper. The general conception and the theory is mainly due to MK, who also wrote the manuscript. The application of the critical branching tree model and numerical simulations are mainly due to PC. The authors approved the final version of the manuscript.
References
- Chouard, T. Breaking the protein rules. Nature 2011, 471, 151–153. [Google Scholar]
- Austin, R.H.; Beeson, K.W.; Eisenstein, L.; Frauenfelder, H.; Gunsalus, I.C. Dynamics of ligand binding to myoglobin. Biochemistry 1975, 14, 5355–5373. [Google Scholar]
- Frauenfelder, H.; Sligar, S.G.; Wolynes, F.G. The energy landscapes and motions of proteins. Science 1991, 254, 1598–1602. [Google Scholar]
- Sansom, M.P.S.; Ball, F.G.; Kerry, C.J.; McGee, R.; Ramsey, R.L.; Usherwood, P.N. Markov, fractal, diffusion, and related models of ion channel gating. A comparison with experimental data from two ion channels. Biophys. J 1989, 56, 1229–1243. [Google Scholar]
- Kurzynski, M. Statistical properties of the dichotomous noise generated in biochemical processes. Cell. Mol. Biol. Lett 2008, 13, 502–513. [Google Scholar]
- Garcia, A.E.; Blumenfeld, R.; Hummer, G.; Krumhansl, J.A. Multi-basin dynamics of a protein in a crystal environment. Phys. D 1997, 107, 225–239. [Google Scholar]
- Kitao, A.; Hayward, S.; Gō, N. Energy landscape of a native protein: Jumping-among-minima model. Proteins 1998, 33, 496–517. [Google Scholar]
- Kurzynski, M.; Torchala, M.; Chelminiak, P. Output-input ratio in thermally fluctuating biomolecular machines. Phys. Rev. E 2014, 89, 012722. [Google Scholar]
- Kurzynski, M. A synthetic picture of intramolecular dynamics of proteins. Towards a contemporary statistical theory of biochemical processes. Progr. Biophys. Mol. Biol 1998, 69, 23–82. [Google Scholar]
- Widom, B. Molecular transitions and chemical reaction rates. Science 1965, 148, 1555–1560. [Google Scholar]
- Northrup, S.H.; Hynes, J.T. The stable states picture of chemical reactions. J. Chem. Phys 1980, 73, 2700–2714. [Google Scholar]
- Kurzynski, M. The Thermodynamic Machinery of Life; Springer: Berlin, Germany, 2006. [Google Scholar]
- Kurzynski, M.; Chelminiak, P. Mean first-passage time in stochastic theory of biochemical processes. Application to actomyosin molecular motor. J. Stat. Phys 2003, 110, 137–181. [Google Scholar]
- Blumenfeld, L.A. Problems of Biological Physics; Springer-Verlag: Berlin, Germany, 1981. [Google Scholar]
- Vale, R.D.; Oosawa, F. Protein motors and Maxwell’s demons: Does mechanochemical transduction involve a thermal ratchet? Adv. Biophys 1990, 26, 97–134. [Google Scholar]
- Jones, R.A.L. Soft Machines, Nanotechnology and Life; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Yanagida, T.; Ueda, M.; Murata, T.; Esaki, S.; Ishii, Y. Brownian motion, fluctuation and life. BioSystems 2007, 88, 228–242. [Google Scholar]
- Hill, T. L. Free Energy Transduction and Biochemical Cycle Kinetics; Springer: New York, NY, USA, 1989. [Google Scholar]
- Kedem, O.; Caplan, S.R. Degree of coupling and its relation to efficiency of energy converters. Tans. Faraday Soc 1965, 61, 1897–1911. [Google Scholar]
- Stucki, J.W. The optimal efficiency and the economic degrees of coupling of oxidative phosphorylation. Eur. J. Biochem 1980, 109, 269–283. [Google Scholar]
- Demirel, Y. Nonequilibrium thermodynamics modeling of coupled biochemical cycles in living cells. J. Non-Newtonian Fluid Mech 2010, 165, 953–972. [Google Scholar]
- Crooks, G.E. Entropy production fluctuation theorem and the nonequilibrium work relation for free energy differences. Phys. Rev. E 1999, 60, 2721–2726. [Google Scholar]
- Searles, D.J.; Evans, D.J. The fluctuation theorem for stochastic systems. Phys. Rev. E 1999, 60, 159–164. [Google Scholar]
- Dewar, R.C. Maximum entropy production and the fluctuation theorem. J. Phys. A: Math. Gen 2005, 38, L372–L381. [Google Scholar]
- Demirel, Y. Nonequilibrium Thermodynamics: Transport and Rate Processes in Physical, Chemical and Biological Systems, 3rd ed; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Andrieux, D.; Gaspard, P. Fluctuation theorem for currents and Schnakenberg network theory. J. Stat. Phys 2007, 127, 107. [Google Scholar]
- Howard, J. Mechanics of Motor Proteins and the Cytoskeleton; Sinauer: Sunderland, MA, USA, 2001. [Google Scholar]
- Kitamura, K.; Tokunaga, M.; Iwane, A.H.; Yanagida, T. A single myosin head moves along an actin filament with regular steps of 5.3 nanometers. Nature 1997, 397, 129–134. [Google Scholar]
- Kitamura, K.; Tokunaga, M.; Esaki, S.; Iwane, A.H.; Yanagida, T. Mechanism of muscle contraction based on stochastic properties of single actomyosin motors observed in vitro. Biophysics 2005, 1, 1–19. [Google Scholar]
- Kull, F.J.; Vale, R.D.; Fletterick, R.J. The case for a common ancestor: kinesin and myosin motor proteins and G proteins. J. Muscle Res. Cell Motil 1998, 19, 877–886. [Google Scholar]
- Kosztin, I.; Bruinsma, R.; O’Lague, P.; Schulten, K. Mechanical force generation by G proteins. Proc. Natl. Acad. Sci. USA 2002, 99, 3575–3580. [Google Scholar]
- Xu, J.; Root, D.D. Conformational selection during weak binding of the actin and myosin interface. Biophys. J 2000, 79, 1498–1510. [Google Scholar]
- Houdusse, A.; Sweeney, H.L. Myosin motors: Missing structures and hidden springs. Curr. Res. Struct. Biol 2001, 11, 182–194. [Google Scholar]
- Joerger, A.C.; Fersht, A.R. Structural biology of the tumor suppressor p53. Annu. Rev. Biochem 2008, 77, 557–582. [Google Scholar]
- Kolomeisky, A.B. Physics of protein-DNA interactions: Mechanisms of facilitated target search. Phys. Chem. Chem. Sol 2011, 13, 2088. [Google Scholar]
- Bak, P.; Sneppen, K. Punctuated equilibrium and criticality in simple model of evolution. Phys. Rev. Lett 1993, 71, 4083–4086. [Google Scholar]
- Bak, P. How Nature Works: The Science of Self-Organized Criticality; Copernicus Press: New York, NY, USA, 1996. [Google Scholar]
- Sneppen, K.; Zocchi, G. Physics in Molecular Biology; Cambridge University Press: New York, NY, USA, 2005. [Google Scholar]
- Goh, K.I.; Salvi, G.; Kahng, B.; Kim, D. Skeleton and fractal scaling in complex networks. Phys. Rev. Lett 2006, 96, 018701. [Google Scholar]
- Rozenfeld, H.D.; Song, C.; Makse, H.A. Small-world to fractal transition in complex networks: A renormalization group approach. Phys. Rev. Lett 2010, 104, 025701. [Google Scholar]

 (t) averaged over the time period t = 5 × 103 computer steps, determined for the input force βA1 = 0.3 and the output force βA2 = 0. The circles represent data for the fractal tree network (Figure 5a) and the squares, for the small-world network (Figure 5b). The continuous lines represent fits to the normal distributions; (b) Fulfilment of the linear relation (14) for both the fractal tree (the circles) and the small-world network (the squares).
(t) averaged over the time period t = 5 × 103 computer steps, determined for the input force βA1 = 0.3 and the output force βA2 = 0. The circles represent data for the fractal tree network (Figure 5a) and the squares, for the small-world network (Figure 5b). The continuous lines represent fits to the normal distributions; (b) Fulfilment of the linear relation (14) for both the fractal tree (the circles) and the small-world network (the squares).
 (t) averaged over the time period t = 5 × 103 computer steps, determined for the input force βA1 = 0.3 and the output force βA2 = 0. The circles represent data for the fractal tree network (Figure 5a) and the squares, for the small-world network (Figure 5b). The continuous lines represent fits to the normal distributions; (b) Fulfilment of the linear relation (14) for both the fractal tree (the circles) and the small-world network (the squares).
(t) averaged over the time period t = 5 × 103 computer steps, determined for the input force βA1 = 0.3 and the output force βA2 = 0. The circles represent data for the fractal tree network (Figure 5a) and the squares, for the small-world network (Figure 5b). The continuous lines represent fits to the normal distributions; (b) Fulfilment of the linear relation (14) for both the fractal tree (the circles) and the small-world network (the squares).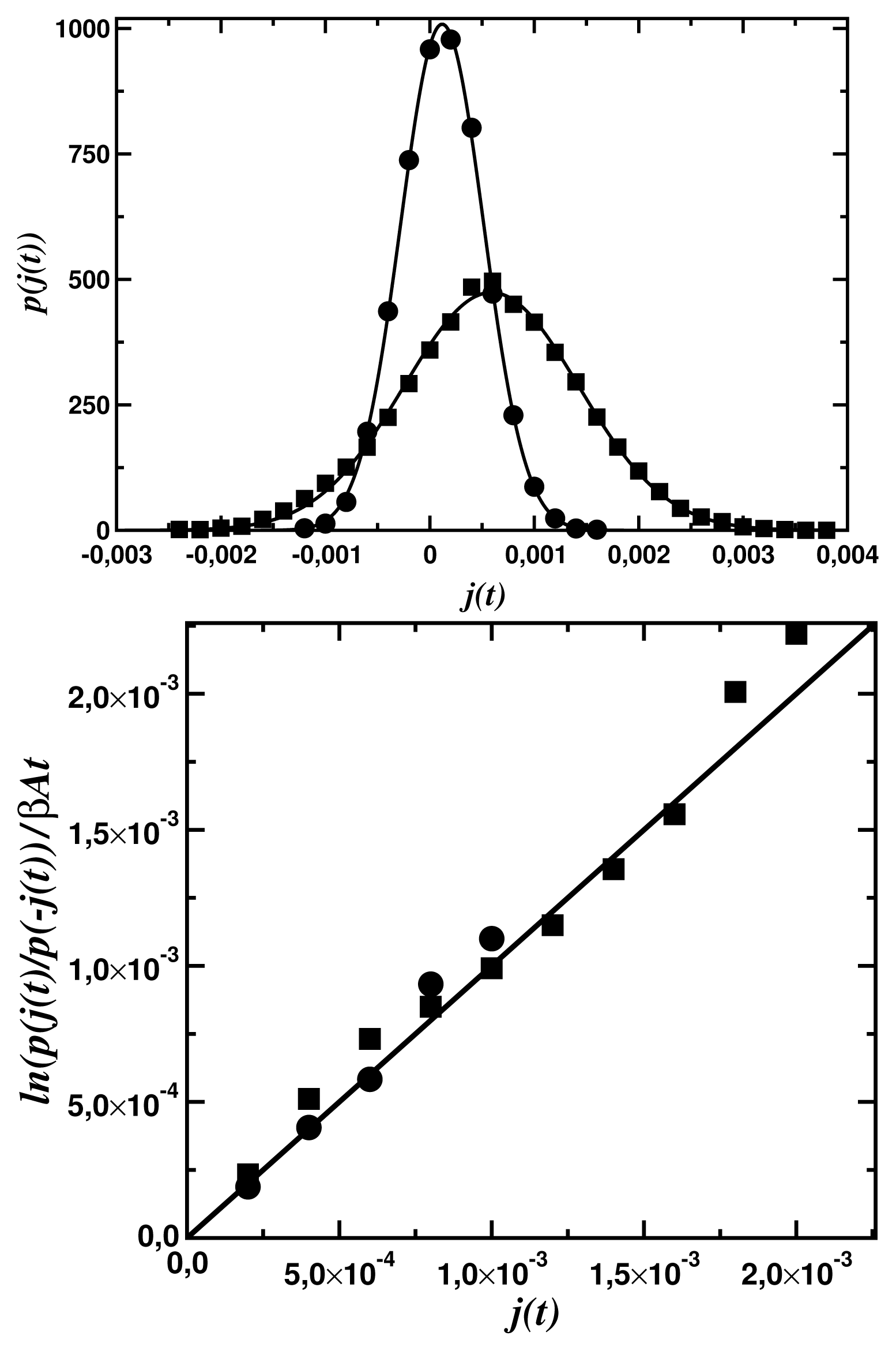
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kurzynski, M.; Chelminiak, P. Stochastic Dynamics of Proteins and the Action of Biological Molecular Machines. Entropy 2014, 16, 1969-1982. https://doi.org/10.3390/e16041969
Kurzynski M, Chelminiak P. Stochastic Dynamics of Proteins and the Action of Biological Molecular Machines. Entropy. 2014; 16(4):1969-1982. https://doi.org/10.3390/e16041969
Chicago/Turabian StyleKurzynski, Michal, and Przemyslaw Chelminiak. 2014. "Stochastic Dynamics of Proteins and the Action of Biological Molecular Machines" Entropy 16, no. 4: 1969-1982. https://doi.org/10.3390/e16041969



