Approximating Time-Dependent Quantum Statistical Properties
Abstract
: Computing quantum dynamics in condensed matter systems is an open challenge due to the exponential scaling of exact algorithms with the number of degrees of freedom. Current methods try to reduce the cost of the calculation using classical dynamics as the key ingredient of approximations of the quantum time evolution. Two main approaches exist, quantum classical and semi-classical, but they suffer from various difficulties, in particular when trying to go beyond the classical approximation. It may then be useful to reconsider the problem focusing on statistical time-dependent averages rather than directly on the dynamics. In this paper, we discuss a recently developed scheme for calculating symmetrized correlation functions. In this scheme, the full (complex time) evolution is broken into segments alternating thermal and real-time propagation, and the latter is reduced to classical dynamics via a linearization approximation. Increasing the number of segments systematically improves the result with respect to full classical dynamics, but at a cost which is still prohibitive. If only one segment is considered, a cumulant expansion can be used to obtain a computationally efficient algorithm, which has proven accurate for condensed phase systems in moderately quantum regimes. This scheme is summarized in the second part of the paper. We conclude by outlining how the cumulant expansion formally provides a way to improve convergence also for more than one segment. Future work will focus on testing the numerical performance of this extension and, more importantly, on investigating the limit for the number of segments that goes to infinity of the approximate expression for the symmetrized correlation function to assess formally its convergence to the exact result.1. Introduction
Exact simulation methods to compute either the evolution of the wave function or dynamical statistical averages for quantum systems in the condensed phase are currently restricted to small sizes and short times. The exponential scaling of available algorithms with the number of degrees of freedom, in fact, limits calculations to ten–twenty particles (and this for Hamiltonians of relatively simple form) and to time scales of at most a few picoseconds. This situation is in striking contrast with analogous classical calculations, which, when empirical potentials are adopted, are nowadays routinely used to study high dimensional, complex systems for times reaching, on dedicated machines, microseconds. (Ab initio classical molecular dynamics is considerably more expensive, but, depending on the number of electrons that have to be included, even in this case moderately sized systems of up to a hundred particles can be integrated for hundreds of picoseconds.) Several approximate schemes have thus been proposed attempting to import, with appropriate modifications, methods from classical molecular dynamics to quantum dynamics. Two approaches, in particular, can be identified in which classical trajectories play a crucial role: semi-classical and mixed quantum classical.
In semi-classical schemes, originally developed for approximating wave function propagation, all degrees of freedom are treated on equal footings. To begin with, the quantum time propagator is expressed, in the path integral formalism [1], as a sum over all possible paths connecting the initial and final states, each path being weighted by a complex exponential, whose argument is the classical action along it. The approximate propagator is then obtained by expanding the action to second order around its stationary points, which are classical trajectories, and performing the remaining quadratic path integral analytically [2,3]. Different forms exist for the semi-classical propagator depending on the specific representation adopted for the path integral (most notably standard coordinates, usually followed by the so-called initial value transformation [4,5], hybrid coordinate momenta [6] or coherent states [7–9]), but the evolved wave function has always the same structure, which we illustrate with the most commonly used Herman Kluk expression [10–12]:
In the expression above, |q, p〉 indicates a coherent state (in the coordinate representation, 〈 r|q, p〉 ∝ e−γ(q−r)2+ip(q−r)/ℏ), Scl(t) is the action computed along a classical trajectory propagated to time t from initial conditions (q, p), (q(t), p(t)) is the endpoint of the trajectory and W (t), a known function, is the result of the integration over the quadratic fluctuations around the stationary paths. All the functions of time in the integrand are calculable using classical evolution algorithms and, once the ket has been saturated (for example, via a scalar product), the integral over the initial conditions can be estimated via Monte Carlo sampling of a probability density based on the absolute value of the wave function at t = 0. Although calculations based on this scheme have been used, the semi-classical wave function is still remarkably expensive, due mainly to the characteristics of W (t). This function is in fact related to a linear combination of the monodromy matrices of the system (i.e., the matrices of the derivatives of the endpoints of the trajectory with respect to the initial conditions), and, for chaotic dynamics, it can assume values varying over several orders of magnitude, hindering the convergence of the Monte Carlo sampling. Furthermore, the actual evaluation of the wave function requires one to project |Ψ(t)〉 sc on a basis. While this is, in principle, straightforward (for example, one could choose the continuous coordinate representation and then discretize it on a grid), in practice it reinstates the exponential scaling of the numerical effort with the number of degrees of freedom. This last problem can be avoided focusing on expected values (observables):
The problems and numerical cost of semi-classical calculations justify the development of the second, alternative approximation scheme mentioned at the beginning of this section: mixed quantum classical dynamics. In this approach, the degrees of freedom of the system are partitioned into two sets, usually based on their mass ratio. The first set (called the subsystem) is composed of a few degrees of freedom and is treated quantum mechanically; the second (called the environment or the bath) is often high dimensional and is treated classically. Existing quantum classical methods differ in the way in which the coupling among the classical evolution of the bath and the quantum propagation of the subsystem is taken into account. The first approach of this kind, still very popular due to its efficiency and ease of implementation, is Tully’s surface hopping [20]. In this scheme, electrons and nuclei constitute the subsystem and the bath, respectively, and the coupling, designed to mimic dynamics beyond the Born–Oppenheimer approximation, is defined ad hoc based on heuristic arguments. In more recent, and more rigorous, developments, the coupling is derived starting from a fully quantum representation of the evolution equations for the system and then taking a partial classical limit on the bath’s degrees of freedom. Examples of this type are schemes to propagate the full density matrix of the quantum subsystem, such as the Wigner Liouville mixed quantum dynamics [21,22], or the iterative linearized density propagation methods [23,24]. Both surface hopping and Wigner Liouville dynamics (with particular reference to its most recent developments aimed at computing correlation functions) are discussed (and/or criticized) in other contributions to this issue. Focusing on the latter, we quickly recall that it adopts a mixed representation in which the operators related to the bath’s degrees of freedom are described using the Wigner representation, while for the subsystem an abstract operator representation is retained. The quantum evolution operator in this mixed representation is then expanded to first order in the ratio of the thermal De Broglie wavelength of subsystem to the bath to obtain the generator of the mixed quantum classical dynamics. This generator has the form of a generalized Lie bracket in which both a commutator (linked to the operators for the subsystem) and Poisson parenthesis (acting on the bath’s phase space) appear. Once a specific basis set is chosen for the subsystem (e.g., adiabatic electronic states [21,25] or, more recently, the so-called mapping representation [26,27]) the evolution equation for the density matrix, or any observable, becomes explicit, and several different algorithms, sharing the characteristic that the bath motion is obtained via classical evolution (possibly with generalized forces describing the influence of more than one electronic state), have been proposed to solve them. In spite of its merits, it has been shown that this mixed quantum classical dynamics lacks several properties that characterize fully quantum and classical dynamics [28]. In particular the mixed Lie bracket does not satisfy the Jacobi identity exactly, and, similar to linearized calculations, the quantum thermal density is not stationary under the mixed dynamics. The loss of formal properties with respect to classical and quantum mechanics arises, in different forms, in all current mixed quantum classical schemes (see also [29]).
While application driven calculations might not be paralyzed by the state of affairs described above, in particular, if and when it is possible to verify that these well-known pathologies have no uncontrolled effects on the results, it is important to pursue alternative approaches in an effort to derive more general schemes allowing for systematic improvement and/or assessment of the approximations employed. Indeed, a critical stumbling block common to semi-classical and mixed quantum classical methods is that it is essentially impossible to go beyond classical trajectories to approximate the quantum evolution of the full system (semi-classical) or of the bath (mixed). In the semi-classical case, including terms of higher order, the expansion of the action along the paths makes it impossible to obtain calculable expressions for the pre-factor in the expression of the wave function (already at third order, the integral corresponds to intractable Airy functions [2]), while in the linearized correlation function, it kills the emergence of delta functions that univocally determine the semi-sum path. In mixed quantum classical calculations, we refer to the Wigner Liouville formalism, but analogous problems appear, for example, in the iterative linearized propagation methods, including higher order terms in the mass ratio expansion of the propagator introduces terms in the phase space evolution of the bath that cannot be integrated numerically. In this paper, we summarize (in the spirit of an extended review) a recently developed method [30] attempting to overcome this problem. In this approach, the focus is not directly on the dynamics, but, rather, on statistical time-dependent averages, which are linked (via linear response theory) to experimental observables. In particular, we focus on time correlation functions expressed in the symmetrized form first introduced by Schofield [31]:
2. Theory
Let us begin by expressing the symmetrized correlation function, Equation (5), in the coordinate representation. Inserting resolutions of the identity, we have:
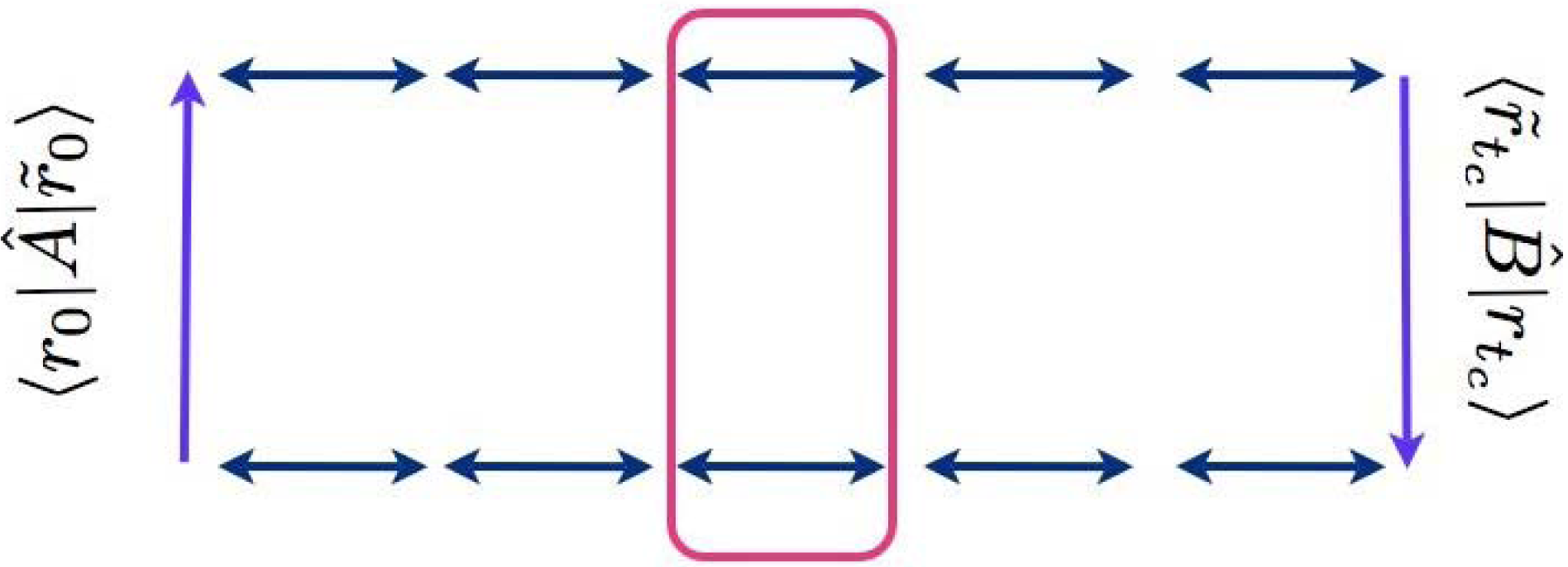
The structure of the integrand is represented in Figure 1 in which we show the sequence of matrix elements to be evaluated. Reading the figure from the bottom left corner up, we see the matrix element of operator Â, the backward complex time propagator (from r̃0 to r̃c), the matrix element of operator B̂ and, finally, the forward propagator that closes the circuit representing the trace operation. The difficult task is the evaluation of the propagators in complex time. To set the stage for the approximation we intend to perform, we use the time composition property to divide the two propagations into L segments of duration τc = tc/L (τc need not be infinitesimal) and rewrite, for example:
The expression above is an exact, incalculable, expression of the time correlation function. In the following, we will work on the generic K to obtain an approximate expression for it that has the key advantage of being analytically known as a product of functions calculable via an appropriate combination of Monte Carlo and molecular dynamics. To obtain this result, we first separate the real from the imaginary time part of the propagation by inserting one more resolution of the coordinate identity, thus:
The linearization approximation then has two crucial consequences: (1) by allowing the integration over the difference paths, it transforms the quantum expression of the correlation function, which, in the beginning, includes two propagators and, therefore, two paths, into a formula where only the semi-sum path appears, thus leading to a structure more similar to classical time correlations in which only one propagation is present; (2) (perhaps more importantly) it forces the semi-sum path to follow a, classical, Hamiltonian trajectory, as identified by the arguments of the delta functions.
The final step to obtain a suitable expression for Equation (9) does not introduce any further approximation. Let us consider again the product of the thermal propagators in the equation. As mentioned above, these can be written via standard coordinate path integrals. Once this is done, it is convenient to introduce also for these propagators semi-sum and difference path (this is important, in particular, to ensure that the common boundaries of the thermal and real-time propagations, and , are represented coherently). In the semi-sum and difference variables, the product of the thermal propagators takes the form:
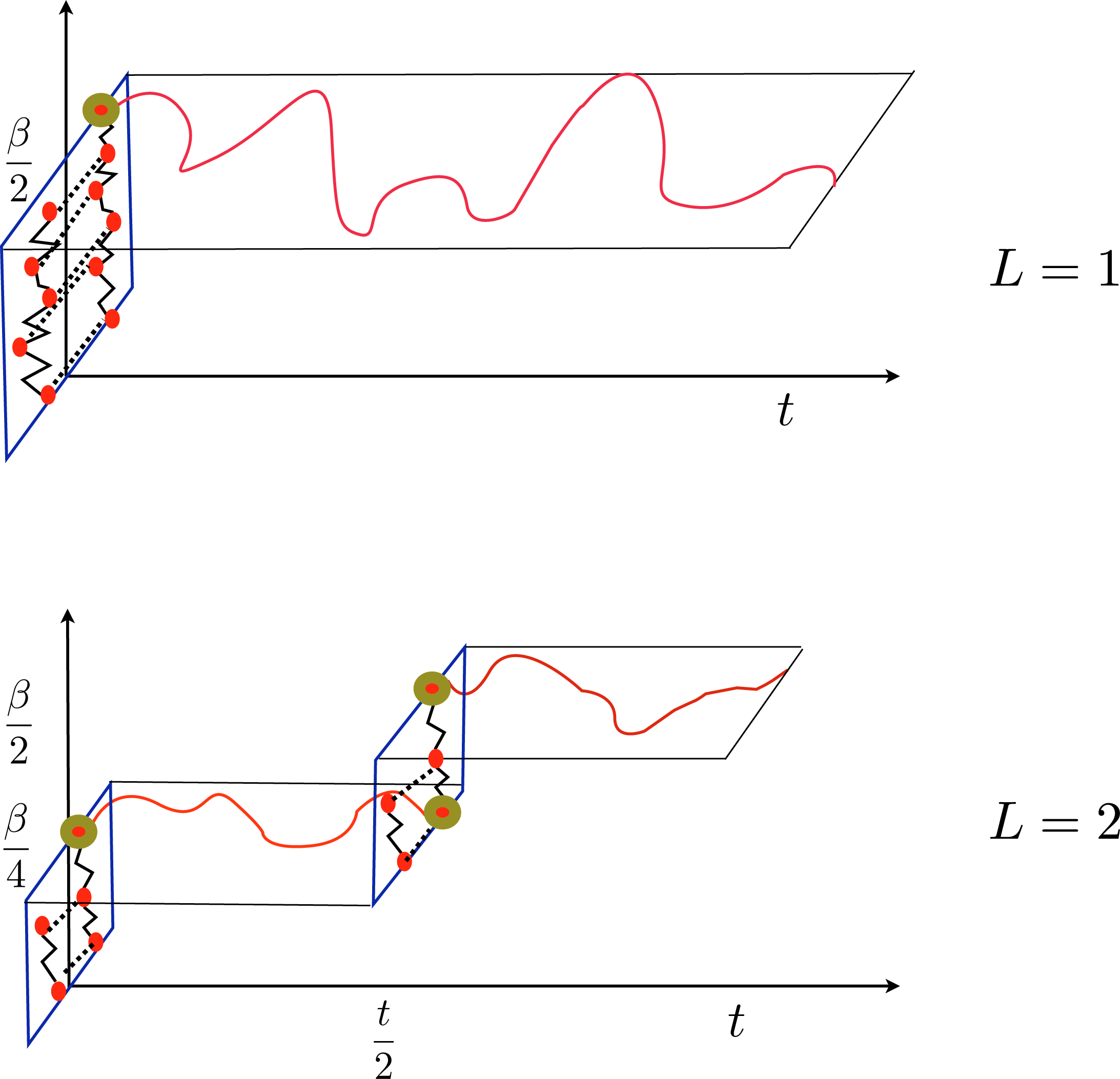
The expression above is interesting. First of all, assuming that the linearization approximation of each short time propagator improves when the propagation time goes to zero, there is potential for systematic improvement with increasing L, and indeed, numerical tests [30] indicate that this is the case. However, the limit for large L, and, in particular, the validity of the expansion in the difference path at the intermediate times of the propagation, is delicate. In fact, while it can be argued that the matrix elements of operators  and B̂ (usually diagonal) force the forward and backward paths (the free and tilde variables in the upper panel of Figure 1) to start and end close to one another, and, therefore, that only small values of the difference among the paths will be relevant close to the initial and final time, truncating the expansion of the difference of the potentials along the whole pair of paths is considerably more delicate. This issue, and the nature of the dynamics when L → ∞, are currently under investigation. In the meantime, note that the ρ functions are positive definite, so that they can be used to define a probability density for sampling the overall path variables (i.e., the full set of {J}J= 0,...,L−1 variables) as , where Ω is the (unknown) normalization factor. The method to deal with this factor is illustrated in the next subsection for the case L = 1 and can be straightforwardly generalized to L > 1. The probability density, Π, corresponds to a stochastic process, which concatenates the thermal and time propagations within each short time propagator, Kl. The structure of the propagations in real and imaginary time is determined by the definition of ρ in Equation (15) and can be described as follows. For L = 1, there is only one real-time leg of duration τt = t, while the imaginary time propagation corresponds to an inverse temperature β/2 for both the semi-sum and difference variables. The upper panel of Figure 3 illustrates these propagations with a sketch. In the figure, the horizontal axis is time and the vertical axis temperature. The vertical plane represents the space of configurations associated with the thermal path integral for both the semi-sum and difference variables; the thermal beads are represented with the red circles. The harmonic interactions in the thermal paths are indicated with zigzagged lines connecting adjacent beads, while the interactions among the two paths due to the potential are drawn as dashed lines. Note that the difference variables path, on the left in the vertical plane in the figure, has one less bead than the semi-sum variables path, due to the integration carried out to isolate a Gaussian probability density for the initial momenta. The propagation in real time is drawn as the curve on the horizontal plane, which represents the phase space of the system. The red and golden circle at t = 0 represents the initial conditions for the time evolution: the initial coordinate coincides with the last bead of the thermal path in the semi-sum variables, while the initial momentum is sampled from the Gaussian mentioned before. A phase factor is associated with the initial point of the classical propagation. The exponent of this phase couples the initial momentum of the trajectory with the last bead of the thermal path in the difference variables. A phase factor is also associated with the final point of the classical propagation, where, for L = 1, the exponent couples the momentum at time t with the variable, Δr1. The integrals over and Δr1 in the expression for involve products of these phase factors with the matrix elements of operators  and B̂. The end-point integral reconstructs the Wigner transform of the operator, B̂. To see this, consider Equation (16). For L = 1, the second line of the equation is absent, and boundary conditions impose Δr1 = Δrtc (with similar relationships for the sum variables). With this notation, the integral over Δrtc is recognizable as the Wigner transform of operator B̂. The structure of the sequence of imaginary and real-time propagation for generic values of L can be inferred from the lower part of Figure 3, where we show what happens for L = 2. In this case, there are two segments of classical dynamics, each of duration t/2, and two propagations of semi-sum and difference variables in imaginary time, taking the system from zero inverse temperature to β/4 and from β/4 to β/2, respectively. As before, the first segment of dynamics starts, with a Gaussian initial momentum, from the last bead of the semi-sum variable thermal path at t = 0. The end-point of this leg of propagation is the initial configuration for the semi-sum variable thermal path at t/2, and the second segment of dynamics has as initial conditions the final coordinate of the semi-sum variable thermal path and a new momentum sampled from a Gaussian. The variances of the Gaussians associated with the momentum sampling are doubled with respect to the case L = 1. The integrand now contains four phase factors coupling the momenta at the beginning and end of each classical dynamics segment with the values of the difference path variables at the end and at the beginning of each thermal slice, respectively. The phase factor that depends on (i.e., the phase factor computed at time t) can again be combined with the matrix element of operator B̂ to obtain the Wigner transform of this operator at the final time of the propagation, so that only three phases remain to contribute to the result. In general, involves L segments of classical propagation, each of duration t/L, interspersed with L pairs of thermal paths in the semi-sum and difference variables, each at an inverse temperature β/2L. The rules for connecting the coordinate and momenta at the initial and final time of the dynamics with the final and initial points of the thermal paths and for constructing the 2L − 1 phase factors contributing to the integrand (the phase factor at time t can always be absorbed in the Wigner transform of operator B̂) are completely analogous to the L = 2 case.
A Monte Carlo algorithm to sample Π for different values of L was illustrated in [30]. This Monte Carlo has several non-standard features, most notably the fact that the normalization of the probability density is unknown and that Π contains products of delta functions, i.e., singular distributions. These difficulties can be circumvented as detailed in [30]. The first one is tackled by recasting (without further approximations) Equation (16) in the form of a ratio of expected values. The second is addressed via an appropriate choice of the trial moves and acceptance probabilities. The most serious numerical difficulty, unfortunately, comes from the estimator of the observable. In fact, from Equation (16), it can be seen that, in addition to the matrix elements of the operators, the integrand contains a product of phase factors to be evaluated at the beginning and end of each real-time propagation segment. As mentioned above, the number of these phase factors for the “order L” approximation of the symmetrized correlation function is 2L − 1, and their presence rapidly hinders the convergence of the calculation. Furthermore, for a system of n particles in three dimensions, the phases take the (generic) form , where p and Δr are 3n-dimensional vectors. The number of phase factors thus scales linearly with the number of degrees of freedom, so that, even for small values of L, convergence is problematic. The numerical tests performed so far on simple model systems confirm both the interest and the difficulties of Equation (16). In [30], we computed position autocorrelation functions for a set of one-dimensional systems (e.g., quartic potential) at temperatures low enough to ensure that the system was in the quantum regime. We observed that increasing the number of complex time slices did systematically improve the length of time for which we were able to get accurate results. However, the numerical effort to go beyond L = 3, though not exponential in time, became essentially prohibitive, even for these simple systems. To indicate possible means to reduce the numerical effort involved in these calculations, we now discuss a recent development of the method developed to address the problem of the phase in the simplest case, L = 1, in which it presents itself. We then illustrate how to formally extend this development, which, in its simplest form, has been successfully applied to realistic models of condensed phase systems, to the case L > 1.
3. L = 1: Fully Linearized Approximation
The expression for the L = 1 approximation of the symmetrized correlation function is given by (see Equation (16)):
We are now going to simplify the expression above using four steps: (1) observe that the integral over Δrtc in the first line of the equation above defines the Wigner transform of operator B̂ (see, also, the definition below Equation (4)); (2) note that the product of δ functions in the definition of ρ (Equation (15)) forces (r̃tc, ) to be endpoints of a classical trajectory of length t starting at ( , ), so that, after integration over r̄(ν+l) (l = 1, ..., n − 1) and p̄l (l = 1, ..., n), (r̄tc, ) = (rt, pt) (where (rt, pt) denote the classically evolved variables); (3) choose, for the sake of simplicity, to specialize the discussion to an operator, Â, which is diagonal in the coordinate representation (the case of generic operators is considered in the Appendix of [39]). This choice, producing a δ(Δr0) in the evaluation of the matrix elements, allows one to integrate also over Δr0. The surviving variables (i.e., the semi-sum and difference variables of the thermal path integral and the initial momentum of the classical trajectory) will be indicated collectively as Γ = {p1, r0, …, rν, Δr1, …, Δrν−1}; (4) simplify the notation by dropping the bar from the semi-sum variables and the subscript, which identifies the J = 0 propagation segment in Equation (16), since only one segment is now present. Once these operations are performed, the correlation function can be written as:
As anticipated, both in the numerator and denominator of this expression, a phase factor appears, which, for high dimensional systems, hinders an efficient convergence of the calculation. To alleviate this problem, we proposed a method, described in detail in [39], which starts by obtaining an alternative expression for . As will be shown in the following, the new expression does not introduce further (analytical) approximations, but it has the advantage of eliminating the phase factor from the observable. Let us consider in more detail the structure of the probability, P(Λ). This probability is given by the product of a Gaussian for the momenta, (note that, with respect to Equation (19), we dropped the superscript, 1, on the momenta to simplify the notation), times a joint probability function for the semi-sum and difference thermal variables to be indicated in the following as ρ̃(r, Δr), where we have introduced the notation r = {r0, …, rν} and Δr = {Δr1, …, Δr(ν−1)}. This joint probability (whose form can be inferred from Equation (19) by taking out the momentum Gaussian) is most conveniently expressed as:
3.1. Noisy Monte Carlo Algorithm
To simplify the discussion, we introduce some notation. Let us indicate the coordinate-dependent Gaussian terms in Equation (19) as:
We also rewrite the marginal probability, ρm(r), defined in Equation (22), isolating the terms that do not depend on Δr and have an explicit analytic expression, thus:
The Monte Carlo scheme to sample Equation (31) is constructed as follows. Choose, with probability 1/2, if the move will involve r or p.
(1) A move on p has been selected:
choose a new momentum according to p′ = p + δp, where δp is a uniform random number centered on zero (the magnitude of the displacement is chosen so as to optimize the acceptance). Taking into account that the r variables are not being updated, detailed balance for this trial move takes the form:
The expression for the acceptance probability differs from the standard Metropolis prescription for the presence of and is valid when [42]. In the limit of an infinitely precise estimate of the difference, and the standard criterion is recovered; when non-zero, this function corrects, on average, for the effect of the noise.
(2) A move on r has been selected:
in this case, indicating with Tr(r → r′) and Ar(r → r′) the probability to generate and accept a new configuration, respectively, detailed balance is expressed, after simplifying ρG(p), as:
The structure of this relationship is analogous to the one considered by Kennedy et al. [43], who adapted Monte Carlo sampling to probability densities given by an exponential term times a “noisy” (positive definite) function. They showed that detailed balance is satisfied if states are generated according to the probability:
Above, (r → r′) is an unbiased estimator of the ratio, , and c < 1 is a constant that ensures Ar(r → r′) ∈ [0, 1] (for details on the meaning and choice of c, see [43] and the discussion on page 8 of [39]). The conditions on the exponential of the potential enforce an ordering criterion on the states, whose optimal choice depends on the problem (here, we used the one adopted in our previous work [39]). In the usual implementation of the Kennedy method, the exponential part of the probability density is assumed to be known analytically, and the states are generated via a standard Monte Carlo method. In our case, the situation is more complicated, since e−E(r′,p) is only known with noise. To solve this problem, we employ the penalty method to obtain configurations distributed according to Equation (36). These configurations are generated using a Monte Carlo with transition probability t(r → r′) ∝ e−Vr(r′) and acceptance probability where Δr(r′,r; p) is an unbiased estimator of E(r′, p) − E(r, p), and is defined in analogy with Equation (34).
This concludes the description of our Monte Carlo moves. The practical implementation of this algorithm requires the definition of the numerical estimators, (r → r′), Δp(p′, p; r) and Δr(r′, r; p). While this is an important technical point, it only involves a set of calculations, each performed via an auxiliary Monte Carlo move, that are quite standard. To provide a typical example, we consider one of the estimators referring the reader to [39] for a detailed description of the others. Let us then consider (r → r′). This quantity, necessary in the Kennedy acceptance test, see Equation (37), is obtained by writing the ratio of the marginal probabilities as:
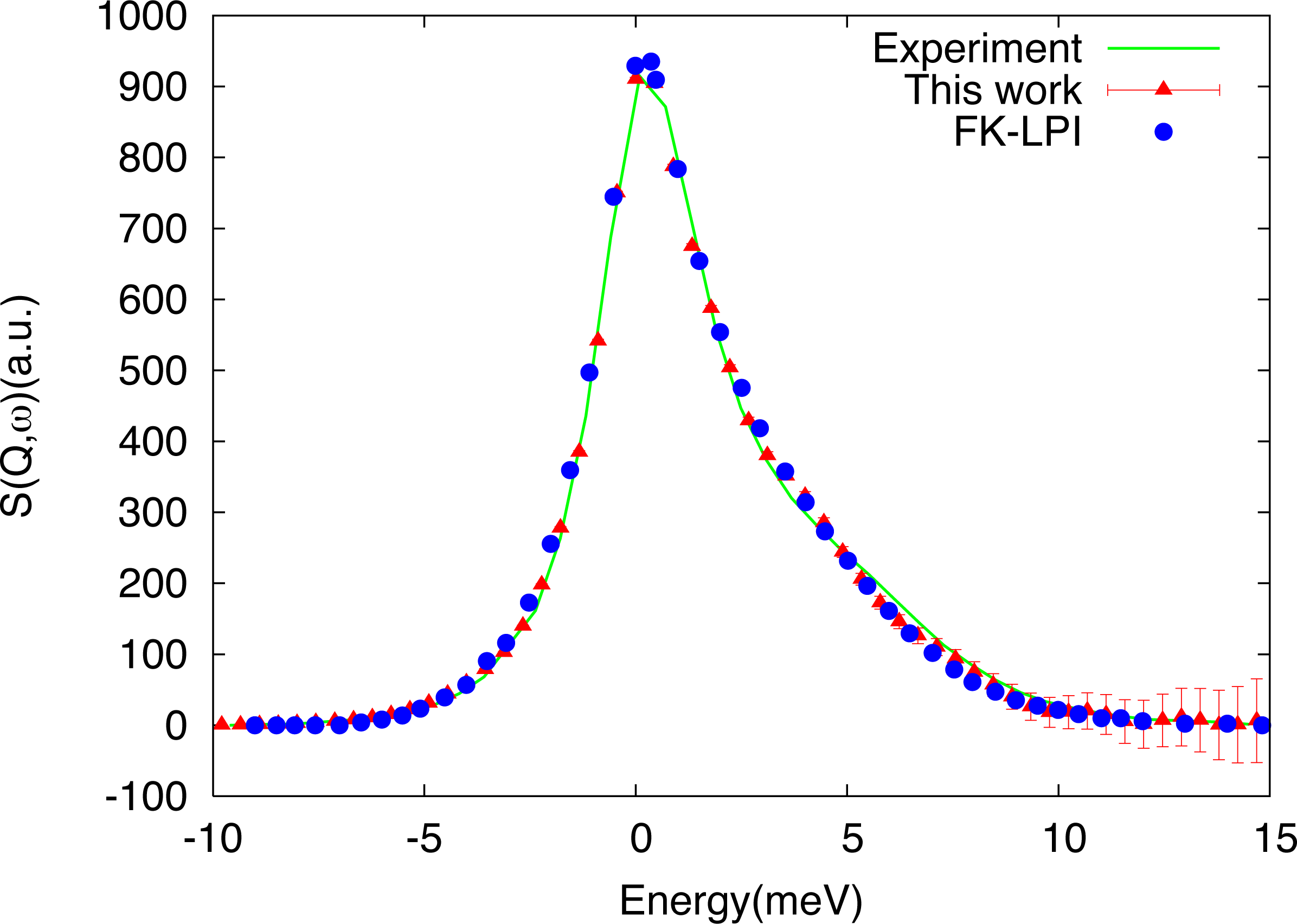
The computational overhead introduced by the auxiliary Monte Carlo calculation increases the cost of our calculation, but it is very small compared to the number of moves necessary to converge the estimate of Equation (20). The algorithm just described is, in fact, efficient enough to make possible calculations on realistic condensed phase systems with relatively little numerical effort. In particular, the algorithm was used to compute the dynamic structure factor of a model of liquid neon composed of 64 atoms [38]. Details of the calculation can be found in [38]. Here, we show, in Figure 4, our results (red triangles with error bars in the figure) and compare them with experiments (green curve) and the results of a calculation (with the same empirical potential and simulation parameters) performed by Poulsen et al. [45] using the linearized approximation for quantum time correlation functions described in the Introduction (see Equation (4) and the discussion above it).
The results show a rather pronounced asymmetry around zero, due to detailed balance, that indicates the presence of relevant quantum effects in the system. The agreement between our calculations and experiments is very good, as it is the agreement with the standard linearized calculation by Poulsen (a state-of-the-art reference in the field). The numerical cost of the two calculations is very similar (about a million Monte Carlo steps in total for initial condition sampling), showing that the auxiliary steps, due to the noisy distributions in our approach, are essentially irrelevant. Indeed, other tests indicate that, depending on the system, the overall cost of our method can be less than that of alternative schemes with comparable or better accuracy. The approach described in this section, for example, has also been used to obtain the infrared spectra of simple models of molecules in the gas phase [46]. Although these systems are quite small, the calculations that we performed are known to pose a considerable challenge to alternative, less rigorous methods, such as Centroid Molecular Dynamics [47] and Ring Polymer Molecular Dynamics [48], which fail to capture the spectra and/or introduce spurious features. In contrast, even though obtaining the exact intensities is quite expensive, our method proved remarkably effective in identifying the positions of the peaks, which could be obtained with only about one hundred Monte Carlo moves.
3.2. L > 1
In this subsection, we present a new development of the approach summarized above that extends the use of cumulants to pre-average the phase factors in the expression of the symmetrized correlation function to the case L > 1 (This possibility came out in discussions with M. Monteferrante.). For simplicity of notation, in this subsection, we describe how this can be done for L = 2, but the steps that we shall use can be generalized to a larger number of segments. In the following, we report the formal result, while the construction and test of an algorithm that generalizes the noisy Monte Carlo scheme described in the previous section will be the object of future work. Let us begin by rewriting the L = 2 approximation of the symmetrized correlation function, for diagonal Â, as follows (see Equations (16) and (20) for structure and notation):
In the equation above, ( ) is the endpoint of the propagation obtained by combining the two segments of classical dynamics described in the lower panel of Figure 3; and indicate the variables associated with the first and second set of thermal path integrals, respectively (the first set does not include , since this variable can be integrated over for diagonal Â, and the second does not include , since this is the endpoint of the, deterministic, classical propagation from zero to t/2 in Figure 3). P(Γ0) was defined in the previous section (see Equation (19)), and:
For J = 0, the definition above is to be read as identical to Equation (24). For J = 1 (and, in general, J > 0), λ = {λ1, λ2} is a vector of positive integers (including zero), |λ| is their sum, λ! = λ1! λ2! and:
As in the previous subsection, the conditional distribution density is even with respect to the difference variables, implying that only even terms are non-zero in Equation (43). The function F (πJ, rJ) is then real and positive, so we can set F (πJ, rJ) = e−E(πJ,rJ) and define, in analogy with Equation (26), the probability density:
Substitution of the definition above in the expression for the symmetrized correlation function shows that we can write the two-segment approximation as the following expectation value:
4. Conclusions
In this paper, we summarized a recently developed method to approximate symmetrized quantum time correlation functions. The method recasts the problem as the calculation of averages over a stochastic process based on a linearized approximation of the complex time propagators in the correlation function. This approximation can be enforced either on the full length of the evolution (fully linearized approach) or in an iterative form obtained via the (complex) time composition property of the evolution operators. Thanks to the use of a cumulant expansion, which tames the phase factors present in the observable, the fully linearized approach has proven efficient and accurate in calculations on moderately quantum systems in the condensed phase. The iterative form offers, in principle, a way to improve the accuracy of the results with respect to the fully linearized case and may be useful when higher order quantum effects must be kept into account. While the potential for systematic improvement with respect to the fully classical limit for the dynamics is indeed the most interesting feature of the approach (and the one that distinguishes it from other available methods for which there is no way to improve upon the classical or semi-classical approximation), the practical use of the approach for L > 1 is currently hindered by numerical instabilities. In the final section of the paper, we have shown how to extend the use of the cumulant expansion to obtain a formal expression for this case that does not require one to average phase factors in the observable. This expression may be a promising starting point for considerable improvement of the algorithm for more than one segment, and future work will focus on developing and testing an appropriate algorithm. However, importantly, while numerical evidence on model systems supports the claim that systematic improvements can be obtained by higher order iterations, an exact statement on the convergence properties of the method is lacking, and further investigation is needed to formally assess the features of the scheme.
Acknowledgments
The authors are grateful to C. Pierleoni and M. Monteferrante for their substantial contributions to the earlier methods for symmetrized correlation functions summarized in this work. Funding from IIT-SEED grant No 259 “SIMBEDD” is also acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Feynman, R. Space-time approach to non-relativistic quantum mechanics. Rev. Mod. Phys 1948, 20, 367–387. [Google Scholar]
- Schulman, L.S. Techniques and Applications of Path Integration; Dover Publications: Dover, UK, 2005; p. 448. [Google Scholar]
- Van Vleck, V. The correspondence principle in the statistical interpretation of quantum mechanics. Proc. Natl. Acad. Sci. USA 1928, 14, 178–188. [Google Scholar]
- Miller, W.H. Classical S matrix: Numerical application to inelastic collisions. J. Chem. Phys 1970, 53, 3578. [Google Scholar]
- Miller, W.H. The semi-classical initial value representation: a potentially practical way for adding quantum effects to classical molecular dynamics simulations. J. Phys. Chem. A 2001, 105, 2942–2955. [Google Scholar]
- Kleinert, H. Path Integrals in Quantum Mechanics, Statistics, and Polymer Physics, and Financial Markets; World Scientific: River Edge, New Jersey, USA, 2004. [Google Scholar]
- Glauber, R. Quantum theory of optical coherence. Phys. Rev 1963, 1449, 2529–2539. [Google Scholar]
- Kay, K.G. Integral expressions for the semiclassical time-dependent propagator. J. Chem. Phys 1994, 100, 4377. [Google Scholar]
- Caratzoulas, S.; Pechukas, P. Phase space path integrals in Monte Carlo quantum dynamics. J. Chem. Phys 1996, 104, 6265. [Google Scholar]
- Herman, M.F.; Kluk, E. A semiclassical justification for the use of non-spreading wavepackets in dynamics calculations. Chem. Phys 1984, 91, 27–34. [Google Scholar]
- Kluk, E.; Herman, M.F.; Davis, H.L. Comparison of the propagation of semiclassical frozen Gaussian wave functions with quantum propagation for a highly excited anharmonic oscillator. J. Chem. Phys 1986, 84, 326. [Google Scholar]
- Ankerhold, J.; Pollak, E.; Kay, K.G. The Herman Kluk approximation: Derivation and semiclassical corrections. Chem. Phys 2006, 322, 3–12. [Google Scholar]
- Shao, J.; Makri, N. Forward-Backward semiclassical dynamics with linear scaling. J. Phys. Chem. A 1999, 103, 9479. [Google Scholar]
- Herman, M.F.; Coker, D.F. Classical mechanics and the spreading of localized wave packets in condensed phase molecular systems. J. Chem. Phys 111.
- Hernandez, R.; Voth, G.A. Quantum time correlation functions and classical coherence. Chem. Phys 1998, 233, 243–255. [Google Scholar]
- Poulsen, J.A.; Nyman, G.; Rossky, P.J. Practical evaluation of condensed phase quantum correlation functions: A FeynmanKleinert variational linearized path integral method. J. Chem. Phys 2003, 119, 12179. [Google Scholar]
- Shi, Q.; Geva, E. A relationship between semiclassical and centroid correlation functions. J. Chem. Phys 2003, 118, 8173. [Google Scholar]
- Poulsen, J.A.; Nyman, G.; Rossky, P.J. Static and dynamic quantum effects in molecular liquids: A linearized path integral description of water. Proc. Natl. Acad. Sci. USA 2005, 102, 6709–6714. [Google Scholar]
- Wigner, E. On the quantum correction for thermodynamic equilibrium. Phys. Rev 1932, 40, 749–759. [Google Scholar]
- Tully, J.C. Trajectory surface hopping approach to nonadiabatic molecular collisions: The reaction of H+ with D2. J. Chem. Phys 1971, 55, 562. [Google Scholar]
- Kapral, R.; Ciccotti, G. Mixed quantum classical dynamics. J. Chem. Phys 1999, 110, 8919. [Google Scholar]
- Kapral, R. Progressin the theory of mixed quantum classical dynamics. Annu. Rev. Phys. Chem 2006, 57, 129–157. [Google Scholar]
- Bonella, S.; Coker, D.F. LAND-map, a linearized approach to nonadiabatic dynamics using the mapping formalism. J. Chem. Phys 2005, 122, 194102. [Google Scholar]
- Bonella, S.; Montemayor, D.; Coker, D.F. Linearized path integral approach for calculating nonadiabatic time correlation functions. Proc. Natl. Acad. Sci. USA 2005, 102, 6715–6719. [Google Scholar]
- MacKernan, D.; Ciccotti, G.; Kapral, R. Trotter-based simulation of quantum classical dynamics. J. Phys. Chem. B 2008, 112, 424–432. [Google Scholar]
- Kim, H.; Nassimi, A.; Kapral, R. Quantum classical Liouville dynamics in the mapping basis. J. Chem. Phys 2008, 129, 084102. [Google Scholar]
- Nassimi, A.; Kapral, R. Mapping Approach for Quantum Classical Time Correlation Functions. Can. J. Chem 2009, 87, 880–890. [Google Scholar]
- Nielsen, S.; Kapral, R.; Ciccotti, G. Statistical mechanics of quantum classical systems. J. Chem. Phys 2001, 115, 5805. [Google Scholar]
- Agostini, F.; Caprara, S.; Ciccotti, G. Do we have a consistent non adiabatic quantum classical mechanics? Europhys. Lett 2007, 78, 30001. [Google Scholar]
- Bonella, S.; Monteferrante, M.; Pierleoni, C.; Ciccotti, G. Path integral based calculations of symmetrized time correlation functions. II. J. Chem. Phys 2010, 133, 164105. [Google Scholar]
- Schofield, P. Space-time correlation function formalism for slow neutron scattering. Phys. Rev. Lett 1960, 4, 239–240. [Google Scholar]
- Filinov, V. Wigner approach to quantum statistical mechanics and quantum generalization molecular dynamics methods. Part 1. Mol. Phys 1996, 88, 1517. [Google Scholar]
- Filinov, V. Wigner approach to quantum statistical mechanics and quantum generalization molecular dynamics method. Part 2. Mol. Phys 1996, 88, 1529. [Google Scholar]
- Miller, W.H.; Schwartz, S.D.; Tromp, J.W. Quantum mechanical rate constants for bimolecular reactions. J. Chem. Phys 1983, 79, 4889. [Google Scholar]
- Frantsuzov, P.A.; Mandelshtam, V.A. Quantum statistical mechanics with Gaussians: Equilibrium properties of van der Waals clusters. J. Chem. Phys 2004, 121, 9247–9256. [Google Scholar]
- Jadhao, V.; Makri, N. Iterative Monte Carlo for quantum dynamics. J. Chem. Phys 2008, 129, 161102. [Google Scholar]
- Bonella, S.; Monteferrante, M.; Pierleoni, C.; Ciccotti, G. Path integral based calculations of symmetrized time correlation functions. I. J. Chem. Phys 2010, 133, 164104. [Google Scholar]
- Monteferrante, M.; Bonella, S.; Ciccotti, G. Quantum dynamical structure factor of liquid neon via a quasiclassical symmetrized method. J. Chem. Phys 2013, 138, 054118. [Google Scholar]
- Monteferrante, M.; Bonella, S.; Ciccotti, G. Linearized symmetrized quantum time correlation functions calculation via phase pre-averaging. Mol. Phys 2011, 109, 3015–3027. [Google Scholar]
- Lindley, D.V. Introduction to Probability and Statistics from a Bayesian Viewpoint, Part 1, Probability; Cambridge University Press: Cambridge, UK, 1965. [Google Scholar]
- Causo, M.S.; Ciccotti, G.; Bonella, S.; Vuilleumier, R. An adiabatic linearized path integral approach for quantum time-correlation functions II: A cumulant expansion method for improving convergence. J. Phys. Chem. B 2006, 110, 16026–16034. [Google Scholar]
- Ceperley, D.M.; Dewing, M. The penalty method for random walks with uncertain energies. J. Chem. Phys 1999, 110, 9812. [Google Scholar]
- Kennedy, A.; Kuti, J. Noise without noise: A new Monte Carlo method. Phys. Rev. Lett 1985, 54, 2473–2476. [Google Scholar]
- Sprik, M.; Klein, M.; Chandler, D. Staging: A sampling technique for the Monte Carlo evaluation of path integrals. J. Chem. Phys 1985, 31. [Google Scholar]
- Poulsen, J.; Scheers, J.; Nyman, G.; Rossky, P. Quantum density fluctuations in liquid neon from linearized path-integral calculations. Phys. Rev. B 2007, 75, 1–5. [Google Scholar]
- Beutier, J.; Bonella, S.; Monteferrante, M.; Vuilleumier, R.; Ciccotti, G. Gas Phase Infrared Spectra via the Phase Integration Quasi Classical Method. Mol. Phys. 2013. accepted. [Google Scholar]
- Cao, J.; Voth, G.A. A new perspective on quantum time correlation functions. J. Chem. Phys 1993, 99, 10070. [Google Scholar]
- Craig, I.R.; Manolopoulos, D.E. Quantum statistics and classical mechanics: Real time correlation functions from ring polymer molecular dynamics. J. Chem. Phys 2004, 121, 3368–3373. [Google Scholar]

© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Bonella, S.; Ciccotti, G. Approximating Time-Dependent Quantum Statistical Properties. Entropy 2014, 16, 86-109. https://doi.org/10.3390/e16010086
Bonella S, Ciccotti G. Approximating Time-Dependent Quantum Statistical Properties. Entropy. 2014; 16(1):86-109. https://doi.org/10.3390/e16010086
Chicago/Turabian StyleBonella, Sara, and Giovanni Ciccotti. 2014. "Approximating Time-Dependent Quantum Statistical Properties" Entropy 16, no. 1: 86-109. https://doi.org/10.3390/e16010086




