Multiscale Model Selection for High-Frequency Financial Data of a Large Tick Stock by Means of the Jensen–Shannon Metric
Abstract
: Modeling financial time series at different time scales is still an open challenge. The choice of a suitable indicator quantifying the distance between the model and the data is therefore of fundamental importance for selecting models. In this paper, we propose a multiscale model selection method based on the Jensen–Shannon distance in order to select the model that is able to better reproduce the distribution of price changes at different time scales. Specifically, we consider the problem of modeling the ultra high frequency dynamics of an asset with a large tick-to-price ratio. We study the price process at different time scales and compute the Jensen–Shannon distance between the original dataset and different models, showing that the coupling between spread and returns is important to model return distribution at different time scales of observation, ranging from the scale of single transactions to the daily time scale.1. Introduction
The complexity of market behavior has fascinated physicists and mathematicians for many years [1]. One of the main sources of interest comes from the difficulty of modeling the rich dynamics of asset prices. In fact, since the beginning of the last century, a large set of statistical regularities of price dynamics has been identified, including the asymptotically power-law distribution of returns, their lack of linear correlations, but the presence of very persistent higher order correlations, the slow convergence to the Gaussian distribution, scaling properties, multifractality, etc.[2–4]. The modeling activity has been correspondingly very intense, considering models both in discrete and in continuous time, and including random walks, Levy processes, stochastic volatility models, multifractal models, etc.[1,5–8]. However, up to now, there is no consensus on a model that is able to reproduce all the statistical regularities, and therefore, there is a growing interest toward methods allowing one to discriminate among different models those more suited to describe financial data.
A specific challenge is the modeling of how the return distribution changes at different time scales [3]. Due to the presence of fat-tailed distributions, also at very short time scales, and non-linear time correlations, the dynamics of the price-change distribution is far from trivial and not well described by any model. The problem becomes even more dramatic when one wants to describe the price-change distribution also at the shortest time scales, i.e., when the discrete nature of trading appears. Trading and, correspondingly, price changes occur at discrete time. Moreover, an asset price cannot assume arbitrary values, but it is constrained to live in a grid of values fixed by the exchange. The tick size is the smallest interval between two prices, i.e., the grid step. Since tick size can be a sizable fraction of the asset price, when seen at small time scales, price movement appears as a (non-trivial) random walk on a grid, with jumps occurring at random times, while at large time scales, one can probably forget the microstructural issues and describe the dynamics with a more traditional stochastic differential equation or time series approach. One of the main methodological problem is, therefore, to have a method to compare data and model predictions at different time scales.
In this work, we propose to perform multiscale model selection for financial time series by using the Jensen–Shannon distance [9–11], and we specifically consider the case of models describing the high frequency dynamics of large tick assets, i.e., assets where the ratio between tick and price is relatively large [12,13]. We perform the model selection at different scales m, representing the level of aggregation of the time series. In other words, given the return time series, x(t), we study the properties of the probability distribution of its sums . It is important to clarify that we do not perform a goodness-of-fit test at different scales m defining a p-value relative to a specific statistic, e.g., Kolmogorov–Smirnov statistic, etc.[14]. Our analysis consists, instead, in the comparison between the probability distribution computed from empirical data and those computed from synthetic data generated by specific statistical models. The discrepancy is measured by the Jensen–Shannon distance. In particular, by considering a class of models recently proposed [15], we show that models containing the coupling between price and spread, as well as the time correlation of spread outperform other models without these characteristics in describing the change of the shape of the return distribution across scales.
The paper is organized as follows. In Section 2, we illustrate the definitions of the Jensen–Shannon divergence and distance, and we characterize the unavoidable bias, due to the finiteness of the data sample. In Section 3, we illustrate the statistical models of mid-price and spreads dynamics developed in [15]. Moreover, we apply the Jensen–Shannon distance criteria to select among three competing models of the dynamics of the price of a large tick asset, namely Microsoft. Finally in Section 4, conclusions and perspectives are discussed.
2. Jensen–Shannon Distance
Distance or divergence measures are of key importance in a number of theoretical and applied statistical inference and data processing problems, such as estimation, detection, compression and model selection [16]. Among the proposed measures, one of the best known is the Kullback–Leibler (KL) divergence between two distributions, D (p‖q) [17], also called relative entropy. It is a measure of the inefficiency of assuming that the distribution is q when the true distribution is p. It is used in many different applications, such as econometrics [18], clustering analysis [19], multivariate analysis [20,21], neuroscience [22] and discrete systems [23]. We will limit the following discussion to discrete probability distributions, but the results can be generalized to probability density functions.
Let X be a discrete random variable with support of definition and probability mass function p (x), x ∈ . If q (x) is another probability mass function defined on the same support, , the KL-divergence is defined as:
In this paper, we are interested in using the Jensen–Shannon distance as a method for selecting among a set of models the one that best describes a given dataset. We are concerned with the case when our data is represented by a discrete time series of length N. When considering different competing models, we search for the best model describing the probability distribution of the aggregation (i.e., sum) of the time series at different time scales m. Moreover, the use of Jensen–Shannon distance allows us to compare two empirical distributions.
To be more specific, consider the random variable, x, taking values from the set x = (x1, ⋯, xk) with probabilities p = (p1, ⋯, pk).Given N observations of the time series, x(t), t = 1, .., N, one builds a histogram n = (n1, ⋯, nk), where ni is the number of times the outcome was xi. The frequency vector f = (f1, ⋯, fk) = (n1/N, ⋯, nk/N) is an estimator of the probability distribution, p. We want to perform a statistical analysis at different scales of aggregation, i.e., we study the probability distribution, pm, and frequency distribution, fm, of the sum , where the value, m, defines the scale. The probability distribution of the elementary process x(t), corresponding to m = 1, is denoted by pm= 1 = p. If the initial dataset had N values, the scale, m, is limited by 1 ≤ m ≤ N. The number of experimental data available at each aggregation scale m reduces to Nm ≡ ⌊N/m⌋, because we sum the experimental data, which belong to the Nm non-overlapping windows of length m.
In order to select the best model that describes the data at all aggregation scales, we compute the Jensen–Shannon distances for various values of m, i.e., JS (pm, fm). We estimate pm according to different statistical models, and we select the one that minimizes JS (pm, fm) for the different values of m. As will be clear below, we will also need to compute the distance between two frequency distributions in order to compare the two different datasets, JS (f1,m, f2,m). In this case, we assume that the length of the two datasets is the same N1 = N2 = N.
It is important to stress that even if we knew the true distribution, pm, the distance, JS (pm, fm), inferred from a finite sample of data, would be larger than zero. The fluctuations of fm from dataset to dataset may not only result in fluctuations of the numerical values of JS, but also in a systematic shift, i.e., bias, of the numerical values of JS. This bias is identified with the expectation value, E [JS (pm, fm)] ≠ 0, for the various values of the scale, m. The bias is also present if we compute the distance, JS (f1,m, f2,m), between two frequency vectors that are computed from datasets representing the same stochastic process.
The concept of a systematic bias of the numerical values of Jensen–Shannon divergence, DivJS, is well known in the literature, and it is connected to the systematic bias in the estimation of entropy. It follows directly from Jensen inequality [17] that the expected value, E [H (f)], of the entropy computed from an ensemble of finite-length sequences cannot be greater than the theoretical value, H (p), of the entropy computed from the (unobservable) probabilities:
Grosse et al. [37] derived an analytical approximation of the expected value of DivJS (f1, f2) between two i.i.d. sequences of length N coming from the same probability distribution, which is:
2.1. A Simple Binomial Model
In this section, we present a toy example of the use of Jensen–Shannon distance for model selection. The purpose of the section is mostly didactical and serves to show the multiscale procedure and the issues related to the finiteness of the sample that will be present also in the real financial case described in the next section.
Let us consider a process, which at scale m = 1 is a binomial i.i.d. process, i.e., pm= 1 is described by B (n, pB), where pB describes the probability of success. The sum of m i.i.d. binomial variables is still described by a binomial distribution [38], i.e., pm = (pm,1, ⋯, pm,k) is described by B (nm, pB), and its support is a set composed by k = nm + 1 elements. Given a time series of length N, at each aggregation scale, m, we have Nm ≡ ⌊N/m⌋observations from non-overlapping windows, and we measure the frequency vector fm = (nm,1/Nm, ⋯, nm,k/Nm), where nm,i is the number of occurrences of the event, i, at scale m.
The probability distribution of empirical frequencies is given by the multinomial distribution:
In principle, one can compute exactly the moments of the distances, JS (pm, fm) and , which are:
The computational problem with these expectations are the values of k = nm + 1 and of N, because the number of categories of the multinomial distribution grows dramatically with the scale, m. The support of the multinomial distribution for the scale, m, has a number of elements:
To handle this problem, we compute these expectations by means of Monte Carlo simulations, and we replace ensemble averages with sample averages, i.e., for example:
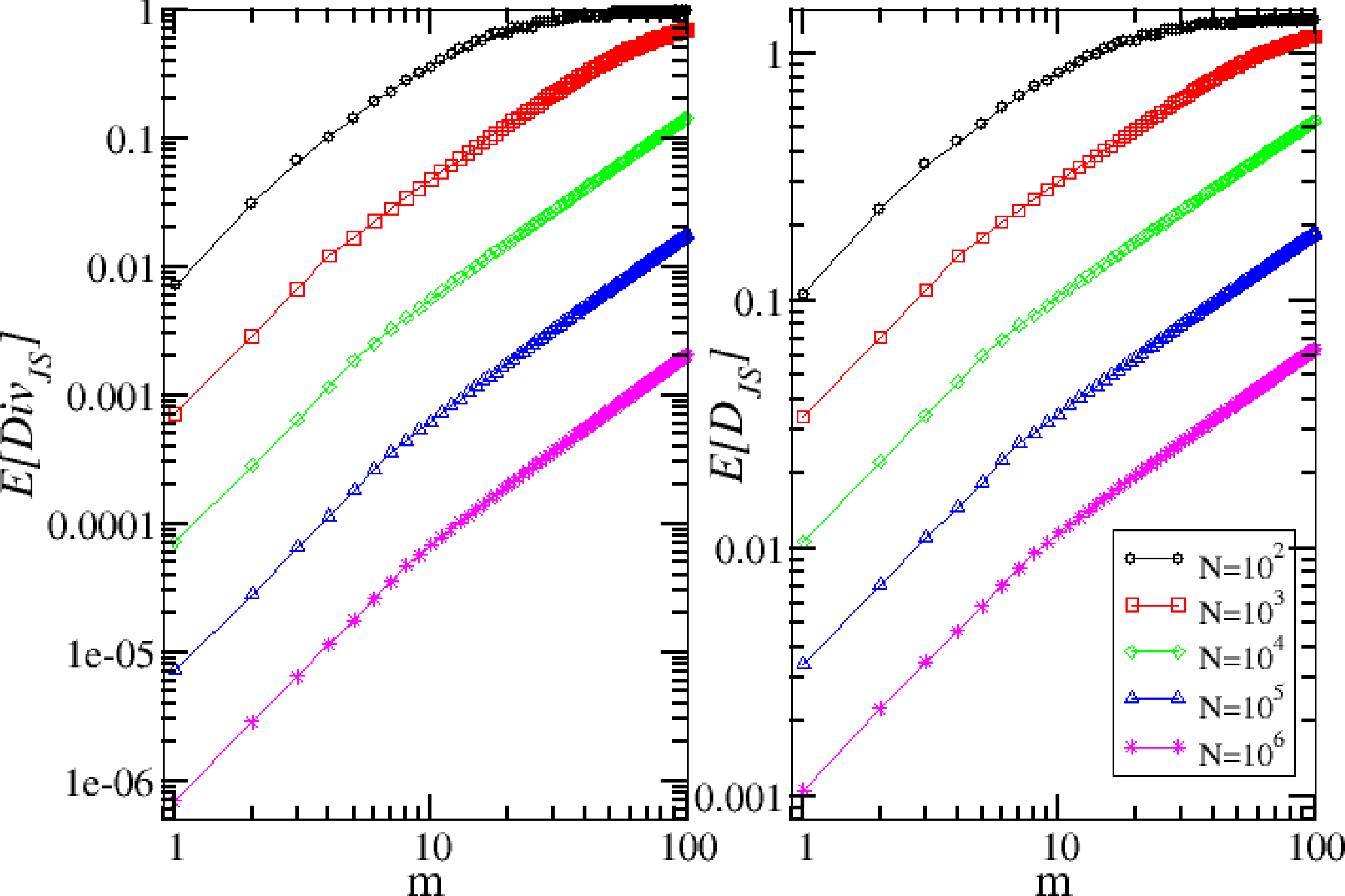
We first consider the problem of the finite sample bias in the computation of the Jensen–Shannon divergence and distance. Specifically, we compute and as a function of the time series length, N, when the two frequency vectors are taken by two independent realizations of the same binomial model. We study the two information functionals in the range m = [1, ⋯, 100] for the values N = 102, 103, 104, 105, 106, as reported in Figure 1.
As expected, the bias decreases with N and increases with m. By using the result in Equation (8) for sequences of i.i.d observations, we are able to compute analytically the shape of the initial part of the curve corresponding to the Jensen–Shannon divergence. In fact, in our framework, we should perform the following substitutions in Equation (8), N → N/m and k → nm + 1, and we thus obtain that the scaling of the Jensen–Shannon divergence as a function of N and m for the binomial model is:
In the case of the Jensen–Shannon distance, we do not have any analytic result and limit ourselves to a power-law fit of the initial part of the curve. For the case N = 106, the fit gives c = (1.1 ± 0.1) × 10−3, e = (1.0 ± 0.1). The initial part of the curve appears to scale linearly with scale m, i.e., .
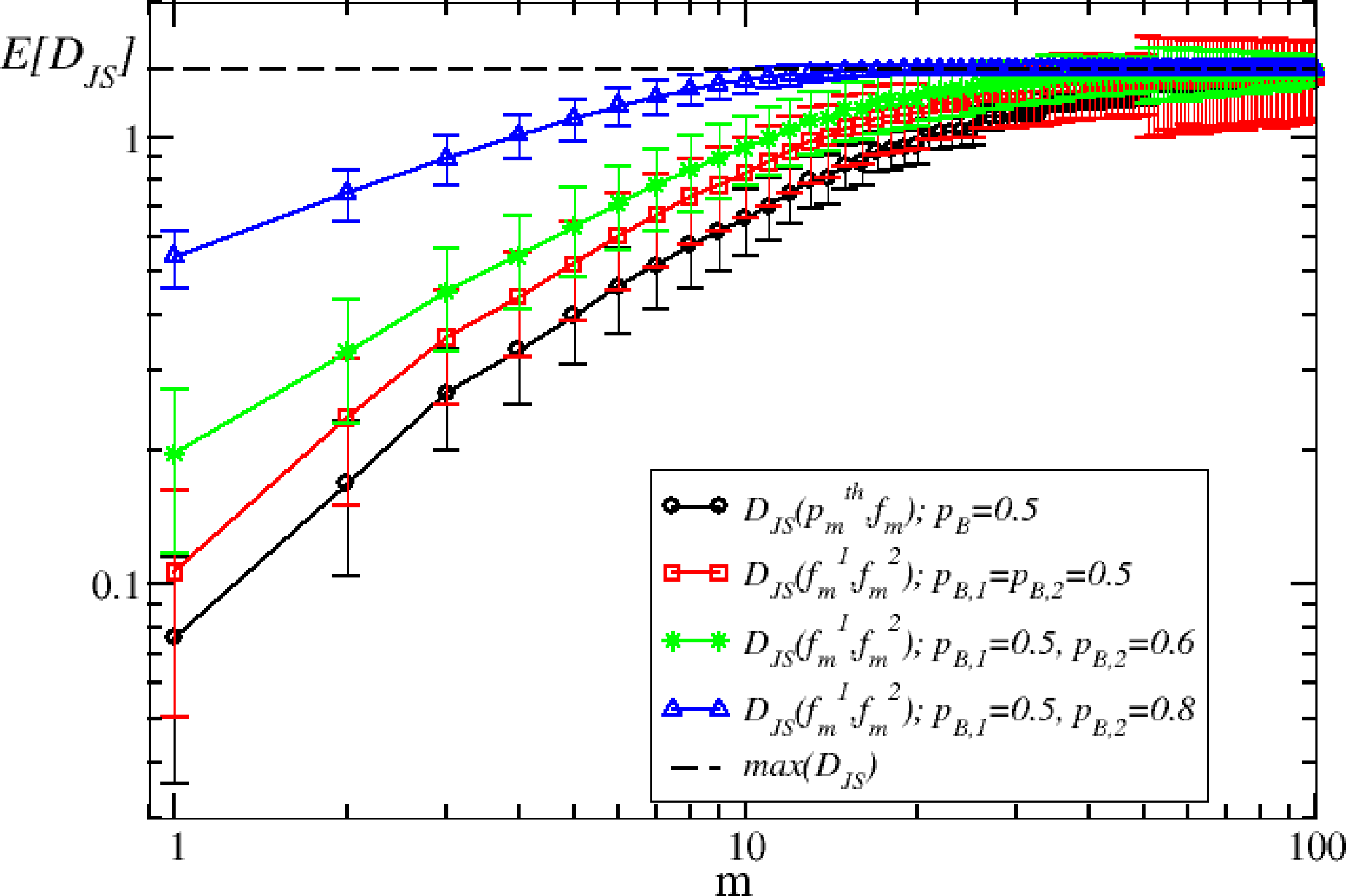
In order to illustrate how to perform model selection with the Jensen–Shannon distance, we consider the case of an (artificial) sample generated from the binomial model with pB = 0.5. We then compare the Jensen–Shannon distance between this sample and another realization of the model with the same parameter and of a realization of the model with different parameter pB ≠ 0.5. As expected, Figure 2 shows that the expected value of the Jensen–Shannon distance between two samples generated by the model with the same parameter is always smaller than the distance between two samples with a different parameter. Moreover, the distance between a sample and the true probability distribution is smaller than the distance between two samples of the same model. This simple observation suggests to us a procedure for selecting models by using the Jensen–Shannon distance.
Specifically, suppose that represents the frequency vector computed from the sample of length N, but we do not known the true model that generates it. Suppose we have a statistical model, from which we are able to simulate an output of the same length. In this case, we can compute a frequency, , from our reference model. To compare the two processes at different scales m, we compute the frequencies, and , from the sums of the initial sample over ⌊N/m⌋ non-overlapping windows. If we have different competing models M1, M2, ⋯, we generate synthetic samples of length N and compute the distances , where the index, l, runs on the possible different models. The model that minimizes the Jensen–Shannon distance at different scales m is the model that reproduces the data better. It is clear that even if we had the true model, the minimum distance at different scales will be different from zero. This is because, as we have seen before, is larger than zero, even when the two samples come from the real model. As we will see in the financial case in the next section, one can split the real sample into two subsamples of length N/2 and compute their Jensen–Shannon distance, to be used as a reference line with respect to the Jensen–Shannon distance between the data and the models.
3. Application to High Frequency Financial Data
In this section, we use the above multiscale procedure, based on the Jensen–Shannon distance, in order to select the best statistical model in the particular case of models describing the high frequency price dynamics of a large tick asset. The models used here were introduced by Curato and Lillo [15], and data refer to NASDAQ (National Association of Securities Dealers Automated) stocks at the time scale of single transactions, traded during July and August, 2009 (see [15] for more details).
3.1. Bid-Ask Spread and Price Dynamics
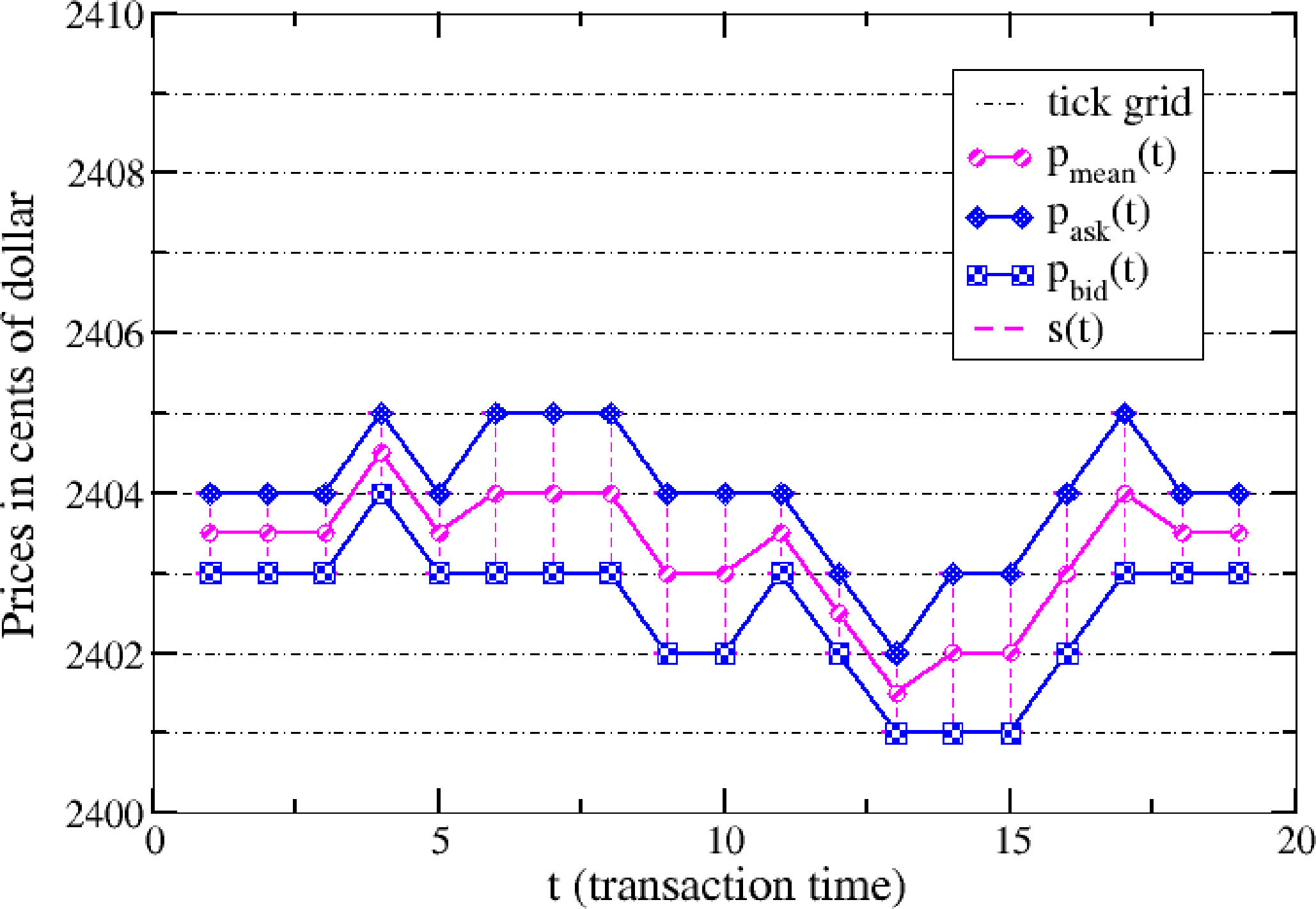
In financial markets, there are two important prices at each time t: the ask price, pASK (t), and the bid price, pBID (t). A customer that wants to buy (sell) a certain volume of the stock submits a buy (sell) market order, which is executed at the ask (bid) price, pASK (pBID). From these two prices, we define the mid-price pmean (t) = (pASK (t) + pBID (t)) /2. Our models are defined in transaction time, which is an integer counter of events defined by the execution of a market order, i.e., t ∈ ℕ. Note that if a market order is executed against several limit orders, our clock advances only by one unit. The price of the order cannot assume arbitrary values, but it can be placed on a grid of fixed values determined by the exchange. The grid step is defined by the tick size, and it is measured in the currency of the asset. The presence of a finite tick size implies that the bid and ask prices can be represented by integer numbers, i.e., pASK, pBID ∈ ℕ, for which the unit is represented by the tick size. Our models are defined by the dynamics of two stochastic variables, i.e., mid-price changes x (t, m) between m consecutive transactions and the bid-ask spread, s (t):
3.2. Markov Dynamics
We compare three different models for price dynamics in transaction time proposed in [15]. The first model, called M0 model, is defined by price changes x (t) that are independent from the spread process, s (t). Instead, in the other two models, i.e., the MS and MSB models, there is a coupling between the process of price changes, x (t), and the spread process, s (t). We now define the price-change processes relative to the time scale m = 1, setting x (t) = x (t, m = 1).
M0 model. The model is defined by an i.i.d process for x (t), where the unconditional distribution, p (x (t)), reproduces the empirical distribution of price changes. In this case, p (x (t) |s (t)) = p (x (t)), i.e., we have independence between the two variables, x and s.
MS model. This model is defined by a particular coupling between the price changes and spread dynamics. We start from the description of the spread process, s (t), because this process will be independent from the process, x (t), whereas x (t) will be the dependent variable.
It is well known that the spread process, s (t), is autocorrelated in time [39,40]. In our models, the spread process, s (t), is represented by a stationary Markov(1) process:
MSB model. This model is a limit case of the MS model. In this case, the spread process is an i.i.d Bernoulli process defined by P (s (t) = 1) = pB. Though s (t) is an i.i.d process, zB (t) is a Markov(1) process defined by:
For the next section, it is useful to quantify the number of possible states of the variables, x (t, m), for different scales m. For our models, the number of states grows linearly with m, i.e., k = 1 + 4m.We stress that we do not have analytic expressions of probability distributions for the process, x (t, m > 1). This is due to the fact that the model is relatively complicated, also because it is correlated in time and, therefore, not i.i.d.. For scales m > 1, we study our models only by Monte Carlo simulations, i.e., we generate a sample of N observations of the processes defined at scales m = 1, and then, we study the properties of on non-overlapping windows of length m.
3.3. Multiscale Model Selection
Our problem is now how to select the model that reproduces the data better. We focus our selection problem on the ability of the models to reproduce the price-change process at different time scales. The selection problem does not involve the spread process, s (t). In this case, we study a sample of N = 348, 253 price-change observations from the MSFT (Microsoft) stock.
We study this selection problem by means of the concepts developed in Section 2.1. First, we compute the Jensen–Shannon distance between two realizations of the real process. To this end, we divide the sample into two non-overlapping samples, each of length N/2, and we compute the two frequency vectors, and , for each value of m. We then compute the Jensen–Shannon distance, . It is clear that this is only one of the possible values of the random variable, JS, and we expect that it will be affected by some kind of fluctuations. Then, we generate Nr = 25 synthetic samples of length N/2 of processes corresponding to our three models. In this way, we compute Nr different frequencies that allow us to compute the sample averages:
Our analysis has been performed by using the Jensen–Shannon distance. However, other distances between probability distributions exist, such as the Kolmogorov–Smirnov distance [14], the Euclidean distance and the Hellinger distance [41]. We have repeated the analysis with these distances, and we found that its ability to select between competing models is smaller than that of Jensen–Shannon distance. In particular, Kolmogorov–Smirnov distance is able to discriminate models only until the scale m ≈ 100, which means that for this measure of discrepancy after m = 100, the models reproduce the sample distribution in the same way. In our framework, the distance with major discriminant power should be able to discriminate models for high values of the aggregation scale, m. The Hellinger and Euclidean distances, instead, have a discriminant power that is similar to that of Jensen–Shannon distance.
4. Conclusions
One important issue for the study of price dynamics is the selection and validation of a statistical model against the empirical data. Usually, financial time-series models that work well at a fixed time scale do not work comparably well at different time scales. The Jensen–Shannon distance analysis that we have performed enables us to perform an accurate test of goodness of our statistical models and to select among a pool of competing models. We have performed the same model selection procedure with different statistical distances. We find that their power to discriminate between different competing models is not larger than that of Jensen–Shannon distance. Moreover for the Jensen–Shannon distance, we have a good control of the finite sample properties.
Our analysis demonstrates that, for large tick assets, the coupling between mid-price dynamics and spread dynamics is important to account for the mid-price dynamics from the time scale of a single transaction to the time scale of one trading day.
We believe that the described method, based on the Jensen–Shannon distance, could be used also in contexts different from the financial one investigated in this work. This method could be useful each time we want to perform a multiscale test for a model against the empirical data samples.
Acknowledgments
The authors acknowledge partial support by the grant, SNS11LILLB “Price formation, agents heterogeneity, and market efficiency”.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bouchaud, J.-P.; Potters, M. Theory of Financial Risks: From Statistical Physics to Risk Management; Cambridge University Press: New York, NY, USA, 2003. [Google Scholar]
- Cont, R. Empirical properties of asset returns: Stylized facts and statistical issues. Quantit. Financ 2001, 1, 223–236. [Google Scholar]
- Gopikrishnan, P.; Plerou, V.; Amaral, L.A.N.; Meyer, M.; Stanley, H.E. Scaling of the distribution of fluctuations of financial market indices. Phys. Rev. E 1999, 60, 5305–5316. [Google Scholar]
- Mandelbrot, B.B. Fractals and Scaling in Finance; Springer: New York, NY, USA, 1997. [Google Scholar]
- Cont, R.; Tankov, P. Financial Modelling with Jump Processes; Chapman & Hall/CRC Press: Boca-Raton, FL, USA, 2004. [Google Scholar]
- Bacry, E.; Delour, J.; Muzy, J.F. Modelling financial time series using multifractal random walks. Physica A 2001, 299, 84–92. [Google Scholar]
- Ding, Z.; Granger, W.J.; Engle, R.F. A long memory property of stock market returns and a new model. J. Empir. Financ 1995, 1, 83–93. [Google Scholar]
- Micciche, S.; Bonanno, G.; Lillo, F.; Mantegna, R.N. Volatility in financial markets: Stochastic models and empirical results. Physica A 2002, 314, 756–761. [Google Scholar]
- Endres, D.M.; Schindelin, J.E. A new metric for probability distributions. IEEE Trans. Inform. Theor 2003, 49, 1858–1860. [Google Scholar]
- Connor, R.; Cardillo, F.A.; Moss, R.; Rabitti, F. Evaluation of Jensen–Shannon Distance over Sparse Data. In Similarity Search and Applications; Brisaboa, N., Ed.; Springer-Verlag Berlin: Heidelberg, Germany, 2013; pp. 163–168. [Google Scholar]
- Lin, J. Divergence measures based on the shannon entropy. IEEE Trans. Inform. Theor 1991, 37, 145–151. [Google Scholar]
- Robert, C.Y.; Rosenbaum, M. A new approach for the dynamics of ultra-high-frequency data: The model with uncertainty zones. J. Financ. Econometr 2011, 9, 344–366. [Google Scholar]
- Garèche, A.; Disdier, G.; Kockelkoren, J.; Bouchaud, J.P. Fokker-planck description for the queue dynamics of large tick stocks. Quantit. Financ 2012, 12, 1395–1419. [Google Scholar]
- Conover, W.J. A. Kolmogorov goodness-of-fit test for discontinuous distributions. J. Am. Stat. Assoc 1972, 67, 591–596. [Google Scholar]
- Curato, G.; Lillo, F. Modeling the coupled return-spread high frequency dynamics of large tick assets. 2013. arXiv:1310.4539. [Google Scholar]
- Basseville, M. Divergence measures for statistical data processing—An annotated bibliography. Signal Process 2013, 93, 621–633. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Smith, A.; Naik, P.A.; Tsai, C. Markov-switching model selection using Kullback-Leibler divergence. J. Econometr 2006, 134, 553–577. [Google Scholar]
- De Domenico, M.; Insolia, A. Entropic approach to multiscale clustering analysis. Entropy 2012, 14, 865–879. [Google Scholar]
- Contreras-Reyes, J.E; Arellano-Valle, R.B. Kullback-Leibler Divergence measure for multivariate skew-normal distributions. Entropy 2012, 14, 1606–1626. [Google Scholar]
- Tumminello, M.; Lillo, F.; Mantegna, R.N. Kullback-Leibler distance as a measure of the information filtered from multivariate data. Phys. Rev. E 2007, 76, 031123:1–031123:12. [Google Scholar]
- Quiroga, R.Q.; Arnhold, J; Lehnertz, K.; Grassberger, P. Kulback-Leibler and renormalized entropies: Applications to electroencephalograms of epilepsy patients. Phys. Rev. E 2000, 62, 8380–8386. [Google Scholar]
- Roldán, É.; Parrondo, J.M.R. Entropy production and Kullback-Leibler divergence between stationary trajectories of discrete systems. Phys. Rev. E 2012, 85, 031129:1–031129:12. [Google Scholar]
- Kullback, S. Information Theory and Statistics; Dover Publications: New York, NY, USA, 1968. [Google Scholar]
- Crooks, G.E.; Sivak, D.A. Measures of trajectory ensemble disparity in nonequilibrium statistical dynamics. J. Stat. Mech 2011, P06003. [Google Scholar]
- Majtey, A.P.; Lamberti, P.W.; Prato, D.P. Jensen–Shannon divergence as a measure of distinguishability between mixed quantum states. Phys. Rev. A 2005, 72, 052310:1–052310:6. [Google Scholar]
- Crooks, G.E. Measuring thermodynamic length. Phys. Rev. Lett 2007, 99, 100602:1–100602:4. [Google Scholar]
- Carpi, L.C.; Rosso, O.A.; Saco, P.M.; Ravetti, M.C. Analyzing complex networks evolution trough information theory quantifiers. Phys. Let. A 2011, 375, 801–804. [Google Scholar]
- Chekmarev, S.F. Information entropy as a measure of nonexponentiality of waiting-time distributions. Phys. Rev. E 2008, 78, 066113:1–066113:7. [Google Scholar]
- Felizzi, F.; Comoglio, F. Network-of-queues approach to B-cell-receptor affinity discrimination. Phys. Rev. E 2012, 85, 061926:1–061926:18. [Google Scholar]
- Hosoya, A.; Buchert, T.; Morita, M. Information entropy in cosmology. Phys. Rev. Lett 2004, 92, 141302:1–141302:4. [Google Scholar]
- Basharin, G.P. On a statistical estimate for the entropy of a sequence of independent random variables. Theor. Prob. Appl 1959, 4, 333–338. [Google Scholar]
- Herzel, H.; Schmitt, A.O.; Ebeling, W. Finite sample effects in sequence analysis. Chaos Soliton. Fract 1994, 4, 97–113. [Google Scholar]
- Schürmann, T.; Grassberger, P. Entropy estimation of symbol sequences. Chaos 1996, 6. [Google Scholar]
- Roulston, M.S. Estimating the errors on measured entropy and mutual information. Physica D 1999, 125, 285–294. [Google Scholar]
- Grassberger, P. Finite sample corrections to entropy and dimension estimates. Phys. Lett. A 1988, 128, 369–373. [Google Scholar]
- Grosse, I.; Bernaola-Galván, P.; Carpena, P.; Román-Roldán, R.; Oliver, J.; Stanley, H.E. Analysis of symbolic sequences using the Jensen–Shannon divergence. Phys. Rev. E 2002, 65, 041905:1–041905:16. [Google Scholar]
- Johnson, N.L.; Kemp, W.A.; Kotz, S. Univariate Discrete Distributions, 3nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Plerou, V.; Gopikrishnan, P.; Stanley, H.E. Quantifying fluctuations in market liquidity: Analysis of the bid-ask spread. Phys. Rev. E 2005, 71, 046131:1–046131:8. [Google Scholar]
- Ponzi, A.; Lillo, F.; Mantegna, R.N. Market reaction to a bid-ask spread change: A power-law relaxation dynamics. Phys. Rev. E 2009, 80, 016112:1–016112:12. [Google Scholar]
- Guha, S.; McGregor, A.; Venkatasubramanian, S. Streaming and sublinear approximation of entropy and information distances. 2005. arXiv:cs/0508122.. [Google Scholar]

© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Curato, G.; Lillo, F. Multiscale Model Selection for High-Frequency Financial Data of a Large Tick Stock by Means of the Jensen–Shannon Metric. Entropy 2014, 16, 567-581. https://doi.org/10.3390/e16010567
Curato G, Lillo F. Multiscale Model Selection for High-Frequency Financial Data of a Large Tick Stock by Means of the Jensen–Shannon Metric. Entropy. 2014; 16(1):567-581. https://doi.org/10.3390/e16010567
Chicago/Turabian StyleCurato, Gianbiagio, and Fabrizio Lillo. 2014. "Multiscale Model Selection for High-Frequency Financial Data of a Large Tick Stock by Means of the Jensen–Shannon Metric" Entropy 16, no. 1: 567-581. https://doi.org/10.3390/e16010567
APA StyleCurato, G., & Lillo, F. (2014). Multiscale Model Selection for High-Frequency Financial Data of a Large Tick Stock by Means of the Jensen–Shannon Metric. Entropy, 16(1), 567-581. https://doi.org/10.3390/e16010567




