Multiple Solutions of Nonlinear Boundary Value Problems of Fractional Order: A New Analytic Iterative Technique
Abstract
: The purpose of this paper is to present a new kind of analytical method, the so-called residual power series, to predict and represent the multiplicity of solutions to nonlinear boundary value problems of fractional order. The present method is capable of calculating all branches of solutions simultaneously, even if these multiple solutions are very close and thus rather difficult to distinguish even by numerical techniques. To verify the computational efficiency of the designed proposed technique, two nonlinear models are performed, one of them arises in mixed convection flows and the other one arises in heat transfer, which both admits multiple solutions. Graphical results and tabulate data are presented and discussed quantitatively to illustrate the multiple solutions. The results reveal that the method is very effective, straightforward, and powerful for formulating these multiple solutions.1. Introduction
Multiple or dual solutions of nonlinear boundary value problems (BVPs) of fractional order are an interesting subject in the area of mathematics, physics, and engineering. In fact, it is more consequential not to lose any solution of nonlinear BVPs of fractional order due to their wide application in scientific and engineering research. Based on this important fact, the present paper is going to present an analytical method, the so-called residual power series (RPS), that enables us to predict the multiplicity of solutions which nonlinear BVP of fractional order admits and furthermore to calculate the multiple solutions analytically at the same time.
BVPs of fractional order have received considerable attention in the recent years due to their wide applications in the areas of physics and engineering. Many important phenomena in electromagnetics, acoustics, viscoelasticity, electrochemistry, and material science are well described by fractional BVP [1–4]. It is well known that the fractional order differential and integral operators are non-local operators. This is main reason why differential operators of fractional order provide an excellent instrument for description of memory and hereditary properties of various physical and engineering processes. For example, half-order derivatives and integrals proved to be more useful for the formulation of certain electrochemical problems than the classical models [5–9]. Indeed, for example, applying fractional calculus theory to entropy theory has become a significant part and a hotspot research domain [10–19], since the fractional entropy could be used in the formulation of algorithms for image segmentation where traditional Shannon entropy has presented limitations [13] and in the analysis of anomalous diffusion processes and fractional diffusion equations [14–19].
In general, most BVPs of fractional order do not have exact solutions. Particularly, there is no known method for solving these types of equations in closed form solution. As a result, numerical and analytical techniques have been used to study such problems. The reader is referred to [20–27] in order to know more details about the fractional BVPs, including their history and kinds, their existence and uniqueness of solution, their applications and methods of solutions, etc.
Series expansions are a very important aid in numerical calculations, especially for quick estimates made in hand calculations, for example, in evaluating functions, integrals, or derivatives. Solutions to differential equations can often be expressed in terms of series expansions. Since, the advent of computers, it has, however, become more common to treat differential equations directly, using different approximation method instead of series expansions, but in connection with the development of automatic methods for formula manipulation, one can anticipate renewed interest in series methods. These methods have some advantages, especially in multidimensional and multiple solutions for BVPs of fractional order.
The RPS method was developed by the first author [28] as an efficient method for determining values of coefficients of the power series solution for first and the second-order fuzzy differential equations. It has been successfully applied in the numerical solution of the generalized Lane-Emden equation, which is a highly nonlinear singular differential equation [29] and in the numerical solution of higher-order regular differential equations [30]. The RPS method is an effective and easy to construct power series solution for strongly linear and nonlinear equations without linearization, perturbation, or discretization [28–30]. Different from the classical power series method, the RPS method does not need to compare the coefficients of the corresponding terms and a recursion relation is not required. This method computes the coefficients of the power series by a chain of equations of one or more variables. In fact, the RPS method is an alternative procedure for obtaining analytic solutions for BVPs of fractional order that admits multiple solutions. By using the residual error concept, we get a series solution, in practice a truncated series solution. Moreover, the multiple solutions and all their fractional derivatives are applicable for each arbitrary point in the given interval. On the other aspect as well, the RPS method does not require any conversion while switching from the low-order to the higher-order; as a result the method can be applied directly to a given problem by choosing an appropriate initial guess approximation.
In the present paper, the RPS method will investigate how to construct new algorithms for predicting and finding multiple solutions for those nonlinear BVPs of fractional order that admit multiple solutions. Furthermore, we will adapt a new generalization of Taylor’s series formula that involves Caputo fractional derivatives in order to apply the RPS method.
The results dealing with multiple solutions of BVPs of fractional order are relatively scarce. Recently, many authors have discussed the multiple solutions to some problems using some of the well-known methods. However, the reader is referred to [31–35] in order to know more details about these methods, including their types and history, their motivation for use, their characteristics, and their applications. On the other hand, the numerical solvability of other version of differential equations and other related equations can be found in [36–43] and references therein.
The outline of the paper is as follows: in the next section, we utilize some necessary definitions and results from fractional calculus theory. In Section 3, the general form of generalized Taylor’s formula is mentioned and proved. In Section 4, basic idea of the RPS method is presented in order to construct and predict multiple solutions for BVPs of fractional order. In Section 5, two nonlinear models are performed in order to illustrate the capability and simplicity of proposed method. Finally, conclusions are presented in Section 6.
2. Review of Fractional Calculus Theory
In this section, we present some necessary definitions and essentials results from fractional calculus theory. There are various definitions of fractional integration and differentiation, such as Grunwald-Letnikov’s definition and Riemann-Liouville’s definition [5,6,8]. The Riemann-Liouville derivative has certain disadvantages when trying to model real-world phenomena with fractional differential equations (FDEs). Therefore, we shall introduce a modified fractional differential operator proposed by Caputo in his work on the theory of viscoelasticity [4]. Throughout this paper, ℕ the set of integer numbers, ℝ the set of real numbers, and Γ is the Gamma function.
Definition 2.1: A real function f(x), x > 0 is said to be in the space Cμ, μ ∈ ℝ if there exists a real number p > μ such that f(x) = xp f1(x), where f1(x) ∈ C[0, ∞), and it is said to be in the space if f(n) (x) ∈ Cμ, n ∈ ℕ.
Definition 2.2: The Riemann-Liouville fractional integral operator of order α ≥ 0 of f ∈ Cμ, μ ≥ −1 is defined as:
Definition 2.3: The Caputo fractional derivative of order α > 0 of , n ∈ ℕ is defined as:
On the one hand, for some certain properties of the operator , it is obvious that when γ > −1, x > s ≥ 0, and C ∈ ℝ, we have and . On the other hand, properties of the operator can be summarized shortly in the form of the following: for f ∈ Cμ, μ ≥ −1, α, β ≥ 0, C ∈ ℝ, and γ ≥ −1, we have , , and .
Theorem 2.1: If n − 1 < α ≤ n, , n ∈ ℕ, and μ ≥ −1, then and , where x > s ≥ 0.
3. General form of Generalized Taylor’s Formula
In this section, we will introduce general form of generalized Taylor’s formula that contains the Caputo definition for fractional derivatives. In fact, we need this generalization in the application of the RPS method in order to predict and find the multiplicity of solutions.
We will begin with the following definition which is needed throughout this work, especially, in the two succeeding sections. After that, we present a new and a fundamental theorem called general form of generalized Taylor’s formula, which can formulate any function with certain properties in term of its fractional power series (FPS) representation.
Definition 3.1: A power series of the form
As a special case, when t0 = 0, the expansion is called a fractional Maclaurin series. Notice that in writing out the term corresponding to n = 0 and k = 0 in Equation (3) we have adopted the convention that (t − t0)0 = 1 even when t = t0. Also, when t = t0 each of terms of Equation (3) are vanished for n ≠ 0 ∧ k ≠ 0 and so. On the other hand, the FPS representation of Equation (3) always converges when t = t0. In the next lemma by we mean that (n times).
Lemma 3.1: Suppose that f(t) ∈ C[t0, t0 + R) and for j = 0, 1, 2, …, n + 1 where 0 ≤ m − 1 < α ≤ m. Then we have:
Proof: From the definition of the operator and by using the second mean value theorem for fractional integrals, one can find:
Theorem 3.1: Suppose that f(t) ∈ C[t0, t0 + R), , and can be differentiated (m − 1)-times on (t0, t0 + R) for j = 0,1,2, …, n +1, where 0 ≤ m − 1 < α ≤ m. Then:
Proof: From the certain properties of the operator , we have:
On the other direction, if we keep the repeating of this process, then after n-times of computations, we will obtain:
Thus, by using Lemma 3.1, the proof of the theorem will be complete.
Remark 3.1: We mention here that, if we fixed m = 1, then the series representation of f in Theorem 3.1 will leads to the following expansion of f about t0:
As with any convergent series, this means that f(t) is the limit of the sequence of partial sums. In the case of general form of generalized Taylor’s series, the partial sums are given as . In general, f(t) is the sum of its general form of generalized Taylor’s series if f(t) = limn→∞Tn(t). But on the other aspect as well, if we set Rn(t) = f(t) − Tn(t) then Rn(t) is the remainder of general form of generalized Taylor’s series. That is, , t0 ≤ ζ ≤ t < t0 + R.
Corollary 3.1: If on t0 ≤ t ≤ d, where m < α ≤ m − 1, then the reminder Rn(t) of general form of generalized Taylor’s series satisfies the inequality:
4. RPS Method for BVPs of Fractional Order
In this section, we predict and find multiple solutions for BVPs of fractional order that admit multiple solutions by substituting a FPS expansion with undetermined coefficients through the given equation. From the FDE a recursion formula for the computation of the coefficients was derived. On the other hand, the coefficients in the FPS expansion can be computed recursively by differentiating the FDEs.
For convenience, the reader is referred to [28–30] in order to know more details about the classical RPS methods, including their construction, their motivation for use, their characteristics compared to the conventional method, and their applications for solving different categories of linear and nonlinear differential equations of different types and orders.
In fact, the main goal of our work is to predict and find out multiple series solutions for nonlinear BVPs of fractional order. To illustrate the basic idea of the RPS method for solving fractional BVPs analytically, we first consider the following nonlinear fractional functional equation:
The crucial step of the RPS method for solving Equations (11) and (12) analytically is based on the fact that the boundary conditions of Equation (12) should be transcribed into equivalent form, so that, the new version conditions involves an unknown parameter so-called prescribed parameter δ and are split to:
In order to apply the RPS method in the fractional sense, we assume firstly that we can apply the operator , j = 0,1,…, m − 1, i = 0,1,… on the term of [u(r)] in Equation (14) and also we suppose that all solutions u(r) that satisfy Equations (14) and (15) can be expanded by FPS representation as follows:
Assume that Equation (14) satisfies the initial conditions u(i) (r0) = δi, i = 0, 1, 2, ..., m − 1, with δi as a prescribed parameters, where the unknown parameters δi can be determined later by substituting u(α) = β and/or any other constraint conditions into the obtained solution form. It is worth noting that some of δi may be known from the given initial conditions in Equation (15). As the first step in the prediction of multiple solutions, we set u0,0 be as an initial guess approximation of exact function solution u(r) of Equation (14). On the other hand, u0,0 will be of the form u0,0 = u0,0(r; δ0, δ1,…,δm−1) which satisfies the known initial conditions in Equation (15) automatically. It was proved in [28–30] that the coefficients c0j in Equation (16) will take the form , j = 0,1,2,…,m − 1. Therefore, we can consider the expansion formula:
Again, as the second step in the prediction of multiple solutions, we will let the double (k,l) to denote the (k,l)-truncated series approximation of u(r). That is:
Prior to applying the RPS technique for finding the values of coefficients cij in the series expansion of Equation (19), we must define the residual function concept for the main nonlinear fractional functional Equation (14) as , r ≥ r0 and the following truncated (k,l)-resudial function:
As in [28–30], it is clear that Res(r) = 0 for each r ∈ [r0,r0 + R), where R is the radius of convergence of Equation (18). In fact, this shows that for each i = 1, 2, 3, …,k and j = 0, 1, 2, …,l, since the fractional derivative of a constant function in the Caputo sense is zero. In the mean time, the fractional derivatives for each i = 1, 2, 3, …,k and j = 0, 1, 2, …,l of Res(r) and Res(i,j)(r) are matching at r = r0; it is obvious that:
To obtain the value of coefficients cvw in Equation (19) for v = 1, 2, 3, …, k and w = 0, 1, 2, …, l, we apply the following subroutine: substitute (v, w)-truncated series approximation of u(r) into Equation (20), find the fractional derivative formula of Res(v,w) (r) at r = r0, and then finally solve the obtained algebraic equation to get the required coefficients.
To summarize the computation process of RPS method in numerical values, we apply the following: fixed i = 1 and run the counter j = 0, 1, 2, …, l to find (1,j)-truncated series expansion of suggested solution, next fixed i = 2 and run the counter j = 0, 1, 2, …, l to obtain the (2,j)-truncated series, and so on. In fact, to get (1,0)-truncated series expansion for Equations (14) and (15), we use Equation (19) and write:
On the other hand, to determine the value of first unknown coefficient, c1,0, in Equation (22), we should substitute Equation (22) into both sides of the (1,0)-residual function that obtained from Equation (20), to get the following result:
Now, depending on the result of Equation (21) for (i,j) = (1,0), Equation (23) gives . Hence, using the (1,0)-truncated series expansion of Equation (22), the (1,0)-RPS approximation for Equations (14) and (15) can be expressed as:
Similarly, to find (1,1)-truncated series expansion for Equations (14) and (15), we use Equation (19) and write:
Again, to find out the value of second unknown coefficient, c11 in Equation (25), we must find and formulate (1,1)-residual function based on Equation (20) and then substitute the form of u1,1(r) in Equation (25) to find new discretized form of this residual function as follows:
Now, using the fact that Dr0 Res(1,1)(r0) = 0, we can easily obtain:
Hence, using the (1,1)-truncated series expansion of Equation (25), the (1,1)-RPS approximation for Equations (14) and (15) can be expressed as:
This procedure can be repeated till the arbitrary order coefficients of FPS solution for Equations (14) and (15) are obtained. Moreover, higher accuracy can be achieved by evaluating more components.
Remark 4.1: It is worth indicating that there are still unknown prescribed parameters δi in the series expansion of Equation (19) (and simply in Equation (29)) that should be determined. It is essential that the existence of a unique or multiple solutions in terms of Equation (19) (and simply in Equation (29)) for the original BVP which is covered by Equations (11) and (12) depends on the fact that whether the forcing condition u(α) = β and/or any other constraint condition in Equation (13) admits a unique or multiple values for the formally introduced prescribed parameters δi. This stage is called rule of multiplicity of solutions that is a criterion in order to know how many solutions the BVP in Equations (11) and (12) admits.
Anyhow, as the final step in the construction, if we substitute u(α) = β and/or any other constraint conditions into the obtained solution form of Equation (19) (and simply in Equation (29)), then we obtain a system of nonlinear algebraic equations in the prescribed variables δ0, δ1, δ2, …, δm−1(here, we must recall that some of δi, i = 0,1,…, m −1 may be known from Equation (15)) which can be easy solved using symbolic computation software such as MAPLE 13 or MATHEMATICA 7.0. In fact, if we substitute these values of prescribed parameters in the obtained solution form of Equation (19) (and simply in Equation (29)), then discretized form of the (k, l)-truncated series approximation of u(r) of Equations (11) and (12) (and simply (1,1)-truncated series approximation of u(r) as given by Equation (26)) will be obtained.
5. Applications and Numerical Discussions
The application problems are carried out using the proposed RPS method, which is one of the modern analytical techniques because of its iterative nature; it can handle any kind of boundary conditions and other constraints. The RPS method doesn’t have mathematical requirements about the multiple solutions of fractional BVPs to be solved; the RPS method is also very effective in identifying global predicted solutions, and provides a great flexibility in choosing the initial guess approximations. However, in order to verify the computational efficiency of the designed RPS method, two nonlinear models are performed, one of them arises in mixed convection flows and the other one arises in heat transfer, which both admit multiple solutions. In the process of computation, all the symbolic and numerical computations were performed by using the MATHEMATICA 7.0 software package.
Throughout this section, we will try to give the results of the two applications; however, in some cases we will switch between the results obtained for the applications in order not to increase the length of the paper without the loss of generality for the remaining application and results. However, by easy calculations we can collect further results and discussion for the desire application.
Application 5.1: The aim of this application is to apply the RPS method to analyze a kind of model in mixed convection flows namely, combined forced and free flow in the fully developed region of a vertical channel with isothermal walls kept at the same temperature. In this model, the fluid properties are assumed to be constant and the viscous dissipation effect is taken into account. The set of governing balance equations for the velocity field is reduced to the following [45,46]:
Next, we will show how one can find out the existence of multiple solutions for Equations (30) and (31) in aforesaid range for 0 ≤ y ≤ 1. To do so, we consider firstly Equations (30) and (31) and suppose that u(0) = δ0 and u″(0) = δ2. So, Equations (30) and (31) can be modified into the following form:
Now, we apply the RPS method on Equations (32) and (33), where prescribed parameters δ0 and δ2 which are played an important and fundamental role to realize about multiplicity of solutions, will be obtained later by substituting the additional forcing condition and the additional constraint condition in resulting expansion formula that approximate Equations (32) and (33).
According to Equation (18), we assume that the series solution of Equations (32) and (33) can be written as:
However, to determine the value of coefficient c10, we find out (1,0)-truncated series approximation of u(y) as and (1,0)-residual function as . On the other aspect as well, by using Equation (21) for (i, j) = (1,0) and substituting y= 0, we obtain c10 = 0.
Similarly, to find the value of coefficient c11, we evaluate (1,1)-truncated series approximation of u(y) as and (1,1)-residual function as . Thus, for (i, j) = (1,1), we conclude that , while the substitution of y = 0 leads to c11 = 0.
To evaluate the value of coefficient c12, we need to write and . However, by considering the fact that , we can easily find . Similarly, the continuation in the same manner will leads also to c13 = 0. According to the initial guess approximation and the form of terms in Equation (32) taking into account the form of Equations (35) and (36), we can conclude that cij = 0 for j = 0,1,3. Therefore, according to Equation (34) the FPS solution of Equations (32) and (33) can be written in the form of the following expansion:
Again, to determine the value of coefficient c22, we need solve the equation which gives . Similarly, we have , and so on. Consequently, based on the structure of Equation (38) the (3,2)-truncated series approximation of u(y) generated from the RPS method can be written as:
It is clear that, Equation (39) contain two unknown certain parameters which are δ0 and δ2. To determine their introductory values substituting the forcing condition u(1) = 0 and the constraint condition , and finally selecting some numerical values of Ψ.
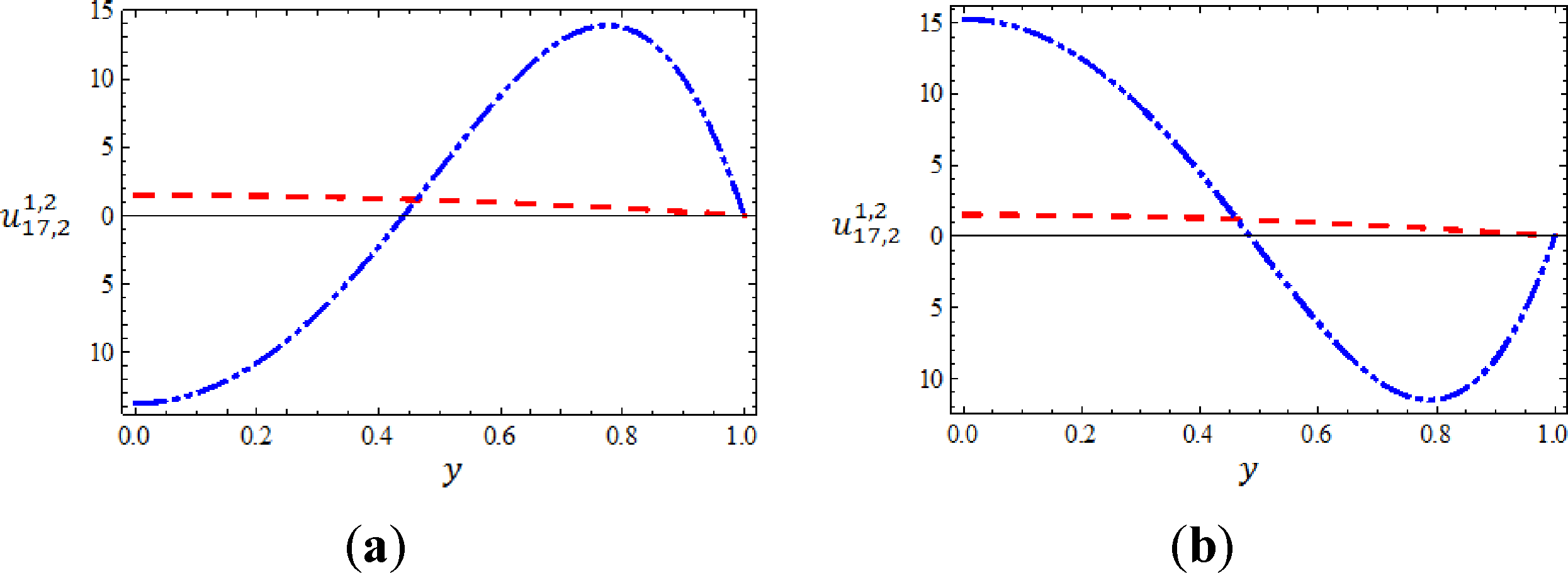
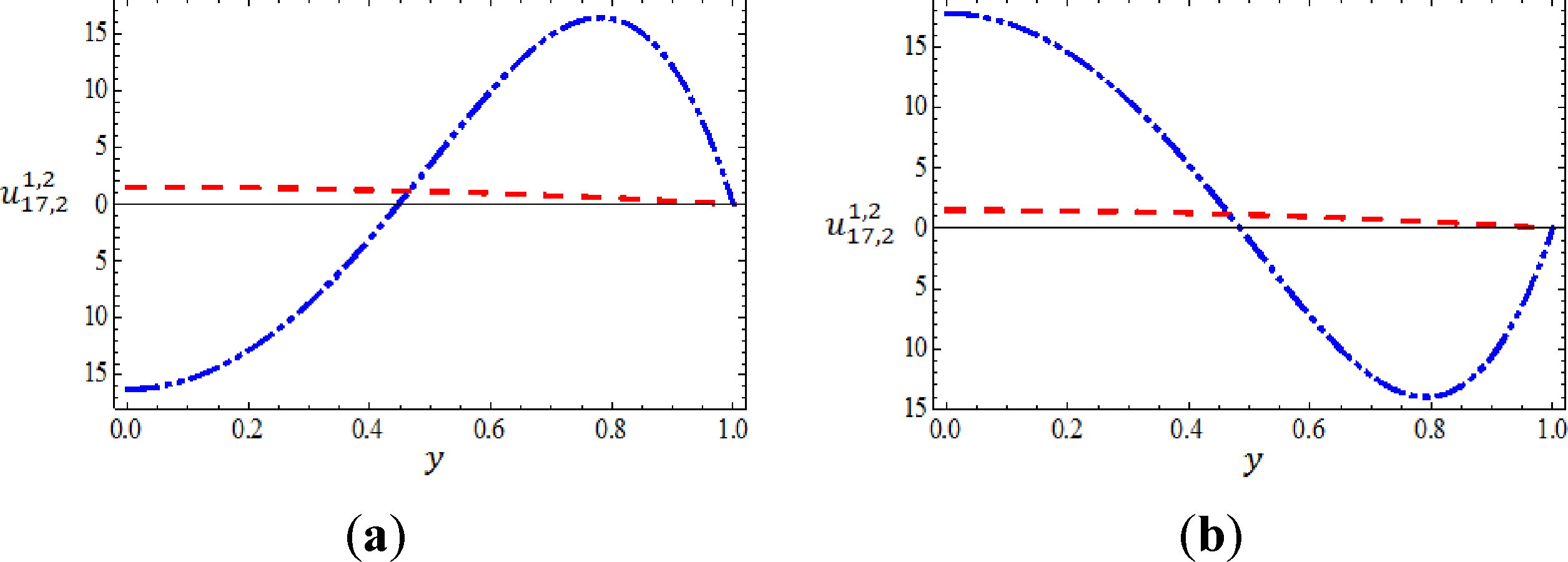
Now, to be specific, we consider two cases according to Equation (39) which consist of Ψ = −20 and Ψ = 20. On the other hand, we generate and obtain the (17,2)-truncated series approximation of u(y) using the same procedure. However, various values of δ0 and δ2 have been calculated and listed in Tables 1 and 2 when α = 3.9 and when α = 4, respectively. For simplicity and not to conflict, we will let to denote the first approximate solution of u(y) and to denote the second approximate solution of u(y).
Consequently, we conclude that the RPS method furnishes multiple solutions for Equations (30) and (31). It is worth mentioning here that when α= 3.9, Table 1 indicates the existence of two solutions at Ψ = −20, so that, u(0) = 1.489853467004, u″(0) = −2.908126478404 for the first branch solution and u(0) = −13.71508112423, u″(0) = 148.3654474295 for the second branch solution. In fact, these results answer the question how many solutions the nonlinear BVP in Equations (30) and (31) admits? The same procedure has been done at the case Ψ = 20. As we see from Table 1, there exist multiple solutions namely u(0) = 1.511205551820, u″(0) = −3.101976104073 for the first branch solution and u(0) = 15.29266790865, u″(0) = −139.7646425135 for the second branch solution. Similar conclusion can be achieved when α= 4 as shown in Table 2.
The RPS technique has an advantage that it is possible to pick any point in the interval of integration and as well the approximate multiple solutions and all their fractional derivatives will be applicable. In other words, continuous approximate solutions can be obtained. Our next goal, is to show the mathematical behavior of the obtained multiple solutions geometrically. To do so, we plot the first and the second solutions obtained from the (17,2)-truncated series approximation of u(y) at Ψ = −20 and Ψ = 20 when α = 3.9 in Figure 1, while in Figure 2 we depict the first and the second approximate solutions at the same values when α= 4.
The effective calculations of the two approximate branches solutions for Equations (30) and (31) with respect to some certain specific values of Ψ on u(0) and u″(0) is explored next in which the obtained results are generated from the (17,2)-truncated series approximation of u(y). Table 3 gives the effect of the numeric value of Ψ when α= 3.9, while Table 4 gives the effect of the numeric value of Ψ when α= 4. The numeric value of Ψ lie within the range [−80,80] in step of 20. It is to be noted that, when the values of Ψ increasing gradually within mentioned range, the value of u″(0) decreasing as well as the value of u(0) increasing for both branch solutions and for both order of derivatives.
We mention here that, the case of Ψ = 0 correspond either to a very small viscous dissipation heating or to negligible buoyancy effects. However, Equations (30) and (31) are easily solved and admit the unique solution for both α= 3.9 and α = 4. On the other direction, from the last tables, it can be seen that our results of the RPS method agree best with method of [34] when α = 3.9 and method of [35] when α= 4.
To measure the accuracy and the efficiency of the proposed RPS method for predicting and finding the multiple solutions for Equations (30) and (31), we report the residual error function at Ψ = −20 and Ψ = 20 when α= 3.9 and when α= 4 in Tables 5 and 6, respectively, in which the obtained results are generated from the (17,2)-truncated series approximation of u(y). The residual error function is defined using Equation (35) in which the grid points are building as , i = 0, 1, 2, …, 10. For simplicity and not to conflict, we will let to denote the residual error function of the first approximate solution of u(y) and to denote the residual error function of the second approximate solution of u(y).
In fact, the residual errors measure the extent of agreement between the (17,2)th-order approximate RPS solutions and unknowns closed form solutions which are inapplicable in general for such nonlinear equations. However, from the tables, it can be seen that the RPS technique provides us with the accurate approximate solutions and explicates the rapid convergence in approximating the multiple solutions for Equations (30) and (31).
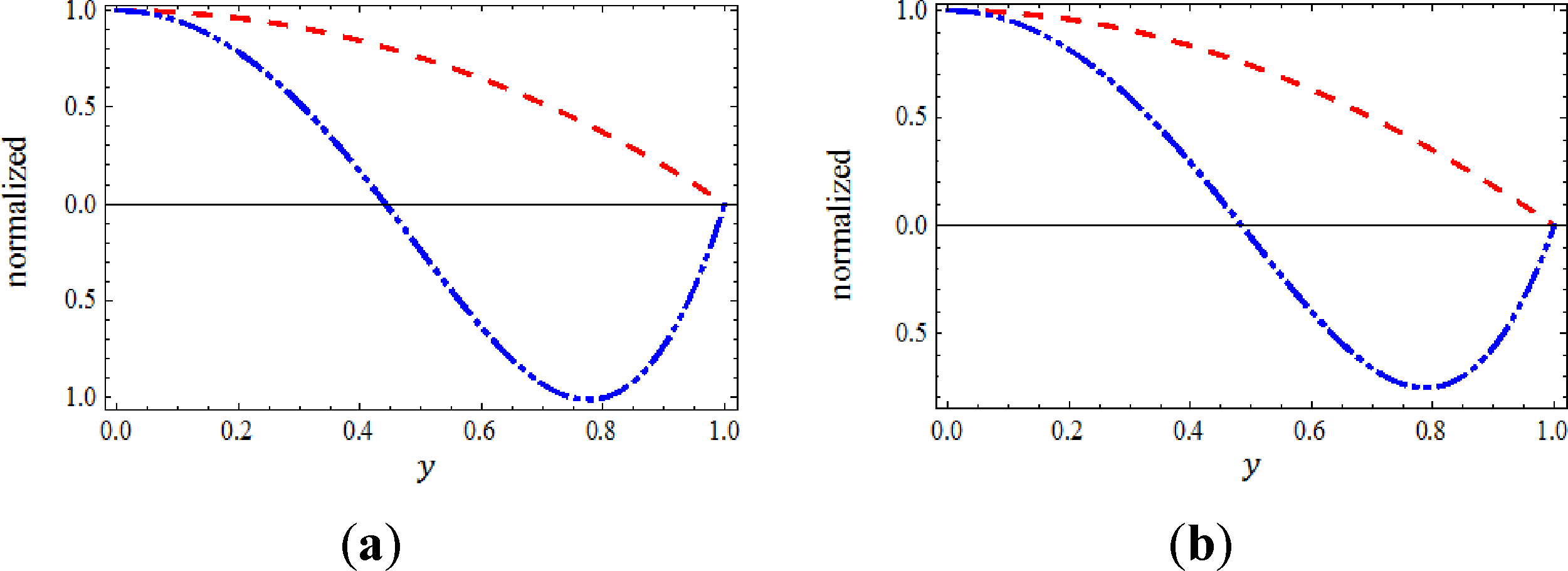
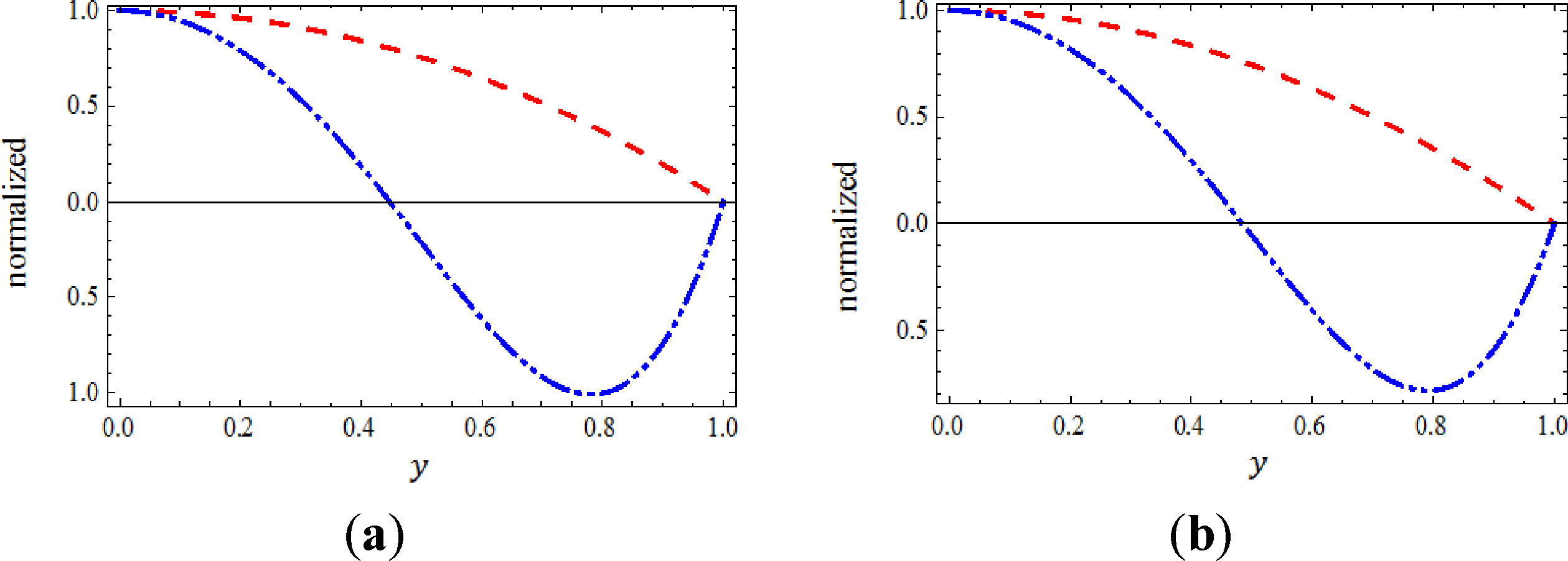
In Tables 7 and 8 we tabulate the values of the approximate multiple solutions at the final grid node y = 1 that generated from the (17,2)-truncated series approximation of u(y) at Ψ = 20 and Ψ = −20 when α = 3.9 and when α = 4. In fact, we do this to facilitate the calculations in order to show the validity and accuracy of the proposed RPS method in predicting and finding the multiple approximate solutions. In these tables, we can find that the values of , k = 1,2 agree nicely and completely the forcing condition u(1) = 0 and the constraint condition , k = 1,2.
In order to study the behavior of multiple approximate solutions in a better view, we plot the normalized of the two branch approximate solutions of Equations (30) and (31) with respect to , k = 1,2 at some specific values of Ψ and α in which the obtained results are generated from the (17,2)-truncated series approximation of u(y). However, Figure 3 shows the normalized function , k = 1,2 at Ψ = −20 and Ψ = 20 when α = 3.9, while Figure 4 shows the normalized function , k = 1,2 at Ψ = −20 and Ψ= 20 and when α = 4. In these figures, we can see the almost similarity in the behavior of the two branches approximate solutions at the two mentioned specific value of Ψ when α = 3.9 when α = 4.
Application 5.2: Fins are extensively used to enhance the heat transfer between a solid surface and its convective, radiative, or convective radiative surface. Finned surfaces are widely used, for instance, for cooling electric transformers, the cylinders of aircraft engines, and other heat transfer equipment. The temperature distribution of a straight rectangular fin with a power-law temperature dependent surface heat flux can be determined by the solutions of a one-dimensional steady state heat conduction equation which, in dimensionless form, is given as follows [47,48]:
The prediction and construction of multiple solutions for BVPs of fractional order is the fundamental target of this paper. Next, we will show in brief steps and calculations how we can predict and find out existence of multiple solutions for Equations (40) and (41). To do so, we consider firstly, Equations (40) and (41) and suppose that θ(0) = δ0. So, a new discretized form of Equations (40) and (41) can be obtained as follows:
Similar to the previous procedure and discussions that used in Application 5.1, the FPS solution and the residual function for Equations (42) and (43) will take, respectively, the following form:
It is to be noted that the (1,0)-truncated series solution of Equations (42) and (43) is θ10(x) = δ0 + c10xα and the (1,0)-residual function is . Thus, using Equation (21) for (i, j) = (1,0), we get . Similarly, the (1,1)-truncated series solution is and the (1,1)-residual function is:
More precisely, according to Equation (21) the solution of equation D0Res(1,1)(0) = 0 will gives c11 = 0. Thus, based on the initial guess approximation and the form of terms of Equation (42) taking into account the form of Equations (46) and (47), it easy to see that ci1 = 0, i = 1, 2, 3, …. Therefore, according to Equation (44) a new discretized form of FPS solution for Equations (42) and (43) can be obtained and expressed as:
In the shape of shapes by continuing in this procedure and using Equations (46) and (47) taking into account Equation (21), we can easily obtained that , , and so on. Consequently, based on Equation (50) the (3,0)-truncated series approximation of θ(x) generated from the RPS method can be written as:
It is clear that, all the terms in Equation (51) contain an unknown certain parameter δ0 and to determine its introductory values we must substitute the boundary condition θ(1) = 1 back into Equation (51) to obtain a nonlinear algebraic equation in one variable, which can be easy solved using symbolic computation software. But on the other aspect as well, if we generate and obtain (300,0)-truncated series approximation of θ(x) by using the same procedure discussed, then two various values of δ0 have been calculated and listed in Table 9 when α = 1.9 and when α = 2.
It is clear from the table that two δ-plateaus can be identified and consequently we conclude that the RPS method furnishes multiple solutions to Equations (40) and (41). It is worth mentioning here that Equation (46) (and simply Equation (51)) indicates existence of two solutions. On the other hand, the existence of a unique or multiple solutions in terms of Equation (46) (and simply Equation (51)) for the original BVP which is covered by Equations (40) and (41) depends on the fact that whether the forcing condition θ(1) = 1 admits a unique or multiple values for the formally introduced prescribed parameters δ0.
Finally, in Figure 5 we plot the first and the second approximate multiple solutions of Equations (40) and (41) that obtained from the (300,0)-truncated series approximation of θ(x) when α = 1.9 and when α= 2. In fact, we do this for the same reasons that mentioned in the Application 5.1, where the same conclusion can be obtained too. On the other direction, as in the previous application, we can see that the sketch of the two branches approximate RPS solutions that the problem admitted are agree best and nicely with method of [34] when α= 1.9 and method of [35] α= 2.
6. Conclusions
It is very important not to lose any solution of nonlinear FDEs with boundary conditions in engineering and physical sciences. In this regard, the present paper has introduced a new methodology namely the RPS method to prevent this, so that the presented method is not only able to predict the existence of multiple solutions, but also to calculate all branches of solutions effectively at the same time by using an appropriate initial guess approximation. We also noted that the RPS solutions were computed via a simple algorithm without any need for perturbation techniques, special transformations, or discretization. The validity of this method has been checked by two nonlinear models, one of them arises in mixed convection flows and the other one arises in heat transfer, which both admit multiple or dual solutions.
Acknowledgments
The authors would like to express their thanks to unknown referees for their careful reading and helpful comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Beyer, H.; Kempfle, S. Definition of physical consistent damping laws with fractional derivatives. Zeitschrift für Angewandte Mathematik und Mechanik 1995, 75, 623–635. [Google Scholar]
- He, J.H. Approximate analytic solution for seepage flow with fractional derivatives in porous media. Comput. Methods Appl. Mech. Eng 1998, 167, 57–68. [Google Scholar]
- He, J.H. Some applications of nonlinear fractional differential equations and their approximations. Bull. Sci. Technol 1999, 15, 86–90. [Google Scholar]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent: Part II. Geophys. J. Int 1967, 13, 529–539. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Mainardi, F. Fractional Calculus: Some Basic Problems in Continuum and Statistical Mechanics. In Fractals and Fractional Calculus in Continuum Mechanics; Carpinteri, A., Mainardi, F., Eds.; Springer: Wien, Austria, New York, NY, USA, 1997; pp. 291–348. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Oldham, K.B.; Spanier, J. The Fractional Calculus; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Luchko, Y.; Gorenflo, R. The Initial-Value Problem for Some Fractional Differential Equations with Caputo Derivative; Preprint Series A08–98; Fachbereich Mathematik und Informatic, Freie Universitat: Berlin, Germany, 1998. [Google Scholar]
- Ubriaco, M.R. Entropies based on fractional calculus. Phys. Lett. A 2009, 373, 2516–2519. [Google Scholar]
- Li, H.; Haldane, F.D.M. Entanglement spectrum as a generalization of entanglement entropy: Identification of topological order in non-abelian fractional quantum Hall effect states. Phys. Rev. Lett 2008, 101, 010504. [Google Scholar]
- Hoffmann, K.H.; Essex, C.; Schulzky, C. Fractional diffusion and entropy production. J. Non-Equilib. Thermodyn 1998, 23, 166–175. [Google Scholar]
- Machado, J.A.T. Entropy analysis of integer and fractional dynamical systems. Nonlinear Dyn 2010, 62, 371–378. [Google Scholar]
- Essex, C.; Schulzky, C.; Franz, A.; Hoffmann, K.H. Tsallis and Rényi entropies in fractional diffusion and entropy production. Physica A 2000, 284, 299–308. [Google Scholar]
- Cifani, S.; Jakobsen, E.R. Entropy solution theory for fractional degenerate convection-diffusion equations. Annales de l’Institut Henri Poincare (C) Non Linear Analysis 2011, 28, 413–441. [Google Scholar]
- Prehl, J.; Essex, C.; Hoffmann, K.H. Tsallis relative entropy and anomalous diffusion. Entropy 2012, 14, 701–706. [Google Scholar]
- Prehl, J.; Boldt, F.; Essex, C.; Hoffmann, K.H. Time evolution of relative entropies for anomalous diffusion. Entropy 2013, 15, 2989–3006. [Google Scholar]
- Prehl, J.; Essex, C.; Hoffmann, K.H. The superdiffusion entropy production paradox in the space-fractional case for extended entropies. Physica A 2010, 389, 215–224. [Google Scholar]
- Magin, R.L.; Ingo, C.; Colon-Perez, L.; Triplett, W.; Mareci, T.H. Characterization of anomalous diffusion in porous biological tissues using fractional order derivatives and entropy. Micropor. Mesopor. Mater 2013, 178, 39–43. [Google Scholar]
- Doha, E.H.; Bhrawy, A.H.; Ezz-Eldien, S.S. A Chebyshev spectral method based on operational matrix for initial and boundary value problems of fractional order. Comput. Math. Appl 2011, 62, 2364–2373. [Google Scholar]
- Al-Mdallal, Q.M.; Syam, M.I.; Anwar, M.N. A collocation-shooting method for solving fractional boundary value problems. Commun. Nonlinear Sci. Numer. Simul 2010, 15, 3814–3822. [Google Scholar]
- Al-Refai, M.; Hajji, M.A. Monotone iterative sequences for nonlinear boundary value problems of fractional order. Nonlinear Anal 2011, 74, 3531–3539. [Google Scholar]
- Pedas, A.; Tamme, E. Piecewise polynomial collocation for linear boundary value problems of fractional differential equations. J. Comput. Appl. Math 2012, 236, 3349–3359. [Google Scholar]
- Ahmad, B.; Nieto, J.J. Existence of solutions for nonlocal boundary value problems of higher-order nonlinear fractional differential equations. Abstr. Appl. Anal 2009, 2009, 494720. [Google Scholar]
- Shuqin, Z. Existence of solution for boundary value problem of fractional order. Acta Math. Sci 2006, 26B, 220–228. [Google Scholar]
- Bai, Z. On positive solutions of a nonlocal fractional boundary value problem. Nonlinear Anal. Theory Methods Appl 2010, 72, 916–924. [Google Scholar]
- El-Ajou, A.; Abu Arqub, O.; Momani, S. Solving fractional two-point boundary value problems using continuous analytic method. Ain Shams Eng. J 2013, 4, 539–547. [Google Scholar]
- Abu Arqub, O. Series solution of fuzzy differential equations under strongly generalized differentiability. J. Adv. Res. Appl. Math 2013, 5, 31–52. [Google Scholar]
- Abu Arqub, O.; El-Ajou, A.; Bataineh, A.; Hashim, I. A representation of the exact solution of generalized Lane-Emden equations using a new analytical method. Abstr. Appl. Anal 2013, 2013, 378593. [Google Scholar]
- Abu Arqub, O.; Abo-Hammour, Z.; Al-badarneh, R.; Momani, S. A reliable analytical method for solving higher-order initial value problems. Discret. Dyn. Nat. Soc 2013, 2013, 673829. [Google Scholar]
- Liao, S.J. An analytic approach to solve multiple solutions of a strongly nonlinear problem. Appl. Math. Comput 2005, 69, 854–865. [Google Scholar]
- Xu, H.; Liao, S.J. Dual solutions of boundary layer flow over an upstream moving plate. Commun. Nonlinear Sci. Numer. Simul 2008, 13, 350–358. [Google Scholar]
- Xu, H.; Lin, Z.L.; Liao, S.J.; Wu, J.Z.; Majdalani, J. Homotopy based solutions of the Navier-Stokes equations for a porous channel with orthogonally moving walls. Phys. Fluids 2010, 22. [Google Scholar] [CrossRef]
- Alomari, A.K.; Awawdeh, F.; Tahat, N.; Bani Ahmad, F.; Shatanawi, W. Multiple solutions for fractional differential equations: Analytic approach. Appl. Math. Comput 2013, 219, 8893–8903. [Google Scholar]
- Abbasbandy, S.; Shivanian, E. Predictor homotopy analysis method and its application to some nonlinear problems. Commun. Nonlinear Sci. Numer. Simul 2011, 16, 2456–2468. [Google Scholar]
- Abu Arqub, O.; Al-Smadi, M.; Momani, S. Application of reproducing kernel method for solving nonlinear Fredholm-Volterra integrodifferential equations. Abstr. Appl. Anal 2012, 2012, 839836. [Google Scholar]
- Abu Arqub, O.; Al-Smadi, M.; Shawagfeh, N. Solving Fredholm integro-differential equations using reproducing kernel Hilbert space method. Appl. Math. Comput 2013, 219, 8938–8948. [Google Scholar]
- Al-Smadi, M.; Abu Arqub, O.; Momani, S. A computational method for two-point boundary value problems of fourth-order mixed integrodifferential equations. Math. Probl. Eng 2013, 2013, 832074. [Google Scholar]
- Shawagfeh, N.; Abu Arqub, O.; Momani, S. Analytical solution of nonlinear second-order periodic boundary value problem using reproducing kernel method. J. Comput. Anal. Appl 2014, 16, 750–762. [Google Scholar]
- Abu Arqub, O.; El-Ajou, A.; Momani, S.; Shawagfeh, N. Analytical solutions of fuzzy initial value problems by HAM. Appl. Math. Inf. Sci 2013, 7, 1903–1919. [Google Scholar]
- El-Ajou, A.; Abu Arqub, O.; Momani, S. Homotopy analysis method for second-order boundary value problems of integrodifferential equations. Discret. Dyn. Nat. Soc 2012, 2012, 365792. [Google Scholar]
- Abu Arqub, O.; Abo-Hammour, Z.S.; Momani, S. Application of continuous genetic algorithm for nonlinear system of second-order boundary value problems. Appl. Math. Inf. Sci 2014, 8, 235–248. [Google Scholar]
- Abu Arqub, O.; Abo-Hammour, Z.S.; Momani, S.; Shawagfeh, N. Solving singular two-point boundary value problems using continuous genetic algorithm. Abstr. Appl. Anal 2012, 2012, 205391. [Google Scholar]
- Odibat, Z.; Shawagfeh, N. Generalized Taylor’s formula. Appl. Math. Comput 2007, 186, 286–293. [Google Scholar]
- Barletta, A. Laminar convection in a vertical channel with viscous dissipation and buoyancy effects. Int. J. Heat Mass Transf 1999, 26, 153–164. [Google Scholar]
- Barletta, A.; Magyari, E.; Keller, B. Dual mixed convection flows in a vertical channel. Int. J. Heat Mass Transf 2005, 48, 4835–4845. [Google Scholar]
- Kern, Q.D.; Kraus, D.A. Extended Surface Heat Transfer; McGraw-Hill: New York, NY, USA, 1972. [Google Scholar]
- Chang, M.H. A decomposition solution for fins with temperature dependent surface heat flux. Int. J. Heat Mass Transf 2005, 48, 1819–1824. [Google Scholar]

| Ψ | (0, Ψ) | (0, Ψ) | (0, Ψ) | (0, Ψ) |
|---|---|---|---|---|
| −20 | 1.489853467004 | −2.908126478404 | −13.71508112423 | 148.3654474295 |
| 20 | 1.511205551820 | −3.101976104073 | 15.29266790865 | −139.7646425135 |
| Ψ | (0, Ψ) | (0, Ψ) | (0, Ψ) | (0, Ψ) |
|---|---|---|---|---|
| −20 | 1.491429027619 | −2.923003985191 | −16.24366439412 | 170.0391846202 |
| 20 | 1.509327190185 | −3.084107676423 | 17.81653001586 | −161.7258228610 |
| Ψ | (0, Ψ) | (0, Ψ) | (0, Ψ) | (0, Ψ) |
|---|---|---|---|---|
| −80 | 1.464188372395 | −2.677900574103 | −2.804122381089 | 39.98989706426 |
| −60 | 1.472069208045 | −2.748246621431 | −4.021367259783 | 52.08059778256 |
| −40 | 1.480588602154 | −2.824645834495 | −6.448785247872 | 76.19140323508 |
| −20 | 1.489853467004 | −2.908126478404 | −13.71508112423 | 148.3654474295 |
| 0 | 1.5 | −3 | 1.5 | −3 |
| 20 | 1.511205551820 | −3.101976104073 | 15.29266790865 | −139.7646425135 |
| 40 | 1.523707257512 | −3.216343513749 | 5.590088525362 | −67.55959331340 |
| 60 | 1.537832713039 | −3.346267779136 | 8.023126702632 | −43.39506854926 |
| 80 | 1.554053587089 | −3.496312065964 | 4.364483870436 | −31.22440353861 |
| Ψ | (0, Ψ) | (0, Ψ) | (0, Ψ) | (0, Ψ) |
|---|---|---|---|---|
| −80 | 1.469261663095 | −2.725277968954 | −3.442692067043 | 45.35348443763 |
| −60 | 1.476139016516 | −2.786393212425 | −4.869349036038 | 59.24934656620 |
| −40 | 1.483504520962 | −2.852078148878 | −7.716406012298 | 86.98041469093 |
| −20 | 1.491429027619 | −2.923003985191 | −16.24366439412 | 170.0391846202 |
| 0 | 1.5 | −3 | 1.5 | −3 |
| 20 | 1.509327190185 | −3.084107676423 | 17.81653001586 | −161.7258228610 |
| 40 | 1.519550991842 | −3.176660397839 | 9.286966701002 | −78.64533628503 |
| 60 | 1.530855160142 | −3.279404862063 | 6.435961661508 | −50.87705915606 |
| 80 | 1.543486995118 | −3.394693823078 | 5.003537046217 | −36.92681430877 |
| yi | | (y, Ψ = −20)| | | (y, Ψ = 20)| | | (y, Ψ = −20)| | | (y, Ψ = 20)| |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0.1 | 1.94289029 × 10−16 | 1.94288750 × 10−16 | 3.97866979 × 10−13 | 3.69518622 × 10−13 |
| 0.2 | 6.66133776 × 10−16 | 6.66117073 × 10−16 | 1.36177362 × 10−12 | 1.25252855 × 10−12 |
| 0.3 | 1.22124324 × 10−15 | 1.33208244 × 10−15 | 2.23471544 × 10−12 | 2.28611754 × 10−12 |
| 0.4 | 2.22041113 × 10−15 | 1.99736092 × 10−15 | 4.17791163 × 10−12 | 3.58225102 × 10−12 |
| 0.5 | 2.66422469 × 10−15 | 2.66042643 × 10−15 | 8.58345468 × 10−12 | 6.93024293 × 10−12 |
| 0.6 | 3.99495362 × 10−15 | 3.53947330 × 10−15 | 5.43711567 × 10−10 | 3.45019238 × 10−10 |
| 0.7 | 4.43255151 × 10−15 | 3.51500060 × 10−15 | 1.66806846 × 10−7 | 4.67722166 × 10−8 |
| 0.8 | 6.18659833 × 10−15 | 5.22990386 × 10−15 | 1.60051841 × 10−3 | 5.20245588 × 10−4 |
| 0.9 | 5.23312894 × 10−15 | 5.08335790 × 10−15 | 4.48714378 | 1.46607132 |
| 1 | 6.84470511 × 10−15 | 6.53165847 × 10−15 | 5252.11818 | 1725.28045 |
| yi | | (y, Ψ = −20)| | | (y, Ψ = 20)| | | (y, Ψ = −20)| | | (y, Ψ = 20)| |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0.1 | 1.77635684 × 10−17 | 2.22041829 × 10−22 | 2.91038305 × 10−17 | 2.32842284 × 10−24 |
| 0.2 | 7.10542750 × 10−17 | 1.42080125 × 10−20 | 1.86264518 × 10−15 | 3.81774414 × 10−20 |
| 0.3 | 1.59872197 × 10−16 | 1.61706602 × 10−19 | 2.12167382 × 10−14 | 1.11809539 × 10−17 |
| 0.4 | 2.84218548 × 10−16 | 9.06583155 × 10−19 | 1.19217704 × 10−13 | 6.32795333 × 10−16 |
| 0.5 | 4.44102736 × 10−16 | 3.44231543 × 10−18 | 4.55249634 × 10−13 | 1.46277017 × 10−14 |
| 0.6 | 6.39572035 × 10−16 | 1.01915459 × 10−17 | 1.73037412 × 10−12 | 3.31077250 × 10−13 |
| 0.7 | 8.70803912 × 10−16 | 2.53363580 × 10−17 | 1.65276878 × 10−8 | 6.40960986 × 10−9 |
| 0.8 | 1.13833300 × 10−15 | 5.52083544 × 10−17 | 1.76440709 × 10−4 | 6.86317136 × 10−5 |
| 0.9 | 1.44358770 × 10−15 | 1.08226613 × 10−16 | 0.61053707 | 0.23838980 |
| 1 | 1.78979417 × 10−15 | 1.93855241 × 10−16 | 863.820084 | 338.753375 |
| Ψ | ||||
|---|---|---|---|---|
| −20 | −1.10976051 × 10−17 | 1.63202785 × 10−14 | 1 | 1 |
| 20 | 2.79718628 × 10−16 | −1.33504319 × 10−14 | 1 | 1 |
| Ψ | ||||
|---|---|---|---|---|
| −20 | −7.85277215 × 10−17 | 1.67921232 × 10−15 | 1 | 1 |
| 20 | 1.77440778 × 10−17 | 3.02535774 × 10−15 | 1 | 1 |
| (0, α = 1.9) | (0, α = 1.9) | (0, α = 2) | (0, α = 2) |
|---|---|---|---|
| 0.881044762595 | 0.459213895856 | 0.894427190911 | 0.447213595446 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Arqub, O.A.; El-Ajou, A.; Al Zhour, Z.; Momani, S. Multiple Solutions of Nonlinear Boundary Value Problems of Fractional Order: A New Analytic Iterative Technique. Entropy 2014, 16, 471-493. https://doi.org/10.3390/e16010471
Arqub OA, El-Ajou A, Al Zhour Z, Momani S. Multiple Solutions of Nonlinear Boundary Value Problems of Fractional Order: A New Analytic Iterative Technique. Entropy. 2014; 16(1):471-493. https://doi.org/10.3390/e16010471
Chicago/Turabian StyleArqub, Omar Abu, Ahmad El-Ajou, Zeyad Al Zhour, and Shaher Momani. 2014. "Multiple Solutions of Nonlinear Boundary Value Problems of Fractional Order: A New Analytic Iterative Technique" Entropy 16, no. 1: 471-493. https://doi.org/10.3390/e16010471
APA StyleArqub, O. A., El-Ajou, A., Al Zhour, Z., & Momani, S. (2014). Multiple Solutions of Nonlinear Boundary Value Problems of Fractional Order: A New Analytic Iterative Technique. Entropy, 16(1), 471-493. https://doi.org/10.3390/e16010471






