Solutions of Some Nonlinear Diffusion Equations and Generalized Entropy Framework
Abstract
:1. Introduction
2. Nonlinear Diffusion Equation
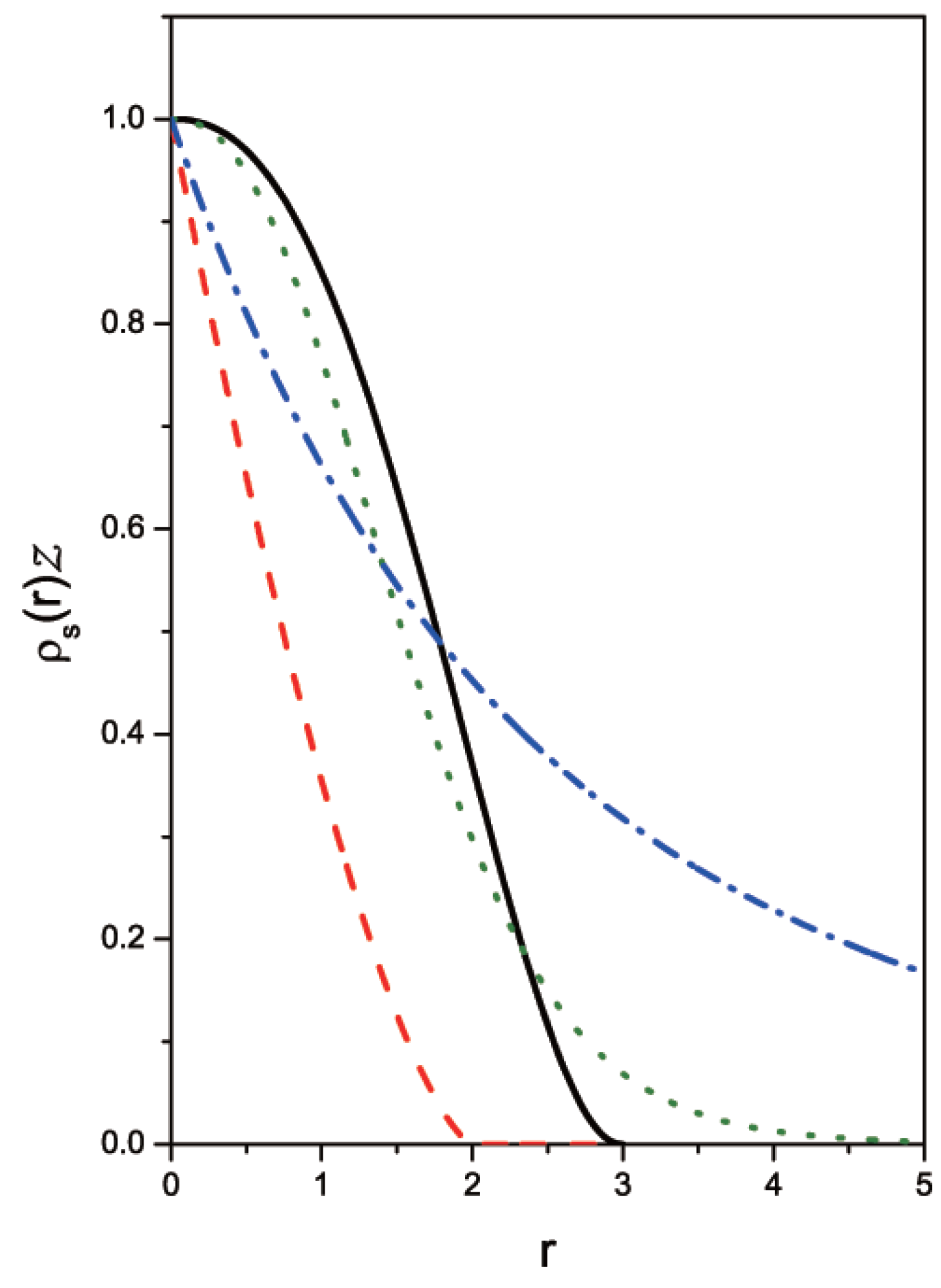
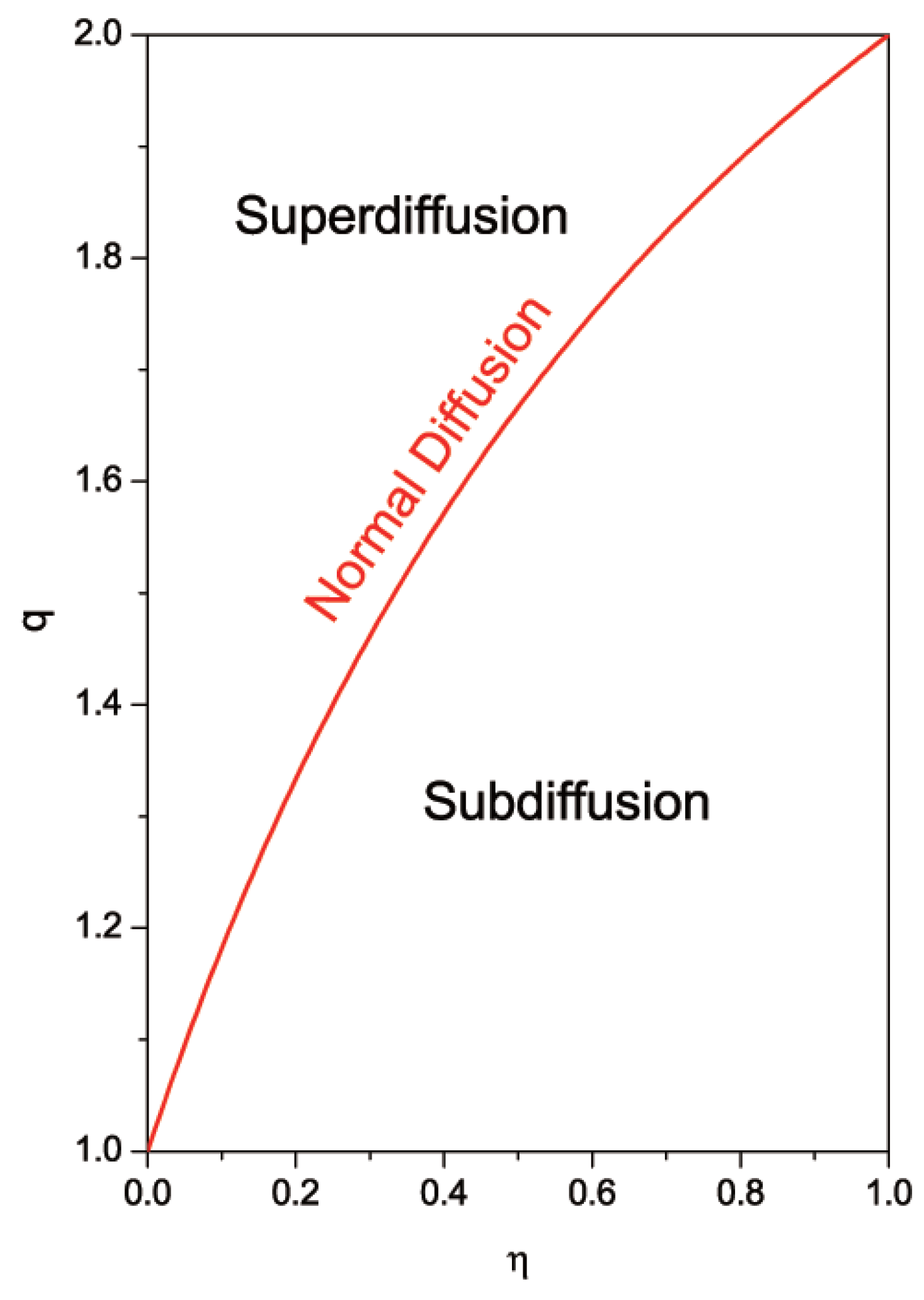
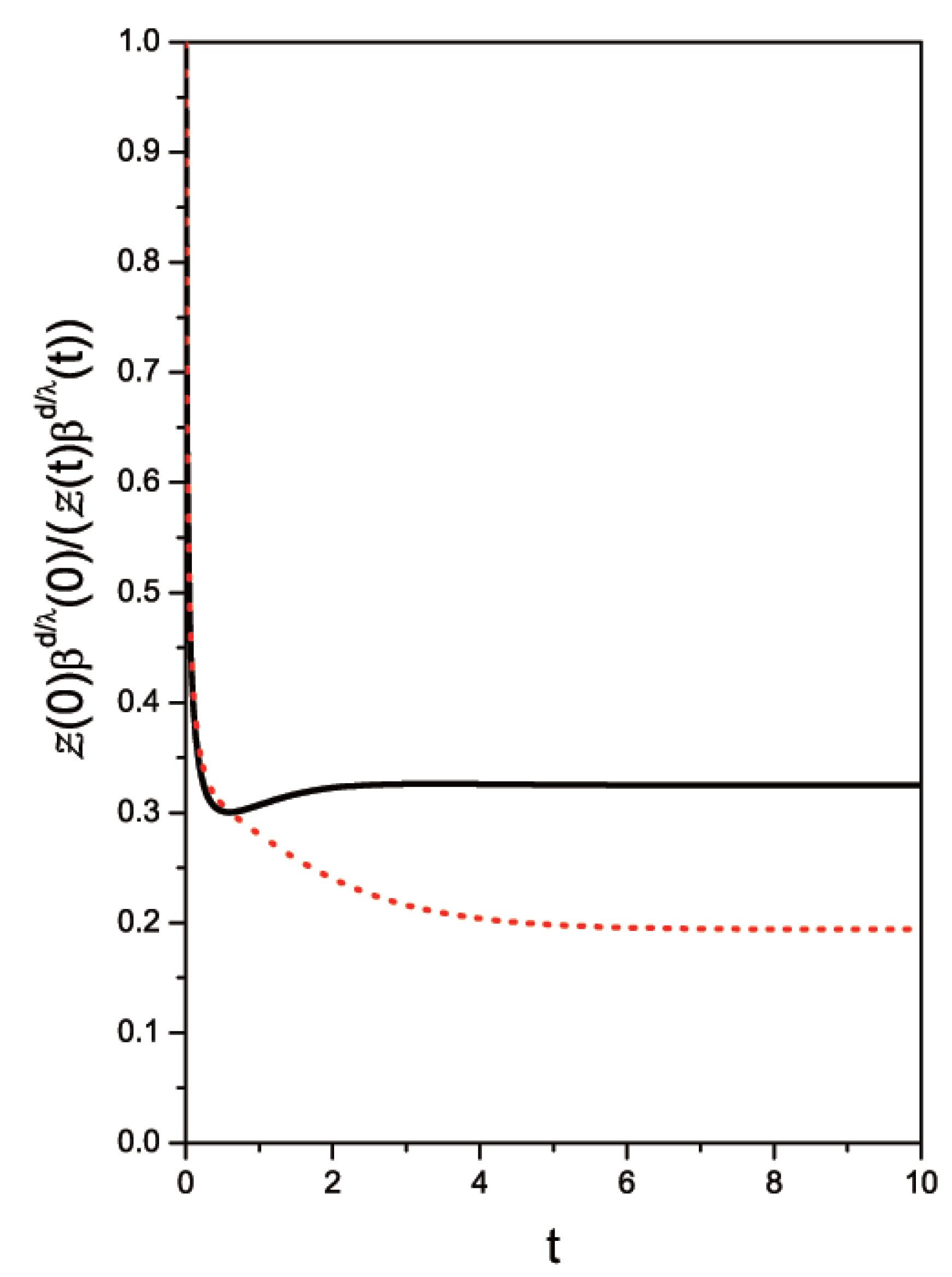
3. Summary and Conclusions
Acknowledgments
Conflicts of Interest
References
- Pekalski, A.; Sznajd-Weron, K. (Eds.) Anomalous Diffusion: From Basics to Applications; Lecture Notes in Physics; Springer: Berlin, Germany, 1999.
- Metzler, R.; Barkai, E.; Klafter, J. Anomalous transport in disordered systems under the influence of external fields. Physica A 1999, 266, 343–350. [Google Scholar] [CrossRef]
- Plotkin, S.S.; Wolynes, P.G. Non-Markovian configurational diffusion and reaction coordinates for protein folding. Phys. Rev. Lett. 1998, 80, 5015–5018. [Google Scholar] [CrossRef]
- Muskat, M. The Flow of Homogeneous Fluid Through Porous Media; McGraw-Hill: New York, NY, USA, 1937. [Google Scholar]
- Polubarinova-Kochina, P.Y. Theory of Ground Water Movement; Princeton University Press: Princeton, NJ, USA, 1962. [Google Scholar]
- Buckmaster, J. Viscous sheets advancing over dry bed. J. Fluid Mech. 1977, 81, 735–756. [Google Scholar] [CrossRef]
- Grosfils, P.; Boon, J.B. Nonextensive statistics in viscous fingering. Physica A 2006, 362, 168–173. [Google Scholar] [CrossRef]
- Andrade, J.S., Jr.; da Silva, G.F.T.; Moreira, A.A.; Nobre, F.D.; Curado, E.M.F. Thermostatistics of overdamped motion of interacting particles. Phys. Rev. Lett. 2010, 105, 260601. [Google Scholar] [CrossRef] [PubMed]
- Compte, A.; Jou, D.; Katayama, Y. Anomalous diffusion in linear shear flows. J. Phys. A 1997, 30, 1023–1030. [Google Scholar] [CrossRef]
- Giordano, C.; Plastino, A.R.; Casas, M.; Plastino, A. Anomalous diffusion in the presence of external forces: Exact time-dependent solutions and entropy. Eur. Phys. J. B 2001, 22, 361–368. [Google Scholar] [CrossRef]
- Tsallis, C.; Bukman, D.J. Anomalous diffusion in the presence of external forces: Exact time-dependent solutions and entropy. Phys. Rev. E 1996, 54, R2197–R2200. [Google Scholar] [CrossRef]
- Drazer, G.; Wio, H.S.; Tsallis, C. Anomalous diffusion with absorption: Exact time-dependent solutions. Phys. Rev. E 2000, 61, 1417–1422. [Google Scholar] [CrossRef]
- Curado, E.M.F.; Nobre, F.D. Derivation of nonlinear Fokker-Planck equations by means of approximations to the master equation. Phys. Rev. E 2003, 67, 021107. [Google Scholar] [CrossRef] [PubMed]
- Schwämmle, V.; Curado, E.M.F.; Nobre, F.D. Dynamics of normal and anomalous diffusion in nonlinear Fokker-Planck equations. Eur. Phys. J. B 2009, 70, 107–116. [Google Scholar] [CrossRef]
- Chavanis, P.H. Nonlinear mean-field Fokker-Planck equations and their applications in physics, astrophysics and biology. Phys. Rev. E 2003, 68, 036108. [Google Scholar] [CrossRef] [PubMed]
- Frank, T.D. On a general link between anomalous diffusion and nonextensivity. J. Math. Phys. 2002, 43, 344–350. [Google Scholar] [CrossRef]
- Plastino, A.R.; Plastino, A. Non-Extensive statistical mechanics and generalized Fokker-Planck equation. Physica A 1995, 222, 347–354. [Google Scholar] [CrossRef]
- Silva, P.C.; da Silva, L.R.; Lenzi, E.K.; Mendes, R.S.; Malacarne, L.C. Nonlinear diffusion equation, Tsallis formalism and exact solutions. Physica A 2004, 342, 16–19. [Google Scholar]
- Plastino, A.R.; Casas, M.; Plastino, A. A nonextensive maximum entropy approach to a family of nonlinear reaction-diffusion equations. Physica A 2000, 280, 289–303. [Google Scholar] [CrossRef]
- Wada, T.; Scarfone, A.M. On the non-linear Fokker-Planck equation associated with κ-entropy. AIP Conf. Proc. 2007, 965, 177–180. [Google Scholar]
- Wada, T.; Scarfone, A.M. Asymptotic solutions of a nonlinear diffusive equation in the framework of κ-generalized statistical mechanics. Eur. Phys. J. B 2009, 70, 65–71. [Google Scholar] [CrossRef]
- Frank, T.D. Nonlinear Fokker-Planck Equations; Springer: Heidelberg, Germany, 2005. [Google Scholar]
- Reisner, J.; Serencsa, J.; Shkoller, S. A spacetime smooth artificial viscosity method for nonlinear conservation laws. J. Comput. Phys. 2013, 235, 912–933. [Google Scholar] [CrossRef]
- Tsallis, C.; Plastino, A.R.; Mendes, R.S. The role of constraints within generalized nonextensive statistics. Physica A 1998, 261, 534–554. [Google Scholar] [CrossRef]
- Coffey, W.T.; Kalmykov, Y.P.; Waldron, J.T. The Langevin Equation: With Applications to Stochastic Problems in Physics, Chemistry and Electrical Engineering; World Scientific Publishing Company: Singapore, Singapore, 2004. [Google Scholar]
- Sandev, T.; Metzler, R.; Tomovski, Z. Velocity and displacement correlation functions for fractional generalized Langevin equations. Fract. Calc. Appl. Anal. 2012, 15, 426–450. [Google Scholar] [CrossRef]
- Weiss, G.W. Aspects and Applications of the Random Walk; North Holland: Amesterdan, The Netherlands, 1994. [Google Scholar]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, Singapore, 2000. [Google Scholar]
- Priya, G.S.; Prakash, P.; Nieto, J.J.; Kayar, Z. Higher-order numerical scheme for the fractional heat equation with dirichlet and neumann boundary conditions. Numer. Heat Transf. Part B 2013, 63, 540–559. [Google Scholar] [CrossRef]
- Tomovski, Z.; Sandev, T.; Metzler, R.; Dubbeldam, J. Generalized space-time fractional diffusion equation with composite fractional time derivative. Physica A 2012, 391, 2527–2542. [Google Scholar] [CrossRef]
- Silva, A.T.; Lenzi, E.K.; Evangelista, L.R.; Lenzi, M.K.; da Silva, L.R. Fractional nonlinear diffusion equation, solutions and anomalous diffusion. Physica A 2007, 375, 65–71. [Google Scholar] [CrossRef]
- Alibaud, N.; Cifani, S.; Jakobsen, E.R. Continuous dependence estimates for nonlinear fractional convection-diffusion equations. SIAM J. Math. Anal. 2012, 44, 603–632. [Google Scholar] [CrossRef]
- Cifani, S.; Jakobsen, E.R.; Karlsen, K.H. The discontinuous Galerkin method for fractional degenerate convection-diffusion equations. BIT Numer. Math. 2011, 51, 809–844. [Google Scholar] [CrossRef]
- Pascal, H. A nonlinear model of heat conduction. J. Phys. A 1992, 25, 939–948. [Google Scholar] [CrossRef]
- Daly, E.; Porporato, A. Similarity solutions of nonlinear diffusion problems related to mathematical hydraulics and the Fokker-Planck equation. Phys. Rev. E 2004, 70, 056303. [Google Scholar] [CrossRef] [PubMed]
- Gratton, J.; Minotti, F.; Mahajan, S.M. Theory of creeping gravity currents of a non-Newtonian liquid. Phys. Rev. E 1999, 60, 6960–6967. [Google Scholar] [CrossRef]
- Troncoso, P.; Fierro, O.; Curilef, S.; Plastino, A.R. A family of evolution equations with nonlinear diffusion, Verhulst growth, and global regulation: Exact time-dependent solutions. Physica A 2007, 375, 457–466. [Google Scholar] [CrossRef]
- Tsallis, C.; Levy, S.V.F.; Souza, A.M.C.; Maynard, R. Statistical mechanical foundation of the ubiquity of Lvy distributions in nature. Phys. Rev. Lett. 1995, 75, 3589–3782. [Google Scholar] [CrossRef] [PubMed]
- Tsallis, C.; Levy, S.V.F.; Souza, A.M.C.; Maynard, R. Errata: Statistical mechanical foundation of the ubiquity of Lvy distributions in nature [Phys. Rev. Lett. 75, 3589 (1995)]. Phys. Rev. Lett. 1996, 77, 5442. [Google Scholar] [CrossRef]
- Prato, D.; Tsallis, C. Nonextensive foundation of Levy distributions. Phys. Rev. E 2000, 60, 2398–2400. [Google Scholar] [CrossRef]
- Murray, J. Mathematical Biology; Springer: Berlin, Germany, 1989. [Google Scholar]
- Verhulst, P.F. Recherches mathematiques sur la loi daccroissement de la population. Mem. Acad. R. Belg. 1845, 18, 1–38. (in French). [Google Scholar]
- Mazumdar, J. An Introduction to Mathematical Physiology and Biology; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Hutchinson, G.E. An Introduction to Population Ecology; Yale University Press: New Haven, CT, USA, 1978. [Google Scholar]
- Leach, P.G.L.; Andriopoulos, K. An oscillatory population model. Chaos Soliton. Fract. 2004, 22, 1183–1188. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lenzi, E.K.; Dos Santos, M.A.F.; Michels, F.S.; Mendes, R.S.; Evangelista, L.R. Solutions of Some Nonlinear Diffusion Equations and Generalized Entropy Framework. Entropy 2013, 15, 3931-3940. https://doi.org/10.3390/e15093931
Lenzi EK, Dos Santos MAF, Michels FS, Mendes RS, Evangelista LR. Solutions of Some Nonlinear Diffusion Equations and Generalized Entropy Framework. Entropy. 2013; 15(9):3931-3940. https://doi.org/10.3390/e15093931
Chicago/Turabian StyleLenzi, Ervin K., Maike A. F. Dos Santos, Flavio S. Michels, Renio S. Mendes, and Luiz R. Evangelista. 2013. "Solutions of Some Nonlinear Diffusion Equations and Generalized Entropy Framework" Entropy 15, no. 9: 3931-3940. https://doi.org/10.3390/e15093931
APA StyleLenzi, E. K., Dos Santos, M. A. F., Michels, F. S., Mendes, R. S., & Evangelista, L. R. (2013). Solutions of Some Nonlinear Diffusion Equations and Generalized Entropy Framework. Entropy, 15(9), 3931-3940. https://doi.org/10.3390/e15093931




