1. Introduction
The relative entropy between two probability distributions has many applications in classical and quantum information theory. A number of these applications, including the conditional limit theorem [
1], quantum error correction [
2], and secure random number generation and communication [
3,
4], make use of lower bounds on the relative entropy in terms of a suitable distance between the two distributions. The best known such bound is the so-called Pinsker inequality [
5]
where
is the variational or L1 distance between distributions
P and
Q. Note that the choice of logarithm base is left open throughout this paper, corresponding to a choice of units. There are a number of such bounds [
5], all of which easily generalise to the case of quantum probabilities [
2,
6,
7].
However, in a number of applications of the Pinsker inequality and its quantum analog, a lower bound is in fact only needed for the special case that the relative entropy quantifies the mutual information between two systems. Such applications include, for example, secure random number generation and coding [
3,
4] (both classical and quantum), and quantum de Finnetti theorems [
8]. Since mutual information is a special case of relative entropy, it follows that it may be possible to find strictly stronger lower bounds for mutual information.
Surprisingly little attention appears to have been paid to this possibility of better lower bounds (although upper bounds for mutual information have been investigated [
9]). The results of preliminary investigations are given here, with explicit tight lower bounds being obtained for pairs of two-valued classical random variables, and for pairs of quantum qubits with maximally-mixed reduced states.
In the context of mutual information, the corresponding variational distance reduces to the distance between the joint state of the systems and the product of their marginal states, referred to here as the “correlation distance”. It is shown that both the classical and quantum correlation distances are relevant for quantifying properties of quantum entanglement: the former with respect to the classical resources required to simulate entanglement, and the latter as providing a criterion for qubit entanglement. In the quantum case, it is also shown that the minimum value of the mutual information can only be achieved by entangled qubits if the correlation distance is more than ≈.
The main results are given in the following section. Lower bounds on classical and quantum mutual information for two-level systems are derived in
Section 3 and
Section 5, and an entanglement criterion for qubits in terms of the quantum correlation distance is obtained in
Section 4. Connections with classically-correlated quantum states are briefly discussed in
Section 6, and conclusions are presented in
Section 7.
2. Definitions and Main Results
For two classical random variables
A and
B, with joint probability distribution
and marginal distributions
and
, the Shannon mutual information and the classical correlation distance are defined respectively by
where
denotes the Shannon entropy of distribution
P. The term “correlation distance” is used for
, since it inherits all the properties of a distance from the more general variational distance, and clearly vanishes for uncorrelated
A and
B. Both the mutual information and correlation distance have a minimum value of zero, and for
n-valued random variables have maximum values
with saturation corresponding to the maximally correlated case
. Note for
that
.
For two quantum systems
A and
B described by density operator
and reduced density operators
and
, the corresponding quantum mutual information and quantum correlation distance are analogously defined by
where
denotes the von Neumann entropy of density operator
ρ. Similarly to the classical case, these are direct measures of the correlation between
A and
B, vanishing only for uncorrelated
A and
B. It may be noted that trace distance has recently also been used to distinguish between and quantify quantum and classical contributions to this correlation [
10,
11]. For
n-level quantum systems one has the maximum values
with saturation corresponding to maximally entangled states. Thus, comparing with Equation (
4), quantum correlations have a quadratic advantage with respect to both mutual information and correlation distance. For example, for
one has
, allowing quantum correlation distances that are greater than the corresponding classical maximum value of unity.
In both the classical and quantum cases, one has the lower bound
for mutual information, as a direct consequence of the Pinsker inequality (
1) for classical relative entropies [
2,
5,
6,
7]. However, better bounds for mutual information can be obtained, which are stronger than any general inequality for relative entropy and variational distance.
For example, for two-valued classical random variables
A and
B one has the tight lower bound
for classical mutual information. This inequality has been previously stated without proof in Reference [
12], where it was used to bound the shared information required to classically simulate entangled quantum systems. It is proved in
Section 3 below.
In contrast to Pinsker-type inequalities such as Equation (
8), the quantum generalisation of Equation (
9) is not straightforward. In particular, note for a two-qubit system that one cannot simply replace
by
in Equation (
9), as the right hand side would be undefined for
. This can occur if the qubits are entangled. Indeed, as shown in
Section 4,
is a sufficient condition for the entanglement of two qubits, as is the stronger condition
An explicit expression for the quantum correlation distance for two qubits, in terms of the spin covariance matrix, is also given in
Section 4.
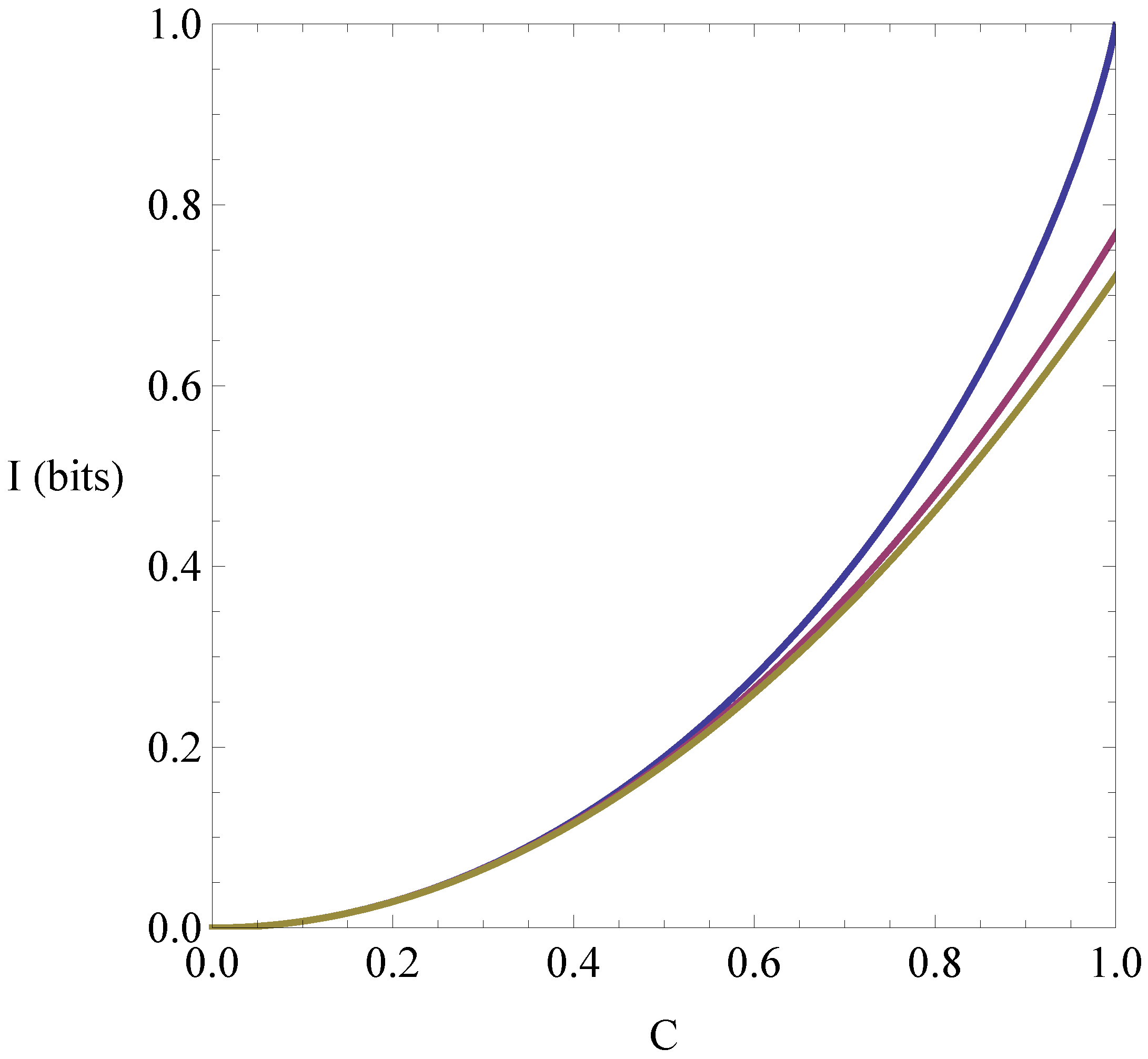
It is shown in
Section 5 that the quantum equivalent of Equation (
9),
i.e., a tight lower bound for the quantum mutual information shared by two qubits, is
when the reduced density operators are maximally mixed, where
corresponds to the value of
for which the two expressions are equal. For
this lower bound can only be achieved by entangled states, and cannot be achieved by any classical distribution
having the same correlation distance. It is also shown that, for
, the bound is also tight if only one of the reduced states is maximally mixed. Support is given for the conjecture that the bound in Equation (
11) in fact holds for all two-qubit states.
In
Section 6 the natural role of “classically-correlated” quantum states, in comparing classical and quantum correlations, is briefly discussed. Such states have the general form
[
13], where
is a classical joint probability distribution and
and
are orthonormal basis sets for the two quantum systems. The lower bound in Equation (
11) can be saturated by a classically-correlated state if and only if
.
6. Classically-Correlated Quantum States
It is well known that a quantum system behaves classically if the state and the observables of interest all commute,
i.e., if they can be simultaneously diagonalised in some basis. Hence, a joint state will behave classically if the relevant observables of each system commute with each other and the state. It is therefore natural to define
to be
classically correlated if and only if it can be diagonalised in a joint basis [
13],
i.e., if and only if
for some distribution
and orthonormal basis set
. Classical correlation is preserved by tensor products, and by mixtures of commuting states.
While, strictly speaking, a classically-correlated quantum state only behaves classically with respect to observables that are diagonal with respect to
, they also have a number of classical correlation properties with respect to general observables [
13,
22], briefly noted here.
First,
above is separable by construction, and hence is unentangled. Second, since it is diagonal in the basis
, the mutual information and correlation distance are easily calculated as
and hence can only take classical values.
Third, if
M and
N denote any observables for systems
A and
B respectively, then their joint statistics are given by
where
is a stochastic matrix with respect to its first and second pairs of indices. Similarly, one finds
for the product of the marginals. Since the classical relative entropy and variational distance can only decrease under the action of a stochastic matrix, it follows that one has the tight inequalities [
13,
22]
with saturation for
M and
N diagonal in the bases
and
respectively. Maximising the first of these equalities over
M or
N immediately implies the well-known result that classically-correlated states have zero quantum discord [
22].
Finally, for two-qubit systems, Equation (
52) implies that
is classically correlated if and only if it is equivalent under local unitary transformations to a state of the form
where
and
r satisfies Equation (
12). Hence, the mutual information is bounded by the classical lower bound in Equation (
9), and
in Equation (
43) is classically correlated for
. It follows that the lower bound for quantum mutual information in Equation (
11) can be attained by classically-correlated states if
. Conversely, the minimum possible bound cannot be reached by any classically-correlated two-qubit state if
.
7. Conclusions
Lower bounds for mutual information have been obtained that are stronger than those obtainable from general bounds for relative entropy and variational distance. Unlike the Pinsker inequality in Equation (
8), the quantum form of these bounds is not a simple generalisation of the classical form.
Similarly to the case of upper bounds for (classical) mutual information [
9], the tight lower bounds obtained here depend on the dimension of the systems. The results of this paper represent a preliminary investigation largely confined to two-valued classical variables and qubits. It would be of interest to generalise both the classical and quantum cases, and to further investigate connections between them.
Open questions include whether a quantum correlation distance greater than the corresponding maximum classical correlation distance is a signature of entanglement for higher-dimensional systems, and whether the related qubit entanglement criterion in Equation (
10) holds more generally. The conjecture in
Section 5.2, as to whether the quantum lower bound in Equation (
11) is valid for all two-qubit states, also remains to be settled. Finally, it would be of interest to generalise and to better understand the role of the transition from classically-correlated states to entangled states in saturating information bounds, in the light of Equation (
43) for qubits.