Non-Linear Canonical Correlation Analysis Using Alpha-Beta Divergence
Abstract
:1. Introduction
2. Canonical Correlation Analysis
3. AB-Divergence
4. AB-Canonical Analysis
5. ABCA Algorithm
6. Sequential Permutation Test
7. Extension to Tensor
8. Sparseness Constraints
9. Simulation Results
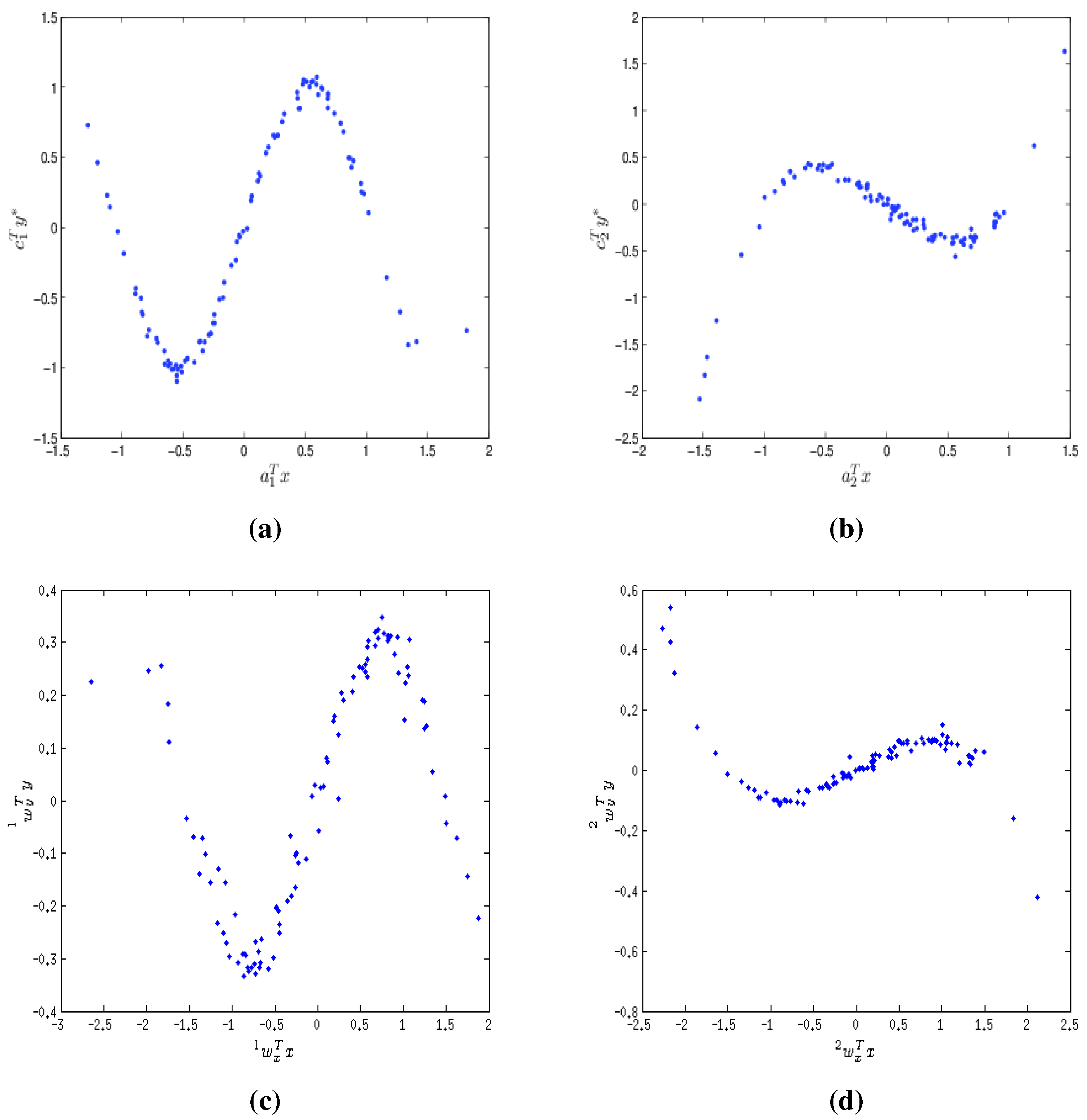
9.1. Extraction of Non-linear Relationship
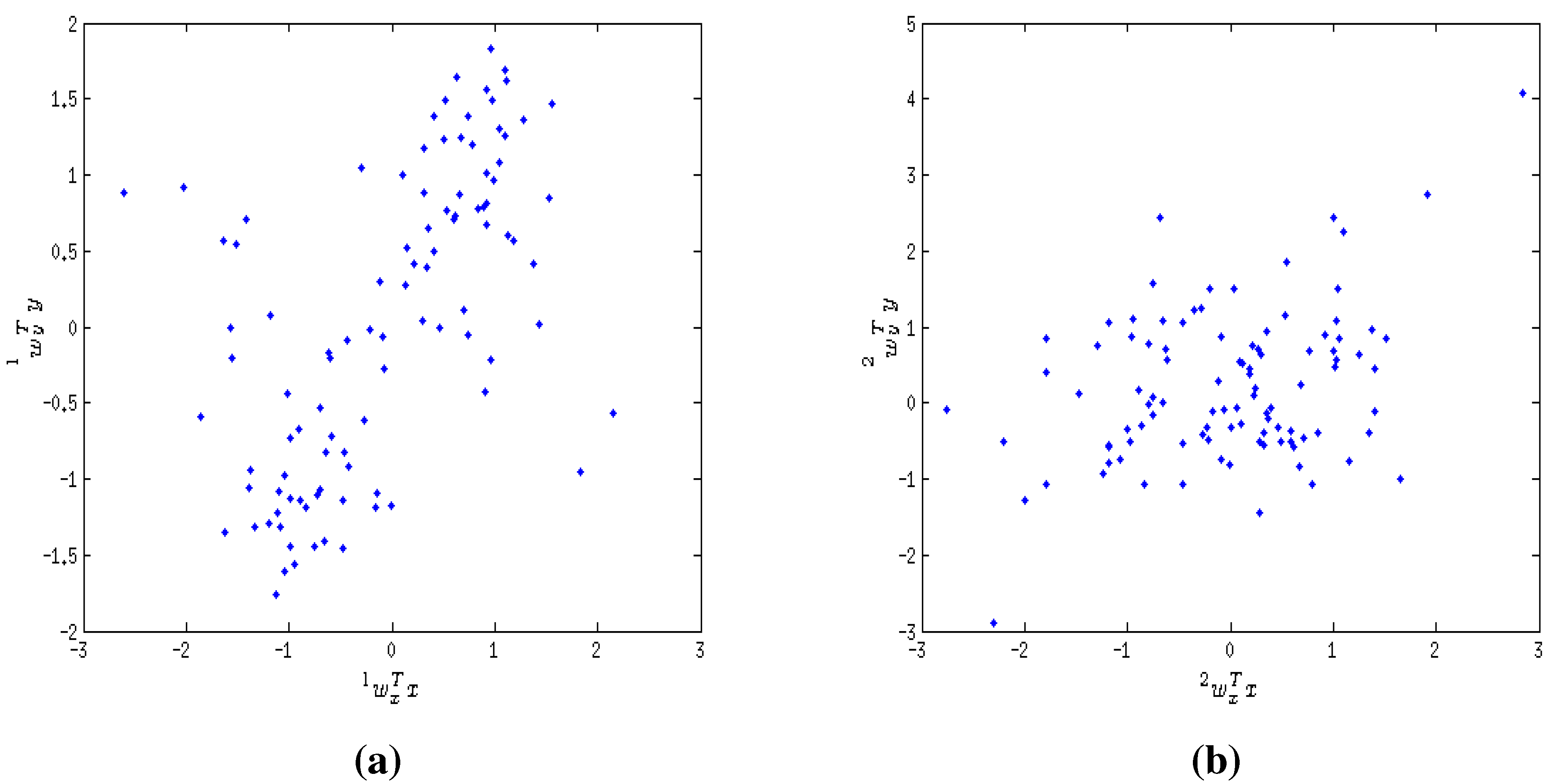

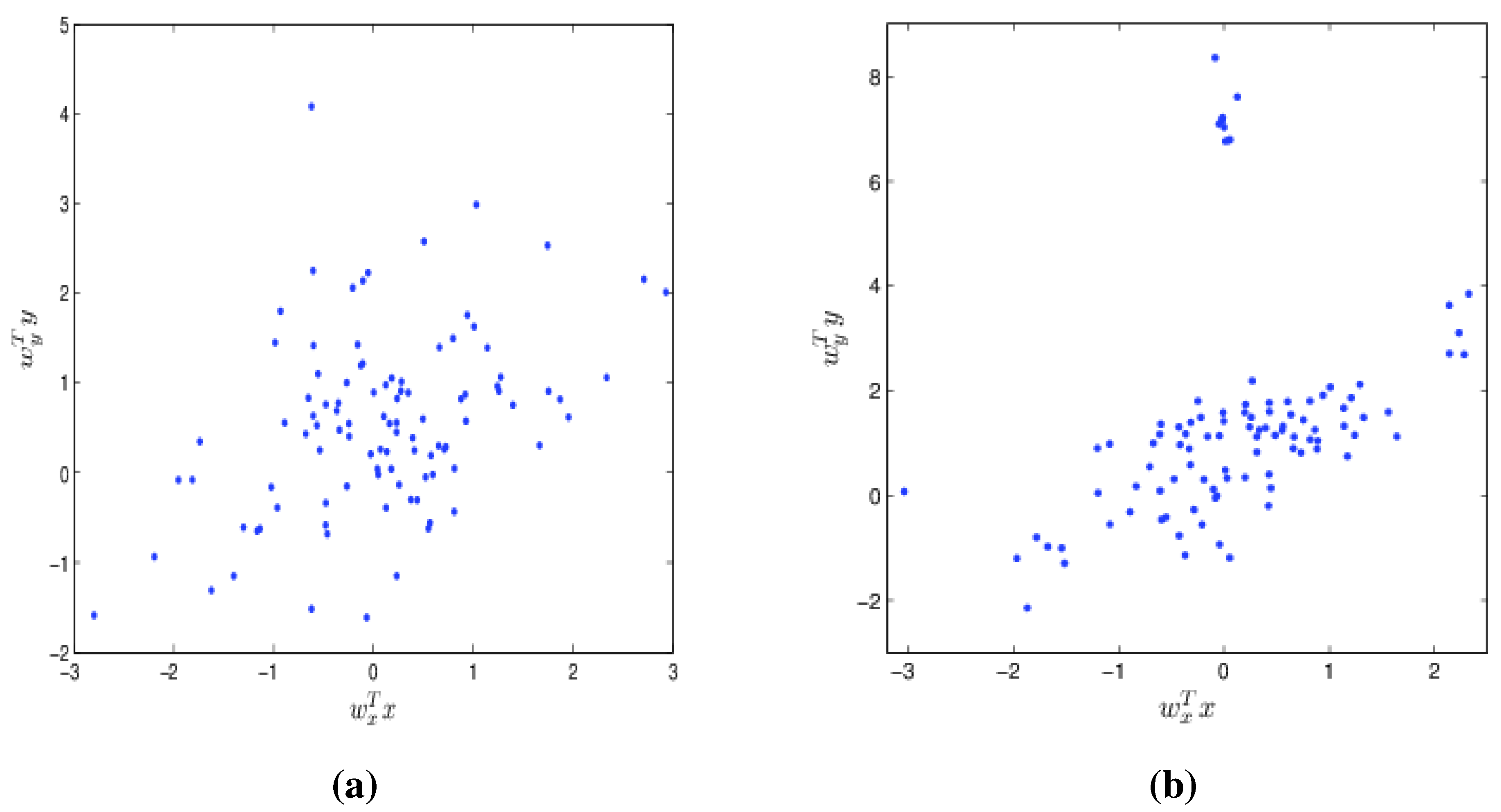
9.2. Robustness Property
9.3. Tensor Data
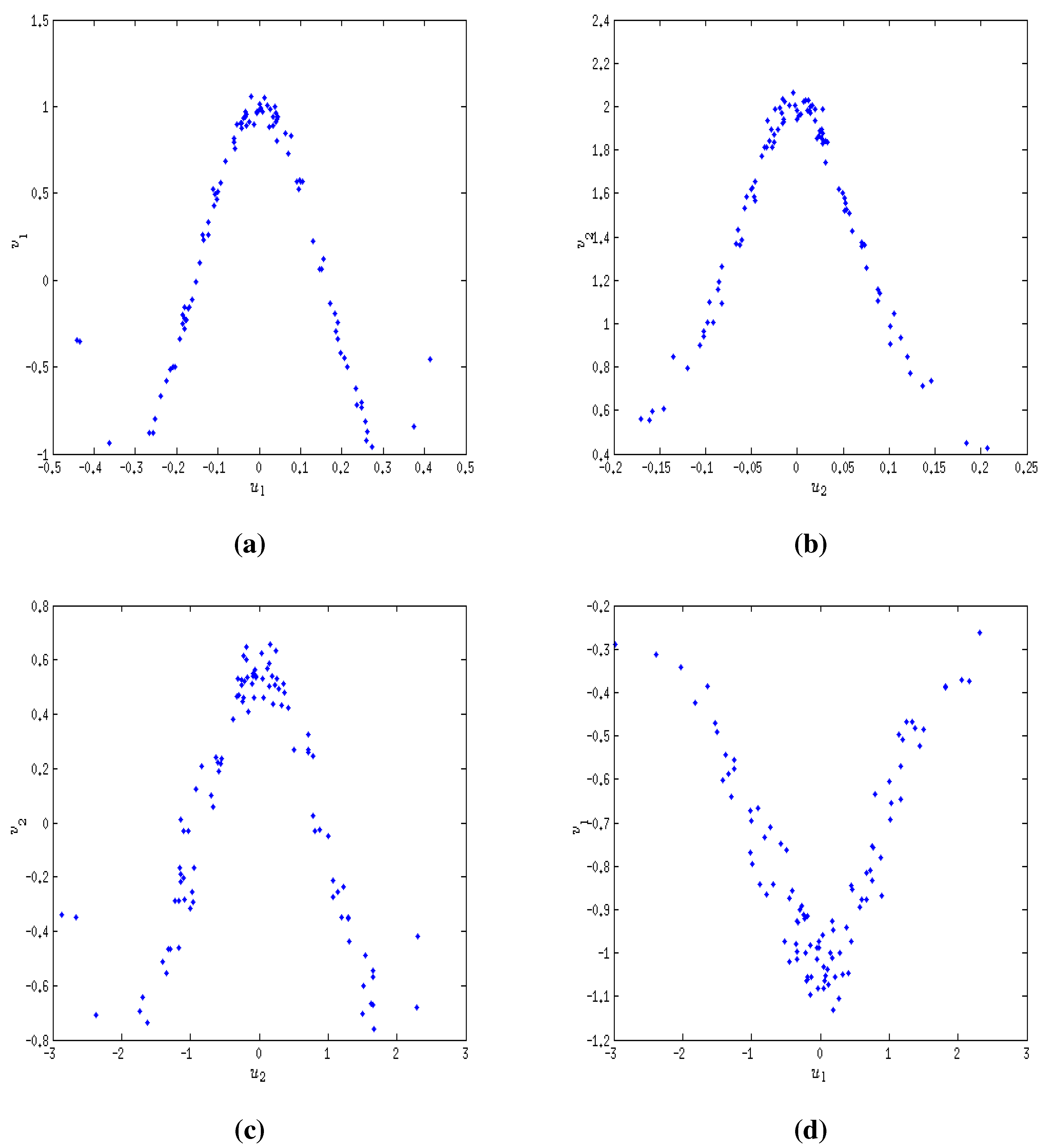
9.4. Choice of Divergence Parameters
10. Conclusion
Acknowledgements
Conflict of Interest
References
- Yin, X. Canonical correlation analysis based on information theory. J. Multivar. Anal. 2004, 91, 161–176. [Google Scholar] [CrossRef]
- Yin, X.; Sriram, T. Common canonical variates for independent groups using information theory. Stat. Sin. 2008, 18, 335–353. [Google Scholar]
- Iaci, R.; Sriram, T.; Yin, X. Multivariate association and dimension reduction: A generalization of canonical correlation analysis. Biometrics 2010, 66, 1107–1118. [Google Scholar] [CrossRef] [PubMed]
- Iaci, R.; Sriram, T. Robust multivariate association and dimension reduction using density divergences. J. Multivar. Anal. 2013, 117, 281–295. [Google Scholar] [CrossRef]
- Wang, X.; Crowe, M.; Fyfe, C. Dual stream data exploration. Int. J. Data Min., Model. Manage. 2012, 4, 188–202. [Google Scholar] [CrossRef]
- Cichocki, A.; Cruces, S.; Amari, S.I. Generalized alpha-beta divergences and their application to robust nonnegative matrix factorization. Entropy 2011, 13, 134–170. [Google Scholar] [CrossRef]
- Lai, P.L.; Fyfe, C. Kernel and nonlinear canonical correlation analysis. Int. J. Neural Syst. 2000, 10, 365–377. [Google Scholar] [CrossRef] [PubMed]
- Shawe-Taylor, J.; Cristianini, N. Kernel Methods for Pattern Analysis; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Breiman, L.; Friedman, J.H. Estimating optimal transformations for multiple regression and correlation. J. Am. Stat. Assoc. 1985, 80, 580–598. [Google Scholar] [CrossRef]
- Hotelling, H. Relations between two sets of variates. Biometrika 1936, 28, 321–377. [Google Scholar] [CrossRef]
- Amari, S.I. Integration of stochastic models by minimizing α-divergence. Neural Comput. 2007, 19, 2780–2796. [Google Scholar] [CrossRef] [PubMed]
- Mihoko, M.; Eguchi, S. Robust blind source separation by beta divergence. Neural comput. 2002, 14, 1859–1886. [Google Scholar] [CrossRef] [PubMed]
- Basu, A.; Harris, I.R.; Hjort, N.L.; Jones, M. Robust and efficient estimation by minimising a density power divergence. Biometrika 1998, 85, 549–559. [Google Scholar] [CrossRef]
- Cichocki, A.; Zdunek, R.; Amari, S.I. Csiszár’s divergences for non-negative matrix factorization: Family of new algorithms. In Independent Component Analysis and Blind Signal Separation, Proceedings of Fifth International Conference, ICA 2004, Granada, Spain, 22–24 September 2004; Puntonet, C.G., Prieto, A., Eds.; Springer: Berlin, Heidelberg, Germany, 2006; pp. 32–39. [Google Scholar]
- Kompass, R. A generalized divergence measure for nonnegative matrix factorization. Neural comput. 2007, 19, 780–791. [Google Scholar] [CrossRef] [PubMed]
- Févotte, C.; Bertin, N.; Durrieu, J.L. Nonnegative matrix factorization with the Itakura-Saito divergence with application to music analysis. Neural Comput. 2009, 21, 793–830. [Google Scholar] [CrossRef] [PubMed]
- Scott, D.W. Multivariate Density Estimation: Theory, Practice, and Visualization; Wiley: New York, NY, USA, 1992; Volume 1. [Google Scholar]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; Chapman & Hall/CRC: London, UK, 1986; Volume 26. [Google Scholar]
- Kim, J.S.; Scott, C. Robust kernel density estimation. J. Mach. Learn. Res. 2012, 13, 2529–2565. [Google Scholar]
- Byrd, R.H.; Hribar, M.E.; Nocedal, J. An interior point algorithm for large-scale nonlinear programming. SIAM J. Optim. 1999, 9, 877–900. [Google Scholar] [CrossRef]
- Byrd, R.H.; Gilbert, J.C.; Nocedal, J. A trust region method based on interior point techniques for nonlinear programming. Math. Program. 2000, 89, 149–185. [Google Scholar] [CrossRef]
- MATLAB code of ABCA. Available online: http://www.isical.ac.in/∼abhijit_v/ABC.m (accessed on 17 July 2013).
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Chapman & Hall/CRC: New York, NY, USA, 1993; Volume 57. [Google Scholar]
- Davison, A.C.; Hinkley, D.V. Bootstrap Methods and Their Application; Cambridge University Press: Cambridge, UK, 1997; Volume 1. [Google Scholar]
- Kolda, T.G.; Bader, B.W. Tensor decompositions and applications. SIAM rev. 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Cichocki, A.; Zdunek, R.; Phan, A.H.; Amari, S.I. Nonnegative Matrix and Tensor Factorizations: Applications to Exploratory Multi-way Data Analysis and Blind Source Separation; Wiley: Chichester, UK, 2009. [Google Scholar]
- Torres, D.A.; Turnbull, D.; Barrington, L.; Lanckriet, G.R. Identifying words that are musically meaningful. In Proceedings of the 8th International Conference of Music Information Retrieval, Vienna, Austria, 23–27 September 2007; Volume 7, pp. 405–410.
- Witten, D.M.; Tibshirani, R.; Hastie, T. A penalized matrix decomposition, with applications to sparse principal components and canonical correlation analysis. Biostatistics 2009, 10, 515–534. [Google Scholar] [CrossRef] [PubMed]
- Witten, D.M. A penalized matrix decomposition, and its applications. PhD thesis, Stanford University, USA, 2010. [Google Scholar]
- Allen, G.I. Sparse higher-order principal components analysis. In Proceedings of 15th International Conference on Artificial Intelligence and Statistics, Canary Islands, Spain, 20–22 April 2012; Volume 22, pp. 27–36.
- Scott, D.W. Parametric statistical modeling by minimum integrated square error. Technometrics 2001, 43, 274–285. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Mandal, A.; Cichocki, A. Non-Linear Canonical Correlation Analysis Using Alpha-Beta Divergence. Entropy 2013, 15, 2788-2804. https://doi.org/10.3390/e15072788
Mandal A, Cichocki A. Non-Linear Canonical Correlation Analysis Using Alpha-Beta Divergence. Entropy. 2013; 15(7):2788-2804. https://doi.org/10.3390/e15072788
Chicago/Turabian StyleMandal, Abhijit, and Andrzej Cichocki. 2013. "Non-Linear Canonical Correlation Analysis Using Alpha-Beta Divergence" Entropy 15, no. 7: 2788-2804. https://doi.org/10.3390/e15072788
APA StyleMandal, A., & Cichocki, A. (2013). Non-Linear Canonical Correlation Analysis Using Alpha-Beta Divergence. Entropy, 15(7), 2788-2804. https://doi.org/10.3390/e15072788



