Effect of Prey Refuge on the Spatiotemporal Dynamics of a Modified Leslie-Gower Predator-Prey System with Holling Type III Schemes
Abstract
:1. Introduction
2. Existence of Global Solutions and Permanence
2.1. Existence of Global Solutions
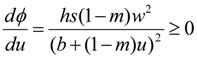
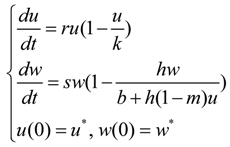
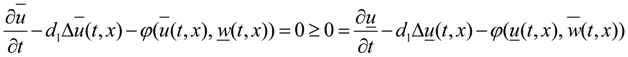
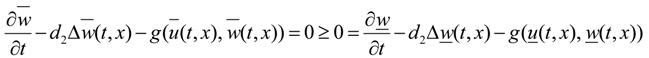
2.2. Permanence
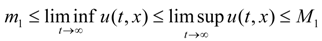
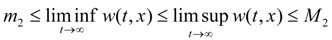
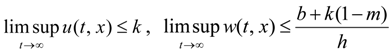
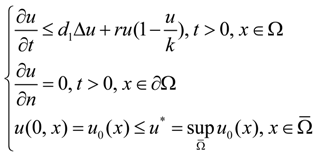
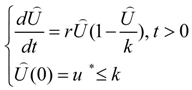
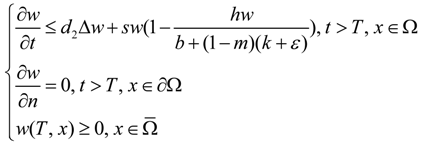

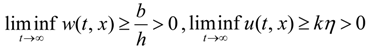
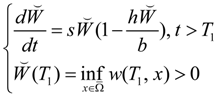
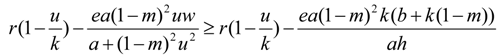
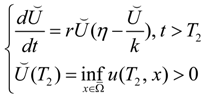
3. Stability Analysis of Equilibrium Points and Turing Instability
3.1. Stability
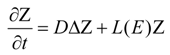
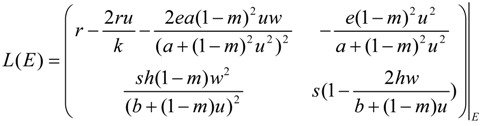
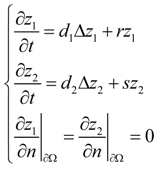
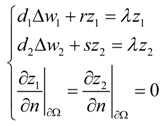
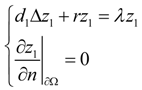
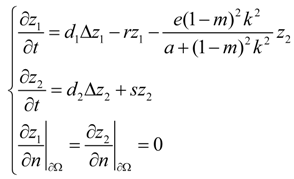
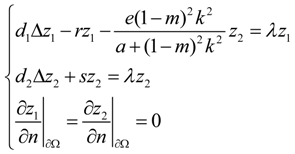
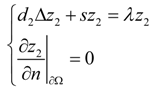
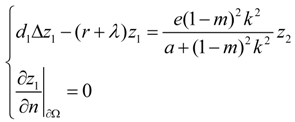
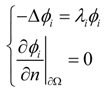

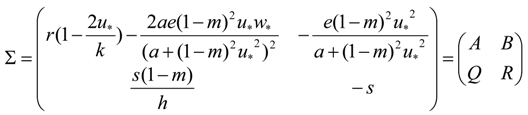
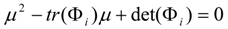
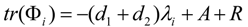

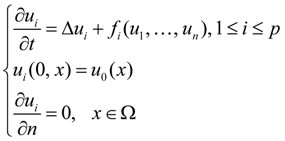
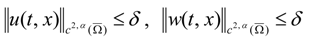
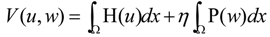
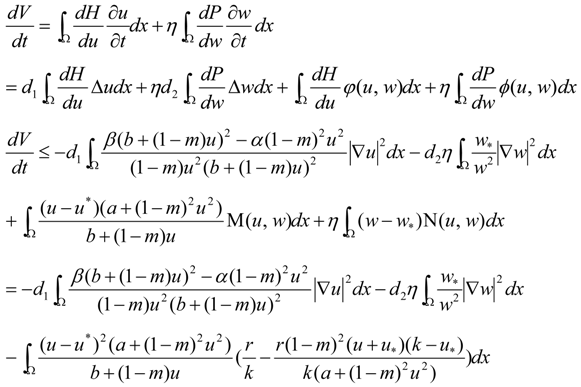
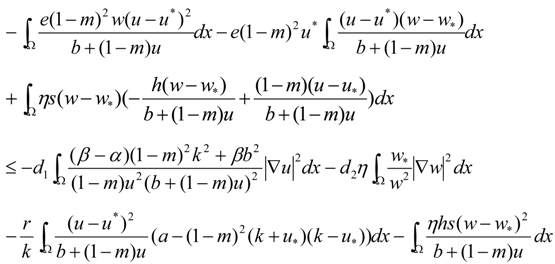
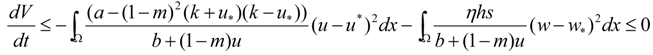
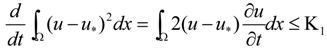
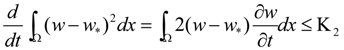
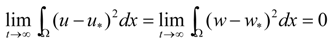
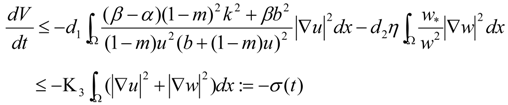
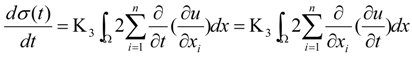
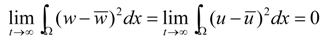
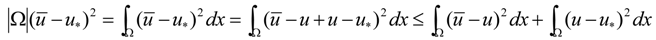
3.2. Turing Instability
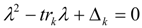
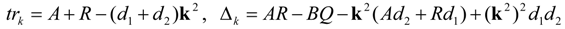
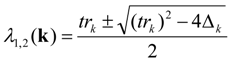
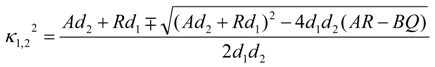
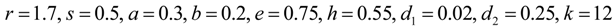
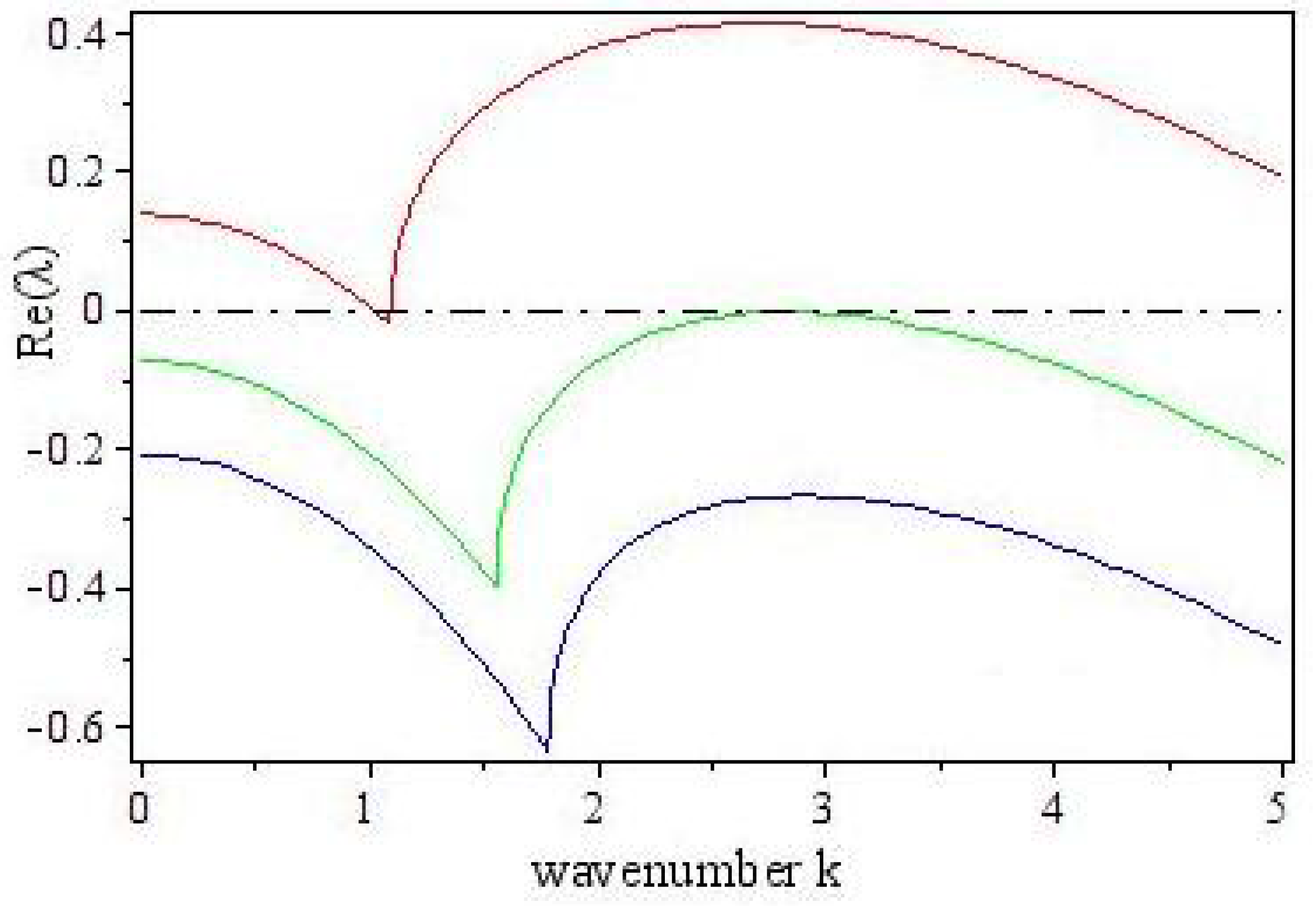
4. Turing Pattern Formation
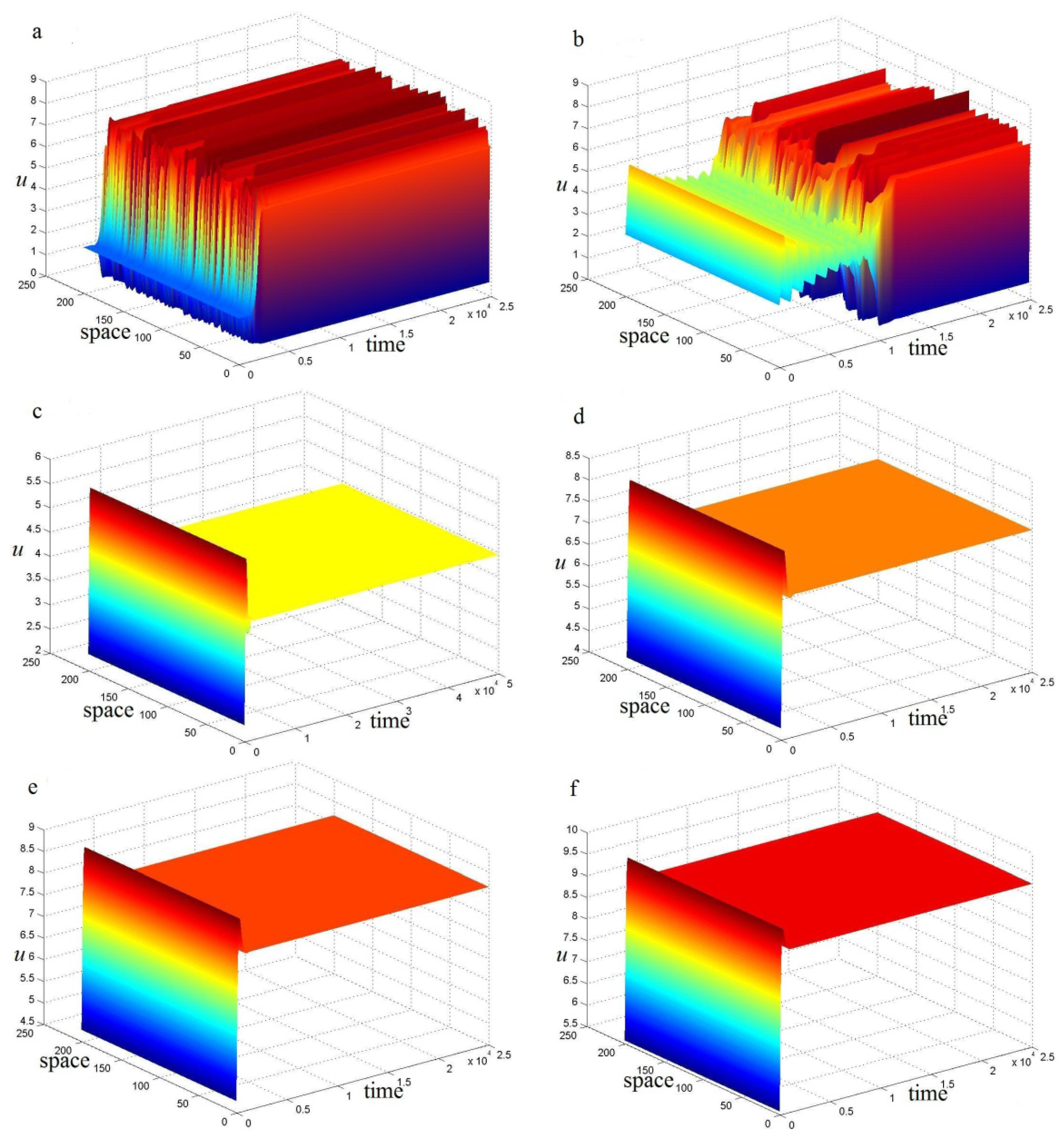
5. Conclusions
Acknowledgments
Conflict of Interest
References
- Baek, H. A food chain system with Holling type IV functional response and impulsive perturbations. Comput. Math. Appl. 2010, 60, 1152–1163. [Google Scholar] [CrossRef]
- Zhao, M.; Lv, S.J. Chaos in a three-species food chain model with a Beddington-DeAngelis functional response. Chaos Soliton. Fract. 2009, 40, 2305–2316. [Google Scholar] [CrossRef]
- González-Olivares, E.; González-Yañez, B.; Lorca, J.M.; Rojas-Palma, A.; Flores, J.D. Consequences of double Allee effect on the number of limit cycles in a predator–prey model. Comput. Math. Appl. 2011, 62, 3449–3463. [Google Scholar] [CrossRef]
- Yu, H.G.; Zhong, S.M.; Agarwal, R.P.; Xiong, L.L. Species permanence and dynamical behavior analysis of an impulsively controlled ecological system with distributed time delay. Comput. Math. Appl. 2010, 59, 382–3835. [Google Scholar] [CrossRef]
- Zhao, M.; Wang, X.T.; Yu, H.G.; Zhu, J. Dynamics of an ecological model with impulsive control strategy and distributed time delay. Math. Comput. Simul. 2012, 82, 1432–1444. [Google Scholar] [CrossRef]
- Chen, S.S.; Shi, J.P.; Wei, J.J. A note on Hopf bifurcations in a delayed diffusive Lotka-Volterra predator-prey system. Comput. Math. Appl. 2011, 62, 2240–2245. [Google Scholar] [CrossRef]
- Zhao, M.; Zhang, L. Permanence and chaos in a host-parasitoid model with prolonged diapause for the host. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 4197–4203. [Google Scholar] [CrossRef]
- Yu, H.; Zhao, M. Seasonally perturbed prey-predator ecological system with the Beddington-DeAnglis functional response. Discrete Dyn. Nat. Soc. 2012, 2012, 150359. [Google Scholar] [CrossRef]
- Liu, Z.J.; Zhong, S.M. Permanence and extinction analysis for a delayed periodic predator-prey system with Holling type II response function and diffusion. Appl. Math. Comput. 2010, 216, 3002–3015. [Google Scholar] [CrossRef]
- Huo, H.F.; Li, W.T. Periodic solutions of delayed Leslie-Gower predator-prey models. Appl. Math. Comput. 2004, 155, 591–605. [Google Scholar] [CrossRef]
- Yuan, S.L.; Song, Y.L. Bifurcation and stability analysis for a delayed Leslie-Gower predator-prey system. IMA J. Appl. Math. 2009, 74, 574–603. [Google Scholar] [CrossRef]
- Leslie, P.H. Some further notes on the use of matrices in population mathematics. Biometrika 1948, 35, 213–245. [Google Scholar] [CrossRef]
- Leslie, P.H.; Gower, J.C. The properties of a stochastic model for the predator–prey type of interaction between two species. Biometrika 1960, 47, 219–234. [Google Scholar] [CrossRef]
- Aziz-Alaoui, M.A.; Okiye, M.D. Boundedness and global stability for a predator-prey model with modified Leslie-Gower and Holling type II schemes. Appl. Math. Lett. 2003, 16, 1069–1075. [Google Scholar] [CrossRef]
- Kox, M.; Sayler, G.S.; Schultz, T.W. Complex dynamics in a model microbial system. Bull. Math. Biol. 1992, 54, 619–648. [Google Scholar]
- Apreutesei, N.; Dimitriu, G. On a prey-predator reaction-diffusion system with a Holling type III functional response. J. Comput. Appl. Math. 2010, 235, 366–379. [Google Scholar] [CrossRef]
- Liu, Z.; Zhong, S.; Liu, X. Permanence and periodic solutions for an impulsive reaction-diffusion food-chain system with Holling type III functional response. J. Franklin Inst. 2011, 348, 277–299. [Google Scholar] [CrossRef]
- Schenk, D.; Bacher, S. Functional response of a generalist insect predator to one of its prey species in the field. J. Anim. Ecol. 2002, 71, 524–531. [Google Scholar] [CrossRef]
- Sugie, J.; Miyamoto, K.; Morino, K. Absence of limit cycles of a predator-prey system a sigmoid functional response. Appl. Math. Lett. 1996, 9, 85–90. [Google Scholar] [CrossRef]
- Lamontagne, Y.; Coutu, C.; Rousseau, C. Bifurcation analysis of a predator–prey system with generalized Holling type III functional response. J. Dyn. Diff. Equ. 2008, 20, 535–571. [Google Scholar] [CrossRef]
- Hochberg, M.E.; Hold, R.D. Refuge evolution and the population dynamics of coupled host-parasitoid association. Evol. Ecol. 1995, 9, 633–661. [Google Scholar] [CrossRef]
- Ma, Z.H.; Li, W.L.; Zhao, Y.; Wang, W.L.; Zhang, H.; Li, Z.Z. Effects of prey refuges on a predator-prey model with a class of functional responses: The role of refuges. Math. Biosci. 2009, 218, 73–79. [Google Scholar] [CrossRef] [PubMed]
- Guan, X.N.; Wang, W.M.; Cai, Y.L. Spatiotemporal dynamics of a Leslie-Gower predator-prey model incorporating a prey refuge. Nonlinear Anal. Real World Appl. 2011, 12, 2385–2395. [Google Scholar] [CrossRef]
- Huang, Y.J.; Chen, F.D.; Zhong, L. Stability analysis of a prey-predator model with Holling type III response function incorporating a prey refuge. Appl. Math. Comput. 2006, 182, 672–683. [Google Scholar] [CrossRef]
- Gonzalez-Olivares, E.; Ramos-Jiliberto, R. Dynamic of prey refuges in a simple model system: More prey, fewer predators and enhanced stability. Ecol. Modell. 2003, 166, 135–146. [Google Scholar] [CrossRef]
- Jia, Y.F.; Xu, H.K.; Agarwal, R.P. Existence of positive solutions for a prey-predator model with refuge and diffusion. Appl. Math. Comput. 2011, 217, 8264–8276. [Google Scholar]
- Camara, B.I. Waves analysis and spatiotemporal pattern formation of an ecosystem model. Nonlinear Anal. Real World Appl. 2011, 12, 2511–2528. [Google Scholar] [CrossRef]
- Turing, A.M. The chemical basis of morphogenesis. Philos. Trans. R. Soc. Lond B: Biol. Sci. 1952, 237, 37–72. [Google Scholar] [CrossRef]
- Zhu, L.M.; Wang, A.L.; Liu, Y.J.; Wang, B. Stationary patterns of a predator-prey model with spatial effect. Appl. Math. Comput. 2010, 216, 3620–3626. [Google Scholar] [CrossRef]
- Aly, S.; Kima, I.; Sheen, D. Turing instability for a ratio-dependent predator-prey model with diffusion. Appl. Math. Comput. 2011, 217, 7265–7281. [Google Scholar] [CrossRef]
- Banerjee, M.; Petrovskii, S. Self-organised spatial patterns and chaos in a ratio-dependent predator-prey system. Theor. Ecol. 2011, 4, 37–53. [Google Scholar] [CrossRef]
- Tian, Y.L.; Weng, P.X. Stability analysis of diffusive predator-prey model with modified Leslie-Gower and Holling type III schemes. Appl. Math. Comput. 2011, 218, 3733–3745. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhao, J.; Zhao, M.; Yu, H. Effect of Prey Refuge on the Spatiotemporal Dynamics of a Modified Leslie-Gower Predator-Prey System with Holling Type III Schemes. Entropy 2013, 15, 2431-2447. https://doi.org/10.3390/e15062431
Zhao J, Zhao M, Yu H. Effect of Prey Refuge on the Spatiotemporal Dynamics of a Modified Leslie-Gower Predator-Prey System with Holling Type III Schemes. Entropy. 2013; 15(6):2431-2447. https://doi.org/10.3390/e15062431
Chicago/Turabian StyleZhao, Jianglin, Min Zhao, and Hengguo Yu. 2013. "Effect of Prey Refuge on the Spatiotemporal Dynamics of a Modified Leslie-Gower Predator-Prey System with Holling Type III Schemes" Entropy 15, no. 6: 2431-2447. https://doi.org/10.3390/e15062431



