1. Introduction
Mutual information has been receiving increased attention in the recent years, in the field of
machine learning and
statistical pattern recognition, more specifically in
dimensionality reduction, also known as
feature extraction. In this paper we focus on the problem of
classification, in which a dataset of (usually high-dimensional) vectors are categorised into several distinct classes and presented as training data, and the task is to classify new data points into their correct categories. For this to be done feasibly and efficiently, a dimensionality reduction procedure needs to be carried out as a pre-processing step, where the dataset is projected onto a lower-dimensional space, whose basis vectors are often known as
features. The search for these features is known as
feature extraction in the machine learning literature [
1], and sometimes also known as
dimensionality reduction in the context of data visualisation and representation [
2].
The features are found by declaring an objective value to maximise or minimise, and those features with the highest objective values are retained as “good” features. For example, given any feature (a unit vector in the input space, which can be viewed as a line), we can project the training data points onto it, and estimate the mutual information between these projected data points and the class label (our target variable), and use this as the objective value to determine the quality of the feature. Indeed, Torkkola’s method [
3] maximises Kapur’s
quadratic mutual information (QMI) [
4] through gradient-ascent-type iterations. Another example of an objective value of a feature is the variance of the data along the feature, whose maximisation has a closed-form, eigenvalue-based solution, known as
principal component analysis (PCA) [
5]. In this paper however we want to focus on information-theoretic objective values, whose benefits over variance-based (or distance-based) objective values, at least for artificial datasets and low-dimensional datasets, have been demonstrated [
3,
6,
7]. The main advantage of using information-theoretic measures is illustrated in
Figure 1.
Figure 1.
This artificial 2D data is categorised into two classes: pink pentagons and blue stars. We can see that the black line is a better line of projection for the data, in terms of class-discrimination, than the blue dashed line. The blue dashed line is the feature computed using Fisher’s linear discriminant analysis (LDA) [
5]; PCA produces a very similar feature in this case. The black line is computed using our eigenvalue-based mutual information method [
8].
Figure 1.
This artificial 2D data is categorised into two classes: pink pentagons and blue stars. We can see that the black line is a better line of projection for the data, in terms of class-discrimination, than the blue dashed line. The blue dashed line is the feature computed using Fisher’s linear discriminant analysis (LDA) [
5]; PCA produces a very similar feature in this case. The black line is computed using our eigenvalue-based mutual information method [
8].
There are many difficulties associated with measuring mutual information from data. First of all, we do not know the true distribution of the data in the input space, which itself needs to be estimated from the training data. Secondly, Shannon’s measure of mutual information [
9,
10], when applied to continuous data, requires either numerical integration, which is extremely computationally expensive, or discretisation, which may lead to inaccurate estimation and does not lend itself to efficient optimisation techniques. Several attempts have been made to circumvent some of these difficulties through the use of alternative measures of information [
3,
4,
6,
11] and the popular technique of kernel density estimation [
12]. While these have proven to be effective techniques for measuring mutual information between the data along a feature and the class label, they can (so far) only be maximised through
iterative optimisation. This has its own complications with regards to dimensionality reduction. More specifically, they have many free variables, and the algorithms are very computationally expensive, much more so than non-information-theoretic dimensionality reduction techniques like PCA. A technique was proposed [
8] that avoids iterative optimisation, and instead has a closed-form, eigenvalue-based solution, similar in methodology to PCA. In this paper we will look at some more detailed properties of the underlying measure used therein, and show some connections with Laplacian eigenmaps [
2,
13].
2. Measures of Mutual Information
For the application of information theory to dimensionality reduction for classification problems, we study the mutual information between a continuous random variable
Y and a discrete random variable
C. Refer to
Table 1 for notation. Shannon’s mutual information in this case is
We want to avoid numerical computation of integrals because of their high computational cost. A common way of doing this is to discretise the continuous random variable
Y.
Mutual information as defined in Equation (
1) is the Kullback–Leibler (KL) divergence between a joint distribution
and the product of the respective marginal distributions
, or equivalently the joint distribution under the assumption of independence. The KL divergence can be characterised by a set of postulates [
11]. Kapur [
4] argued that if the aim is to maximise the divergence, and not so much to calculate its value precisely, then the set of postulates can be relaxed [
3]. A family of measures for the divergence of two distributions were proposed, and one of them results in the following
quadratic mutual information (QMI).
This takes a particularly convenient form when the densities
and
are estimated using Gaussian kernel density estimation [
12]. More specifically, the integral in Equation (
2) can be evaluated analytically using the convolution property of Gaussian densities [
3,
8]. We refer the reader to [
3,
8] for algebraic details, and only present the key results here. Equation (
2) can be re-written as follows.
where we use the short-hand notation
With this, the maximisation of QMI can (theoretically) be solved by differentiating Equation (
3) with respect to
and using a gradient-ascent-type algorithm. Note that in contrast, if we approximate
as in Equation (
1) by discretising the continuous random variable
Y as mentioned, then we cannot differentiate it with respect to
analytically. However there are methods that approximate the gradient of Shannon’s mutual information even when discretisation is used, and gradient ascent can be done with Shannon’s mutual information [
14].
Table 1.
Notation.
| Unit vector representing a feature. |
| Random vector variable representing a data point in the input space. |
| The training data point. |
| Y | Random variable representing a data point projected onto a feature . More precisely, . |
| , the training data point projected onto the feature . |
| C | A discrete random variable representing the class label of a data point. |
| The correct class label of the training data point. |
| Realisations of , Y, and C. |
| K | Total number of classes in the dataset. |
| N | Total number of training data points. |
| Size of training data class c. |
| Probability density function of Y at realisation y. Likewise for other variables. |
| σ | (bandwidth of the Gaussian kernel density estimator). |
Torkkola uses QMI as a measure of quality of features in his iterative feature extraction algorithm [
3]. It was shown that this technique can give superior classification results for some low-dimensional datasets, while the conventional feature extraction methods PCA and LDA perform better on others. No high-dimensional datasets were tested on however, possibly due to the high computational complexity of iterative algorithms. QMI is a theoretically elegant and practically applicable measure of mutual information. Regarding its optimisation however, there are practical drawbacks, which can be summarised as follows.
Table 2.
Times taken, in seconds, for algorithms PCA, LDA, eigenvalue-based MI, and iterative QMI to extract one feature and 39 features respectively, from the AT&T Dataset of Faces. The computing times for eigenvalue-based algorithms (PCA, LDA, EMI) are independent of the number of extracted features, due to the closed-form nature of the eigenvalue problem. This was a Python 2.7 implementation with packages Numpy, MatPltoLib, and PIL (Python Imaging Library), executed on an Intel Core i7-2600K processor at 3.40 GHz with 16 GB RAM.
Table 2.
Times taken, in seconds, for algorithms PCA, LDA, eigenvalue-based MI, and iterative QMI to extract one feature and 39 features respectively, from the AT&T Dataset of Faces. The computing times for eigenvalue-based algorithms (PCA, LDA, EMI) are independent of the number of extracted features, due to the closed-form nature of the eigenvalue problem. This was a Python 2.7 implementation with packages Numpy, MatPltoLib, and PIL (Python Imaging Library), executed on an Intel Core i7-2600K processor at 3.40 GHz with 16 GB RAM.
| | Time to extract |
|---|
| | first feature | 39 features |
|---|
| PCA | 0.406 | (0.406) |
| LDA | 1.185 | (1.185) |
| EMI | 4.992 | (4.992) |
| QMI | 265.034 | 10330.358 |
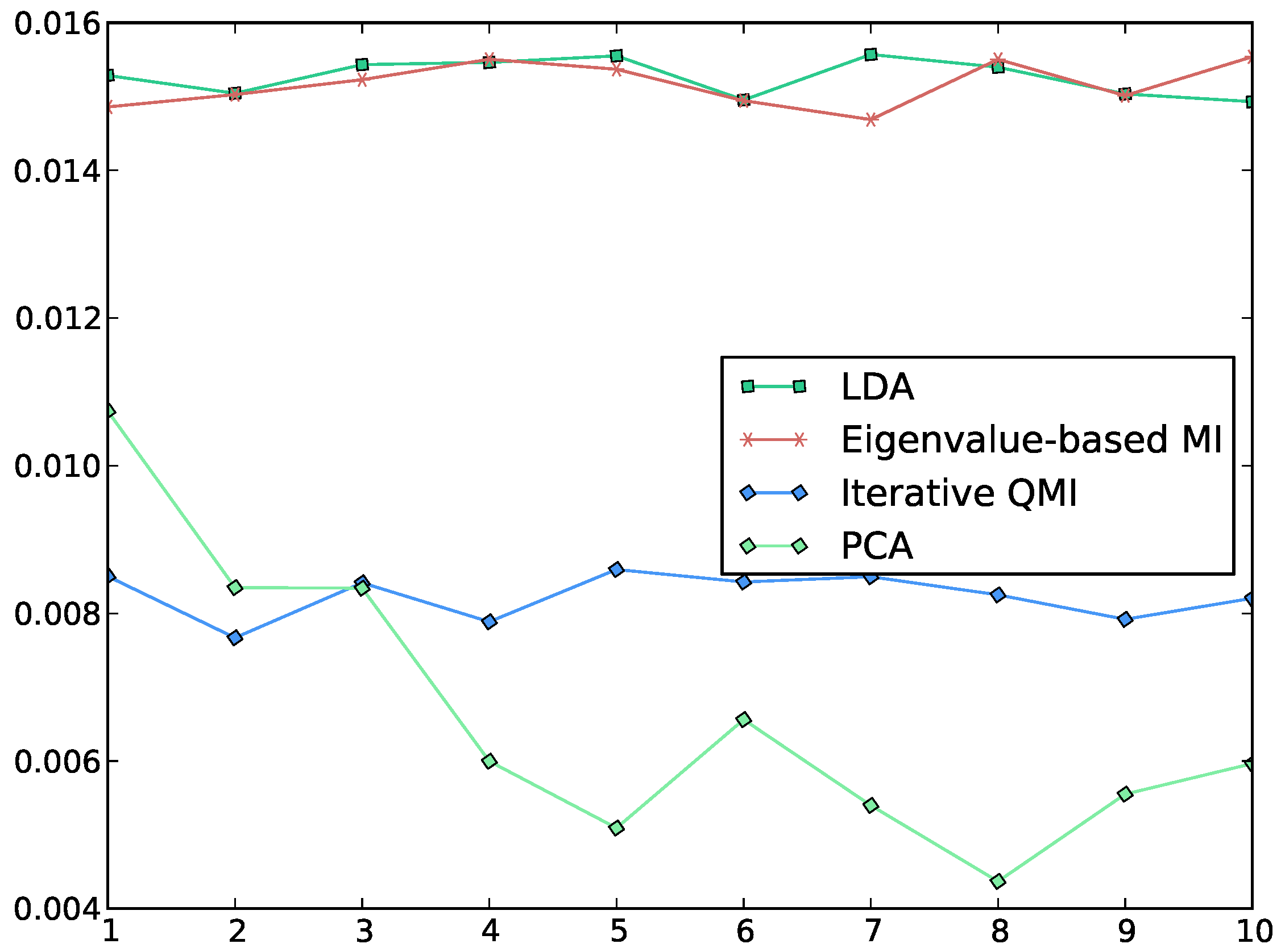
In
Figure 2, the reader may ask why LDA produces high values of QMI, similar to that produced by the EMI method, despite that LDA is not designed to maximise QMI. To answer this question, first note that Equation (
2) can be re-written as
Let us consider a simple 2-class example, where both classes have equal prior probabilities
. In this case, Equation (
6) tells us that
is proportional to a sum of two summands, each of which is the square of the area between the graphs of the class-conditional distribution
and the overall distribution
. Let us suppose further that the classes are normally distributed with the same variance but different means. Then
Figure 3 shows us that maximising QMI is equivalent to minimising the overlap between the 2 class-conditional distributions, or equivalently maximising the separation between the classes.
Figure 2.
Plot of the QMI between the class label and each of the first 10 features, computed by various methods. The horizontal axis indexes the features, while the vertical axis measures the QMI along each feature. We see that Torkkola’s iterative QMI algorithm [
3] gives lower values of QMI than the EMI algorithm, which gives values similar to LDA. Note that LDA is not designed to maximise QMI. PCA is also included for the sake of comparison. In the experiment, the data was whitened and the initial features for the iterative QMI algorithm were set to random features.
Figure 2.
Plot of the QMI between the class label and each of the first 10 features, computed by various methods. The horizontal axis indexes the features, while the vertical axis measures the QMI along each feature. We see that Torkkola’s iterative QMI algorithm [
3] gives lower values of QMI than the EMI algorithm, which gives values similar to LDA. Note that LDA is not designed to maximise QMI. PCA is also included for the sake of comparison. In the experiment, the data was whitened and the initial features for the iterative QMI algorithm were set to random features.
Figure 3.
The solid lines are the class-conditional distributions for the 2 classes, and the dotted line is the overall distribution . The checkered and the dotted areas correspond to the value of for each of the 2 classes respectively, and the squares of only these areas contribute to the value of QMI, not the grey-shaded area. The grey-shaded area is the overlap between the two class-conditional distributions. We see that the smaller the overlap, the larger the value of the dotted and checkered areas, and therefore the larger the value of QMI. (a) Good class separation, high QMI; (b) Bad class separation, lower QMI.
Figure 3.
The solid lines are the class-conditional distributions for the 2 classes, and the dotted line is the overall distribution . The checkered and the dotted areas correspond to the value of for each of the 2 classes respectively, and the squares of only these areas contribute to the value of QMI, not the grey-shaded area. The grey-shaded area is the overlap between the two class-conditional distributions. We see that the smaller the overlap, the larger the value of the dotted and checkered areas, and therefore the larger the value of QMI. (a) Good class separation, high QMI; (b) Bad class separation, lower QMI.
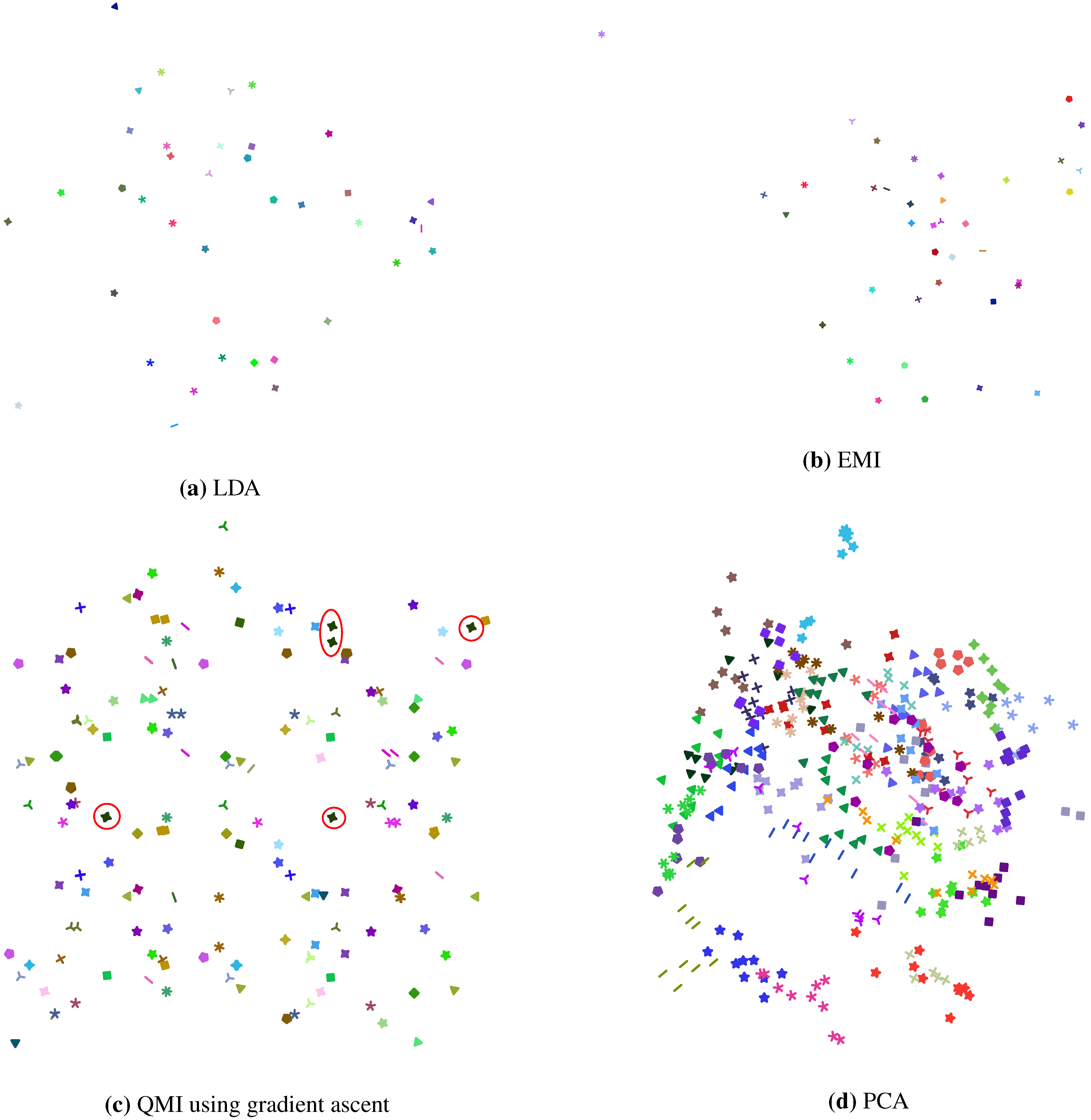
Figure 4.
2D projections of the AT&T Dataset of Faces, computed using (a) LDA; (b) our EMI method; (c) Torkkola’s iterative QMI method; and (d) PCA for comparison. In (a) we see that each of the 40 classes in the dataset is in a compact cluster, well separated from others. In fact, each class is so tightly packed that at this resolution it looks like a singleton point. Similar observations can be made from (b). In (c) however, each class seems to be scattered into 2 or more clusters, as exemplified by the class marked by red circles. Note that each class of the dataset has 10 data points, and the class marked by red circles seems to be in 4 clusters. For all of (a), (b) and (c), the data was whitened as a pre-processing step.
Figure 4.
2D projections of the AT&T Dataset of Faces, computed using (a) LDA; (b) our EMI method; (c) Torkkola’s iterative QMI method; and (d) PCA for comparison. In (a) we see that each of the 40 classes in the dataset is in a compact cluster, well separated from others. In fact, each class is so tightly packed that at this resolution it looks like a singleton point. Similar observations can be made from (b). In (c) however, each class seems to be scattered into 2 or more clusters, as exemplified by the class marked by red circles. Note that each class of the dataset has 10 data points, and the class marked by red circles seems to be in 4 clusters. For all of (a), (b) and (c), the data was whitened as a pre-processing step.
The intuition shown in
Figure 3 can be validly extrapolated to higher dimensions, general class-conditional distributions, and multi-class datasets. LDA maximises the class-separation of the data in the sense that it maximises the between-class distances and minimises within-class distances between data points. Now depending on the class-conditional distributions and input dimensionality, LDA will not always succeed, as illustrated in
Figure 1. However, where LDA does succeed, different classes will be well-separated and so the QMI along the features produced by LDA will be high. The AT&T Dataset of Faces is one in which LDA does succeed in maximising the separation between classes, as shown in
Figure 4a. In fact, as a side-note, our experiments show that LDA succeeds in many high-dimensional face datasets. The reasons for this have little to do with mutual information but rather a lot to do with the high input dimensionality and the problem of over-fitting, and therefore are not within the scope of this paper. The similarity in the values of QMI obtained by LDA and our EMI method is explained by the similarity in their respective 2D projections shown in
Figure 4a and
Figure 4b.
Figure 4c, in contrast, does not exhibit good separation between classes, which explains the relatively low values of QMI obtained by the iterative method as shown in
Figure 2. Furthermore,
Figure 4c suggests that the iterative QMI method in this case might have sought a local optimum, due to the scattering nature of individual classes into more than one cluster.
2.1. Eigenvalue-Based Mutual Information (EMI)
The practical drawbacks of QMI with respect to its maximisation, as mentioned previously, can be circumvented through the use of another measure of mutual information. This measure was implicitly employed in [
8] to address the practical problems with QMI. The maximisation of this measure of mutual information, which for now we will call EMI (eigenvalue-based mutual information), has a closed-form solution that is a set of eigenvectors of an objective matrix. Before we introduce EMI, we will briefly review the
pairwise interaction interpretation of QMI.
Mutual information is often interpreted as the
difference or
similarity between two probability distributions: the true joint distribution and the joint distribution under the independence assumption. In the context of estimating mutual information
from data however, Equation (
3) uncovers an alternative view of mutual information, one in terms of
pairwise interactions between each pair
of training data points, weighted by the
. This view is especially applicable and intuitive in classification problems. Each pairwise interaction
is monotonically decreasing in the distance
between two data points along the feature
, as is clear from Equation (
5). So for example if we simply wanted to maximise the sum
(rather than Equation (
3)), then we will obtain a feature along which the data points are as close to each other as possible, which is obviously not desirable from a classification perspective. However the weights
can be negative, in which case the corresponding pairwise distance is maximised. Let us conceive of a simple example in which there are 2 classes (
), and each class has 5 training data points (
and
). Then the reader may verify from Equation (
4) that if two data points
and
are in the same class, then
; and if they are in different classes, then
. This means that in the maximisation of
as in Equation (
3), the within-class distances are minimised while the between-class distances are maximised. On a side-note, we see that in this pairwise interaction view of mutual information maximisation, there is significant resemblance to LDA. However, unlike LDA, QMI has advantageous information-theoretic properties as illustrated by
Figure 1.
Another consequence of this view of mutual information is that we can now generalise the pairwise interactions between data points. In QMI with Gaussian kernel density estimation, each pairwise interaction is a Gaussian function of . The salient characteristics of that give its information-theoretic properties are as follows. Note that since by definition and that , we always have .
It is symmetric in and monotonically decreasing in .
It reaches its maximum when , where the maximum is .
It reaches its minimum when , where the minimum is .
All of these properties can be preserved by using an alternative,
negative-parabolic (as opposed to Gaussian) pairwise interaction, in the form of
. More precisely, define
We see that if we view
as the abscissa, then the graph of
in Equation (
7) is a negative parabola, hence the name
negative parabolic pairwise interaction.
Figure 5 illustrates the differences and similarities between
and
.
Figure 5.
Graphs of
as in Equation (
7), and
as in Equation (
5), where we view
as the abscissa. The two pairwise interactions agree at their maximum (in the middle) and at their minima (two sides).
Figure 5.
Graphs of
as in Equation (
7), and
as in Equation (
5), where we view
as the abscissa. The two pairwise interactions agree at their maximum (in the middle) and at their minima (two sides).
Now we can measure the mutual information between the data and the class label by using the following, instead of QMI as in Equation (
2).
where
is the same as in Equation (
4). For the example dataset in
Figure 1, the black line is the feature along which the maximum value of
is obtained. We call
eigenvalue-based mutual information (EMI), for reasons that will become clear shortly.
Figure 6 demonstrates the similarities between EMI, QMI and Shannon’s MI (Equation (
1)).
The real advantage of using EMI instead of QMI is that it can be optimised analytically, obviating the need for any iterative procedure.
can be written as
where
where the second line follows from evaluating the matrix exponential in the first line. Thus, if we define a matrix
E by
then we see that EMI can be written as
IE(
Y;
C) =
wTEw. Now finding a feature that maximises EMI is equivalent to maximising
IE(
Y;
C) in
w, and we see that the maximising
w are just the largest eigenvectors of the matrix
E.
The reader may notice some similarities between
enm and the
Epanechnikov kernel, which is defined as follows.
This also has a negative parabolic shape, but there are several fundamental differences between this and our pairwise interaction
enm. First,
enm has a variable width that depends on
, while in contrast
hnm does not, and is fixed-width. In particular,
hnm does not take into account any pairs of points for which
. Moreover, the indicator function
cannot be encoded in a matrix in the way that
enm can be encoded in the matrix
Enm (Equation (9)) via
enm =
wTEnmw. It is the ability of a pairwise interaction (or kernel) to be encoded in a matrix that allows the associated dimensionality reduction algorithm to be formulated as an eigenvalue-problem.
We end this section with a brief illustration of a practical application of EMI. More experiments using EMI can be found in [
8].
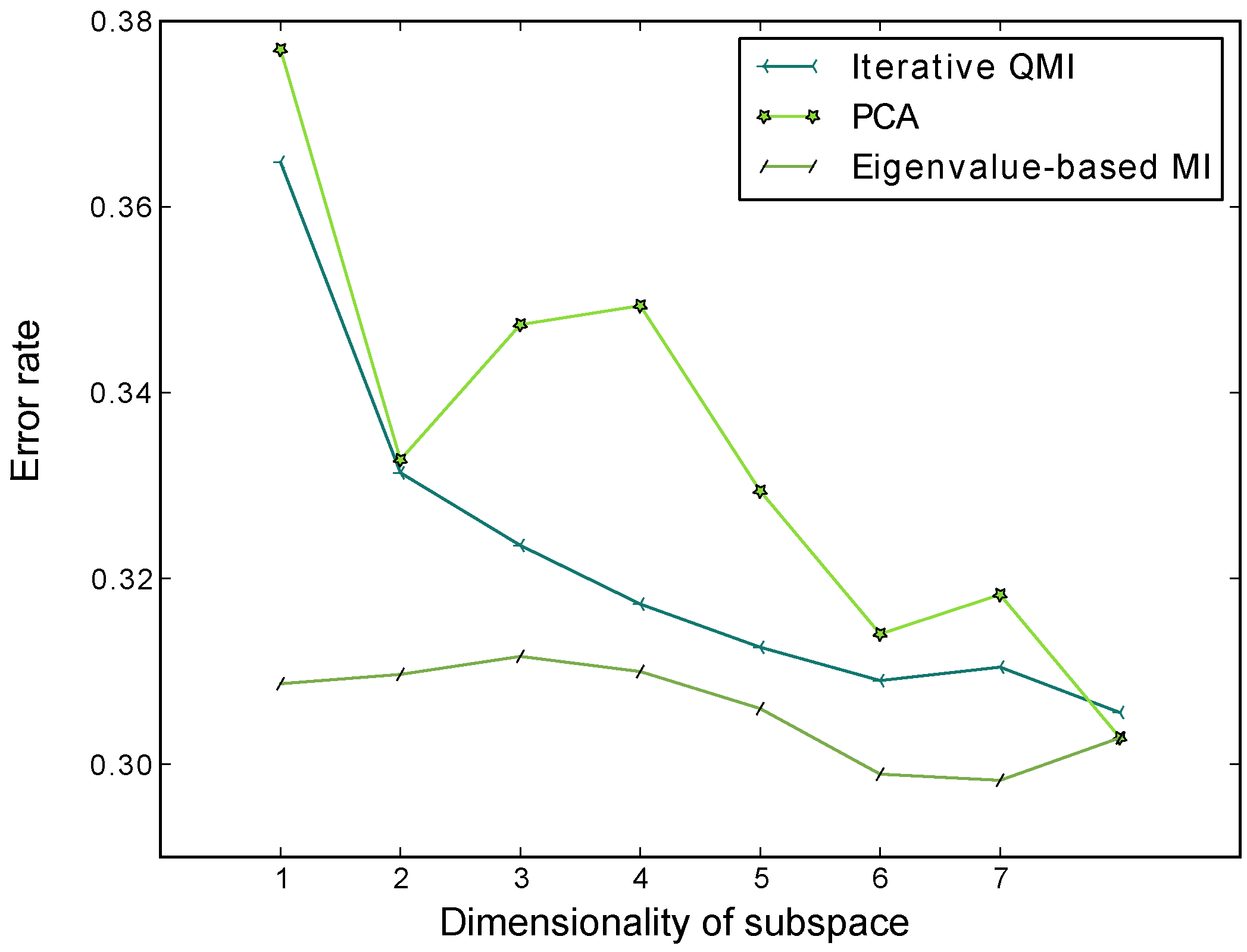
Figure 7 shows the average classification error rates of the nearest-neighbour classifier through 10 repeats of 5-fold cross-validation, for the subspaces computed by PCA, the EMI method, and the iterative QMI method respectively, using the Pima Indians Diabetes Dataset available from the UCI machine learning repository.
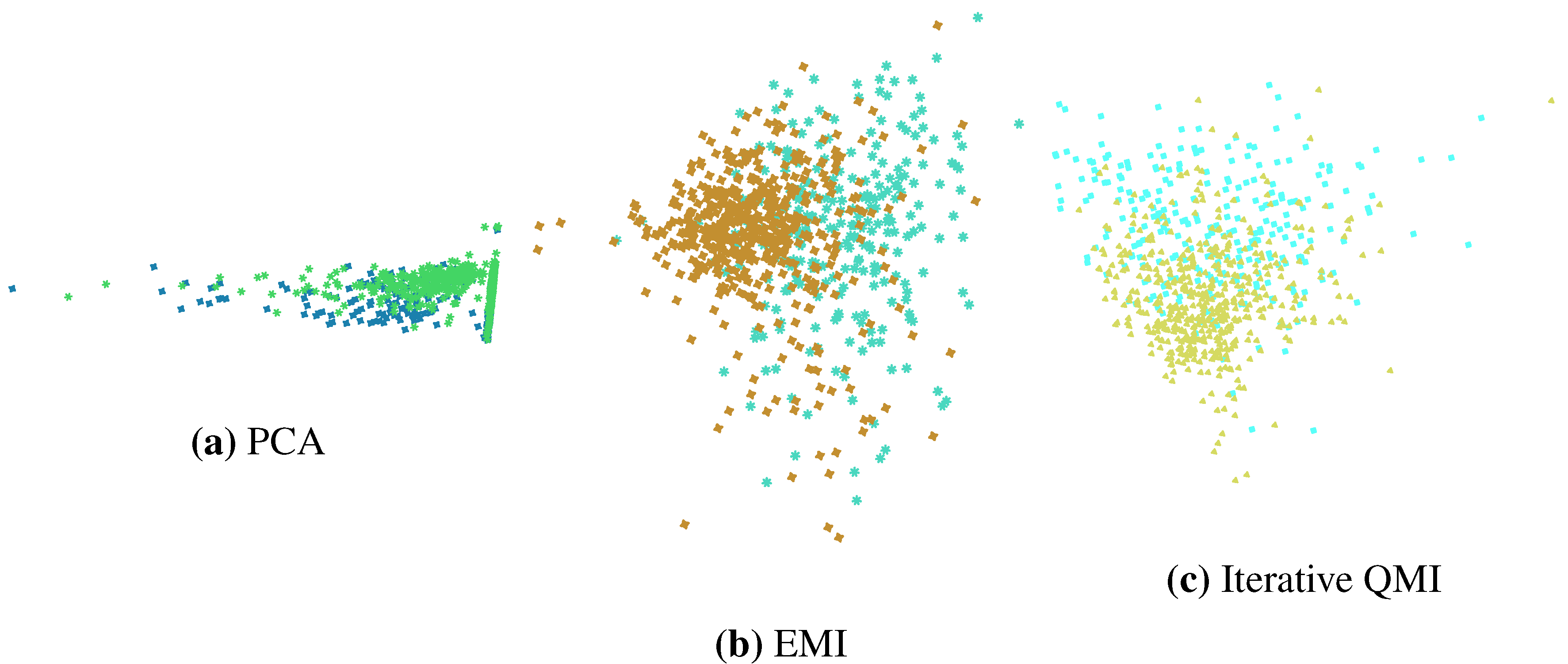
Figure 8 shows the 2D projections computed by the three methods. Note the similarity between the projections computed by the two information-theoretic methods, in contrast to that of PCA. Note also that a 2D projection cannot be computed using LDA since this is a 2-class problem and LDA would only be able to compute one feature.
Figure 6.
The values of the various measures of mutual information along a feature, as the feature is rotated
π radians. The dataset used is the one shown in
Figure 1. Note that some of the measures are rescaled so that all measures are visually comparable. However, it is not the actual value of the measure that matters in the context of optimisation, but rather the shape of the graph. We see that EMI, QMI and traditional MI peak at almost the same place. For the sake of comparison, a non-information theoretic measure is included, that is, Fisher’s discriminant (LDA). We see that Fisher’s discriminant measure does not peak at the “right” place. The Fisher-optimal feature (computed by LDA) is shown as the blue dashed line in
Figure 1.
Figure 6.
The values of the various measures of mutual information along a feature, as the feature is rotated
π radians. The dataset used is the one shown in
Figure 1. Note that some of the measures are rescaled so that all measures are visually comparable. However, it is not the actual value of the measure that matters in the context of optimisation, but rather the shape of the graph. We see that EMI, QMI and traditional MI peak at almost the same place. For the sake of comparison, a non-information theoretic measure is included, that is, Fisher’s discriminant (LDA). We see that Fisher’s discriminant measure does not peak at the “right” place. The Fisher-optimal feature (computed by LDA) is shown as the blue dashed line in
Figure 1.
Figure 7.
Average classification error rates of the nearest-neighbour classifier through 10 repeats of 5-fold cross-validation, for the subspaces computed by PCA, EMI and the iterative QMI method respectively. The dataset used is the Pima Indians Diabetes Dataset, available from the UCI Machine Learning Repository. LDA was not included in this evaluation because the dataset only has 2 classes and LDA would only be able to extract one feature. We see that EMI has lower error rates than PCA and Torkkola’s iterative QMI method.
Figure 7.
Average classification error rates of the nearest-neighbour classifier through 10 repeats of 5-fold cross-validation, for the subspaces computed by PCA, EMI and the iterative QMI method respectively. The dataset used is the Pima Indians Diabetes Dataset, available from the UCI Machine Learning Repository. LDA was not included in this evaluation because the dataset only has 2 classes and LDA would only be able to extract one feature. We see that EMI has lower error rates than PCA and Torkkola’s iterative QMI method.
Figure 8.
2D projections of the Pima dataset computed by three feature extraction techniques.
Figure 8.
2D projections of the Pima dataset computed by three feature extraction techniques.
3. Relationship between EMI and Laplacian Eigenmaps
Laplacian eigenmaps [
2,
13] is a dimensionality reduction technique that is based on preserving local properties of the data. While information-theoretic techniques aim to find low-dimensional subspaces that maximise the mutual information between the data and the class label, Laplacian eigenmaps find low-dimensional subspaces that minimize the distances between nearby data points. This is achieved by using pairwise weights
on pairs of data points
. The general problem is to maximise (or minimise) (see
Table 3 for notation)
As an aside, this can be viewed as a generalisation to PCA, since the problem of PCA can be viewed as the maximisation of a special case of (
12) where all the weights
are 1. The solution to the general problem (
12) are the (largest or smallest) eigenvectors of the matrix
.
L is called a
Laplacian matrix, it is symmetric and has the property that each row (column) sums to 0. We refer the reader to [
13] for more algebraic details regarding Laplacian eigenmaps.
Table 3.
Extra notation.
| Design matrix, whose row is the data point |
| The data point projected onto a low-dimensional subspace. If the dimensionality of the subspace is 1, then we use the notation (Table 1). |
| The design matrix in a low-dimensional subspace, whose row is the projected data point |
| A vector, all of whose elements are 1. |
| Pairwise weights used in Laplacian eigenmaps. |
| Ω | The weight matrix, whose element is . |
| L | The Laplacian matrix, defined by . |
From Equations (
7) and (
8), we can re-write the EMI along a feature
as the following.
Note that the first term on the right-hand-side of Equation (
13) does not involve
, and so is irrelevant in the maximisation. If we want a low-dimensional subspace spanned by
M features
that maximises the EMI along each feature, then the quantity we aim to maximise can be written as follows.
Now if we define the pairwise weights
noting that the first term on the right-hand-side of Equation (
14) does not involve
, we see that maximising EMI as in Equation (
14) is equivalent to minimising expression (
12), whose solution is given by the smallest eigenvectors of the matrix
.
In
Section 2.1 we saw that we can view EMI as an alternative to QMI where we use negative parabolic pairwise interactions instead of Gaussian pairwise interactions between training data points. In this section we see that another view of EMI maximisation is a special case of Laplacian eigenmaps, where the weights are chosen as in Equation (
15). While the Laplacian eigenmaps method has been shown to bear some relation to maximum entropy methods in unsupervised dimensionality reduction [
15], so far it has not been shown to be related to mutual information. Hence, it is interesting to see that a set of weights
can be discovered (Equation (
15)) that produces a special case of Laplacian eigenmaps maximising an estimate of mutual information.
The difference between EMI maximisation and the original formulation of Laplacian eigenmaps is that in the original formulation of Laplacian eigenmaps, the weight matrix Ω, and consequently the Laplacian matrix L, is sparse. In contrast, the weight matrix and the Laplacian matrix for EMI maximisation are dense.
4. Conclusions and Further Research
We have introduced a measure of mutual information between a dataset and a discrete target variable (class label) that can be maximised analytically and has practical advantages over the current state-of-the-art QMI. The motivation for using information-theoretic measures in dimensionality reduction stems from the fact that classic non-information-theoretic techniques, such as PCA and LDA, deteriorate for some data distributions, as shown in
Figure 1. We have studied the pairwise interaction view of QMI, which led to the formulation of EMI. We have shown some similarities and differences between EMI and other measures of mutual information, and have briefly demonstrated the practical applicability of EMI in dimensionality reduction for classification. Finally, we have shown some relationships between EMI and Laplacian eigenmaps, which is a widely used dimensionality reduction algorithm.
The behaviour of information-theoretic algorithms for dimensionality reduction can be counterintuitive in high-dimensional spaces. The dataset used in our experiment in
Figure 7 is relatively low-dimensional. High dimensional datasets pose a computational challenge for information-theoretic algorithms, due to the high computational complexity of iterative algorithms for QMI maximisation. With the introduction of EMI, it is now possible study the behaviour of information-theoretic dimensionality reduction for high-dimensional datasets, such as face and image recognition, at a significantly lower computational cost. However, for high-dimensional data, our experiments have shown that while EMI maximisation is good for data visualisation and representation, it gives poor classification results. Our current experiments indicate that this is due to
over-fitting [
5,
16]. A recent review of dimensionality reduction algorithms [
2] has found that despite the sophistication of more modern algorithms, the best classification performance for real-world data is typically observed with PCA. Our current experimental results agree with this. It seems that the reason for this lies in the fact that the benefits offered by MI-based methods over traditional methods (
Figure 1) become less relevant in high-dimensional spaces, where classic non-information-theoretic methods such as LDA often succeed in maximising class-discrimination. We briefly discussed this in
Section 2 (
Figure 4). Future research into the exact mechanisms that generate this phenomenon and whether we can
reliably improve on PCA for real-world data (as opposed to for only a small subset of applications) will be of great practical importance.