2.1. RMSD and Residue MSF
Four independent 60 ns runs are utilized for sampling the conformational space of the apo and DHAP-bound enzyme more effectively. The root mean square deviations (RMSD) of the snapshots with respect to the initial (energetically minimized) structure are plotted in
Figure S1 for each trajectory. The RMSD calculation is carried out based on C
α atoms after alignment of each snapshot onto the initial structure. RMSD profiles fall within reasonable limits (2–3 Å), implying the reliability of each trajectory. Based on these profiles, first 10 ns of each simulation is discarded as equilibration period and the remaining 10–60 ns range is considered in the analysis of time-averaged properties. In Complex1 simulation, both DHAP molecules stay bound to the catalytic sites located in each subunit. In Complex2, DHAP in monomer A detaches from the catalytic site at around 13
th ns (just after equilibration period), whereas DHAP in the catalytic site of monomer B stays bound throughout the same run. For this reason, averaged properties for the complex are obtained using Complex1 A and B and Complex2 B subunits. In the case of apo simulations, A and B subunits from both runs are considered in the averages.
Mean square fluctuations (MSF) of alpha-carbon atoms of each residue are calculated based on the average structure of each trajectory. Average profiles for the apo and complex are plotted in
Figure 1. The overall mobility of the enzyme is constrained in the presence of the DHAP. Interestingly, this effect is not apparent in residues that are in close contact with DHAP (see inset in
Figure 1). In contrast, mobility of relatively distant residues that include the interface between subunits and some outlying helices (shown in blue in the inset) are effectively reduced. Specifically, only three residues (shown in red) that are located on loop 6 exhibit higher MSF in the complex: P166 at the N-terminus (23% increase in MSF), T175 and A176 at the C-terminus (~45%).
Figure 1.
Residue MSF for apo and complex simulations. Inset figure shows the complex residues with reduced (blue) and increased (red) MSF by 20% compared to apo. Green regions have similar MSF in both apo and complex simulations. DHAP is shown with stick representation.
Figure 1.
Residue MSF for apo and complex simulations. Inset figure shows the complex residues with reduced (blue) and increased (red) MSF by 20% compared to apo. Green regions have similar MSF in both apo and complex simulations. DHAP is shown with stick representation.
During the simulations, DHAP molecules make H-bonding with certain residues: N11, K13, H95, E165, G171, S211, G232 and G233. In this list, the first four are the catalytic residues. G171 is located at the tip of loop 6, S211 is on loop 7 and residues G232 and G233 are on loop 8. All of these residues have been reported as H-bonding contributor residues to the active site geometry [
1]. In the case of Complex2 monomer A, H-bonds between DHAP and residues N11, H95 are no longer observed after 9th ns as seen in
2b. This is followed by the breakage of H-bonds with E165, G233. Finally at 13 ns, H-bonding between DHAP and K13, S211 is broken, which leads to the detachment of the substrate from the active site. The number of H-bonds made between TIM residues and DHAP throughout each simulation is given in
Figure S2.
2.2. Loop 6 Opening/Closure is Observed in the Presence of DHAP
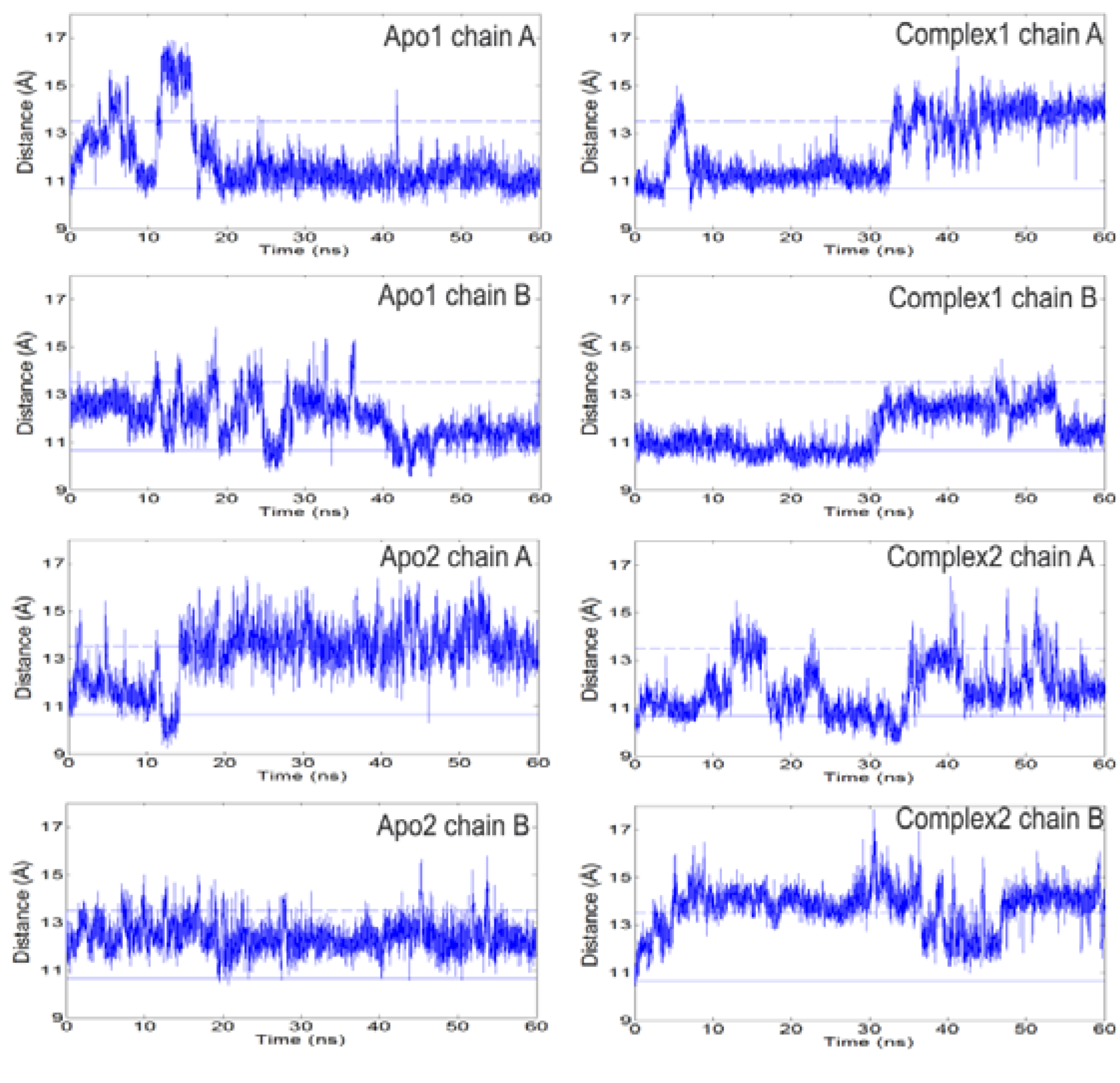
The open/closed states of loop 6 can be detected looking at the C
α-C
α distances between loop 6 tip residues (I170, G171, T172) and residue Y208 [
7,
9]. These distances are plotted as a function of time for both chains in each simulation as in
Figure 2,
Figures S3–4. There is no correlation between the A and B subunits for the specific distances reported. Solid (lower) and dashed (upper) horizontal lines in
Figure 2 refer to the I170-Y208 distances in the ligand-bound/closed (1TPH, smallest distance among the two chains) and apo/open (8TIM, largest distance) X-ray structures, respectively. In previous MD studies on apo TIM from chicken [
7,
9] and
Trypanosoma cruzi [
10], multiple opening/closure events of loop 6 have been observed during independent 60–100 ns runs.
Figure 2.
The distance between Cα atoms of loop 6 tip residue (I170) and a reference residue (Y208) as a function of time. Left and right panels summarize the profiles for apo and complex simulations. Solid and dashed lines indicate the respective closed and open states of the loop based on crystal structures. Loop 6 samples open conformations even in the presence of DHAP. It opens/closes multiple times during apo and complex simulations.
Figure 2.
The distance between Cα atoms of loop 6 tip residue (I170) and a reference residue (Y208) as a function of time. Left and right panels summarize the profiles for apo and complex simulations. Solid and dashed lines indicate the respective closed and open states of the loop based on crystal structures. Loop 6 samples open conformations even in the presence of DHAP. It opens/closes multiple times during apo and complex simulations.
It is known that for effective catalysis this loop should stay closed so that the active site is shielded from solvent [
1,
2]. In the presence of DHAP, the catalytic loop still opens and closes several times during our independent 60 ns runs. Concurrently, either one or both DHAP molecules stay bound at the active site. This interesting situation indicates that electrostatic interactions between substrate and loop 6 are not strong enough to keep the catalytic loop closed over the active site for extended periods. In fact, this could provide a means for effective product release (DHAP), which is not the rate-limiting step in the conversion of GAP to DHAP [
1,
14]. Also in conformity with our current findings, there are two crystal structures reported, in which the loop 6 is in open conformation despite the presence of a ligand [
1,
15,
16].
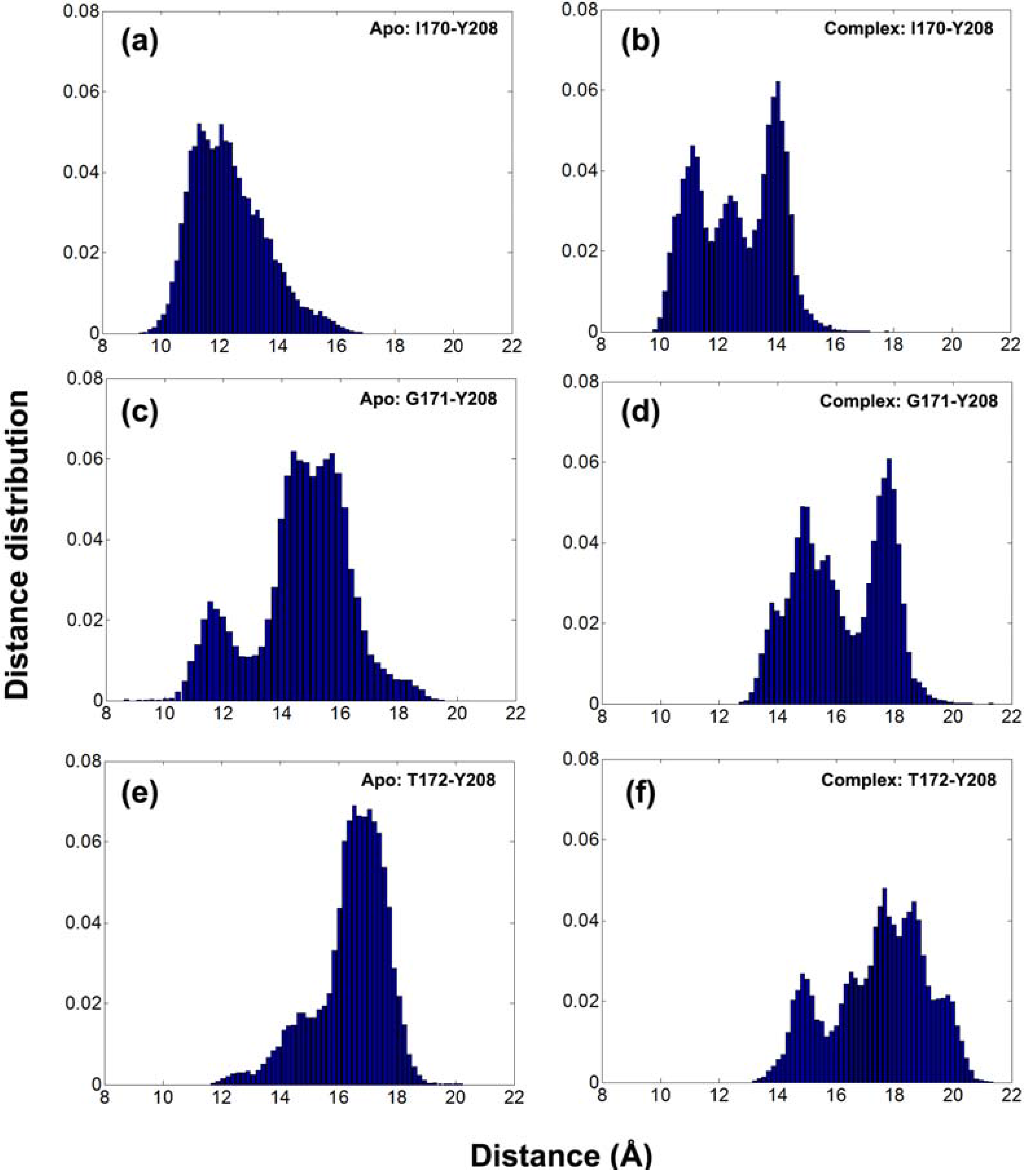
Furthermore, the distance histograms for the three tip residues on loop 6 are calculated using all recorded snapshots for apo (left panels) and DHAP-bound (right panels) subunits in
Figure 3. In fact, larger distances are sampled in the complex compared to apo simulations. Multiple peaks are observed around 11.5, 12.5 and 14 Å for I170-Y208, 15 and 17.5 Å for G171-Y208, 14.5, 17.5 and 18.5 Å for T172-Y208 distances in complex simulation, whereas the values for apo cases are around 12 Å for I170-Y208, 11.5 and 15 Å for G171-Y208 and 17 Å for T172-Y208 distances.
2.3. Essential Dynamics
In order to investigate the effects of DHAP on the enzyme dynamics, PCA is applied on each trajectory, as explained in Materials and Methods. Contribution of first five PCs to overall motion (percentage variance captured by PCs) is given in
Table S1.
Table 1 lists the overlap of loop 6 motion with the loop closure direction in the essential modes for both chains.
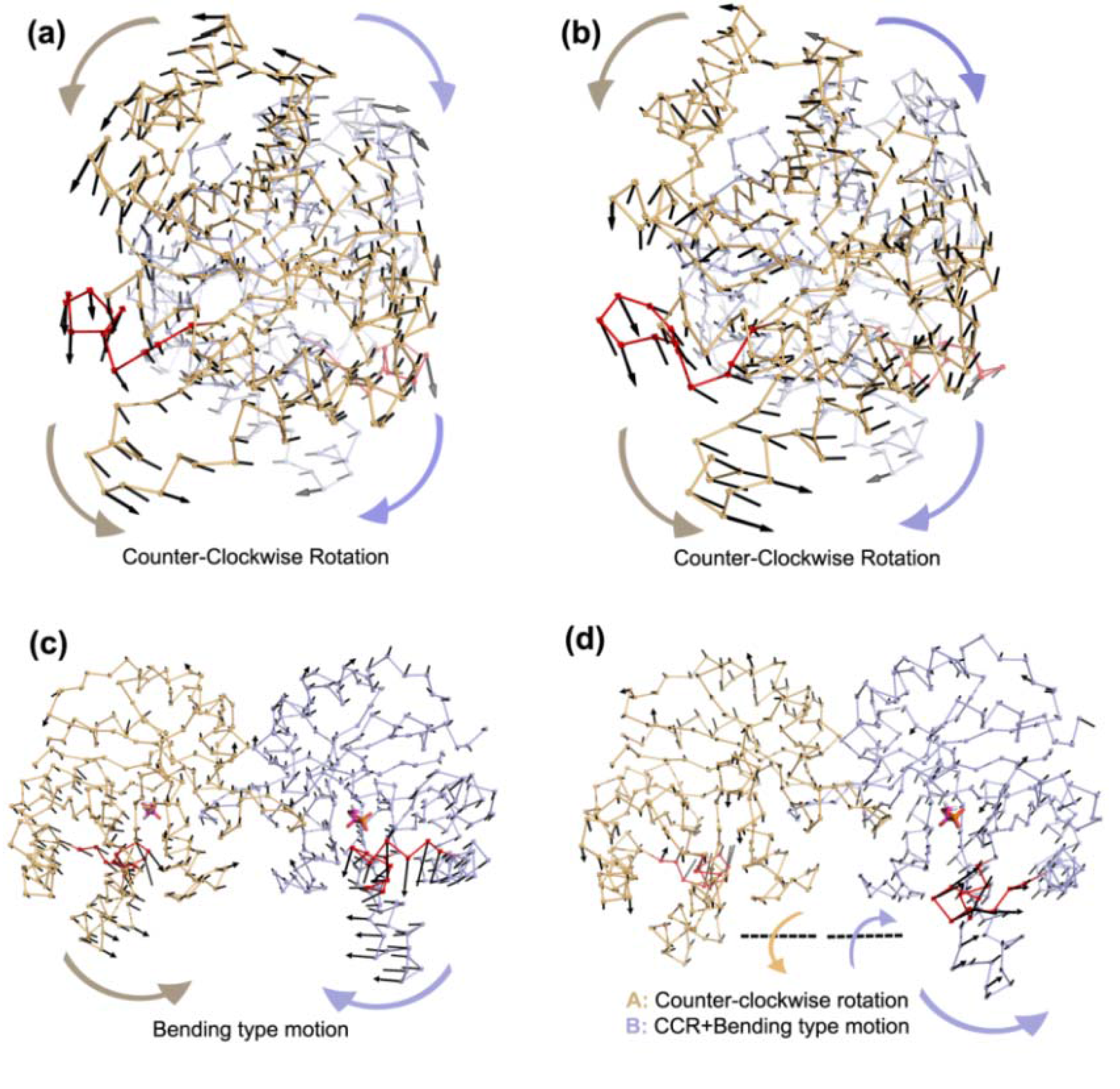
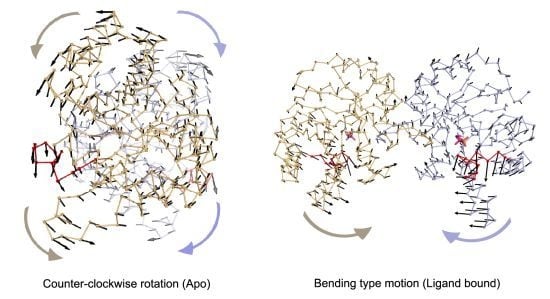
In apo simulations, PC1 corresponds to counter-clockwise rotation of subunits, which contributes 34% and 19% to overall motion in Apo1 and Apo2 simulations, respectively. In apo simulations, this motion is coupled with loop 6 opening/closing motion as seen in
Figure 4a,b and
Table 1 (more stressed in Apo1). In TIM-DHAP complexes, this counter-clockwise rotation does not appear in the essential modes for the subunits with DHAP. Still in some PCs, a similar type of rotation is detected as seen in the PC overlap figures (
Figure S5) and
Figure 4, but it lacks full coordination possibly due to the presence of DHAP molecules.
Table 1.
Loop 6 overlap with closure direction (overall PCA).
Table 1.
Loop 6 overlap with closure direction (overall PCA).
| PC | Apo1 | Apo2 | Complex1 | Complex2 |
| A | B | A | B | A | B | A | B |
| 1 | 0.76 | 0.59 | 0.37 | 0.44 | 0.58 | 0.68 | 0.75 | 0.18 |
| 2 | 0.42 | 0.04 | 0.24 | 0.14 | 0.76 | 0.61 | 0.74 | 0.10 |
| 3 | 0.14 | 0.08 | 0.06 | 0.58 | 0.17 | 0.75 | 0.22 | 0.00 |
| 4 | 0.78 | 0.81 | 0.49 | 0.26 | 0.28 | 0.49 | 0.81 | 0.54 |
| 5 | 0.41 | 0.16 | 0.24 | 0.48 | 0.55 | 0.11 | 0.25 | 0.54 |
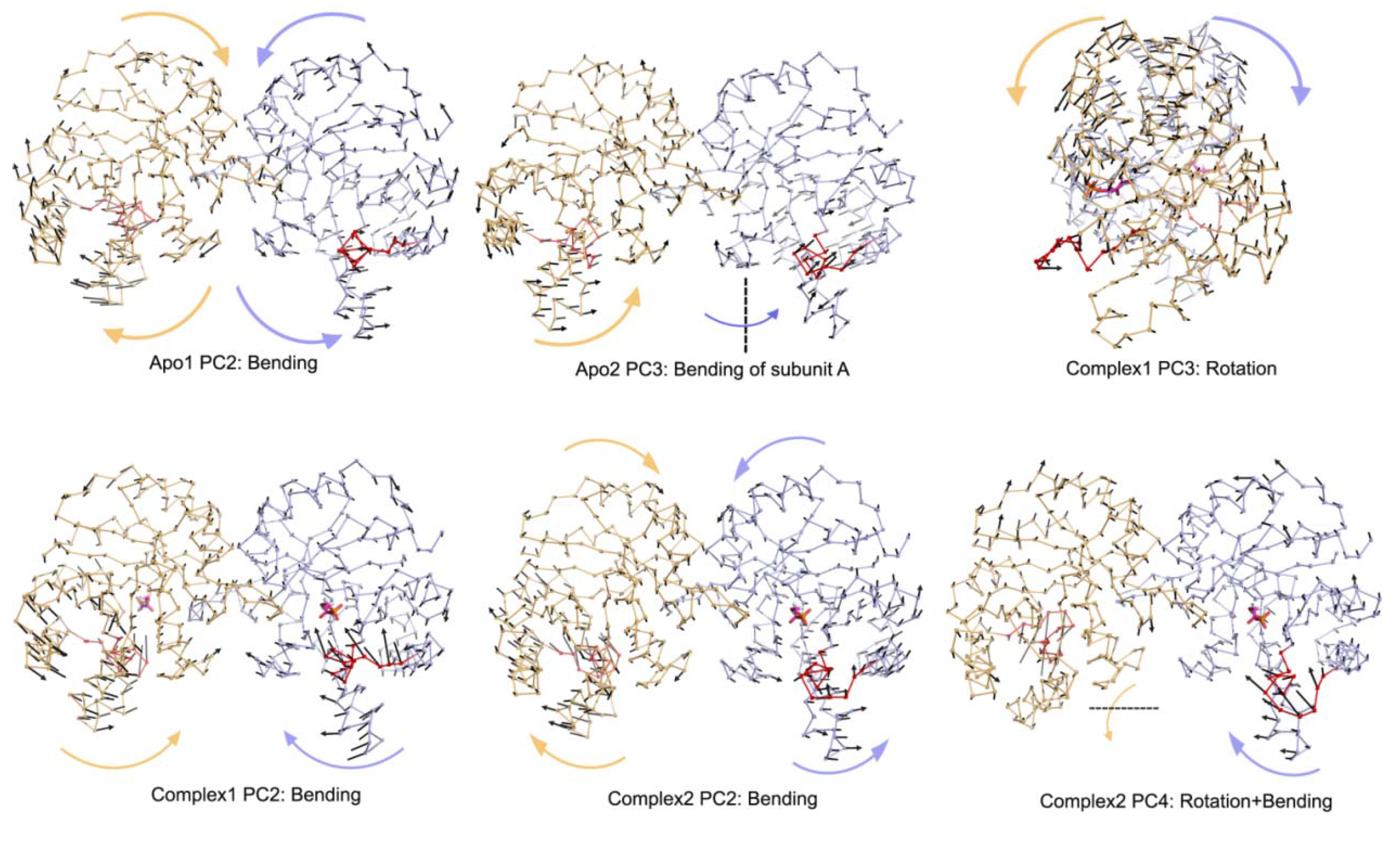
In Complex1, where both DHAP molecules stay bound throughout the simulation, bending of the two subunits with respect to the interface is emphasized in the lower indexed PCs, namely PC1 and PC2. These modes, shown in
Figure 4 and
Figure 5, are coupled to loop opening/closing (see
Table 1). Complex2 with one DHAP (bound to subunit B) represents an intermediate case between apo and Complex1 and this is reflected in its essential modes. Specifically, PC1 and PC2 of the A subunit (without DHAP) exhibit rotation and bending motion, respectively, as in the case of Apo1. In contrast, the PC2 and PC3 for the bound subunit are bending, where loop opening/closure is not observed. PC4 for the same simulation is the combination of these two motions as seen in
Figure 5.
Figure 3.
Distance histograms for I170-Y208, G171-Y208 and T172-Y208 for (a, c, e) apo and (b, d, f) complex simulations, respectively. Distance distribution is obtained by dividing the number of occurrence of the distance to the total number of snapshots for 10–60 ns range.
Figure 3.
Distance histograms for I170-Y208, G171-Y208 and T172-Y208 for (a, c, e) apo and (b, d, f) complex simulations, respectively. Distance distribution is obtained by dividing the number of occurrence of the distance to the total number of snapshots for 10–60 ns range.
Moreover, PC2 of Apo1 simulation corresponds to bending type motion for both subunits and this motion is also observed in PC3 of Apo2 simulation for monomer A only and PC4 of the same simulation for both subunits. From
Table 1, coupling of loop opening/closing motion with bending type motion is not stressed in apo simulations. In summary, the presence of DHAP hinders the coupling of counter-clockwise rotation with loop opening/closing. But loop opening/closing can still be observed in the essential modes, mostly coupled with bending in the presence of two DHAP molecules.
Figure 4.
Most dominant dynamics from PC1 of (a) Apo1, (b) Apo2, (c) Complex1 and (d) Complex2. Subunit A (orange), subunit B (blue) with loop 6 (red) are shown in ribbon and DHAP in magenta-orange stick representation. In (a) and (b), PC1 corresponds to counter-clockwise rotation (CCR) of two subunits, coupled with loop 6 opening/closing. In (c), PC1 of Complex1 simulation is a bending type motion rather than counter-clockwise rotation but loop 6 opening/closing is observed in this mode. In (d), subunit A (without DHAP) rotates like in the Apo1 PC1 coupled with loop opening/closing, whereas a mixed-type of motion is observed in subunit B (with DHAP), where the helix 5 undergoes bending without loop 6 opening/closing.
Figure 4.
Most dominant dynamics from PC1 of (a) Apo1, (b) Apo2, (c) Complex1 and (d) Complex2. Subunit A (orange), subunit B (blue) with loop 6 (red) are shown in ribbon and DHAP in magenta-orange stick representation. In (a) and (b), PC1 corresponds to counter-clockwise rotation (CCR) of two subunits, coupled with loop 6 opening/closing. In (c), PC1 of Complex1 simulation is a bending type motion rather than counter-clockwise rotation but loop 6 opening/closing is observed in this mode. In (d), subunit A (without DHAP) rotates like in the Apo1 PC1 coupled with loop opening/closing, whereas a mixed-type of motion is observed in subunit B (with DHAP), where the helix 5 undergoes bending without loop 6 opening/closing.
Figure 5.
Other PCs for Apo1, Apo2, Complex1 and Complex2 simulations.
Figure 5.
Other PCs for Apo1, Apo2, Complex1 and Complex2 simulations.
Normalized orientational cross-correlations between residue fluctuations (Equation 1) are calculated for apo and complex simulations to observe whether or not DHAP affects the correlations within and between the subunits. The results are averaged over the subunits for the symmetric cases (Apo1-Apo2 and Complex1) and given as intra and inter-subunit maps in
Figure 6. Corresponding maps for each run without averaging over the subunits are given as
supplementary information in
Figure S6. Even though there are some differences, the overall features of Apo1 and Apo2 seem consistent.
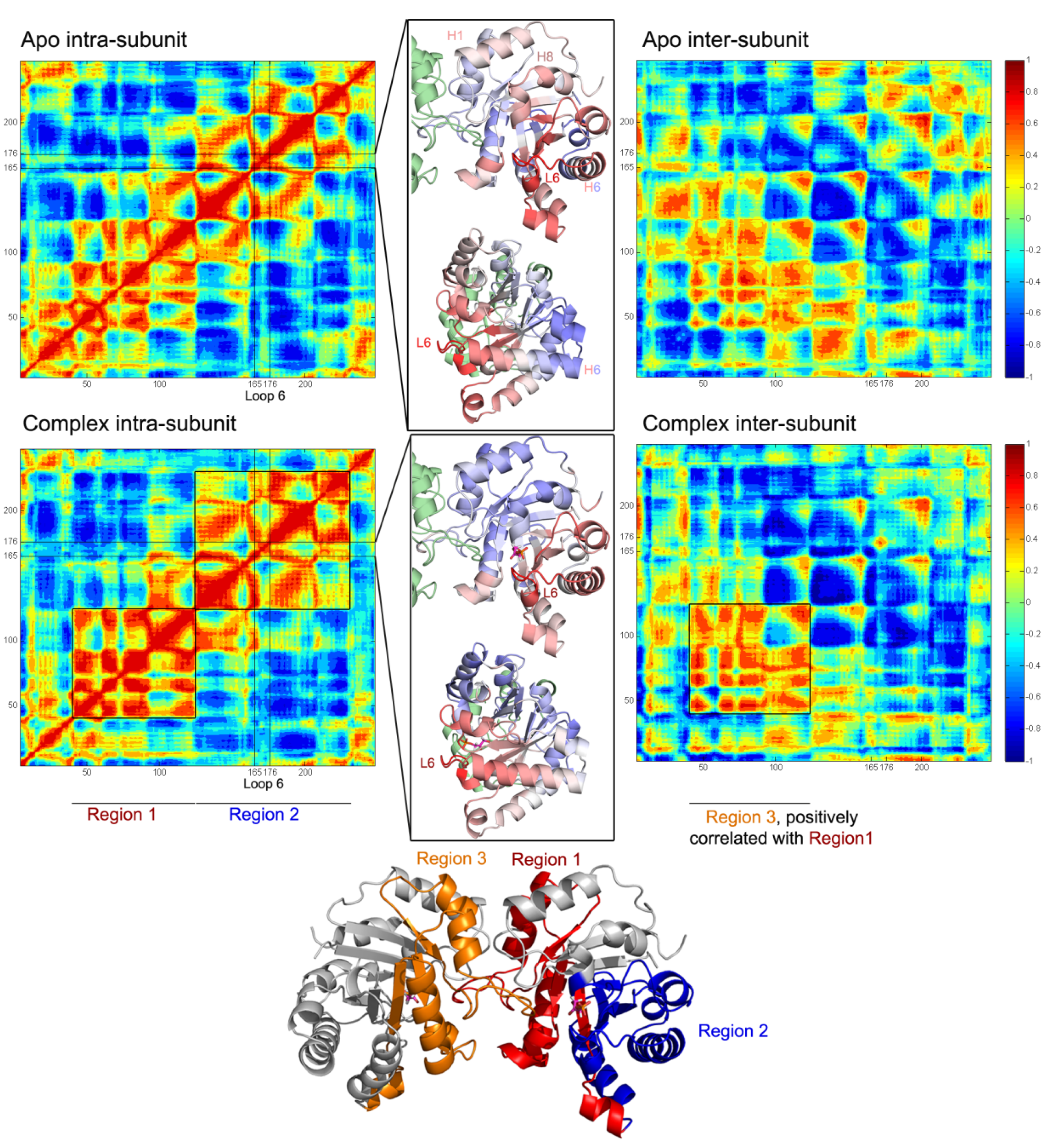
Figure 6.
Normalized orientational cross-correlation maps for apo and complex1. The results for apo are averaged over all the subunits in Apo1 and Apo2 simulations and for complex, over Complex1 A and B subunits. The correlated regions with loop 6 (L6, represented by the average of three tip residues I170, G171, T172) are given in cartoon representations between intra and inter-subunit maps and colored using blue (negative correlation)-white (no correlation)-red (positive correlation) coloring scheme. In the complex intra-subunit map, two blocks- Regions 1 and 2- are negatively correlated with each other. Region 1 is also positively correlated with the same region of the other subunit (named as Region 3) in the inter-subunit map.
Figure 6.
Normalized orientational cross-correlation maps for apo and complex1. The results for apo are averaged over all the subunits in Apo1 and Apo2 simulations and for complex, over Complex1 A and B subunits. The correlated regions with loop 6 (L6, represented by the average of three tip residues I170, G171, T172) are given in cartoon representations between intra and inter-subunit maps and colored using blue (negative correlation)-white (no correlation)-red (positive correlation) coloring scheme. In the complex intra-subunit map, two blocks- Regions 1 and 2- are negatively correlated with each other. Region 1 is also positively correlated with the same region of the other subunit (named as Region 3) in the inter-subunit map.
In general, strong positive and negative correlations are observed both in apo and complex cases. However, presence of DHAP leads to a change in the regions correlated with loop 6, which are shown in blue-white-red color code on the cartoon representations in the middle panels of
Figure 6. Blue and red colors indicate negative and positively correlated regions with loop tip residues, respectively. In apo, loop 6 is correlated with the regions including helix 1 and helix 8, whereas it is anti-correlated with the same regions in the complex. The correlation of loop 6 with helix 6 C-terminus is negative in the absence of DHAP and turns into slightly positive in the complex. These loop 6 correlations are shown in more detail in
Figures S7-S9 for the N-terminus (P166-W168), tip residues (I170-T172) and C-terminus (K174-A176), respectively.
Moreover, a “block” type behavior becomes distinct in the intra-correlations of the complex, where the blocks labeled as “Region 1” and “Region 2” are shown on the cartoon representation of the complex. Region 1 and 2 exhibit clear negative correlations in the intra-subunit map. And in the inter-subunit map, Region 1 shows strong positive correlations with Region 3 (corresponding to Region 1 but on the other subunit). In overall, DHAP presence affects both intra- and inter-subunit correlations in the enzyme.
2.4. Loop Dynamics and Flexibility
To assess the effect of DHAP on loop 6 dynamics, PCA is applied on the loop 6 region only, extracted independently for chains A and B. From
Table 2, loop opening/closing motion is the dominant motion (PC1) in Apo1 (59% and 58% for Apo1 A-B), Complex1 (45%, 58% for A and B, respectively) and Complex2 for A chain (60%). Same motion is observed in the PC2 of Apo2 for both chains (22%, 37% for A and B, respectively) and Complex2 B chain (15%). Lateral movement of the loop is the second dominant motion in Apo1 and Complex1 simulations, and it is PC1 of Apo2 A-B and of the Complex2 B. These two dominant motions of the catalytic loop 6, shown in
Figure 7, do not seem affected from the presence of the DHAP. However there are certain differences in the flexibility of the catalytic loop when DHAP is bound to the catalytic site.
Table 2.
Percentage variance captured by PC modes of loop 6 and overlap with closure direction
Table 2.
Percentage variance captured by PC modes of loop 6 and overlap with closure direction
| | Apo1 | Apo2 | Complex1 | Complex2 |
|---|
| PC | A | B | A | B | A | B | A | B |
| Percentage Variance Captured |
| 1 | 59 | 58 | 45 | 37 | 45 | 58 | 60 | 58 |
| 2 | 21 | 17 | 22 | 29 | 19 | 18 | 16 | 15 |
| Overlap with Closure |
| 1 | 0.79 | 0.71 | 0.09 | 0.12 | 0.68 | 0.73 | 0.84 | 0.03 |
| 2 | 0.03 | 0.49 | 0.83 | 0.75 | 0.51 | 0.06 | 0.15 | 0.75 |
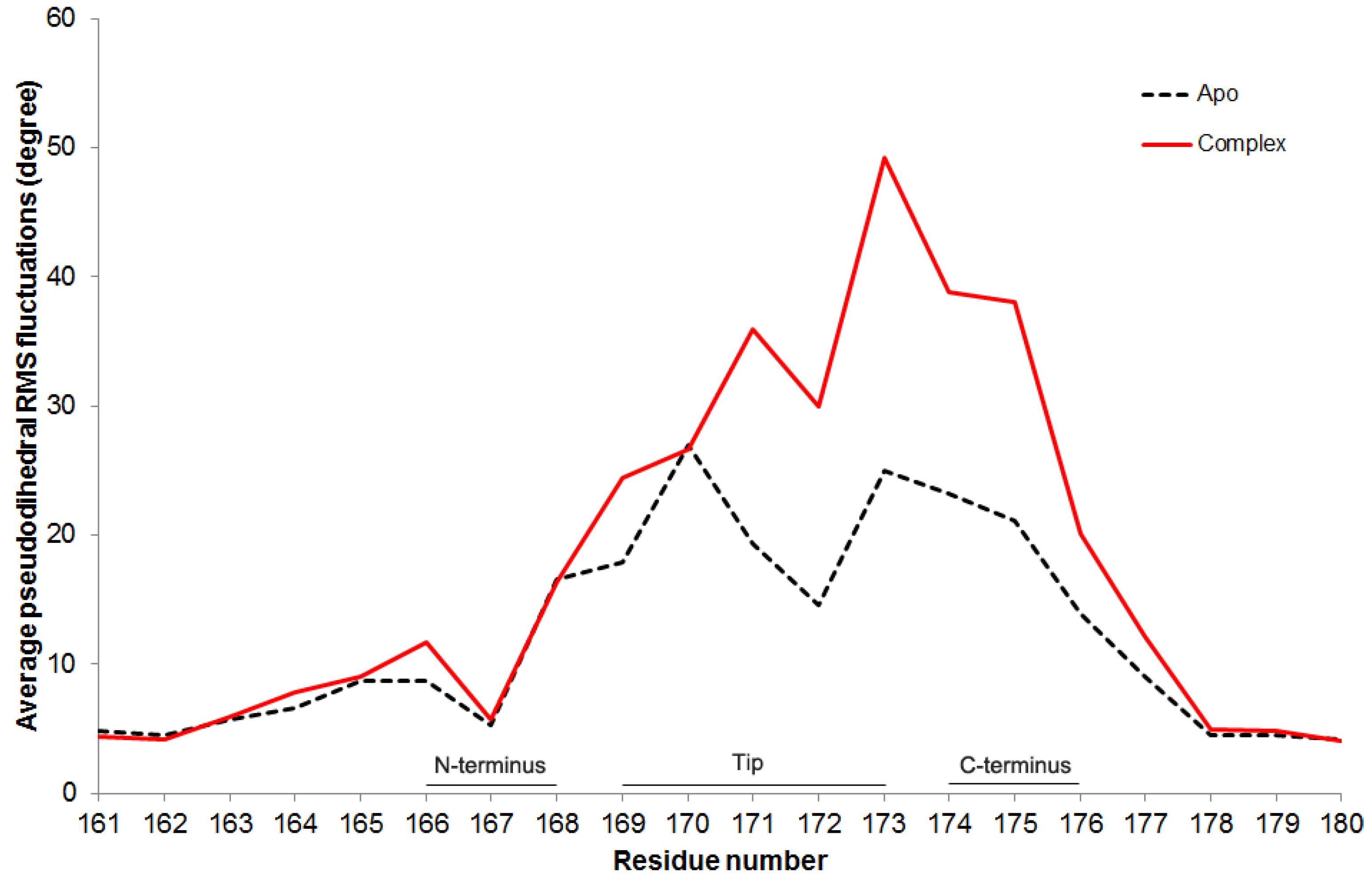
In order to investigate the effect of DHAP molecules on catalytic loop flexibility, the pseudodihedral angle of residue, φ
i, is calculated using C
α coordinates of residues
i−1,
i,
i+1 and
i+2. RMS fluctuations of φ
i for the catalytic loop residues are first calculated for A and B subunits in each run. Then average pseudodihedral RMSF for different subunits and runs are calculated and plotted in
Figure 8. In both apo and complex simulations, residues W168-A176 on the loop 6 are more flexible than the others, which is consistent with the previous findings [
7,
9,
17]. However, when the complex and apo cases are compared with each other, the flexibility increases in the residues P166, A169 and G171-T177 more than 35% in the presence of DHAP.
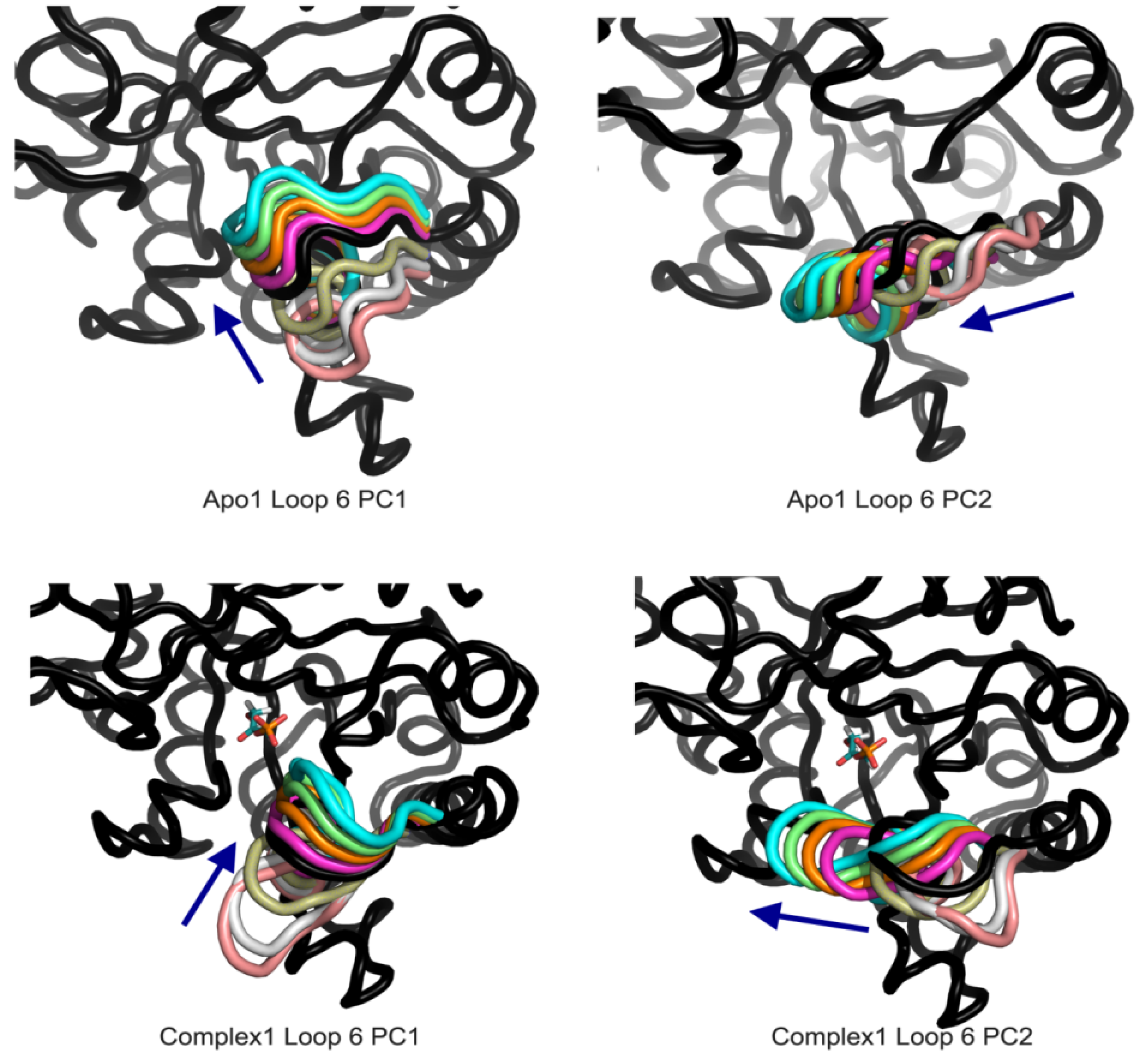
Figure 7.
Apo1 and Complex1 most dominant PCs from loop 6 A PCA. PC1 corresponds to loop opening/closing and PC2 lateral movement of the loop for both simulations.
Figure 7.
Apo1 and Complex1 most dominant PCs from loop 6 A PCA. PC1 corresponds to loop opening/closing and PC2 lateral movement of the loop for both simulations.
Figure 8.
Average pseudodihedral RMS fluctuations for loop 6 residues in apo and complex simulations.
Figure 8.
Average pseudodihedral RMS fluctuations for loop 6 residues in apo and complex simulations.