A Kernel-Based Calculation of Information on a Metric Space

Abstract

Kernel density estimation is a technique for approximating probability distributions. Here, it is applied to the calculation of mutual information on a metric space. This is motivated by the problem in neuroscience of calculating the mutual information between stimuli and spiking responses; the space of these responses is a metric space. It is shown that kernel density estimation on a metric space resembles the k-nearest-neighbor approach. This approach is applied to a toy dataset designed to mimic electrophysiological data.

1. Introduction

This paper is concerned with the calculation of mutual information for spike trains using the data that are available in a typical in vivo electrophysiology experiment in the sensory system. It uses a kernel-based estimation of probability distributions.

In particular, this paper is concerned with computing the mutual information, $I(R;S)$, between two random variables, R and S. The motivating neuroscience example is a typical sensory pathway electrophysiology experiment in which the corpus of sensory stimuli are presented over multiple trials, so there is a set of recorded responses for each of a number of stimuli. The stimuli are drawn from a discrete space, the corpus, but the responses are spike trains. The space of spike trains is peculiar; locally, it is like a smooth manifold, with the spike times behaving like coordinates; but, globally, it is foliated into subspaces, each with a different number of spikes. The space of spike trains does, however, have a metric. As such, S takes values in a discrete set, $\mathcal{S}$, and models the stimulus, and R takes values in a metric space, $\mathcal{R}$, and models the response.

$\mathcal{R}$ is not a discrete space, and so, to calculate the mutual information between S and R, it is necessary to either discretize $\mathcal{R}$ or to use differential mutual information. In the application of information theory to electrophysiological data, it is common to take the former route and discretize the data. Here, the latter alternative is chosen, and the differential mutual information is estimated.

The mutual information between two random variables, R and S, is a measure of the average amount of information that is gained about S from knowing the value of R. With S, a discrete random variable taking values in $\mathcal{S}$ and R, a continuous random variable, the mutual information is:

$${\displaystyle I(R;S)=\sum _{s\in \mathcal{S}}{\int }_{\mathcal{R}}p(r,s){log}_2\frac{p(r,s)}{p\left(r\right)p\left(s\right)}dr}$$

(1)

where $dr$ is the measure on $\mathcal{R}$: computing the differential mutual information between R and S requires integration over $\mathcal{R}$. Integration requires a measure, and when there are coordinates on a space, it is common to use the integration measure derived from these coordinates.

The space of spike trains has no system of coordinates, and so, there is no coordinate-based measure. This does not mean that the space has no measure. As a sample space, it has an intrinsic measure corresponding to the probability distribution; thus, there is a measure, just not one derived from coordinates. The probability of an event occurring in a region of sample space gives a volume for that region. In other words, the volume of a region, $\mathcal{D}$, can be identified with $P(\mathbf{x}\in \mathcal{D})$. This is the measure that will be used throughout this paper; it does not rely on coordinates, and so, can be applied to the case of interest here.

Of course, in practice, the probability density is not usually known on the space of spike trains, but $P(\mathbf{x}\in \mathcal{D})$ can be estimated from the set of experimental data. A Monte-Carlo-like approach is used: the volume of a region is estimated by counting the fraction of data points that lie within it:

$$\mathrm{vol}\left(\mathcal{D}\right)=P(\mathbf{x}\in \mathcal{D})\approx \frac{\text{number of data points in }\mathcal{D}}{\mathrm{total number of points}}$$

(2)

This is exploited in this paper to estimate the volume of square kernels, making it possible to estimate conditional probabilities using kernel density estimation.

The classical approach to the problem of estimating $I(R;S)$ is to map the spike trains to binary words using temporal binning [1,2], giving a histogram approximation for $p(r,s)$. This approach is very successful, particularly when supplemented with a strategically chosen prior distribution for the underlying probability distribution of words [3,4]. This is sometimes called the plug-in method, and that term is adopted here. One advantage of the plug-in method is that the mutual information it calculates is correct in the limit: in the limit of an infinite amount of data and an infinitesimal bin size, it gives the differential mutual information.

Nonetheless, it is interesting to consider other approaches, and in this spirit, an alternate approach is presented here. This new method exploits the inherent metric structure of the space of spike trains, it is very natural and gives an easily implemented algorithm, which is accurate on comparatively small datasets.

2. Methods

This section describes the proposed method for calculating mutual information. Roughly, the conditional probability is approximated using kernel density estimation and, by using the unconditioned probability distribution as a measure, integration is approximated by the Monte-Carlo method of summing over data points.

Since this is a kernel-based approach, a review of kernel density estimation is given in Section 2.1. This also serves to establish notation. The two key steps used to derive the kernel-based estimate are a change of measure and a Monte-Carlo estimate. The change of measure, described in Section 2.2, permits the estimation of probabilities by a simple Monte-Carlo method. The new measure also simplifies the calculation of $I(R;S)$, resulting in a formula involving a single conditional distribution. This conditional distribution is estimated using a Monte-Carlo estimate in Section 2.3.

2.1. Kernel Density Estimation

The non-parametric kernel density estimation (KDE) method [5,6,7] is an approach to estimating probability densities. In KDE, a probability density is estimated by filtering the data with a kernel. This kernel is normalized with an integral of one and is usually symmetric and localized. For an n-dimensional distribution with outcome vectors $\{{\mathbf{x}}_1,{\mathbf{x}}_2,\dots ,{\mathbf{x}}_m\}$ and a kernel, $k\left(\mathbf{x}\right)$, the estimated distribution is usually written:

$$\tilde{p}\left(\mathbf{x}\right)=\frac{1}{m}\sum _{i}k(\mathbf{x}-{\mathbf{x}}_i)$$

(3)

where, because the argument is $\mathbf{x}-{\mathbf{x}}_i$, there is a copy of the kernel centered at each data point. In fact, this relies on the vector-space structure of n-dimensional space; in the application considered here, a more general notation is required, with $k(\mathbf{x};\mathbf{y})$ denoting the value at $\mathbf{x}$ of the kernel when it is centered on $\mathbf{y}$. In this situation, the estimate becomes:

$$\tilde{p}\left(\mathbf{x}\right)=\frac{1}{m}\sum _{i}k(\mathbf{x};{\mathbf{x}}_i)$$

(4)

The square kernel is a common choice. For a vector space, this is:

$$k(\mathbf{x};\mathbf{y})=\left\{\begin{array}{cc}\frac{1}{V}\hfill & \parallel \mathbf{x}-\mathbf{y}\parallel <1\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\right.$$

(5)

where V is chosen, so that the kernel integrates to one. The kernel is usually scaled to give it a bandwidth:

$$k(\mathbf{x};\mathbf{y},h)=\left\{\begin{array}{cc}\frac{1}{hV}\hfill & \parallel \mathbf{x}-\mathbf{y}\parallel <h\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\right.$$

(6)

This bandwidth, h, specifies the amount of smoothing. The square kernel is the most straight-forward choice of kernel mathematically, and so, in the construction presented here, a square kernel is used.

In the case that will be of interest here, where $\mathbf{x}$ and $\mathbf{y}$ are not elements of a vector space, the condition $\parallel \mathbf{x}-\mathbf{y}\parallel <h$ must be replaced by $d(\mathbf{x},\mathbf{y})<h$, where $d(\mathbf{x},\mathbf{y})$ is a metric measuring the distance between $\mathbf{x}$ and $\mathbf{y}$. Calculating the normalization factor, V, is more difficult, since this requires integration. This problem is discussed in the next subsection.

2.2. Change of Measure

Calculating the differential mutual information using KDE requires integration, both the integration required by the definition of the mutual information and the integration needed to normalize the kernel. As outlined above, these integrals are estimated using a Monte-Carlo approach; this relies on a change of measure, which is described in this section.

For definiteness, the notation used here is based on the intended application to spike trains. The number of stimuli is $n_s$, and each stimulus is presented for $n_t$ trials. The total number of responses, $n_r$, is then $n_r=n_s{n}_t$. Points in the set of stimuli are called s and in the response space, r; the actual data points are indexed, $r_i$, and $(r_i,s_i)$ is a response-stimulus pair. As above, the random variables for stimulus and response are S and R, whereas the set of stimuli and the space of responses are denoted by a calligraphic $\mathcal{S}$ and $\mathcal{R}$, respectively. It is intended that when the method is applied, the responses, $r\in \mathcal{R}$, will be spike trains.

The goal is to calculate the mutual information between the stimulus and the response. Using the Bayes theorem, this is:

$$I(R;S)=\sum _{s\in \mathcal{S}}{\int }_{\mathcal{R}}p(r,s){log}_2\frac{p\left(r\right|s)}{p\left(r\right)}dr$$

(7)

Unlike the differential entropy, the differential mutual information is invariant under the choice of measure. Typically, differential information theory is applied to examples where there are coordinates, $(x_1,x_2,\dots ,x_n)$, on the response space and the measure is given by $dr=d{x}_{1}d{x}_2\dots d{x}_n$. However, here, it is intended to use the measure provided by the probability distribution, $p\left(r\right)$. Thus, for a region, $\mathcal{D}\subset \mathcal{R}$, the change of measure is:

$$\mathrm{vol}\left(\mathcal{D}\right)={\int }_{\mathcal{D}}p\left(r\right)dr={\int }_{\mathcal{D}}d\beta$$

(8)

so:

$$d\beta =p\left(r\right)dr$$

(9)

The new probability density relative to the new measure, $p_{\beta }\left(r\right)$, is now one:

$$p_{\beta }\left(r\right)=\frac{p\left(r\right)}{d\beta /dr}=1$$

(10)

Furthermore, since $p\left(r\right|s)$ and $p\left(r\right)$ are both densities, $p\left(r\right|s)/p(r)$ is invariant under a change of measure and:

$$I(R;S)=\sum _s{\int }_{\mathcal{R}}{p}_{\beta }(r,s){log}_2\frac{p_{\beta }\left(r\right|s)}{p_{\beta }\left(r\right)}d\beta =\sum _s{\int }_{\mathcal{R}}{p}_{\beta }(r,s){log}_2{p}_{\beta }\left(r\right|s)d\beta$$

(11)

where, again, $p_{\beta }(r,s)$ and $p_{\beta }\left(r\right|s)$ are the values of the densities, $p(r,s)$ and $p\left(r\right|s)$, after the change of measure.

The expected value of any function, $f(R,S)$, of random variables, R and S, is:

$$\langle f\rangle =\sum _{s\in \mathcal{S}}{\int }_{\mathcal{R}}{p}_{\beta }(r,s)f(r,s)d\beta$$

(12)

and this can be estimated on a set of outcomes, $\left\{(r_i,s_i)\right\}$, as:

$$\langle f\rangle \approx \frac{1}{n_r}\sum _{i}f(r_i,s_i)$$

(13)

For the mutual information, this gives:

$$I(R;S)\approx \frac{1}{n_r}\sum _i{log}_2{p}_{\beta }\left(r_i\right|s_i)$$

(14)

Now, an estimate for $p_{\beta }\left(r_i\right|s_i)$ is needed; this is approximated using KDE.

2.3. A Monte-Carlo Estimate

One advantage to using $d\beta$ as the measure is that $p_{\beta }\left(r\right)=1$, and this simplifies the expression for $I(R;S)$. However, the most significant advantage is that under this new measure, volumes can be estimated by simply counting data points. This is used to normalize the kernel. It is useful to define the support of a function: if $f\left(r\right)$ is a function, then the support of $f\left(r\right)$, supp$\left[f\right(r\left)\right]$, is the region of its domain where it has a non-zero value:

$$\mathrm{supp}\left[f\right(r\left)\right]=\{r:f(r)\ne 0\}$$

(15)

Typically, the size of a square kernel is specified by the radius of the support. Here, however, it is specified by volume. In a vector space where the volume measure is derived from the coordinates, there is a simple formula relating radius and volume. That is not the case here, and specifying the size of a kernel by volume is not equivalent to specifying it by radius. Choosing the volume over the radius simplifies subsequent calculations and, also, has the advantage that the size of the kernel is related to the number of data points. This also means that the radius of the kernel varies across $\mathcal{R}$.

The term, bandwidth, will be used to describe the size of the kernel, even though here, the bandwidth is a volume, rather than a radius. Since $d\beta$ is a probability measure, all volumes are between zero and one. Let h be a bandwidth in this range. If $k(r^{\prime };r,h)$ is the value at $r^{\prime }$ of a square kernel with bandwidth h centered on r, the support will be denoted as $\mathcal{S}(r;h)$:

$$\mathcal{S}(r;h)=\mathrm{supp}\left[k(r^{\prime };r,h)\right]$$

(16)

and the volume of the support of the kernel is vol$\left[\mathcal{S}\right(r;h\left)\right]$. The value of the integral is set at one:

$${\int }_{\mathcal{S}(r;h)}k(r^{\prime };r,h)d\beta =1$$

(17)

and so, since the square kernel is being used, $k(r^{\prime };r,h)$ has a constant value of $1/\text{vol}\left[\mathcal{S}\right(r;h\left)\right]$ throughout $\mathcal{S}(r;h)$.

Thus, volumes are calculated using the measure, $d\beta$, based on the probability density. However, this density is unknown, and so, volumes need to be estimated. As described above, using $d\beta$, the volume of a region is estimated by the fraction of data points that lie within it. In other words, the change of measure leads to a Monte-Carlo approach to calculating the volume of any region. In the Monte-Carlo calculation, the volume of the support of a kernel is estimated as the fraction of data points that lie within it. A choice of convention has to be made between defining the kernel as containing $\lfloor h{n}_r\rfloor$ or $\lceil h{n}_r\rceil$ points, that is, on whether to round $h{n}_r$ down or up. The former choice is used, so, the kernel around a point, r, is estimated as the region containing the nearest $n_h=\lfloor h{n}_r\rfloor$ points to r, including r itself. Thus, the kernel around a point, $r_i$, is defined as:

$$k(r;r_i,n_h)=\left\{\begin{array}{cc}\frac{1}{n_h},\hfill & r\text{ is one of the }{n}_h\mathrm{ closest points to }{r}_i\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(18)

and the support, $\mathcal{S}(r_i;n_h)$, has $r_j\in \mathcal{S}(r_i;n_h)$ if $k(r_j;r_i,n_h)=1/n_h$, or, put another way, $r_j$ is one of the $n_h$ nearest data points. In practice, rather than rounding $h{n}_r$ up or down, the kernel volume in a particular example can be specified using $n_h$ rather than h.

Typically, kernels are balls: regions defined by a constant radius. As such, the kernel described here makes an implicit assumption about the isotropic distribution of the data points. However, in the normal application of KDE, special provision must be made near boundaries, where the distribution of data points is not isotropic [8]. Here, these cases are dealt with automatically.

Since $p_{\beta }\left(r_i\right|s_i)=n_s{p}_{\beta }(r_i,s_i)$, here, the conditional distribution, $p_{\beta }\left(r_i\right|s_i)$, is estimated by first estimating $p_{\beta }(r_i,s_i)$. As described above, a kernel has a fixed volume relative to the measure based on $p_{\beta }\left(r\right)$. Here, the kernel is being used to estimate $p_{\beta }(r_i,s_i)$:

$${\tilde{p}}_{\beta }(r_i,s_i)=\frac{c(r_i,s_i;n_h)}{n_h}$$

(19)

where $c(r_i,s_i;n_h)$ is the number of data points evoked to stimulus $s_i$ for which $r_i$ is one of the $n_h$ closest points:

$$c(r_i,s_i;n_h)=\left|\{(r_j,s_i):r_j\in \mathcal{S}(r_i;n_h)\}\right|$$

(20)

This gives the estimated mutual information:

$$I(R;S)\approx I(R,S;n_h)=\frac{1}{n_r}\sum _i{log}_2\frac{n_{s}c(r_i,s_i;n_h)}{n_h}$$

(21)

Remarkably, although this is a KDE estimator, it resembles a k-, or, here, $n_h$-, nearest-neighbors estimator. Basing KDE on the data available for spike trains appears to lead naturally to nearest neighbor estimation.

The formula for $I(R,S;n_h)$ behaves well in the extreme cases. If the responses to each stimulus are close to each other, but distant from responses to all other stimuli, then $c(r_i,s_i;n_h)=n_h$ for all stimulus-response pairs $(r_i,s_i)$. That is, for each data point, all nearby data points are from the same stimulus. This means that the estimate will be:

$$I(R,S;n_h)={log}_2{n}_s$$

(22)

This is the correct value, because, in this case, the response completely determines the stimulus, and so, the mutual information is exactly the entropy of the stimulus. On the other hand, if the responses to each stimulus have the same distribution, then $c(r_i,s_i;n_h)/n_h\approx 1/n_s$, so the estimated mutual information will be close to zero. This is again the correct value, because in this case, the response is independent of the stimulus.

3. Results

As a test, this method has been applied to a toy dataset modelled on the behavior of real spike trains. It is important that the method is applied to toy data that resemble the data type, electrophysiological data, on which the method is intended to perform well. As such, the toy model is selected to mimic the behavior of sets of spike trains. The formula derived above acts on the matrix of inter-data-point distances, rather than the points themselves, and so, the dataset is designed to match the distance distribution observed in real spike trains [9]. The test dataset is also designed to present a stiff challenge to any algorithm for estimating information.

The toy data are produced by varying the components of one of a set of source vectors. More precisely, to produce a test dataset, a variance, ${\sigma }^2$, is chosen uniformly from $[0,1]$, and $n_s$ sources are chosen uniformly in a $n_d$-dimensional box centered at the origin with unit sides parallel to the Cartesian axes. Thus, the sources are all $n_d$-dimensional vectors. The data points are also $n_d$-dimensional vectors; they are generated by drawing each component from a normal distribution about the corresponding component of the source. Thus, data points with a source $\mathbf{s}=(s_1,s_2,\dots ,s_{n_d})$ are chosen as $\mathbf{r}=(r_1,r_2,\dots ,r_{n_d})$, where the $r_i$ are all drawn from normal distributions with variance ${\sigma }^2$ centered at the corresponding $s_i$:

$$r_i\sim \mathcal{N}(s_i,{\sigma }^2)$$

(23)

$n_t$ data points are chosen for each source, giving $n_r=n_s{n}_t$ data points in all.

Each test uses 200 different datasets; random pruning is used to ensure that the values of mutual information are evenly distributed over the whole range from zero to ${log}_2{n}_s$; otherwise, there tends to be an excess of datasets with a low value. The true mutual information is calculated using a Monte-Carlo estimate sampled over 10,000 points. The actual probability distributions are known: the probability of finding a point $\mathbf{r}$ generated by a source, $\mathbf{s}$, depends only on the distance $d=|\mathbf{r}-\mathbf{s}|$ and is given by the χ-distribution:

$$p\left(d\right)=\frac{2^{1-n_d/2}}{\Gamma (n_d/2)}{\left(\frac{d}{\sigma }\right)}^{n_d-1}{e}^{-d^2/2{\sigma }^2}$$

(24)

There is a bias in estimating the mutual information, in fact, bias is common to any approach to estimating mutual information [10]. The problem of reducing bias, or defining the mutual information, so that the amount of bias is low, is well studied and has produced a number of sophisticated approaches [4,10,11,12,13,14]. One of these, quadratic estimation, thanks to [11,13], is adapted to the current situation. Basically, it is assumed that for large numbers of data points, $n_t$, the estimated information, $\tilde{I}(R;S)$, is related to the true mutual information $I(R;S)$ by:

$$\tilde{I}(R;S)=I(R;S)+\frac{A}{n_t}+\frac{B}{n_t^2}+O(1/n_t^3)$$

(25)

This asymptotic expansion is well-motivated in the case of the plug-in approach to spike train information [10,11,15,16,17], and since the sources of bias are presumably similar, it is assumed the same expansion applies. In fact, this assumption is supported by plots of $I(R,S;n_h)$ against $n_t$. To extract $I(R;S)$, the estimate, $I(R,S;n_h)$, is calculated for $\lambda n_r$ with λ taking values from 0.1 to one in 0.1 increments. Least squares fit is used to estimate $I(R;S)$ from these ten values.

The new method works well on these toy data. It is compared to a histogram approach, where the $n_d$-dimensional space is discretized into bins and counting is used to estimate the probability of each bin. This is an analog of the plug-in method, and the same quadratic estimation technique is used to reduce bias.

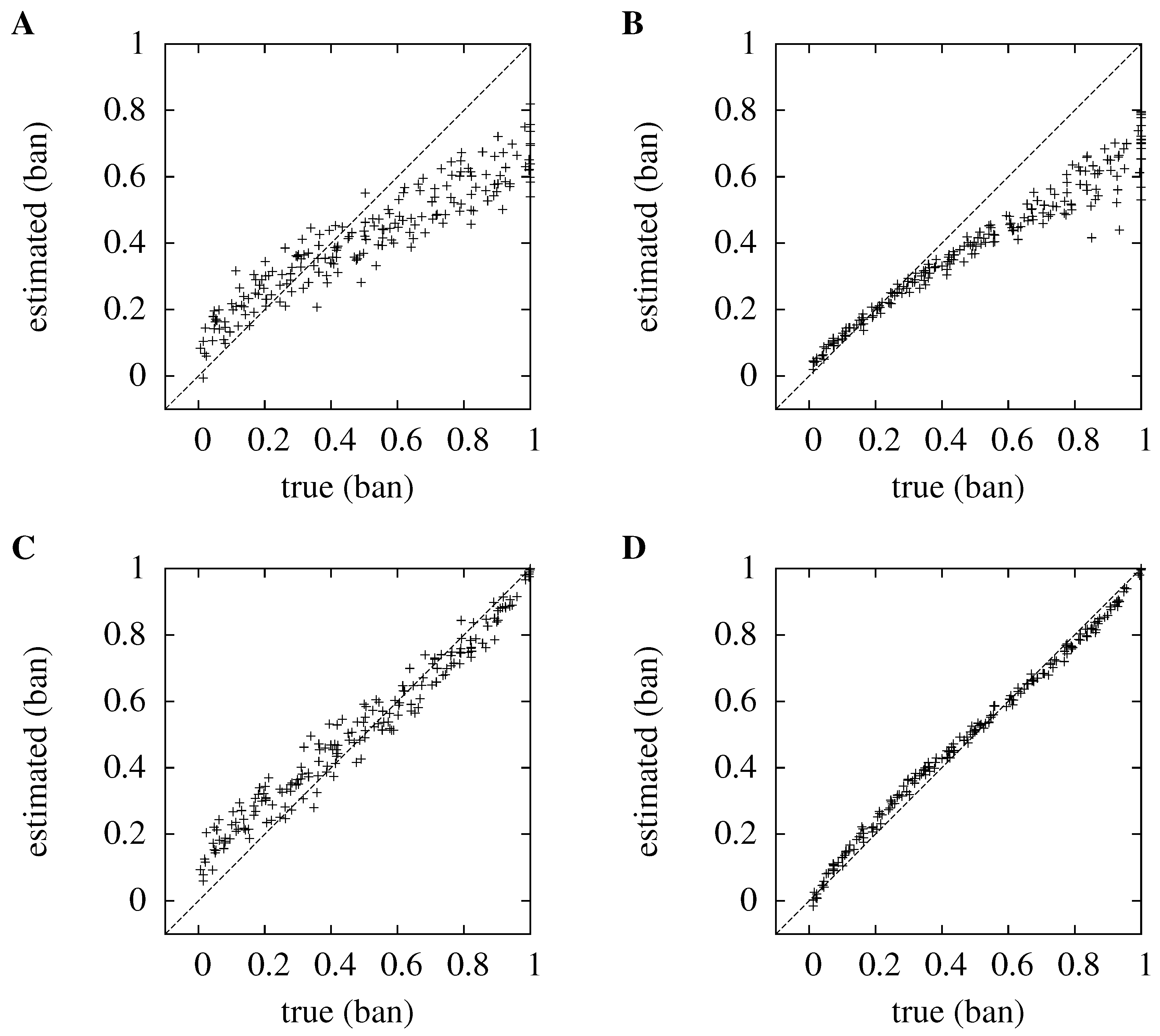
Figure 1. Comparing kernel density estimation (KDE) to the histogram method for ten sources, $n_s=10$, and three dimensions, $n_d=3$. In each case, the true information is plotted against the estimated information; the line, $y=x$, which represents perfect estimation, is plotted for clarity. For convenience, the mutual information has been normalized, so in each case, the value plotted is the estimate of $I(R;S)/{log}_2{n}_s$, with a maximum value of one; in the cases plotted here, that means the information is measured in ban. (A) and (B) show the distribution for the histogram method for $n_t=10$ and $n_t=200$; (C) and (D) show the kernel method.

Figure 1. Comparing kernel density estimation (KDE) to the histogram method for ten sources, $n_s=10$, and three dimensions, $n_d=3$. In each case, the true information is plotted against the estimated information; the line, $y=x$, which represents perfect estimation, is plotted for clarity. For convenience, the mutual information has been normalized, so in each case, the value plotted is the estimate of $I(R;S)/{log}_2{n}_s$, with a maximum value of one; in the cases plotted here, that means the information is measured in ban. (A) and (B) show the distribution for the histogram method for $n_t=10$ and $n_t=200$; (C) and (D) show the kernel method.

In Figure 1, the new method is compared to the histogram method when $n_s=10$ and $n_d=3$, and for both low and high numbers of trials, $n_t=10$ and $n_t=200$. For the histogram method, the optimum discretization width is used. This optimal width is large, $h=5$ in each case; this roughly corresponds to a different bin for each octant of the three-dimensional space containing the data. In the new method, the bandwidth is not optimized on a case by case basis; instead, the kernel bandwidth, $n_h$, is chosen as being equal to the number of trials, $n_t$. It can be seen that the new method is better at estimating the information: for $n_t=10$, it has an average absolute error of $0.189$ bits, compared to $0.481$ bits for the histogram method; for $n_t=200$, the average absolute error is $0.083$ bits, compared to $0.442$ bits for the histogram approach.

Figure 2. Comparing the KDE to the histogram method for high and low numbers of sources and dimensions. The true information is plotted against the estimated information; in (A) and (C), $n_s=10$ and $n_d=10$; in (B) and (D), $n_s=3$ and $n_d=3$. The top row, (A) and (B), is for the histogram method, the bottom row, (C) and (D), is for the kernel method. As before, the normalized information, $I(S;R)/{log}_2{n}_s$, is plotted. So, for $n_s=10$, the information is in ban, for $n_s=3$, in trit, and in each case, the maximum mutual information is one. $n_r=200$ for all graphs.

Figure 2. Comparing the KDE to the histogram method for high and low numbers of sources and dimensions. The true information is plotted against the estimated information; in (A) and (C), $n_s=10$ and $n_d=10$; in (B) and (D), $n_s=3$ and $n_d=3$. The top row, (A) and (B), is for the histogram method, the bottom row, (C) and (D), is for the kernel method. As before, the normalized information, $I(S;R)/{log}_2{n}_s$, is plotted. So, for $n_s=10$, the information is in ban, for $n_s=3$, in trit, and in each case, the maximum mutual information is one. $n_r=200$ for all graphs.

In Figure 2, the histogram and kernel methods are compared for $n_s=10$ and $n_d=10$ and for $n_s=3$ and $n_d=3$; the number of trials is $n_t=200$ in each case. The kernel method outperforms the histogram method. When $n_s=10$ and $n_d=10$, the average absolute error for the kernel method is 0.139 bits, compared to 0.876 bits for the histogram method; for $n_s=3$ and $n_d=3$, its average absolute error is 0.076 bits compared to 0.141 bits for the histogram. Furthermore, the errors for the kernel method are less clearly modulated by the actual information, which makes the method less prone to producing misleading results.

4. Discussion

Although the actual method presented here is very different, it was inspired in part by the transmitted information method for calculating mutual information using metric-based clustering described in [18] and by the novel approach introduced in [19], where a kernel-like approach to mutual information is developed. Another significant motivation was the interesting technique given in [20], where the information is estimated by measuring how large a sphere could be placed around each data point without it touching another data point. In [20], the actual volume of the sphere is required, or, rather, the rate the volume changes with diameter. This is calculated by foliating the space of spike trains into subspaces with a fixed spike number and interpreting the spike times as coordinates. This is avoided here by using the Monte-Carlo estimate of volumes. Finally, the copula construction is related to the approach described here. In fact, the construction here can be thought of as a reverse copula construction [21].

An important part of the derivation of the kernel method is the change of measure to one based on the distribution. Since the kernel size is defined using a volume based on this measure, the radius of the kernel adapts to the density of data points. This is similar to the adaptive partitioning described, for example, in [22]. Like the plug-in method of computing mutual information for spike trains, adaptive partitioning is a discretization approach. However, rather than breaking the space into regions of fixed width, the discrete regions are chosen dynamically, using estimates of the cumulative distribution, similar to what is proposed here.

One striking aspect of KDE seen here is that it reduces to a kth nearest-neighbor (kNN) estimator. The kNN approach to estimating the mutual information of variables lying in metric spaces has been studied directly in [23]. Rather than using a KDE of the probability distribution, a Kozachenko-Leonenko estimator [24] is used. To estimate $I(X;Y)$, where X and Y are both continuous random variables taking values in $\mathcal{X}$ and $\mathcal{Y}$, Kozachenko-Leonenko estimates are calculated for $H\left(X\right)$, $H\left(Y\right)$ and $H(X,Y)$; by using different values of k in each space, the terms that would otherwise depend on the dimension of $\mathcal{X}$ and $\mathcal{Y}$ cancel.

This approach can be modified to estimate $I(R;S)$, where S is a discrete random variable. Using the approach described in [23] to estimate $H\left(R\right)$ and $H\left(R\right|S)$ gives:

$${\displaystyle I_e(R;S)\approx ϝ\left(n_k\right)+ϝ\left(n_t{n}_s\right)-ϝ\left(n_t\right)-\frac{1}{n_r}\sum _iϝ\left[C(r_i,s_i;n_k)\right]}$$

(26)

where $ϝ\left(x\right)$ is the digamma function, $n_k$ is an integer parameter and $C(r_i,s_i;n_k)$ is similar to $c(r_i,s_i;n_h)$ above. Whereas $c_k(r_i,s_i;n_h)$ counts the number of responses to $s_i$ for which $r_i$ is one of the $n_h$ closest data points, $C(r_i,s_i;n_k)$ is computed by first finding the distance, d, from $r_i$ to the $n_k$th nearest spike-train response to stimulus $s_i$; then, $C(r_i,s_i;n_k)$ counts the number of spike trains, from any stimulus, that is at most a distance of d from $r_i$. $I_e(R;S)$ is the mutual information with base e, so $I(R;S)=I_e(R;S)/ln2$. During the derivation of this formula, expressions involving the dimension of $\mathcal{S}$ appear, but ultimately, they all cancel, leaving an estimate which can be applied in the case of interest here, where $\mathcal{S}$ has no dimension. Since the digamma function can be approximated as:

$$ϝ\left(x\right)\approx lnx-\frac{1}{2x}$$

(27)

for large x, this kNN approach and the kernel method produce very similar estimates. The similarity between the two formulas, despite the different routes taken to them, lends credibility to both estimators.

Other versions of the kernel method can be envisaged. A kernel with a different shape could be used or the kernel could be defined by the radius rather than by the volume of the support. The volume of the support and, therefore, the normalization would then vary from data point to data point. This volume could be estimated by counting, as it was here. However, as mentioned above, the volume-based bandwidth has the advantage that it gives a kernel that is adaptive: the radius varies as the density of data points changes. Another intriguing possibility is to investigate if it would be possible to follow [20] and [23] more closely than has been done here and use a Monte-Carlo volume estimate to derive a Kozachenko and Leonenko estimator. Finally, KDE applied to two continuous random variables could be used to derive an estimate for the mutual information between two sets of spike trains or between a set of spike trains and a non-discrete stimulus, such as position in a maze.

There is no general, principled approach to choosing bandwidths for KDE methods. There are heuristic methods, such as cross-validation [25,26], but these include implicit assumptions about how the distribution of the data is itself drawn from a family of distributions, assumptions that may not apply to a particular experimental situation. The KDE approach developed here includes a term analogous to bandwidth, and although a simple choice of this bandwidth is suggested and gives accurate estimates, the problem of optimal bandwidth selection will require further study.

Applying the KDE approach to spike trains means it is necessary to specify a spike train metric [18,27,28]. Although the metric is only used to arrange points in the order of proximity, the dependence on a metric does mean that the estimated mutual information will only include mutual information encoded in features of the spike train that affect the metric. As described in [20], in the context of another metric-dependent estimator of mutual information, this means the mutual information may underestimate the true mutual information, but it does allow the coding structure of spike trains to be probed by manipulating the spike train metrics.

It is becoming increasingly possible to measure large number spike trains from large numbers of spike trains simultaneously. There are metrics for measuring distances between sets of multi-neuron responses [29,30,31], and so, the approach described here can also be applied to multi-neuronal data.