The Fractional Differential Polynomial Neural Network for Approximation of Functions
Abstract
:1. Introduction
2. Preliminaries




3. Results
3.1. Proposed Method




| Data | Actual Value | Approximate Value | Absolute Error |
|---|---|---|---|
| (1,0) | 1 | 0.25 | |
| 0.25 | |||
| (0,1) | 1 | 0.25 | |
| 0.25 | |||
| (1,1) | 1 | 0.5 | |
| 0.3 | |||
| 0.1 | |||
| 0.01 | |||
| (1/2,1/2) | 1 | 0.66 | |
| 0.6 | |||
| 0.57 | |||
| 0.53 | |||
| 0.4 |


| Data | Actual Value | Approximate Value | Absolute Error |
|---|---|---|---|
| (1,0,0) | 1 | 0.5 | |
| 0.5 | |||
| (0,1,0) | 1 | 0.5 | |
| 0.5 | |||
| (0,0,1) | 1 | 0 | |
| (1,1,0) | 1 | 0.125 | |
| 0.025 | |||
| 0.12 | |||
| 0.063 | |||
| (1,0,1) | 1 | 0.5 | |
| 0.368 | |||
| 0.249 | |||
| 0.1 | |||
| (1,1,1) | 1 | 0.6 | |
| 0.488 | |||
| 0.26 | |||
| 0.0755 |



3.2. Modified Information Theory
| Data | Actual Value | Approximate Value | Absolute Error |
|---|---|---|---|
| (1,0) | 2 | 0 | |
| 0.166 | |||
| 0.319 | |||
| 0.4577 | |||
| (0,1) | 2 | 0 | |
| 0.166 | |||
| 0.319 | |||
| 0.4577 | |||
| (1,1) | 2 | 0.49 | |
| 0.04 | |||
| 0.335 | |||
| 0.633 |
4. Discussion
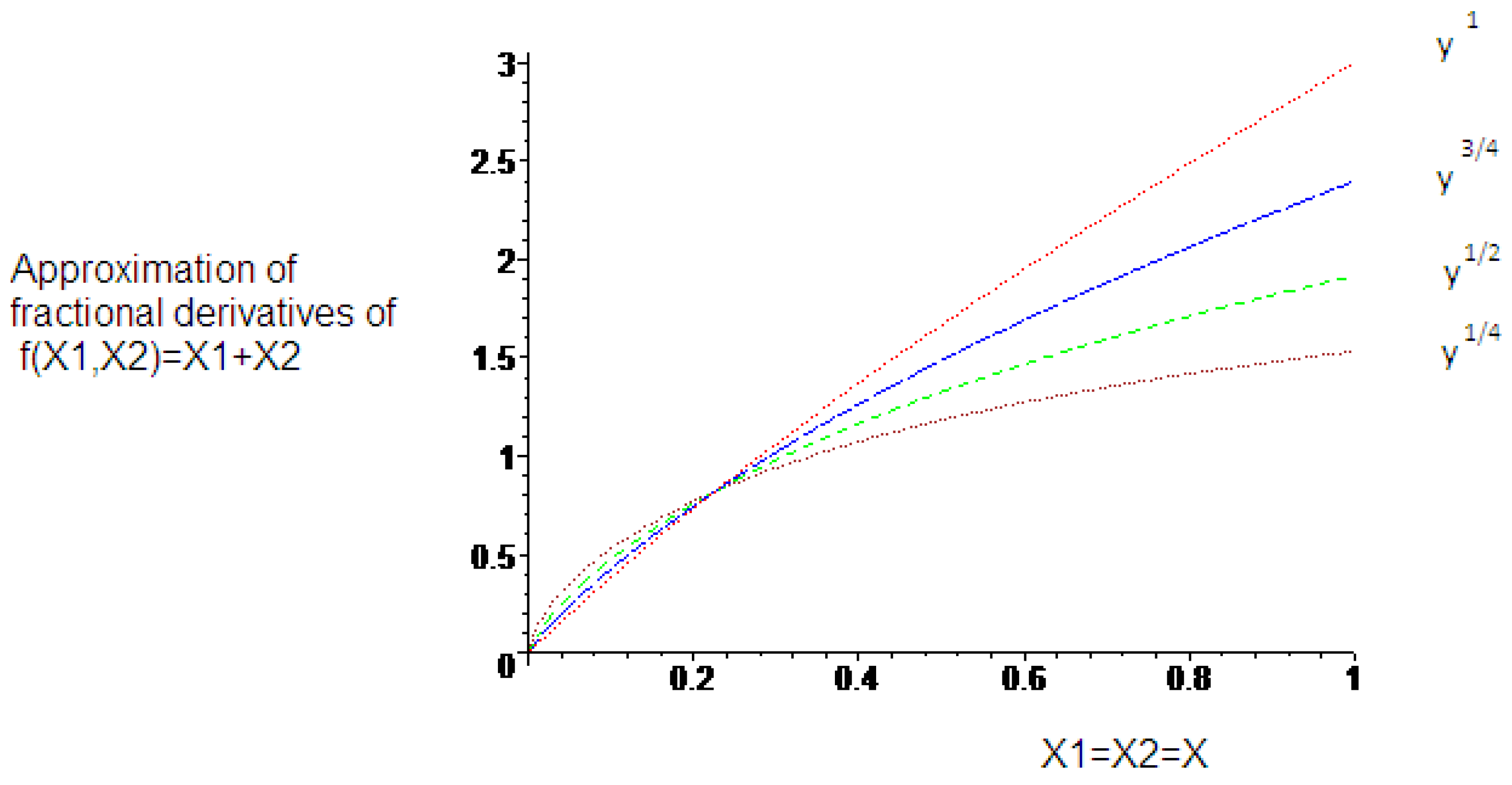
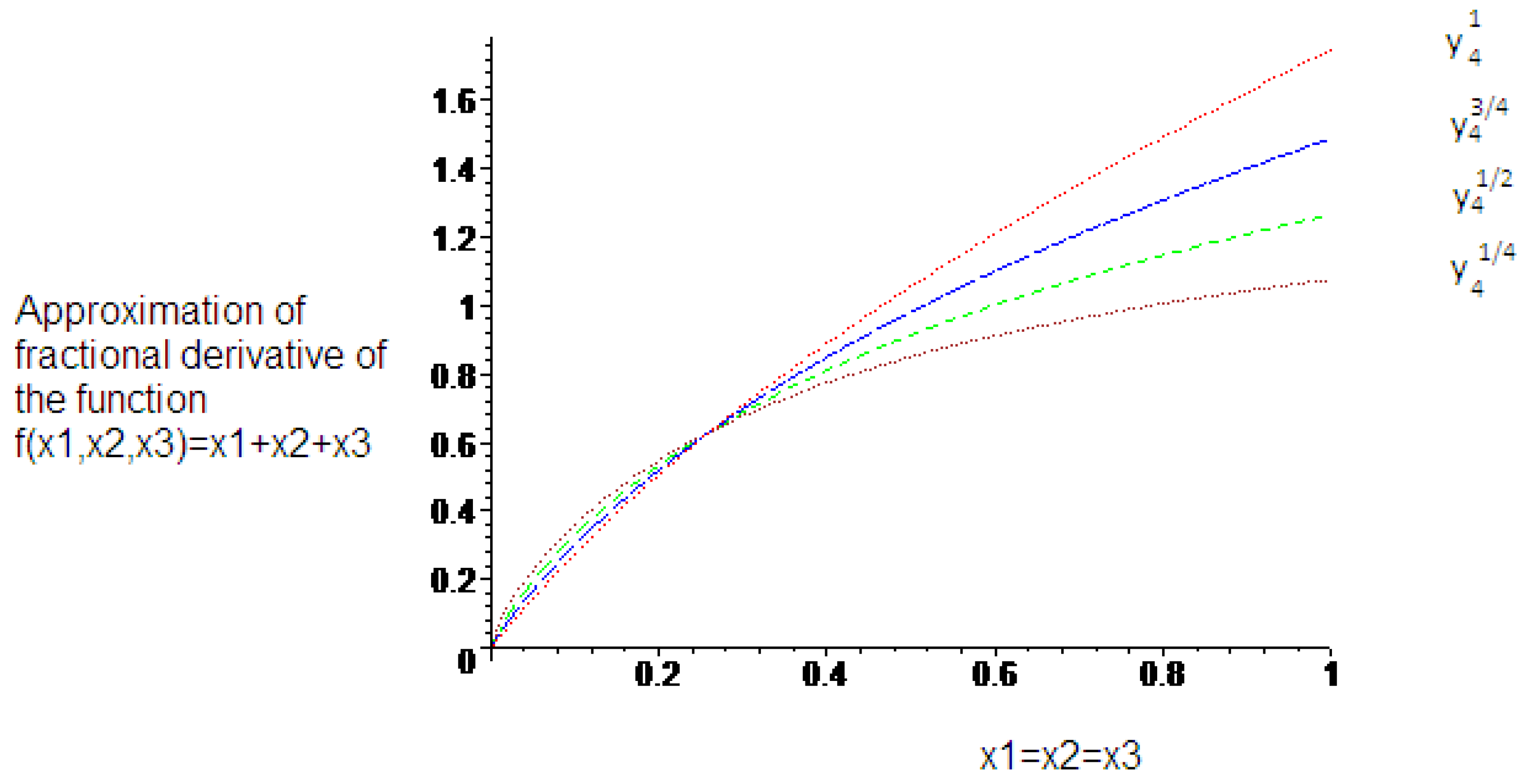

5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Zjavka, L. Generalization of patterns by identification with polynomial neural network. J. Elec. Eng. 2010, 61, 120–124. [Google Scholar] [CrossRef]
- Zjavka, L. Construction and adjustment of differential polynomial neural network. J. Eng. Comp. Inn. 2011, 2, 40–50. [Google Scholar]
- Zjavka, L. Recognition of generalized patterns by a differential polynomial neural network. Eng. Tech. Appl. Sci. Res. 2012, 2, 167–172. [Google Scholar]
- Zjavka, L. Approximation of multi-parametric functions using the differential polynomial neural network. Math. Sci. 2013, 7, 1–7. [Google Scholar] [CrossRef]
- Giles, C.L. Noisy time series prediction using recurrent neural networks and grammatical inference. Machine Learning 2001, 44, 161–183. [Google Scholar] [CrossRef]
- Tsoulos, I.; Gavrilis, D.; Glavas, E. Solving differential equations with constructed neural networks. Neurocomputing 2009, 72, 2385–2391. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Hilfer, R. Application of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- West, B.J.; Bologna, M.; Grigolini, P. Physics of Fractal Operators; Academic Press: New York, NY, USA, 2003. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherland, 2006. [Google Scholar]
- Sabatier, J.; Agrawal, O.P.; Machado, T. Advance in Fractional Calculus: Theoretical Developments and Applications in Physics and Engineering; Springer: London, UK, 2007. [Google Scholar]
- Lakshmikantham, V.; Leela, S.; Devi, J.V. Theory of Fractional Dynamic Systems; Cambridge Scientific Pub.: Cambridge, UK, 2009. [Google Scholar]
- Jalab, J.A.; Ibrahim, R.W. Stability of recurrent neural networks. Int. J. Comp. Sci. Net. Sec. 2006, 6, 159–164. [Google Scholar]
- Gardner, S. Exploring fractional order calculus as an artifficial neural network augmentation. Master’s Thesis, Montana State University, Bozeman, Montana, April 2009. [Google Scholar]
- Almarashi, A. Approximation solution of fractional partial differential equations by neural networks. Adv. Numer. Anal. 2012, 2012, 912810. [Google Scholar] [CrossRef]
- Jalab, H.A.; Ibrahim, R.W.; Murad, S.A.; Hadid, S.B. Exact and numerical solution for fractional differential equation based on neural network. Proc. Pakistan Aca. Sci. 2012, 49, 199–208. [Google Scholar]
- Zhou, S.; Cao, J.; Chen, Y. Genetic algorithm-based identification of fractional-order systems. Entropy 2013, 15, 1624–1642. [Google Scholar] [CrossRef]
- Chen, L.; Qu, J.; Chai, Y.; Wu, R.; Qi, G. Synchronization of a class of fractional-order chaotic neural networks. Entropy 2013, 15, 3265–3276. [Google Scholar] [CrossRef]
- Ivachnenko, A.G. Polynomial Theory of Complex Systems. IEEE Trans. Sys. Man Cyb. 1971, 4, 364–378. [Google Scholar] [CrossRef]
- Kolwankar, K.M.; Gangal, A.D. Fractional differentiability of nowhere differentiable functions and dimensions. Chaos 1996, 6, 505–513. [Google Scholar] [CrossRef] [PubMed]
- Adda, F.B.; Cresson, J. About non-differentiable functions. J. Math. Anal. Appl. 2001, 263, 721–737. [Google Scholar] [CrossRef]
- Odibat, Z.M.; Shawagfeh, N.T. Generalized Taylor’s formula. Appl. Math. Comp. 2007, 186, 286–293. [Google Scholar] [CrossRef]
- Freed, A.; Diethelm, K.; Luchko, Y. Fractional-order viscoelasticity (FOV): Constitutive development using the fractional calculus. In First Annual Report NASA/TM-2002-211914; NASA's Glenn Research Center: Cleveland, OH, USA, 2002. [Google Scholar]
- Gorenflo, R.; Loutchko, J.; Luchko, Y. Computation of the Mittag-Leffler function Eα,β(z) and its derivative. Frac. Calc. Appl. Anal. 2002, 5, 491–518. [Google Scholar]
- Podlubny, I. Mittag-Leffler function, The MATLAB routine. http://www.mathworks.com/matlabcentral/fileexchange (accessed on 25 March 2009).
- Seybold, H.J.; Hilfer, R. Numerical results for the generalized Mittag-Leffler function. Frac. Calc. Appl. Anal. 2005, 8, 127–139. [Google Scholar]
- Ibrahim, R.W. Fractional complex transforms for fractional differential equations. Adv. Diff. Equ. 2012, 192, 1–11. [Google Scholar] [CrossRef]
- Casasanta, G.; Ciani, D.; Garra, R. Non-exponential extinction of radiation by fractional calculus modelling. J. Quan. Spec. Radi. Trans. 2012, 113, 194–197. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, Volume, 379–423. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ibrahim, R.W. The Fractional Differential Polynomial Neural Network for Approximation of Functions. Entropy 2013, 15, 4188-4198. https://doi.org/10.3390/e15104188
Ibrahim RW. The Fractional Differential Polynomial Neural Network for Approximation of Functions. Entropy. 2013; 15(10):4188-4198. https://doi.org/10.3390/e15104188
Chicago/Turabian StyleIbrahim, Rabha W. 2013. "The Fractional Differential Polynomial Neural Network for Approximation of Functions" Entropy 15, no. 10: 4188-4198. https://doi.org/10.3390/e15104188






