1. Introduction
Two of the most basic concepts of thermodynamics are: (a) the average of measurement outcomes and (b) the uncertainty or entropy about measurement outcomes. Consider, for example, a physical system, A, that is in contact with a heat bath at some fixed temperature, i.e., a canonical ensemble. The measurement of the system’s energy can return any one of its energy eigenstates. What then is (a) the mean energy to expect and (b) how uncertain is the prediction of the measured energy state?
We notice that, in principle, many different notions of energy mean and many different measures of entropy could be employed here. Of course, in thermodynamics, the Boltzmann factor weighted
mean as well as the Shannon/von Neumann
entropy are of foremost importance. In this paper, we show that also other important notions of average such as the harmonic mean, the geometric mean and the arithmetic mean arise naturally, along with generalized notions of entropy including Rényi entropies [
1], all unified in a two-parameter family of notions of means and notions of entropies.
To this end, consider systems (canonical ensembles) in a heat bath. We begin by considering the simplest kind of system, namely the type of system which possesses only one energy level, E. Let us denote its degeneracy by k. Unambiguously, we should assign that system the mean and the entropy . Let us denote these simple one-level systems by the term reference system.
Now, let X be a system with arbitrary discrete energy levels. Our aim is to assign X a mean and an entropy by finding that reference system M which is in some sense equivalent to X. Then we assign X the same value for the mean and entropy as the reference system M.
But how do we decide if a reference system is in some sense equivalent to system X? Given that we want the reference system M and system X to share two properties, namely a mean and an entropy, we expect any such condition for the equivalence of two systems to require two equations to be fulfilled. Further, since the properties of systems are encoded in their partition function , we expect that these two equations can be expressed in terms of the partition functions of the two systems in question.
To this end, let us adopt what may be considered the simplest definition. We choose two temperatures, T1 and T2 and we define that a reference system is (T1, T2)-equivalent to system X if the partition functions of the two systems coincide with each other at these two temperatures. Since the Helmholtz free energy obeys , where is the Boltzmann constant, this is the same as saying that two systems are put in the same equivalence class if their Helmholtz free energies coincide at these two temperatures.
This allows us now to assign any system X a mean and an entropy. We simply find its unique (T1 and T2)-equivalent reference system M. Then the mean and entropy of X are defined to be the mean and the entropy of the reference system M.
Clearly, the so-defined mean and entropy of a system X now actually depend on two temperatures, namely (T1, T2). As we will show below, in the limit when we let the two temperatures become the same temperature, we recover the usual Boltzmann factor-weighted mean, i.e., the usual mean energy, along with the usual Shannon/von Neumann entropy.
For general (T1, T2), we cover more, however. Namely, we naturally obtain a unifying 2-parameter family of notions of mean that includes for example the geometric, the harmonic, the arithmetic and the root-mean-square (RMS) means. And we obtain a unifying 2-parameter family of notions of entropy that, for example, includes the Rényi family of entropies.
To be precise, let us assume that a system
X has only discrete energy levels, {E
i}, where
i enumerates all the energy levels counting also possible degeneracies. Notice that {E
i} is formally what is called a multiset, because its members are allowed to occur more than once. Similarly, let us also collect the exponentiation of the negative energies
in the multiset
. Either multiset can be used to describe the same thermodynamic system X. Let
denote the inverse temperature, where
is the Boltzmann constant. The partition function of system
X,
i.e., the sum of its Boltzmann factors, then reads:
For later reference, note that the partition function is therefore related to the lp norm of X = {x1,…,xn} for through .
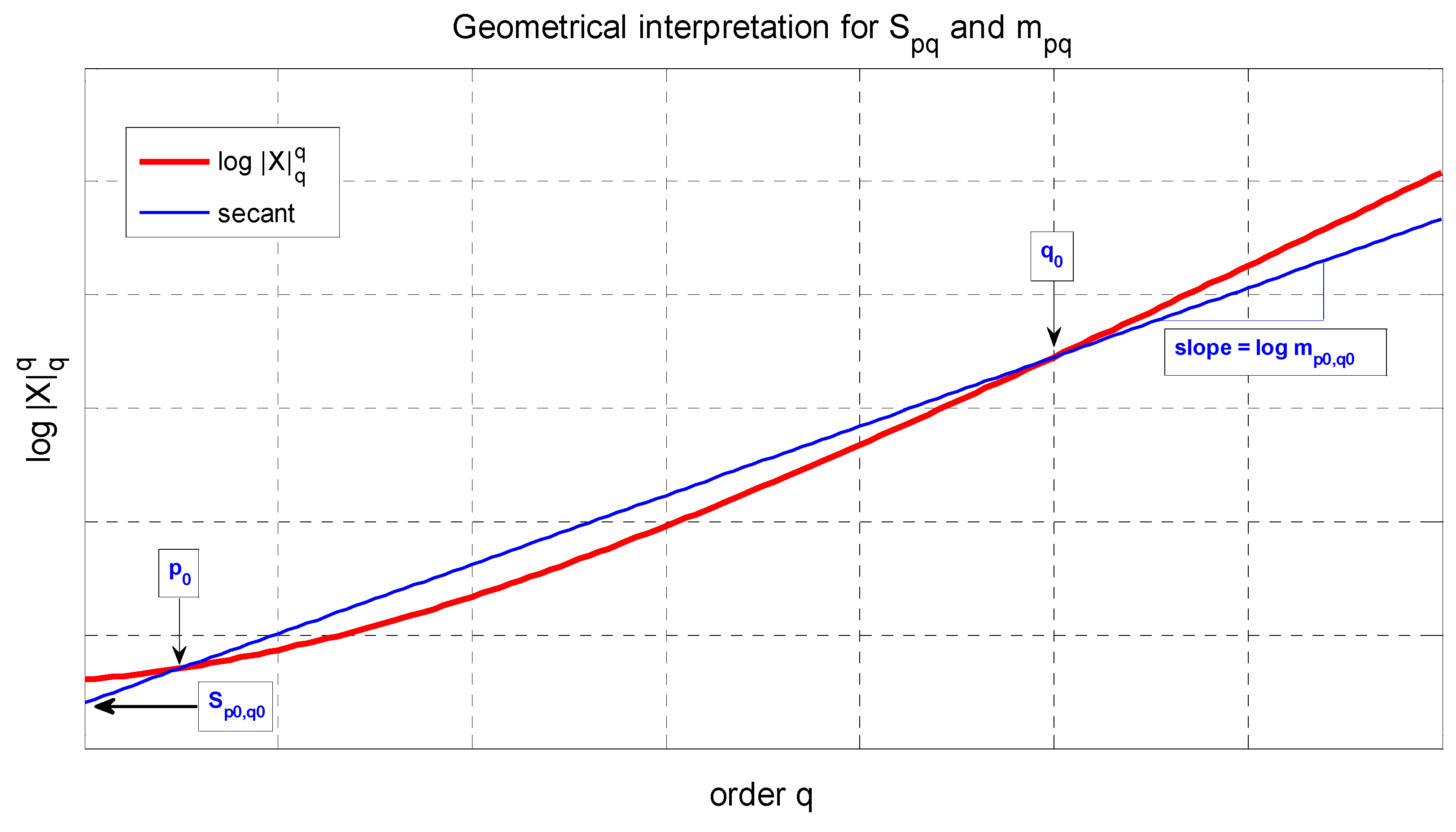
Now the key definition is that we call two physical systems -equivalent if their partition functions coincide at the two inverse temperatures , i.e., systems and are -equivalent if and . To be more explicit, one may also call such systems -partition function equivalent, or also -Helmholtz free energy equivalent, but we will here use the term -equivalent for short.
In particular, for any given system X, let us consider the -equivalent reference system M which possesses just one energy level, with energy E0 and degeneracy k, where we formally allow k to be any positive number. E0 and k are then determined by the two conditions that the partition function of M is to coincide with that of X at the two inverse temperatures and . Then, we define to be the generalized entropy, and to be the generalized mean energy of system with respect to the temperatures .
We will explore the properties of these families of generalized entropies and means in the subsequent sections. First, however, let us consider the special limiting case when the two temperatures coincide (
i.e.,
). As will be detailed in the subsequent sections of the manuscript, in this limiting case, the two equivalence conditions of partition functions can be shown to reduce to:
which can be shown to be equivalent to:
The conditions (3a) and (3b) physically mean that systems
and
have the same
partition function and
average energy, respectively, at the inverse temperature
. Notice that this is also the same as saying that the two systems have the same average
energy and the same Helmholtz free
energy at the inverse temperature
. Now by employing either pair of conditions, (2) or (3), we then recover indeed the usual thermodynamic entropy of the system
X, which is given in the Shannon form at the inverse temperature
by
The proofs of Equations (2)–(4) are straightforward. We will spell them out in detail in the subsequent sections where the setting is abstract mathematical.
Before we begin the mathematical treatment, let us remark that entropy is not only a cornerstone of thermodynamics but it is also crucial in information theory. Due to its universal significance, measures of uncertainty in the form of an entropy have been proposed by physicists and mathematicians for over a century [
2]. Our approach here for deriving a generalized family of entropies was originally motivated by basic questions regarding the effective dimensionality of multi-antenna systems (e.g., [
3,
4,
5]). After initial attempts in [
6] and later in [
5,
7], we here give for the first time a comprehensive derivation with the proofs and we also include the family of generalized means.
The manuscript is organized as follows. In
Section 2, we introduce the proposed family of entropies and means mathematically, and also show some special cases thereof. The axiomatic formulation is presented in
Section 3, followed by the study of resulting properties in
Section 4. Proofs are provided in the appendices.
2. Mathematical Definition of Generalized Entropies and Means
Let
be a multiset of real non-negative numbers, where
denotes the cardinality of
X. We assume that
X possesses at least one non-zero element. Further, let
be arbitrary fixed real numbers obeying
. Let
be a reference multiset possessing exactly one real positive element
, which is of multiplicity
. We introduce the following definitions:
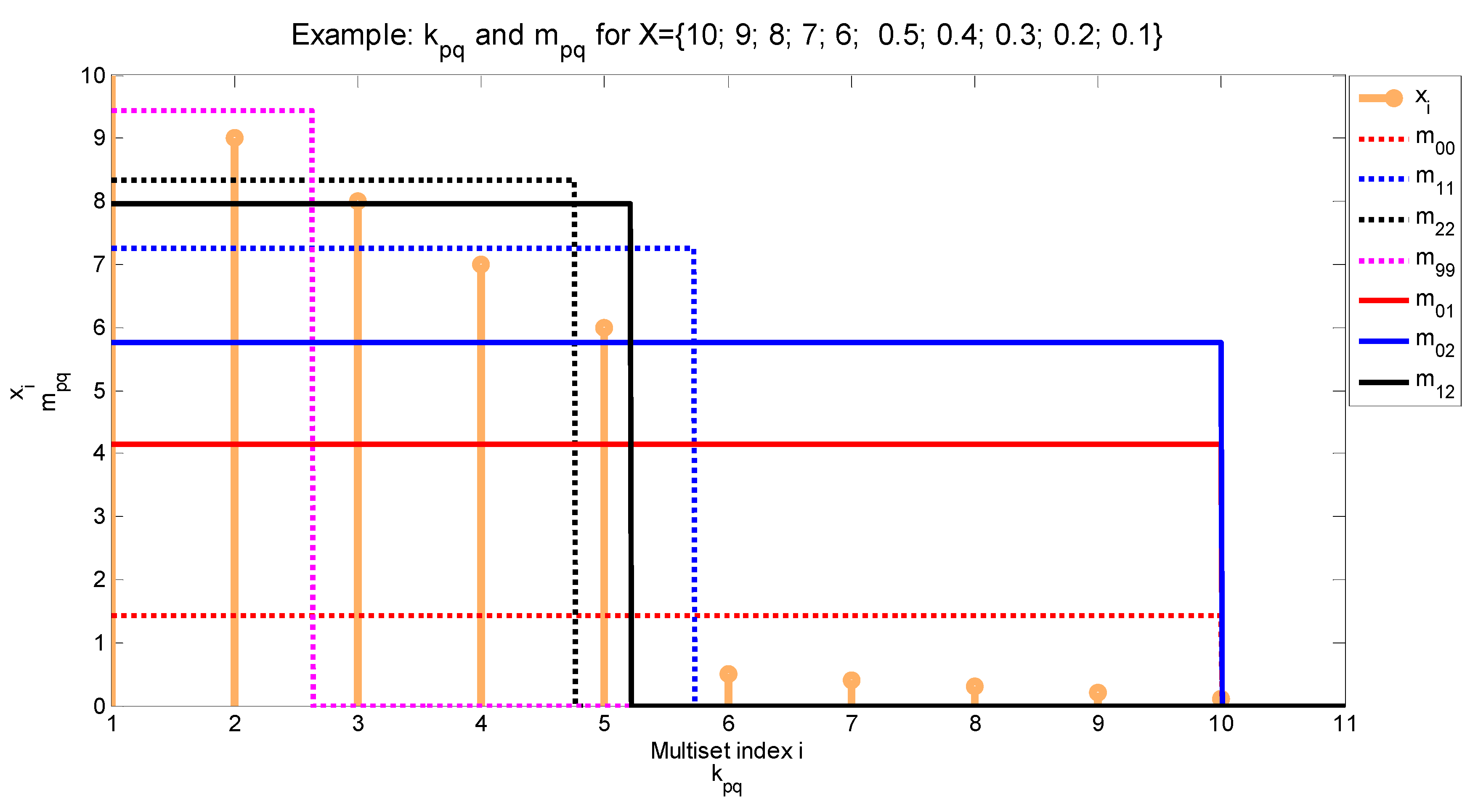
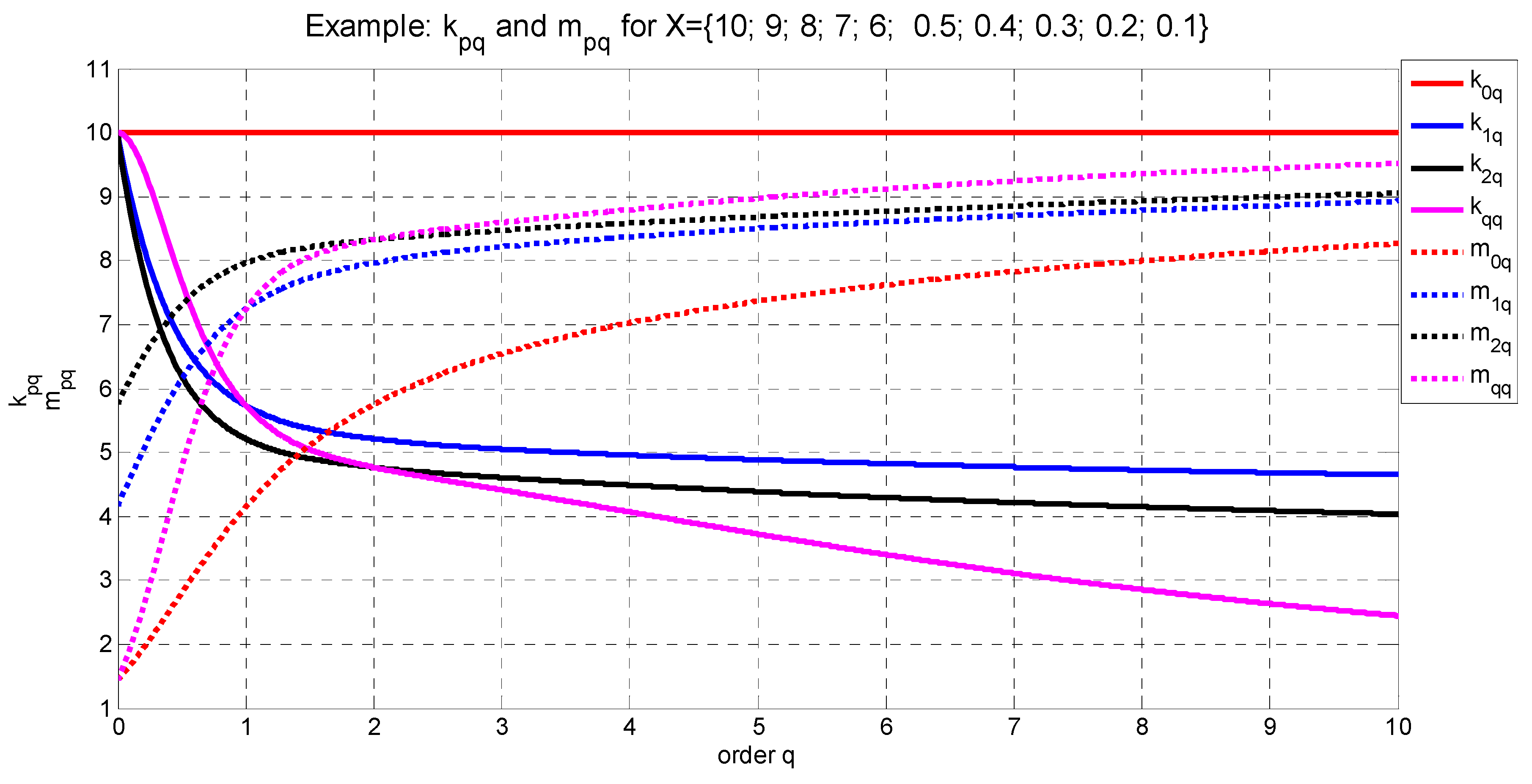
is the number of non-zero elements of X, therefore . To simplify notation, the subscript X is omitted when dealing with one multiset at hand.
is the multiplicity of the maximum elements of X
is the multiplicity of the minimum elements of X
Our objective is to determine suitable values for
and
, possibly non-integer, that can serve as mean and effective cardinality of
X, respectively, namely by imposing a suitable criterion for the equivalence of
X to a reference multiset
M. Having two unknowns (
and
) in
M, we need two equivalence conditions. We choose to impose the equivalence of the
p-norms and the
q-norms:
Here, the
p-norm
is defined as usual through:
with the proviso that
is replaced by 0 if
and
. We remark that, for
, (6) is merely a quasi-norm since the triangle inequality does not hold. Note the singularity
.
Solving for
and
in (5), we obtain:
We call
and
the norm-induced
effective cardinality and
generic mean of order
for the multiset
X, respectively. Let us now express (7) in a logarithmic form and define the entropy
as follows:
Notice that and , i.e., both the entropy and mean are symmetrical with respect to the order .
Next, we express
and
in the limiting case when
. For
we find:
where the last step is obtained by straightforward manipulations. Similarly, we find for
:
where in the second to last step, we used the fact that
, and the last step is obtained by straightforward manipulations.
It is worthwhile to mention the following useful relation linking
,
and
, which is readily deduced from (9) and (10):
We remark that in the early phase of this work [
5], each author independently suggested either
or
as two possible
distinct notions for the
effective cardinality. In [
7], it was reported that the
average energy and
Shannon entropy of a thermodynamic system are obtained by starting from equivalence of partition functions of two systems at two temperatures when the two temperatures coincide as mentioned in the introduction. Clearly, the limiting operation in (9) makes the connection and establishes (7) as the general definition of this norm-induced family of entropies and means.
In fact, for the case of degenerate order, (
), the quantities
,
, and
, could have been obtained as well through a differential equivalence of the
-norm. To see this, we impose the following two conditions:
After employing
and solving for
and
, we ultimately obtain
and
as given by (9) and (10). The condition (12) is the mathematical equivalent of the aforementioned physical condition (2) imposed on the two thermodynamic systems, which yielded the Shannon entropy form (4).
From (9), it is obvious that
is the Shannon entropy of the distribution
, which is called the escort distribution of order
[
8] of
. On the other hand,
is a more general expression of the Rényi entropy of order
. For a probability distribution
, the Rényi entropy of order
is given by [
9]:
By setting the order
in
, we obtain from (8):
By comparing (13) and (14), we readily identify
as the Rényi entropy of order
for a complete statistical distribution given by
, where the multiset elements add to 1. Formally:
In the degenerate case (when
),
is the Shannon entropy of the latter distribution. For
,
from (8) can be rearranged as a generalization of (13):
which can be viewed as the Rényi entropy of order
for the
order escort distribution
.
Rényi defined his entropy for
. We relax this condition further and allow
and
to be defined for any real indices
such that
. Accordingly, we obtain the following properties:
When at least one order
is zero, we find the interesting results:
We recognize
in (19) as the Hartley entropy [
10], which will be shown later to be the maximum value of any entropy. From (20), we obtain a famous family of generic
p-means of the non-zero elements of
X: particularly
are the minimum, harmonic mean, arithmetic mean, root-mean-square mean, and maximum, respectively. In the limiting case
, we obtain
, which is the geometric mean. In
Table 1, we summarize these and other particular cases of means and entropies at specific
. The key point is that each
uniquely defines an entropy
with a corresponding mean
, such that each pair of
and
is coupled in this sense.
Table 1.
Special cases of and . Note that and (Property 4.3).
Table 1.
Special cases of and . Note that and (Property 4.3).
| Order | | name | | name |
| | Boltzmann-Hartley entropy | | Generic mean. Specific q values are harmonic (-1), arithmetic (1), root-mean-square (2), maximum (), minimum () |
| 0,0 | | Boltzmann-Hartley entropy | | Geometric mean |
| | | | maximum |
| | | | maximum |
| | | | minimum |
| | | | minimum |
| | Rényi entropy, order , of the complete distribution | | “Rényi-like” mean |
| 1,1 | | Gibbs-Shannon entropy | | “Shannon-like” mean |
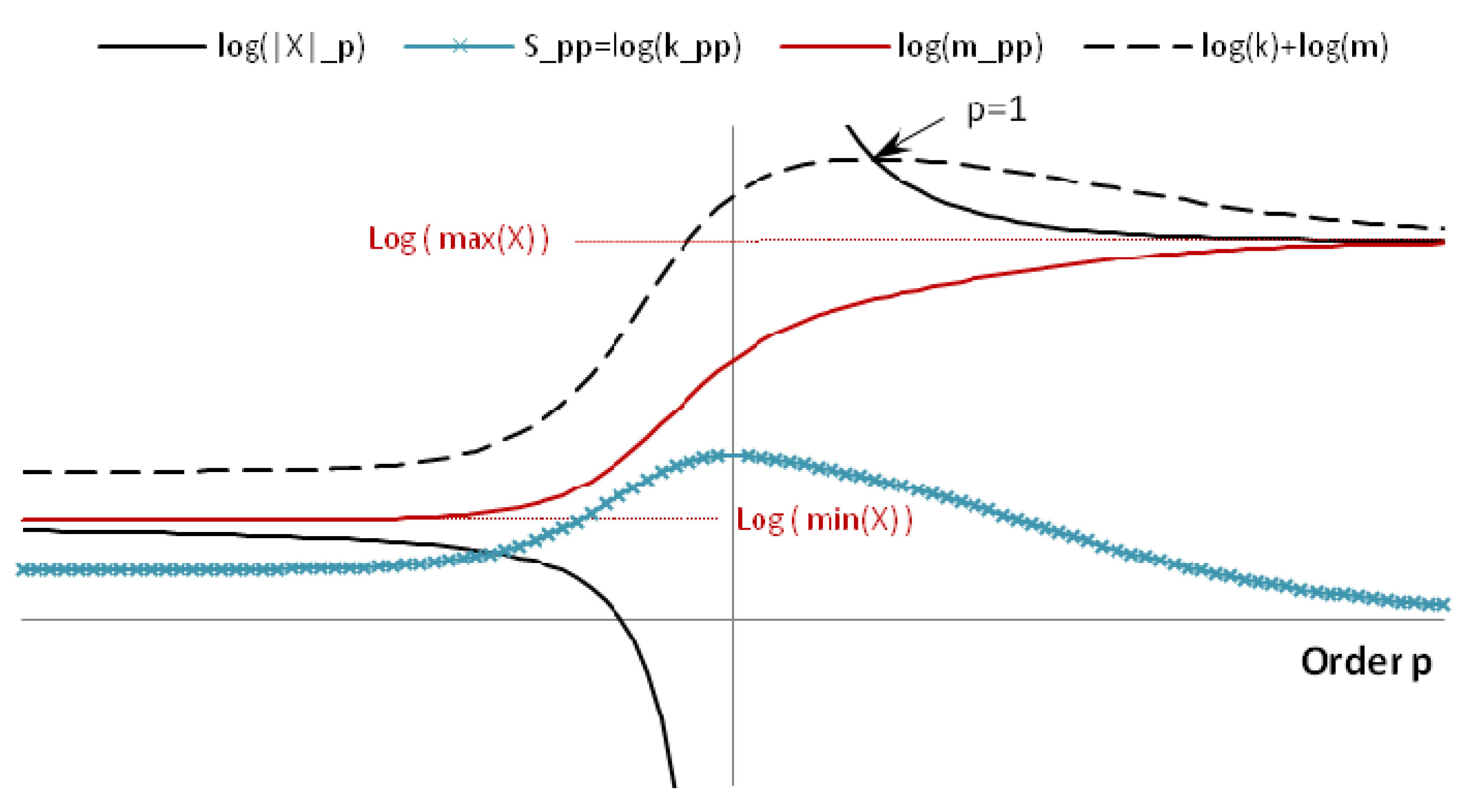
A typical plot for
,
and
is shown in log scale in
Figure 1, illustrating some of the properties to be discussed hereafter. In particular, we notice:
has a two-sided singularity at .
is non-decreasing/non-increasing for negative/positive , respectively, and is guaranteed to be maximized at . This is discussed more generally in Property 4.6.
ranges from to and is always non-decreasing with respect to . This is discussed more generally in Property 4.6.
has a specific property of making .
Figure 1.
Typical plot for , and in log scale.
Figure 1.
Typical plot for , and in log scale.
5. Discussion and Conclusions
A two-parameter family of cardinalities, entropies and means has been derived for multisets of non-negative elements. Rather than starting from thermodynamic or information theoretic considerations to derive entropies and means, see e.g., [
9,
17,
18,
19], we here defined the generalized entropies and means through simple abstract axioms. There are other families of entropies in the literature (e.g., [
23]), which are a generalization of Shannon entropy. The generalized entropy in this manuscript is shown to preserve the additivity (Property 4.8), which is not the case with the generalized entropies based on Tsallis non-additive entropy as in [
23].
Our first two axiomatizations treat the generalized entropies and means separately. It revealed that the generalized entropies are exactly those entropies that are functions of only the ratio of the multisets’ and norms. It also revealed that the generalized means are exactly those means that are functions only of the ratio of the multisets’ pth and qth moments, and . Subsequently, our unifying axiomatization characterized the generalized entropies and means together. This showed that if two multisets have exactly the same and norms, then they share the same generalized entropy and mean.
We presented several key features of the new families of generalized entropies and means, for example, that the family of generalized entropies contains and generalizes the Rényi family of entropies, of which the Shannon entropy is a special case, thus including some of the desiderata for entropies [
22]. We also showed the monotonicity with respect to
, extreme values, symmetry with respect to
, and additivity preservation. The effective cardinality
measures the distribution uniformity of the multiset elements in the sense of the
p- and
q-norm equivalence to a reference flat multiset. From an information theory perspective,
and
represent a two-parameter entropy of order
and its corresponding effective alphabet size, respectively, when a probability distribution is constructed after proper normalization of the multiset elements. Furthermore, we recall that knowing the
and
norms of a multiset is to know the multiset’s
pth and
qth moments. Our findings here therefore imply that knowledge of a multiset’s
pth and
qth moments is exactly enough information to deduce the multiset’s (
p,
q) entropy and (
p,
q) mean. Further, knowledge of sufficiently many moments of a multiset can be sufficient to reconstruct the multiset. Conversely, it should be interesting to examine how many (
p,
q)
-entropies and/or (
p,
q)
-means are required to completely determine the multiset.
Regarding the thermodynamic interpretation, we noticed that to require that the and norms of multisets coincide is mathematically equivalent to requiring that the two partition functions of two thermodynamic systems coincide at two temperatures. This in turn is equivalent to requiring that the Helmholtz free energy of the two thermodynamic systems coincide at two temperatures. The Helmholtz free energy represents the maximum mechanical work that can be extracted from a thermodynamic system under certain idealized circumstances. This suggests that there perhaps exists a thermodynamic interpretation of the generalized entropies and means in terms of the extractability of mechanical work. In this case, the fact that the generalized entropies and means depend on two rather than one temperature could be related to the fact that the maximum efficiency of a heat engine, obtained in Carnot cycles, is a function of two temperatures. We did show that in the limiting case, when the two temperatures become the same, one recovers the usual Boltzmann factor weighted mean energy as well as the usual Shannon/von Neumann entropy.