On a Connection between Information and Group Lattices
Abstract
:1. Introduction
1.1. Informationally Equivalent Random Variables
Thus we are led to define the actual information of a stochastic process as that which is common to all stochastic processes which may be obtained from the original by reversible encoding operations.
A Few Observations
1.2. Identifying Information Elements via σ-algebras and Sample-Space-Partitions
1.3. Shannon’s Legacy
andThe present note outlines a new approach to information theory which is aimed specifically at the analysis of certain communication problems in which there exist a number of sources simultaneously in operation.
It is interesting to note that current research of information inequalities are mostly motivated by network coding capacity problems.Another more general problem is that of a communication system consisting of a large number of transmitting and receiving points with some type of interconnecting network between the various points. The problem here is to formulate the best system design whereby, in some sense, the best overall use of the available facilities is made.
(The references cited above are Johnson and Suhov [8,12], Willsky [13], Maksimov [14], and Roy [15].)Despite their relatively long and roughly parallel history, surprisingly few connections appear to have been made between these two vast fields. The only attempts to do so known to the author include those of Johnson and Suhov from an information-theoretic perspective, Willsky from an estimation and controls perspective, and Maksimov and Roy from a probability perspective.
1.4. Organization
2. Information Lattices
2.1. “Being-Richer-Than” Partial Order
2.2. Information Lattices
2.3. Joint Information Element
2.4. Common Information Element
2.5. Previously Studied Lattices in Information Theory
3. Isomorphisms between Information Lattices and Subgroup Lattices
3.1. Information Lattices Generated by Information Element Sets
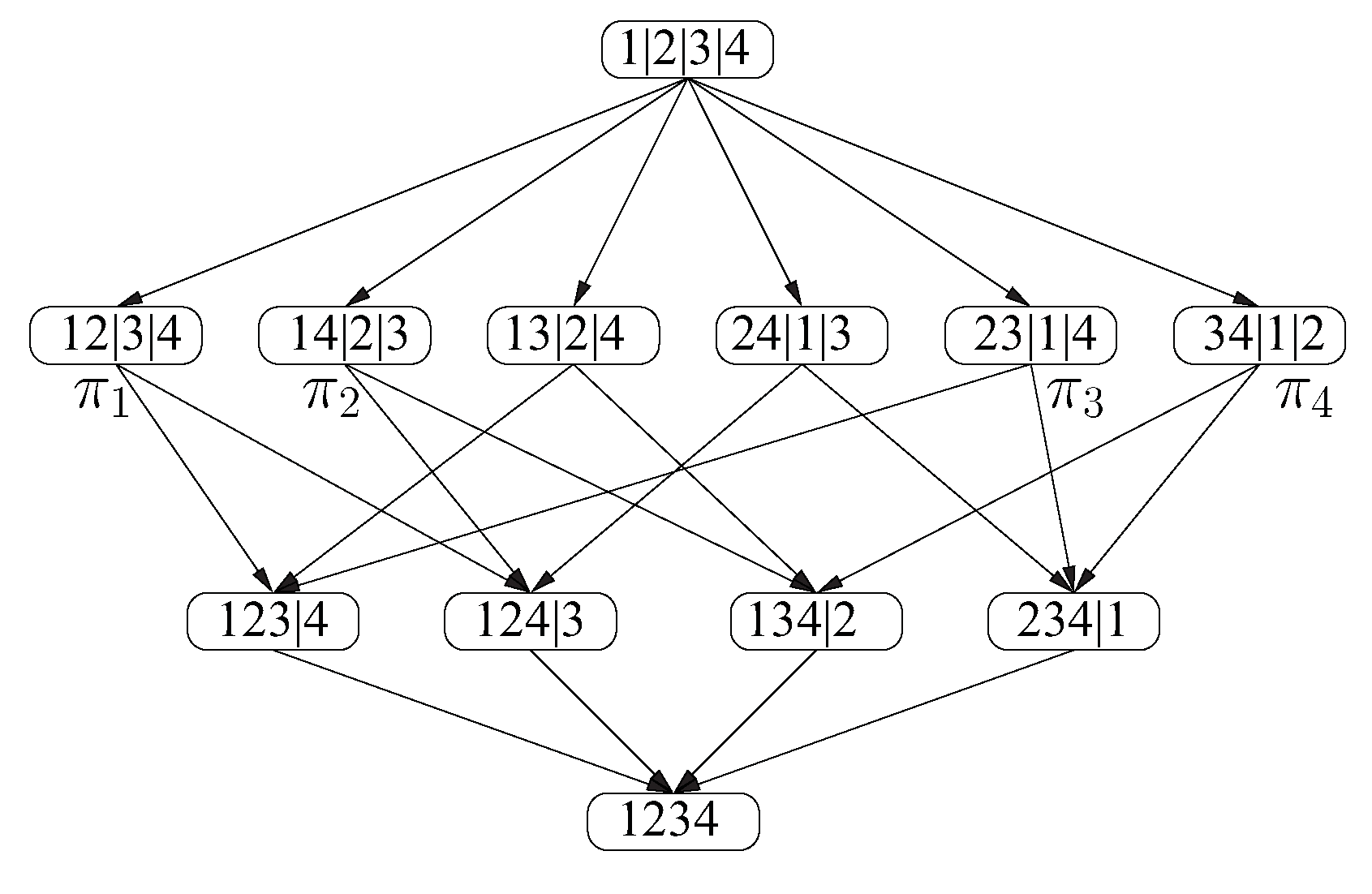
3.2. Subgroup Lattices
3.3. Special Isomorphism Theorem
3.4. General Isomorphism Theorem
3.4.1. Group-Actions and Permutation Groups
- for all and ;
- for all , where e is the identity of G.
3.4.2. Sample-Space-Partition as Orbit-Partition
3.4.3. From Coset-Partition to Orbit-Partition—From Equal Partition to General Partition
3.4.4. Isomorphism Relation Remains Between Information Lattices and Subgroup Lattices
4. An Approximation Theorem
4.1. Entropies of Coset-partition Information Elements
4.2. Subgroup Approximation Theorem
5. Parallelism between Continuous Laws of Information Elements and those of Subgroups
5.1. Laws for Information Elements
5.1.1. Non-Negativity of Entropy
5.1.2. Laws for Joint Information
5.1.3. Common Information v.s. Mutual Information
5.1.4. Laws for Common Information
5.2. Continuous Laws for Joint and Common Information
5.3. Continuous Laws for General Lattice Information Elements
5.4. Common Information Observes Neither Submodularity Nor Supermodularity Laws
6. Discussion
Acknowledgements
References
- Shannon, C.E. The lattice theory of information. IEEE Trans. Inform. Theory 1953, 1, 105–107. [Google Scholar] [CrossRef]
- Chan, T.H.; Yeung, R.W. On a relation between information inequalities and group theory. IEEE Trans. Inform. Theory 2002, 48, 1992–1995. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- Billingsley, P. Probability and Measure, 3rd ed.; Wiley-Interscience: New York, NY, USA, 1995. [Google Scholar]
- Shreve, S.E. Stochastic Calculus for Finance I: The Binomial Asset Pricing Model; Springer: New York, NY, USA, 2005. [Google Scholar]
- Ankirchner, S.; Dereich, S.; Imkeller, P. The Shannon information of filtrations and the additional logarithmic utility of insiders. Ann. Probab. 2006, 34, 743–778. [Google Scholar] [CrossRef]
- Orlitsky, A.; Santhanam, N.P.; Zhang, J. Universal compression of memoryless sources over unknown alphabets. IEEE Trans. Inform. Theory 2004, 50, 1469–1481. [Google Scholar] [CrossRef]
- Johnson, O.; Suhov, Y. Entropy and convergence on compact groups. J. Theor. Probability 2000, 13, 843–857. [Google Scholar] [CrossRef]
- Harremoës, P. Maximum entropy on compact groups. Entropy 2009, 11, 222–237. [Google Scholar] [CrossRef]
- Chirikjian, G.S. Stochastic Models, Information Theory, and Lie Groups: Volume 1 Classical Results and Geometric Methods; Birkhauser: Boston, MA, USA, 2009. [Google Scholar]
- Chirikjian, G.S. Information-Theoretic Inequalities on Unimodular Lie Groups. J. Geom. Mech. 2010, 2, 119–158. [Google Scholar] [CrossRef] [PubMed]
- Johnson, O. Information Theory and the Central Limit Theorem; Imperial College Press: London, UK, 2004. [Google Scholar]
- Willsky, A.S. Dynamical Systems Defined on Groups: Structural Properties and Estimation. Ph.D. dissertation, Dept. Aeronautics and Astronautics, MIT, Cambridge, MA, USA, 1973. [Google Scholar]
- Maksimov, V.M. Necessary and sufficient statistics for the family of shifts of probability distributions on continuous bicompact groups. Theor. Probab. Appl. 1967, 12, 267–280. [Google Scholar] [CrossRef]
- Roy, K.K. Exponential families of densities on an analytic group and sufficient statistics. Sankhy A 1975, 37, 82–92. [Google Scholar]
- Renyi, A. Foundations of Probability; Holden-Day Inc.: San Francisco, CA, USA, 1970. [Google Scholar]
- Yan, X.; Yeung, R.W.; Zhang, Z. The Capacity region for multi-source multi-sink network coding. In Proceedings of the 2007 IEEE International Symposium on Information Theory, Nice, France, 24–29 June 2007; pp. 116–120.
- Harvey, N.J.A.; Kleinberg, R.; Lehman, A.R. On the capacity of information networks. IEEE Trans. Inform. Theory 2006, 52, 2345–2364. [Google Scholar] [CrossRef]
- Pudlák, P.; Tůma, J. Every finite lattice can be embedded in a finite partition lattice. Algebra Univ. 1980, 10, 74–95. [Google Scholar] [CrossRef]
- Gács, P.; Körner, J. Common information is far less than mutual information. Probl. Control Inform. Theory 1973, 2, 149–162. [Google Scholar]
- Witsenhausen, H.S. On sequences of pairs of dependent random variables. SIAM J. Appl. Math. 1975, 28, 100–113. [Google Scholar] [CrossRef]
- Ahlswede, R.; Csiszàr, I. Common randomness in information theory and cryptography—Part I: Secret sharing. IEEE Trans. Inform. Theory 1993, 39, 1121–1132. [Google Scholar] [CrossRef]
- Ahlswede, R.; Csiszàr, I. Common randomness in information cryptography—Part II: CR capacity. IEEE Trans. Inform. Theory 1998, 44, 225–240. [Google Scholar] [CrossRef]
- Csiszàr, I.; Narayan, P. Common randomness and secret key generation with a helper. IEEE Trans. Inform. Theory 2000, 46, 344–366. [Google Scholar] [CrossRef]
- Wolf, S.; Wullschleger, J. Zero-error information and application in cryptography. In Proceedings of the 2004 IEEE Information Theory Workshop (ITW 2004), San Antonio, TX, USA, 24–29 October 2004.
- Cover, T.; Gamal, A.E.; Salehi, M. Multiple access channels with arbitrarily correlated sources. IEEE Trans. Inform. Theory 1980, 26, 648–657. [Google Scholar] [CrossRef]
- Zhang, Z. On a new non-Shannon type information inequality. Comm. Inform. Syst. 2003, 3, 47–60. [Google Scholar] [CrossRef]
- Hammer, D.; Romashchenko, A.; Shen, A.; Vereshchagin, N. Inequalities for Shannon entropy and Kolmogorov complexity. J. Comput. Syst. Sci. 2000, 60, 442–464. [Google Scholar] [CrossRef]
- Niesen, U.; Fragouli, C.; Tuninetti, D. On capacity of line networks. IEEE Trans. Inform. Theory 2011. submitted for publication. [Google Scholar] [CrossRef]
- Fujishige, S. Polymatroidal dependence structure of a set of random variables. Inform. Contr. 1978, 39, 55–72. [Google Scholar] [CrossRef]
- Cicalese, F.; Vaccaro, U. Supermodularity and subadditivity properties of entropy on the majorization lattice. IEEE Trans. Inform. Theory 2002, 48, 933–938. [Google Scholar] [CrossRef]
- Chernov, A.; Muchnik, A.; Romashchenko, A.; Shen, A.; Vereshchagin, N. Upper semilattice of binary strings with the relation `x is simple conditional to y’. Theor. Comput. Sci. 2002, 271, 69–95. [Google Scholar] [CrossRef]
- Dummit, D.S.; Foote, R.M. Abstract Algebra, 3rd ed.; Wiley: New York, NY, USA, 2003. [Google Scholar]
- Yeung, R.W. A First Course in Information Theory; Kluwer Academic/Plenum Publishers: New York, NY, USA, 2002. [Google Scholar]
- Oxley, J.G. Matroid Theory; Oxford University Press: New York, NY, USA, 1992. [Google Scholar]
- Zhang, Z.; Yeung, R.W. On characterization of entropy function via information inequalities. IEEE Trans. Inform. Theory 1998, 44, 1440–1452. [Google Scholar] [CrossRef]
- Dougherty, R.; Freiling, C.; Zeger, K. Six New Non-Shannon information inequalities. In Proceedings of the 2006 IEEE International Symposium on Information Theory, Seattle, WA, USA, 9–14 July 2006; pp. 233–236.
- Pippenger, N. What are the laws of information theory. In Proceedings of the 1986 Special Problems on Communication and Computation Conference, Palo Alto, CA, USA, 3–5 September 1986.
- Matúš, F. Piecewise linear conditional information inequality. IEEE Trans. Inform. Theory 2006, 52, 236–238. [Google Scholar] [CrossRef]
- Li, H.; Chong, E.K.P. On connections between group homomorphisms and the Ingleton inequality. In Proceedings of the 2007 IEEE International Symposium on Information Theory, Nice, France, 24–29 June 2007; pp. 1996–2000.
- Chan, T. Recent progresses in characterising information inequalities. Entropy 2011, 13, 379–401. [Google Scholar] [CrossRef]
- Chan, T. On the optimality of group network codes. In Proceedings of the International Symposium on Information Theory, Adelaide, Australia, 4–9 September 2005.
- Mao, W.; Thill, M.; Hassibi, B. On group network codes: Ingleton-bound violations and independent sources. In Proceedings of the 2010 IEEE International Symposium on Information Theory, Austin, TX, USA, 13–18 June 2010; pp. 2388–2392.
- Matúš, F. Infinitely many information inequalities. In Proceedings of the 2007 IEEE International Symposium on Information Theory, Nice, France, 24–29 June 2007; pp. 41–44.
Appendix
A. Proof of Theorem 1
- , for all and ;
- For any , if and , thenand
B. Proof of Theorem 3
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an Open Access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/.)
Share and Cite
Li, H.; Chong, E.K.P. On a Connection between Information and Group Lattices. Entropy 2011, 13, 683-708. https://doi.org/10.3390/e13030683
Li H, Chong EKP. On a Connection between Information and Group Lattices. Entropy. 2011; 13(3):683-708. https://doi.org/10.3390/e13030683
Chicago/Turabian StyleLi, Hua, and Edwin K. P. Chong. 2011. "On a Connection between Information and Group Lattices" Entropy 13, no. 3: 683-708. https://doi.org/10.3390/e13030683
APA StyleLi, H., & Chong, E. K. P. (2011). On a Connection between Information and Group Lattices. Entropy, 13(3), 683-708. https://doi.org/10.3390/e13030683



