1. Introduction
Low dimensional strange attractors—those with Lyapunov dimension
—can be discretely classified. A doubly discrete classification has been described in [
1]. This classification depends ultimately on the existence and rigid organization of an infinity of unstable periodic orbits in a strange attractor [
2,
3]. At the lowest level this classification depends on a basis set of orbits. This is a set of orbits with positive topological entropy whose presence forces the existence of all the other unstable periodic orbits in the attractor [
4,
5,
6]. The basis set of orbits for any attractor is discrete, and up to any finite period the basis set of orbits is finite.
At the second level of this organizational hierarchy for strange attractors are branched manifolds [
1,
2,
7,
8,
9]. These are obtained from the flow that generates a strange attractor by projecting the flow down along the stable direction. The unstable periodic orbits that exist in the strange attractor exist in 1-1 correspondence with the periodic orbits on the branched manifold, with possibly a small number of exceptions. Information about branched manifolds can be extracted from experimental data [
10].
Recently a third level of discreteness in the description and classification of low dimensional strange attractors has been introduced [
11,
12]. Branched manifolds can be enclosed in bounding tori. These serve to organize branched manifolds in the same way that branched manifolds organize the periodic orbits in a strange attractor. A bounding torus provides a canonical form for any flow in
that generates a strange attractor. An algorithm for transforming a flow to its canonical form is given in [
12]. The bounding tori that enclose every strange attractor that has been studied in
have been described in [
11,
12].
Bounding tori are described first by their genus,
. However, genus alone does not uniquely identify a bounding torus when
, and in fact the number of distinct bounding tori of genus
g,
, grows rapidly with
g. Each distinct bounding torus describes a different class of tearing and squeezing processes (or mechanisms) that serve to create strange attractors. The number of distinct mechanisms responsible for generating chaotic behavior grows with
. It was proposed in [
12] that the growth might be exponential, so that an entropy-like limit of the type
might exist, in analogy with the limiting definition of topological entropy to describe the growth in the number of periodic orbits of period
p with the period,
p, in a strange attractor. The term entropy is being used here to quantify the complexity of an entire class of dynamical systems,
i.e., to describe the growth rate in the number of topologically distinct dynamical systems for a given genus. This is in contrast to the typical use of entropy in dynamical systems theory, which quantifies the complexity in the orbit structure of a single dynamical system.
The purpose of the present work is to show that this limit exists and to evaluate it. We show that
so that an entropy of log(3) can be associated with the growth in the number of bounding tori with genus
g in
.
2. Background
A bounding torus of genus
is shown in
Figure 1. This represents a projection of a two dimensional surface without self-links in
down onto a plane. The projection can always be brought to a canonical form [
11,
12]. In that form the projection consists of the outer boundary of a disk and
g interior disks. The interior disks are of two types:
circles and
even-sided polygons, where
. The flow on the outer boundary is unidirectional; the flow on the
interior circles is also unidirectional, and in the same direction as the flow on the exterior boundary. All singularities of the flow lie on the
interior polygons: a polygon with
sides (
) has
singularities, one at each vertex. Half the singularities on a polygon are tearing singularities; the other half are joining singularities. The total number of singularities on the bounding torus (all at the vertices of the interior polygons) is
[
11,
12].
For the bounding torus shown in
Figure 1 there are
interior uniflow circles labeled
and three interior polygons labeled
. The global Poincaré section of any flow bounded by this torus has
disconnected components [
11,
12]. These are shown as line segments in
Figure 1 and labeled
, sequentially in the direction of the flow along the exterior boundary. At the tearing singularity at the top of the square labeled
b, the flow from component 2 of the Poincaré section is directed to either component 3 or component 4 of the Poincaré section. Similarly, the flow to component 4 of the Poincaré section from components 2 and 3 meet at the joining singularity on the right side of
b. A bounding torus of genus
g describes how the
tearing singularities and the
joining singularities are arranged in phase space with respect to each other to define a mechanism for creating chaotic behavior. The number of tearing and squeezing mechanisms therefore grows with genus as
.
There are several ways that bounding tori can be uniquely identified. The labeling algorithms are described in Equation
2.
Figure 1.
A canonical bounding torus with genus 8. This is partly described by Young partition (3,2,2).
Figure 1.
A canonical bounding torus with genus 8. This is partly described by Young partition (3,2,2).
The first row lists the components of the global Poincaré section in the order they are encountered traversing the exterior boundary of the projection in the direction of the flow. Below each integer
i (
) is the capital letter (
) that identifies the uniflow circle to which the
component of the surface of section is attached. The sequence (
) that is encountered is shown in the second row of Equation
2. In moving from component
i to component
a hole with singularities is encountered. The sequence (
) that is encountered is shown in the third row of Equation
2. There is a 1-1 correspondence between the bounding torus and each of the two letter sequences (
and
), up to the usual symmetries (relabeling the holes, changing the starting point). In fact, these two descriptions of a bounding torus are dual to each other. Both sequence strings are in fact infinite, but of finite period
. The last string of integers in Equation
2 indicates that there is an orbit of topological period 3 around hole
B and period-1 orbits around the holes
. A permutation group representation of this bounding torus in terms of permutation group generating cycles is (2,4,6)(1)(3)(5)(7) or more simply (2,4,6). This representation in terms of generating cycles can be used algorithmically to construct the transition matrix for this bounding torus [
11,
12].
Part of the degeneracy associated with enumerating bounding tori of genus
g can be lifted by introducing Young partitions
,
[
11,
12]. Each internal polygon with
edges and singularities is visited exactly
times in a tour around the exterior boundary. The partition associated with the torus has
rows, one for each interior polygon. For the bounding torus shown in
Figure 1,
because hole
a is encountered three times and holes
b and
c twice each on a round trip round the exterior boundary. All allowed bounding tori that can be associated with this partition are obtained by distributing the
letters
,
, and
on the perimeter of a circle subject to the single condition that no interleaving occurs (
is allowed but
is not). “Interleaving” is an algebraic representation of the geometric idea that the holes must be encountered in a precisely defined way. A geometric test for interleaving is as follows. Cyclically permute the word until all letters of any one type occur at the beginning of a word (
). Delete these letters (
). Continue cyclic rotation and deletion until it is no longer possible. If nothing remains, no interleaving is present and the original word represents an allowed bounding torus. If something nonzero remains there is interleaving in the original word, which does not represent an allowed bounding torus.
The number of bounding tori of genus g can be determined by
The sequence of polygon encounters can be replaced by a sequence of three symbols: (, ), and ∗. The opening and closing parentheses stand for the first and last occurrence, respectively, of a given letter, intermediate occurrences being indicated by a ∗. The non-interleaving property implies that each ∗ belongs to the innermost pair of parentheses between which it is embedded. Thus , , , and . This construction guarantees that at each position of the sequence the cumulative number of opening parentheses is not less than the cumulative number of closing parentheses, counting from the left.
The complete set of bounding tori of genus g is obtained by constructing all three-symbol sequences that satisfy the requirements (a) that the total number of opening parentheses be equal to that of closing parentheses, (b) that the cumulative number of opening parentheses be always not less than that of closing parentheses, (c) that a ∗ can only appear if the number of opening parentheses preceding it is larger than the number of closing parentheses. Finally, (d) sequences that are related by a cyclic permutation are equivalent. Cyclic permutations are more easily described in terms of letter sequences than three-symbol sequences. Thus translates to .
Requirements (a)–(c) are in 1-1 correspondence with the properties satisfied by the coupled states of spin-1 particles. This is established by observing that coupling spins with total spin to a single spin is isomorphic with the three-symbol coupling problem under the association: ( increases the spin []; ∗ preserves the spin []; and ) decreases the spin [], subject to the condition that . Requirement (a) corresponds to the specific case .
This algorithm for describing the complete set of bounding tori of genus-
g is described more fully in
Section 4.
4. Lower Bound and Exact Results
The algorithm for building (and counting) the complete set of inequivalent three-symbol sequences of length that respect requirements (a)-(d) proceeds as follows: An overcomplete list is generated from the complete set of sequences of length by applying to each one of them the following operations: (1) Inserting a ∗ at each legal position (i.e., lengthening a cycle). (2) Replacing a ∗ by the sequence (i.e., embedding a two-cycle). (3) Replacing a ∗ by the sequence (i.e., splitting a cycle into two cycles). In fact, operation (3) is only capable of generating sequences that have not already been generated by operations (1) and (2) if applied to a length sequence with a maximum () number of cycles.
The list thus created contains repetitions that have to be eliminated. Furthermore, sequences on the list that are equivalent by cyclic permutations to other sequences need to be discarded. This algorithm was implemented by Maple and Fortran codes and used to compute
for
g up to 20. These results are reported in
Table 1. Values for
were computed by hand up to
to validate the algorithm and the coding of it.
In the case that
is prime a simple closed-form expression for
can be constructed. It is deduced from the expression for the number of different ways that a total spin
can be computed from
p spins
. The number of ways that
n spins
can be combined to a total spin
is
The number
includes spin coupling patterns that correspond to letter sequences that are related by cyclic permutations. These must be removed to relate the spin coupling problem to the bounding torus problem, that is, to satisfy requirement (d) of
Section 2. One of the sequences (
) is already cyclically invariant and all the others have periodicity
. The relation between
and
for
prime is
When
is not a prime some of the spin coupling patterns correspond to periodicity lower than
, so that the above expression for
is actually a lower bound for nonprime cases. The extension of Equation
4 to the case
nonprime requires the determination of the number of ways of forming distinct sequences with the various periodicities that correspond to the factors of
. For example, the cyclic permutations of
are all distinct while those of
(
) are not. The simpler problem involving just the two symbols ( and ) [or coupling of spin
particles] has been solved, and involves complicated number-theoretic functions such as the Euler totient function [
13]. Equation
4 was used to compute
for odd
. Results are presented in
Table 2. This table shows that the values computed for prime values of
are equal to those computed by hand (
) and by the Fortran algorithm, while the values of
for
not prime (9, 15) are slightly below the exact values by a relative fraction that decreases as
g increases. Only odd integers are included in this table to provide a reasonable mixture of prime and nonprime integers: all even integers greater than 2 are nonprime.
Table 1.
Number of canonical bounding tori as a function of genus, g.
Table 1.
Number of canonical bounding tori as a function of genus, g.
| g | | | g | | | g | |
| 3 | 1 | | 9 | 15 | | 15 | 2211 |
| 4 | 1 | | 10 | 28 | | 16 | 5549 |
| 5 | 2 | | 11 | 67 | | 17 | 14290 |
| 6 | 2 | | 12 | 145 | | 18 | 36824 |
| 7 | 5 | | 13 | 368 | | 19 | 96347 |
| 8 | 6 | | 14 | 870 | | 20 | 252927 |
Table 2.
Comparison of exact results for with analytic result for prime numbers.
Table 2.
Comparison of exact results for with analytic result for prime numbers.
| Exact | From (4) | |
| 3 | 1 | 1 | |
| 5 | 2 | 2 | |
| 7 | 6 | 6 | |
| 9 | 28 | 26 | |
| 11 | 145 | 145 | |
| 13 | 870 | 870 | |
| 15 | 5549 | 5540 | |
| 17 | 36824 | 36824 | |
| 19 | 252927 | 252927 | |
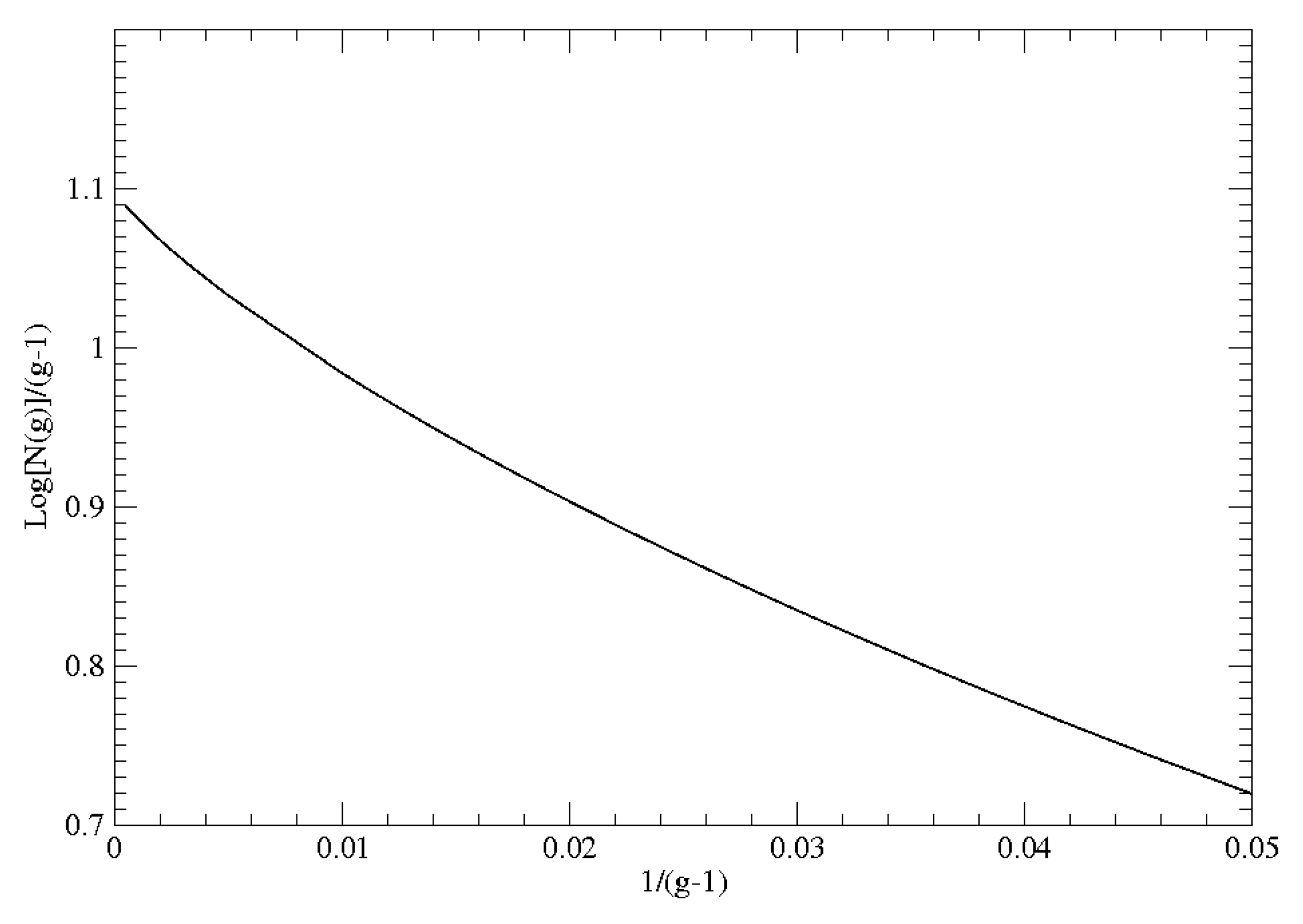
We have computed
for prime values of
and plotted this ratio as a function of
for primes below 2,000. The results are presented in
Figure 2. The lower bound can be computed analytically in the limit
using Stirling’s approximation and is equal to log(3). Since the upper bound is also
, the entropy of bounding tori is
.
Figure 2.
The ratio converges to log(3).
Figure 2.
The ratio converges to log(3).