1. Introduction
Estimating differential entropy and relative entropy is useful in many applications of coding, machine learning, signal processing, communications, chemistry, and physics. For example, relative entropy between maximum likelihood-fit Gaussians has been used for biometric identification [
1], differential entropy estimates have been used for analyzing sensor locations [
2], and mutual information estimates have been used in the study of EEG signals [
3].
In this paper we present Bayesian estimates for differential entropy and relative entropy that are optimal in the sense of minimizing expected Bregman divergence between the estimate and the uncertain true distribution. We illustrate techniques that may be used for a wide range of parametric distributions, specifically deriving estimates for the uniform (a non-exponential example), Gaussian (perhaps the most popular distribution), and the Wishart and inverse Wishart (the most commonly used distributions for positive definite matrices).
Bayesian estimates for differential entropy and relative entropy have previously been derived for the Gaussian [
4], but our estimates differ in that we take a distribution-based approach, and we use a prior that results in numerically stable estimates even when the number of samples is smaller than the dimension of the data. Performance of the presented estimates will depend on how well the user is able to choose the prior distribution’s parameters, and we do not attempt a rigorous experimental study here. However, we do present simulated results for the uniform distribution (where no prior is needed), that show that our approach to forming these estimates can result in significant performance improvements over maximum likelihood estimates and over the state-of-the-art nearest-neighbor nonparametric estimates [
5].
First we define notation that will be used throughout the paper. In Section II we review related work in estimating differential entropy and relative entropy. In Section III we show that the proposed Bayesian estimates are optimal in the sense of minimizing expected Bregman divergence loss. In the remaining sections, we present differential entropy and relative entropy estimates for the uniform, Gaussian, Wishart and inverse Wishart distributions given iid samples drawn from the underlying distributions.
All proofs and derivations are in the
Appendix.
1.1. Notation and Background
If
P and
Q were the known parametric distributions of two random variables with respective densities
p and
q, then the differential entropy of
P is
and the relative entropy between
P and
Q is
For estimating differential entropy, we assume that one has drawn iid samples from distribution P where is a vector, and the samples have mean and scaled sample covariance . The notation will be used to refer to the value of the ith component of vector .
For estimating relative entropy, we assume that one has drawn iid d-dimensional samples from both distributions P and Q, and we denote the samples drawn from P as and the samples drawn from Q as . The empirical means are denoted by and , and the scaled sample covariances are denoted by and .
In some places, we treat variables such as the covariance Σ as random, and we consistently denote realizations of random variables with a tilde, e.g., . Expectations are always taken with respect to the posterior distribution unless otherwise noted. The digamma function is denoted by , where Γ is the standard gamma function; and denotes the standard multi-dimensional gamma function.
Let
W be distributed according to a Wishart distribution with scalar degree of freedom parameter
and positive definite matrix parameter
if
Let
V be distributed according to an inverse Wishart distribution with scalar degree of freedom parameter
and positive definite matrix parameter
if
Note that
is then distributed as a Wishart random matrix with parameters
q and
.
2. Related Work
First we review related work in parametric differential entropy estimation, then in nonparametric differential entropy estimation, and then in estimating relative entropy.
2.1. Prior Work on Parametric Differential Entropy Estimation
A common approach to estimate differential entropy (and relative entropy) is to find the maximum likelihood estimate for the parameters and then substitute them into the differential entropy formula. For example, for the multivariate Gaussian distribution, the maximum likelihood differential entropy estimate of a
d-dimensional random vector
X drawn from the Gaussian
is
Similarly, if samples
are drawn iid from a one-dimensional uniform distribution, the maximum likelihood differential entropy estimate is
, which will always be an under-estimate of the true differential entropy.
Ahmed and Gokhale investigated uniformly minimum variance unbiased (UMVU) differential entropy estimators for parametric distributions [
6]. They stated that the UMVU differential entropy estimate for the Gaussian is:
However, they treated the random sample covariance of
n IID Gaussian samples as if it were drawn from a Wishart with
n degrees of freedom, when in fact it is drawn from a Wishart of
degrees of freedom, and thus the UMVU estimator they derived should be stated:
Bayesian differential entropy estimation was first proposed for the multivariate normal in 2005 by Misra
et al. [
4]. They formed an estimate of the multivariate normal differential entropy by substituting
for
in the differential entropy formula for the Gaussian, where their
minimizes the expected squared-difference of the differential entropy estimate:
They also considered different priors with support over the set of positive definite matrices. Using the prior
to solve (
5) results in the same estimate as the correct UMVU estimate [
4], given in (
4). Misra
et al. show that (
4) is dominated by a Stein-type estimator
, where
is a function of
d and
n [
4]. In addition, they show that (
4) is dominated by a Brewster-Zidek-type estimator
, where
is a function of
and
that requires calculating the ratio of two definite integrals, stated in full in (4.3) of [
4]. Misra
et al. found that on simulated numerical experiments their Stein-type and Brewster-Zidek-type estimators achieved roughly only
improvement over (
4), and thus they recommend using the computationally much simpler (
4) for applications.
There are two practical problems with the previously proposed parametric differential entropy estimators. First, the estimates given by (
3), (
4), and the other estimators investigated by Misra
et al. require calculating the determinant of
S or
, which is problematic if
. Second, the estimate (
4) uses the digamma function of
which requires
samples so that the digamma has a non-negative argument. Thus, although the knowledge that one is estimating the differential entropy of a Gaussian should be of use, for the
case one must currently turn to nonparametric differential entropy estimators.
2.2. Prior Work on Nonparametric Differential Entropy Estimation
Nonparametric differential entropy estimation up to 1997 has been thoroughly reviewed by Beirlant
et al. [
7], including density estimation approaches, sample-spacing approaches, and nearest-neighbor estimators. Recently, Nilsson and Kleijn show that high-rate quantization approximations of Zador and Gray can be used to estimate Renyi entropy, and that the limiting case of Shannon entropy produces a nearest-neighbor estimate that depends on the number of quantization cells [
8]. The special case that best validates the high-rate quantization assumptions is when the number of quantization cells is as large as possible, and they show that this special case produces the nearest-neighbor differential entropy estimator originally proposed by Kozachenko and Leonenko in 1987 [
9]:
where
γ is the Euler-Mascheroni constant, and
is the volume of the
d-dimensional hypersphere with radius 1:
. Other variants of nearest-neighbor differential entropy estimators have also been proposed and analyzed [
10,
11]. A practical problem with the nearest-neighbor approach is that data samples are often quantized, for example, image pixel data are usually quantized to eight bits or ten bits. Thus, it can happen in practice that two samples
and
have the exact same measured value so that
and the differential entropy estimate is ill-defined. Though there are various fixes, such as pre-dithering the quantized data, it is not clear what effect such fixes could have on the estimated differential entropy.
A different approach is taken by Hero
et al. [
12,
13,
14]. They relate a result of Beardwood-Halton-Hammersley on the limiting length of a minimum spanning graph to Renyi entropy, and form a Renyi entropy estimator based on the empirical length of a minimum spanning tree of data. Unfortunately, how to use this approach to estimate the special case of Shannon entropy remains an open question.
In other recent work on differential entropy estimation, Van Hulle took a semiparametric approach to nonparametric differential entropy estimation for a continuous density by using a 5th-order Edgeworth expansion about the maximum likelihood multivariate normal given the data samples drawn from a non-normal distribution [
15].
2.3. Prior Work on Relative Entropy Estimation
There is relatively little work on estimating relative entropy for continuous distributions. Wang
et al. explored a number of data-dependent partitioning approaches for relative entropy between any two absolutely continuous distributions [
16]. Nguyen
et al. took a variational approach to relative entropy estimation [
17], which was reported to work better for some cases than the data-partitioning estimators.
In more recent work [
5,
18], Wang
et al. proposed a nearest-neighbor estimator based on nearest-neighbor density estimation:
where
They showed that (
7) significantly outperforms their best data-partitioning estimators [
5,
18]. Peréz-Cruz has contributed additional convergence analysis for these estimators [
19]. In practice, like the nearest-neighbor entropy estimate,
may be ill-defined if samples are quantized.
The nearest-neighbor relative entropy estimator can perform quite poorly for Gaussian distributed data given a reasonable number of finite samples, particularly in high-dimensions. For example, consider the case of two high-dimensional Gaussians each with identity covariance and a finite iid sample of points from the two distributions. Their true relative entropy is a function of , whereas the nearest neighbor estimated relative entropy is better approximated (though roughly so) as a function of .
3. Functional Estimates that Minimize Expected Bregman Loss
Here we propose to form estimators of functionals (such as differential entropy and relative entropy) that are optimal in the sense that they minimize the expected Bregman loss, and that are always computable (assuming an appropriate prior is used).
Consider samples drawn iid from some unknown distribution A, where we model A as a random distribution drawn from a distribution over distributions that has density . We use to denote a realization of the random distribution A.
The goal is to estimate some functional (such as differential entropy or relative entropy) ξ, where ξ maps a distribution or set of distributions (e.g., relative entropy is a functional on pairs of distributions) to a real number , where is the Cartesian product of finite distributions , and we denote a realization of as . For example, the functional relative entropy maps a pair of distributions to a non-negative number.
We are interested in the Bayesian estimate of
ξ that minimizes an expected loss
[
20]:
In this paper, we will focus on Bregman loss functions (Bregman divergences), which include squared error and relative entropy [
21,
22,
23,
24]. For any twice differentiable strictly convex function
, the corresponding Bregman divergence is
for
.
The following proposition will aid in solving (8):
Proposition 1. The expected functional minimizes the expected Bregman loss such thatif exists and is finite. One can view this proposition as a special case of Theorem 1 of Banerjee
et al. [
22]; we provide a proof in the
appendix for completeness.
In this paper we focus on estimating differential entropy and relative entropy, which by applying Proposition 1 we calculate respectively as:
assuming the expectations are finite.
4. Bayesian Differential Entropy Estimate of the Uniform Distribution
We present estimates of the differential entropy of an unknown uniform distribution over a hyperrectangular domain for two cases: first, that there is no prior knowledge about the uniform distribution; and second, that there is prior knowledge about the uniform given in the form of a Pareto prior.
4.1. No Prior Knowledge About the Uniform
Given
n d-dimensional samples
drawn from a hyperrectangular
d-dimensional uniform distribution, let
be the difference between the maximum and minimum sample in the
ith dimension:
Then because a hyperrectangular uniform is the product of independent marginal uniforms, its differential entropy is the sum of the marginal entropies. Given no prior knowledge about the uniform, we take the expectation with respect to the (normalized) likelihood, or equivalently using a non-informative flat prior. Then, the proposed differential entropy estimate is the sum over dimensions of the differential entropy estimate for each marginal uniform:
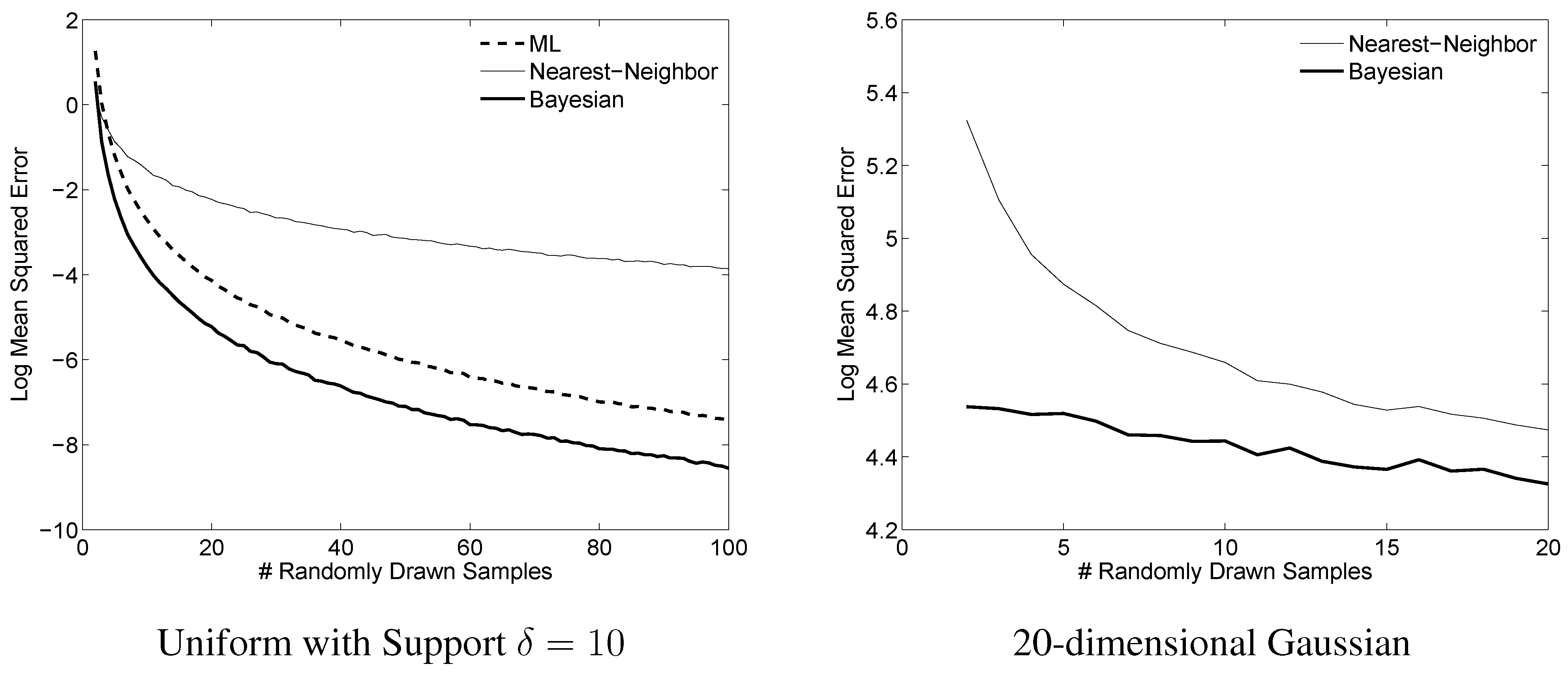
To illustrate the effectiveness of the proposed Bayesian estimates, we show example results from two representative experiments in
Figure 1.
Figure 1.
Example comparison of differential entropy estimators. Left: For each of 10,000 runs of the simulation,
n samples were drawn iid from a uniform distribution on
. The proposed estimate (9) is compared to the maximum likelihood estimate, and to the nearest-neighbor estimate given in (
6). Right: For each of 10,000 runs of the simulation,
n samples were drawn iid from a Gaussian distribution. For each of the 10,000 runs, a new Gaussian distribution with diagonal covariance was randomly generated by drawing each of the variances iid from a uniform on
. The Bayesian estimator prior parameters were
and
. The proposed estimate (12) is compared to the only feasible estimator for this range of
n, the nearest-neighbor estimate given in (
6).
Figure 1.
Example comparison of differential entropy estimators. Left: For each of 10,000 runs of the simulation,
n samples were drawn iid from a uniform distribution on
. The proposed estimate (9) is compared to the maximum likelihood estimate, and to the nearest-neighbor estimate given in (
6). Right: For each of 10,000 runs of the simulation,
n samples were drawn iid from a Gaussian distribution. For each of the 10,000 runs, a new Gaussian distribution with diagonal covariance was randomly generated by drawing each of the variances iid from a uniform on
. The Bayesian estimator prior parameters were
and
. The proposed estimate (12) is compared to the only feasible estimator for this range of
n, the nearest-neighbor estimate given in (
6).
4.2. Pareto Prior Knowledge About the Uniform
We consider the case that one has prior knowledge about the random uniform distribution
U, where that prior knowledge is formulated as an independent Pareto prior for each dimension such that the prior probability of the marginal
ith-dimension uniform
with support of length
δ is:
where
and
are the Pareto distribution prior parameters for the
ith dimension. The parameter
defines the minimum length one believes the uniform’s support could be in the
ith dimension, and the parameter
specifies the confidence that
is the right length; a larger
means one is more confident that
is the correct length.
Then the differential entropy estimate for the
ith dimension’s one-dimensional uniform is:
Note that the two cases given above do coincide for the boundary case that
, so that this differential entropy estimate is a continuous function of
. For the full
d-dimensional uniform, the differential entropy estimate is the sum of the one-dimensional differential entropy estimates:
.
5. Gaussian Distribution
The Gaussian is a popular model and often justified by central limit theorem arguments and because it is the maximum entropy distribution given fixed mean and covariance. In this section we assume d-dimensional samples have been drawn iid from an unknown Gaussian N, which we model as a random Gaussian and we take the prior to be an inverse Wishart distribution with scalar parameter and parameter matrix .
We use the Fisher information metric to define a measure over the Riemannian manifold formed by the set of Gaussian distributions [
25,
26,
27]. We found these choices for prior and measure worked well for estimating Gaussian distributions for Bayesian quadratic discriminant analysis [
27].
The performance of the proposed Gaussian entropy and relative entropy estimators will depend strongly on the choice of the prior. Generally, prior knowledge or subjective guesses about the data are used to set the parameters of the prior. Another choice to form a prior is to use a coarse estimate of the data, for example, in previous work we found that setting
B equal to the identity matrix times the trace of the sample covariance worked well as a data-adaptive prior in the context of classification [
27]. Since the trace times the identity is the extremal case of maximum entropy Gaussian for a given trace, this specific approach is problematic as a coarse estimate for setting the prior for differential entropy estimation, but other coarse estimates based on a different statistic of the eigenvalue may work well.
5.1. Differential Entropy Estimate of the Gaussian Distribution
Assume
n samples
have been drawn iid from an unknown
d-dimensional normal distribution. Per Proposition 1, we estimate the differential entropy as:
, where the expectation is taken with respect to the posterior distribution over
N and the prior is taken to be inverse Wishart with matrix parameter
and scale parameter
. See the
appendix for full details and derivation. The resulting estimate is,
This estimate is well-defined for any number of samples
n.
5.2. Relative Entropy Estimate between Gaussian Distributions
Assume
samples have been drawn iid from an unknown
d-dimensional normal distribution
, and
samples have been drawn iid from another
d-dimensional distribution
, assumed independent from the first. Then following Proposition 1, we estimate the relative entropy as
where
and
are independent random Gaussians, the expectation is taken with respect to their posterior distributions, and the prior distributions are taken to be inverse Wisharts with scale parameters
and
and matrix parameters
and
. See the
appendix for full details and derivation. The resulting estimate is,
This estimate is well-defined for any number of samples
. If the prior scalar parameters are taken to be the same, that is
, then the digamma terms cancel.
6. Wishart and Inverse Wishart Distributions
The Wishart and inverse Wishart distributions are arguably the most popular distributions for modeling random positive definite matrices. Moreover, if a random variable has a Gaussian distribution, then its sample covariance is drawn from a Wishart distribution. The relative entropy between Wishart distributions may be a useful way to measure the dissimilarity between collections of covariance matrices or Gram (inner product) matrices.
We were unable to find expressions for differential entropy or relative entropy of the Wishart and inverse Wishart distributions, so we first present those, and then present Bayesian estimates of these quantities.
6.1. Wishart Differential Entropy and Relative Entropy
The differential entropy of
W is
The relative entropy between two Wishart distributions
and
with parameters
and
respectively is,
For the special case of , we note that the relative entropy given in (15) is times Stein’s loss function, which is itself a common Bregman divergence.
For the special case of
, we find that the relative entropy between two Wisharts can also be written in the form a Bregman divergence [
21] between
and
. Consider the strictly convex function
, and let
be the derivative of the
. Then (15) becomes,
We term (16) the
log-gamma Bregman divergence. We have not seen this divergence noted before, and hypothesize that this divergence may have physical or practical significance because of the widespread occurrence of the gamma function and its special properties [
28].
6.2. Inverse Wishart Differential Entropy and Relative Entropy
Let
V be distributed according to an inverse Wishart distribution with scalar degree of freedom parameter
and positive definite matrix parameter
as per (
2).
Then
V has differential entropy
The relative entropy between two inverse Wishart distributions with parameters
and
is
One sees that the relative entropy between two inverse Wishart distributions is the same as the relative entropy between two Wishart distributions with inverse matrix parameters
and
respectively. Like the Wishart distribution relative entropy, the inverse Wishart distribution relative entropy has special cases that are the Stein loss and the log-gamma Bregman divergence.
6.3. Bayesian Estimation of Wishart Differential Entropy
We present a Bayesian estimate of the differential entropy of a Wishart distribution p where we make the simplifying assumption that the scalar parameter q is known or estimated (for example, it is common to assume that ). We estimate the differential entropy where the estimation is with respect to the uncertainty in the matrix parameter Σ. We assume the prior is inverse Wishart with scale parameter r and parameter matrix U, which reduces to the non-informative prior when r and U are chosen to be zeros.
Then given sample
matrices
drawn iid from the Wishart
W, the normalized posterior distribution
is inverse Wishart with matrix parameter
and scalar parameter
(details in
Appendix).
Then our differential entropy estimate
where the expectation is with respect to the posterior
is:
6.4. Bayesian Estimation of Relative Entropy between Two Wisharts
We present a Bayesian estimate of the relative entropy between two Wishart distributions and where we make the simplifying assumption that the respective scalar parameters are known or estimated (for example, that ), and then we estimate the relative entropy where the estimation is with respect to the uncertainty in the respective matrix parameters . To this end, we treat the unknown Wishart parameters as random, and compute the estimate . For and we use independent inverse Wishart conjugate priors with respective scalar parameters and parameter matrices , which reduces to non-informative priors when and are chosen to be zeros.
Then given sample matrices drawn iid from the Wishart , and sample matrices drawn iid from the Wishart , the normalized posterior distribution is inverse Wishart with matrix parameter and scalar parameter , and the normalized posterior distribution is inverse Wishart with matrix parameter and scalar parameter .
Then our relative entropy estimate
(where the expectation is with respect to the posterior distributions) is
6.5. Bayesian Estimation of Inverse Wishart Differential Entropy
Let
denote the
ith of
n random iid draws from an inverse unknown Wishart distribution
p with parameters
. Taking the prior
to be a Wishart distribution with parameter
r and
U, our Bayesian estimate of the inverse Wishart differential entropy is
6.6. Bayesian Estimation of Relative Entropy between Two Inverse Wisharts
Given
, and assuming independent Wishart priors with respective scalar parameters
and parameter matrices
, and given
sample
matrices
drawn iid from the inverse Wishart
, and
sample
matrices
drawn iid from the inverse Wishart
, our Bayesian estimate of the relative entropy is
7. Discussion
We have presented Bayesian differential entropy and relative entropy estimates for four standard distributions, and in doing so illustrated techniques that could be used to derive such estimates for other distributions. For the uniform case with no prior, the given estimators perform significantly better than previous estimators, and this experimental evidence validates our approach. However given a prior over distributions, the performance will depend heavily on the accuracy of the prior, and a thorough experimental study would be useful to practitioners but was outside the scope of this investigation.
In practice, there may not be a priori information available to determine a prior, and an open question is how to design appropriate data-dependent priors for differential entropy estimation. For example, for Bayesian quadratic discriminant analysis classification [
27], we have shown that setting the prior matrix parameter for the Gaussian to be a coarse estimate of the data’s covariance (the identity times the trace of the sample covariance) works well. However, for differential entropy estimation the trace forms an extreme estimate, and is thus not (by itself) suitable for forming a data-dependent prior for this problem.
Another open area is forming estimators for more complicated parametric models, for example estimating the differential entropy and relative entropy of Gaussian mixture models. Estimating the differential entropy of Gaussian processes is also an important problem [
29] that may be amenable to the present approach.
Lastly, the new estimators have been motivated by their expected Bregman loss optimality and by the practical consideration of producing estimates even when there are fewer samples than dimensions, but there are a number of theoretical questions about these estimators that are open, such as domination.