Distances in Probability Space and the Statistical Complexity Setup
Abstract
:1. Statistical Complexity Measures
1.1. Meaning of the Concept
1.2. Information Measures
1.3. Distances and Statistical Complexity Measure
- (a)
- Euclidean norm in [11]:This is the “natural” choice (the most simple one) for the distance . We haveThis is the disequilibrium form for the complexity measure proposed by López-Ruiz, Mancini and Calbet (LMC-complexity measure [11]). Such straightforward definition of distance has been criticized by Wootters in an illuminating communication [24] because, in using the Euclidean norm, one is ignoring the fact that we are dealing with a space of probability distributions and thus disregarding the stochastic nature of the distribution P.
- (b)
- The concept of “statistical distance” originates in a quantum mechanical context. One uses it primarily to distinguish among different preparations of a given quantum state, and, more generally, to ascertain to what an extent two such states differ from one another. The concomitant considerations being of an intrinsic statistical nature, the concept can be applied to “any” probabilistic space [24]. The main idea underlying this notion of distance is that of adequately taking into account statistical fluctuations inherent to any finite sample. As a result of the associated statistical errors, the observed frequencies of occurrence of the various possible outcomes typically differ somewhat from the actual probabilities, with the result that, in a given fixed number of trials, two preparations are indistinguishable if the difference between the actual probabilities is smaller than the size of a typical fluctuation [24].
- (c)
- The relative entropy of with respect to associated to Shannons measure is the relative Kullbak-Leibler Shannon entropy, that in the discrete case readsConsider now the probability distribution P and the uniform distribution . The distance between these two distributions, in Kullback-Leiber Shannon terms, will be
- (d)
- In general, the entropic difference does not define an information gain (or divergence) because the difference is not necessarily positive definite. Something else is needed. An important example is provided by Jensen’s divergence, which is a symmetric version of the Kullback-Leibler relative entropy, which in terms of the Shannon entropy can be written as:The Jensen-Shannon divergence verifies the following propertiesMoreover, it square root satisfies the triangle inequalitywhich implies that the square root of the Jensen-Shannon divergence is a metric [27]. Note also that it is defined in terms of entropies and, in consequence, is an extensive quantity in the thermodynamical sense. Thus, the corresponding statistical complexity will be an intensive quantity as well.
1.4. Time Evolution
1.5. Additional Issues
- (1)
- it is neither an intensive nor an extensive quantity.
- (2)
- it vanishes exponentially in the thermodynamic limit for all one-dimensional, finite range systems.
- (3)
- be able to distinguish among different degrees of periodicity;
- (4)
- vanish only for unity periodicity.
- (i)
- able to grasp essential details of the dynamics (i.e., chaos, intermittency, etc.)
- (ii)
- capable of discerning between different degrees of periodicity, and
- (iii)
- an intensive quantity if Jensen’s divergence is used.
2. Methodologies for Selecting PDFs
2.1. PDF Based on Histograms
2.2. PDF Based on Bandt and Pompe’s Methodology
3. The Classical Limit of Quantum Mechanics (a Special Semi-Classical Model)
4. Results and Discussion

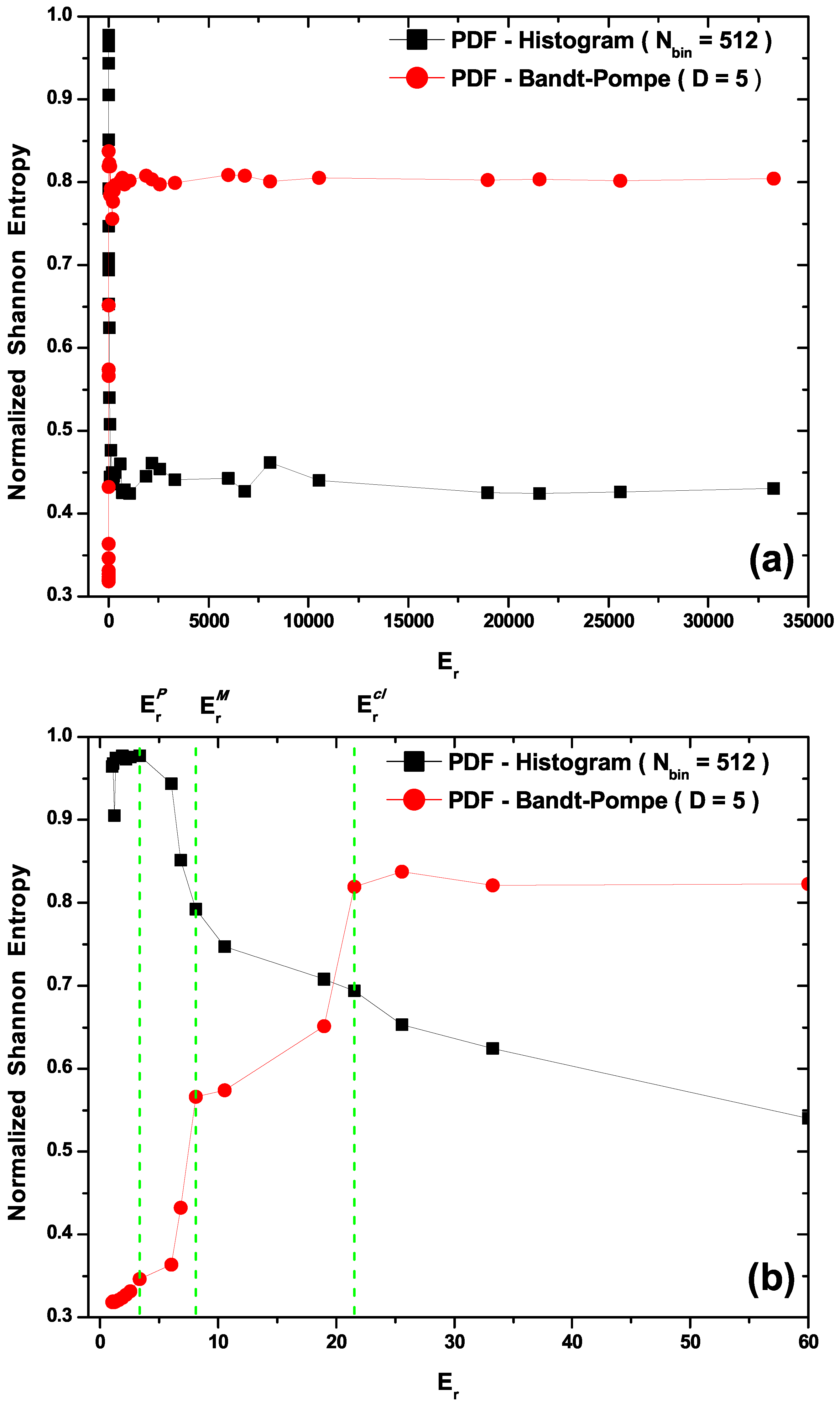
- In Figure 2a,b we plot the Normalized Shannon Entropy, , for PDF histogram and for PDF Bandt and Pompe. Notice in Figure 2a that both definitions tend to different final results for large values. These are the classical results, i.e., the corresponding entropic values calculated using data obtained from the classical versions of Equations (21). Also note in Figure 2b that the PDF histogram’s entropy does not clearly distinguish between transitional and classical sectors. The Bandt and Pompe entropy does distinguish the three process zones and correctly orders entropic sizes according the the physical criteria expounded above (Figure 2b), i.e., it can be said to appropriately represent our three regions.
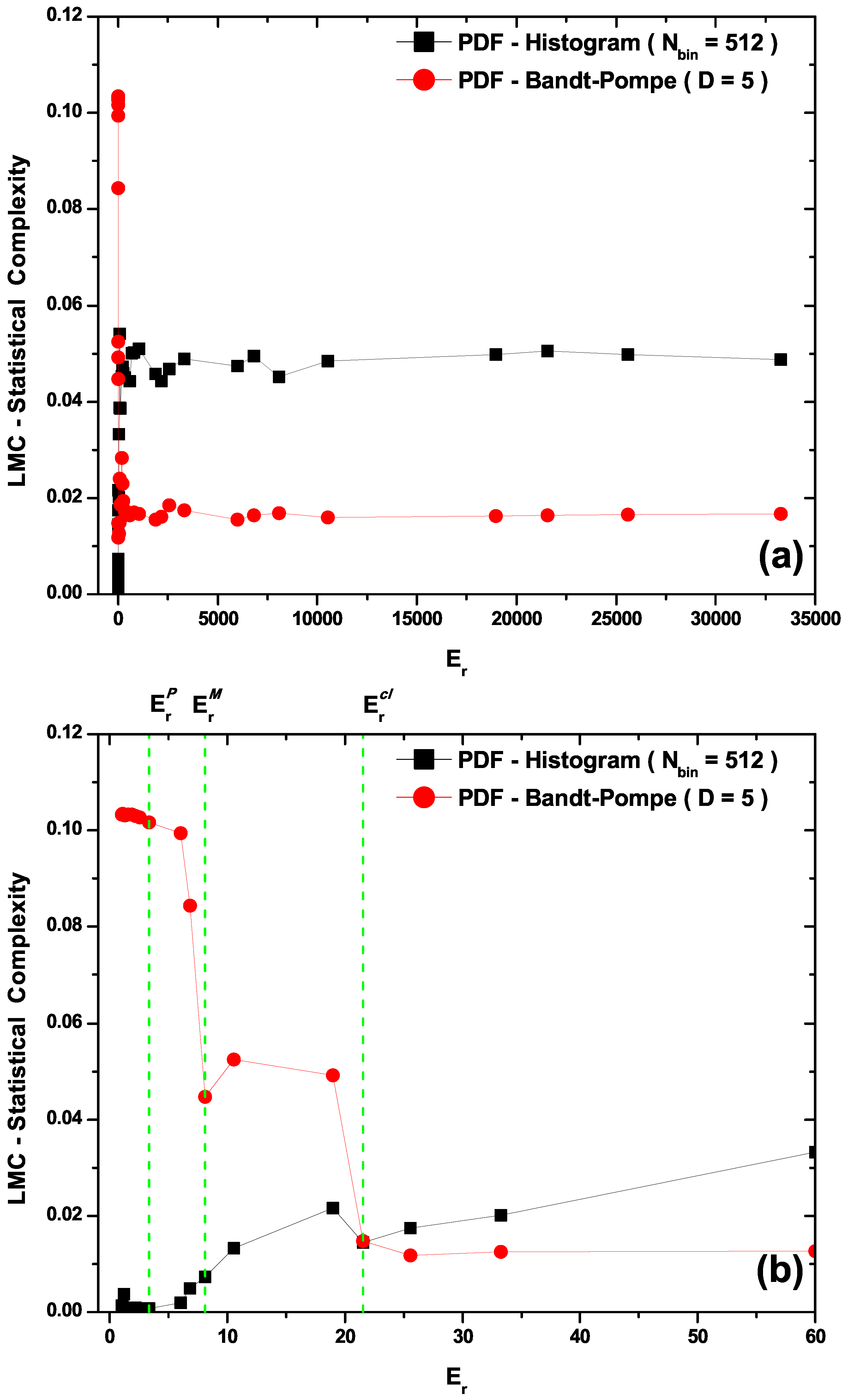
- The LMC statistical complexity, (Figure 3b) does not distinguish between transitional and classical zones in its PDF histogram version, and neither is able to correctly represent the classical sector. Also, the LMC’s PDF Bandt and Pompe version fails to aptly describe the quantal region (see Figure 3b).
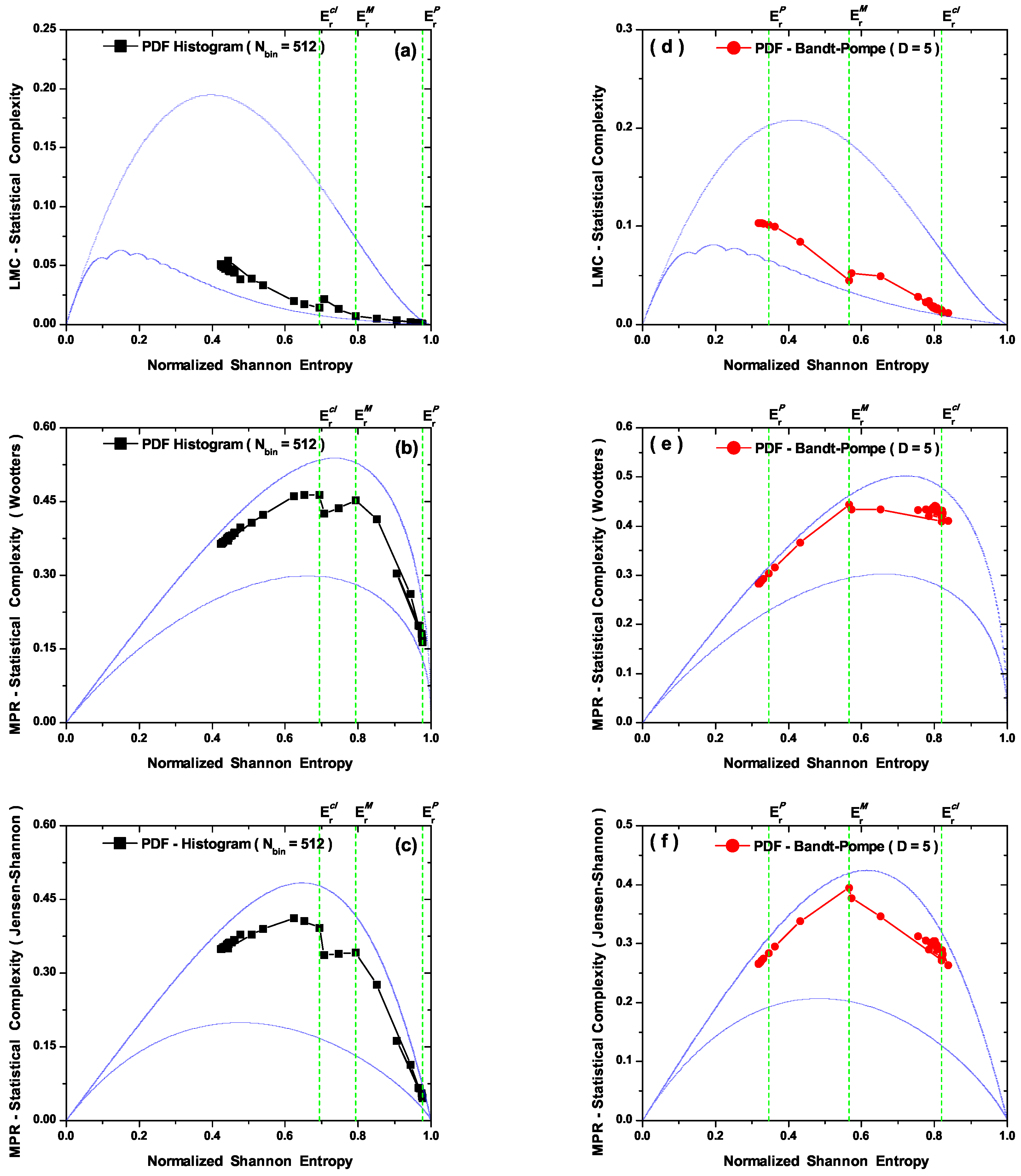
- The MPR statistical complexity with Wooters’ distance (Figure 4b) does distinguish amongst the three zones in its two PDF versions. For the PDF histogram, maximum complexity is attained at . Its quantal sector representation is marred by the fact that one detects complexity values within it larger than those encountered within the transition region (Figure 4b). For the PDF Bandt and Pompe version the associated representation is for all zones grosso modo correct. One would expect, however, that the classical zone’s complexity should not be so similar to that for the transitional one. Note that this classical zone’s complexity is slightly smaller than the maximal complexity attained at (Figure 4b).
- The MPR (Jensen-Shannon) statistical complexity (Figure 4c,d) is quite similar to its MPR (Wootters) counterpart (Figure 4a,b), and distinguishes quite well amongst the three typical regions for both PDF versions, although the quantal representation in the PDF histogram’s case fails, as was the case with the MPR (Wootters) counterpart (Figure 4b), a facet that is improved by the Bandt and Pompe PDF treatment. Consequently, the symbolic MPR (Jensen-Shannon) statistical complexity exhibits the best overall performance (Figure 4d).

5. Conclusions
- The selection of an appropriate disequilibrium distance form .
- The selection of an adequate probability distribution function (PDF).
Acknowledgment
References
- Kowalski, A.M.; Martín, M.T.; Nuñez, J.; Plastino, A.; Proto, A.N. Quantitative indicator for semiquantum chaos. Phys. Rev. A 1998, 58, 2596–2599. [Google Scholar] [CrossRef]
- Kowalski, A.M.; Martín, M.T.; Nuñez, J.; Plastino, A.; Proto, A.N. Semiquantum chaos and the uncertainty principle. Physica A 2000, 276, 95–108. [Google Scholar] [CrossRef]
- Kowalski, A.M.; Plastino, A.; Proto, A.N. Classical limits. Phys. Lett. A 2002, 297, 162–172. [Google Scholar] [CrossRef]
- Kowalski, A.M.; Martín, M.T.; Plastino, A.; Proto, A.N. Classical limit and chaotic regime in a semi-quantum hamiltonian. Int. J. Bifurcation Chaos 2003, 13, 2315–2325. [Google Scholar] [CrossRef]
- Kowalski, A.M.; Martín, M.T.; Plastino, A.; Proto, A.N.; Rosso, O.A. Wavelet statistical complexity analysis of classical limit. Phys. Lett. A 2003, 311, 180–191. [Google Scholar] [CrossRef]
- Kowalski, A.M.; Martín, M.T.; Plastino, A.; Rosso, O.A. Entropic non-triviality, the classical limit, and geometry-dynamics correlations. Int. J. Modern Phys. B 2005, 14, 2273–2285. [Google Scholar] [CrossRef]
- Kowalski, A.M.; Martín, M.T.; Plastino, A.; Rosso, O.A. Bandt-pompe approach to the classical-quantum transition. Physica D 2007, 233, 21–31. [Google Scholar] [CrossRef]
- Lempel, A.; Ziv, j. Complexity of finite sequences. IEEE Trans. Inf. Theory 1976, 22, 75–81. [Google Scholar] [CrossRef]
- Crutchfield, J.P.; Young, K. Inferring statistical complexity. Phys. Rev. Lett. 1989, 63, 105–108. [Google Scholar] [CrossRef] [PubMed]
- Wackerbauer, R.; Witt, R.A.; Atmanspacher, H.; Kurths, J.; Scheingraber, H. A comparative classification of complexity-measures. Chaos Solitons Fractals 1994, 4, 133–173. [Google Scholar] [CrossRef]
- López-Ruiz, L.; Mancini, H.; Calbet, X. A statistical measure of complexity. Phys. Lett. A 1995, 209, 321–326. [Google Scholar] [CrossRef]
- Feldman, D.P.; Crutchfield, J.P. Measures of statistical complexity: Why? Phys. Lett. A 1998, 238, 244–252. [Google Scholar] [CrossRef]
- Shiner, J.S.; Davison, M.; Landsberg, P.T. Simple measure for complexity. Phys. Rev. E 1999, 59, 1459–1464. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Marwan, N.; Wessel, N.; Meyerfeldt, U.; Schirdewan, A.; Kurths, J. Recurrence-plot based measures of complexity and their application to heart-rate-variability data. Phys. Rev. E 2002, 66, 026702. [Google Scholar] [CrossRef]
- Martín, M.T.; Plastino, A.; Rosso, O.A. Statistical complexity and disequilibrium. Phys. Lett. A 2003, 311, 126–132. [Google Scholar] [CrossRef]
- Lamberti, P.W.; Martín, M.T.; Plastino, A.; Rosso, O.A. Intensive entropic nontriviality measure. Physica A 2004, 334, 119–131. [Google Scholar] [CrossRef]
- Rosso, O.A.; Martín, M.T.; Figliola, A.; Keller, K.; Plastino, A. EEG analysis using wavelet-based information tools. J. Neurosci. Meth. 2006, 153, 163–182. [Google Scholar] [CrossRef] [PubMed]
- Grassberger, P. Toward a qualitative theory of self-generated complexity. Int. J. Theor. Phys. 1988, 25, 907–938. [Google Scholar] [CrossRef]
- Kantz, H.; Kurths, J.; Meyer-Kress, G. Nonlinear Analysis of Physiological Data; Springer: Berlin, Germany, 1998. [Google Scholar]
- Rosso, O.A.; De Micco, L.; Larrondo, H.A.; Martín, M.T.; Plastino, A. Generalized statistical complexity measure. Int. J. Bif. Chaos 2010, 20, 775–785. [Google Scholar] [CrossRef]
- Piasecki, R.; Plastino, A. Entropic descriptor of a complex behaviour. Physica A 2010, 389, 397–407. [Google Scholar] [CrossRef]
- Piasecki, R. Microstructure reconstruction using entropic descriptors. Proc. R. Soc. A 2011, 467, 806–820. [Google Scholar] [CrossRef]
- Wootters, K.W. Statistical distance and Hilbert space. Phys. Rev. D 1981, 23, 357–362. [Google Scholar] [CrossRef]
- Basseville, M. Information: Entropies, Divergences et Mayennes; Institut de Recherche en Informatique et Systèmes Aléatoires, Publication Interne 1020. Rennes Cedex: IRISA, 1996. [Google Scholar]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Briët, J.; Harremoës, P. Properties of classical and quantum Jensen-Shannon divergence. Phys. Rev. A 2009, 79, 052311. [Google Scholar] [CrossRef]
- Crutchfield, J.P.; Feldman, D.P.; Shalizi, C.R. Comment I on: simple measure of complexity. Phys. Rev. E 2000, 62, 2996–2997. [Google Scholar] [CrossRef]
- Binder, P.M.; Perry, N. Comment II on: Simple measure of complexity. Phys. Rev. E 2000, 62, 2998–2999. [Google Scholar] [CrossRef]
- Shiner, J.S.; Davison, M.; Landsberg, P.T. Replay to comments on: simple measure for complexity. Phys. Rev. E 2000, 62, 3000–3003. [Google Scholar] [CrossRef]
- Martín, M.T.; Plastino, A.; Rosso, O.A. Generalized statistical complexity measures: Geometrical and analytical properties. Physica A 2006, 369, 439–462. [Google Scholar] [CrossRef]
- Plastino, A.R.; Plastino, A. Symmetries of the Fokker-Plank equation and Fisher-Frieden arrow of time. Phys. Rev. E 1996, 54, 4423–4326. [Google Scholar] [CrossRef]
- Rosso, O.A.; Larrondo, H.A.; Martín, M.T.; Plastino, A.; Fuentes, M.A. Distinguishing noise from chaos. Phys. Rev. Lett. 2007, 99, 154102. [Google Scholar] [CrossRef] [PubMed]
- Anteneodo, C.; Plastino, A.R. Some features of the López-Ruiz-Mancini-Calbet (LMC) statistical measure of complexity. Phys. Lett. A 1996, 223, 348–354. [Google Scholar] [CrossRef]
- Rosso, O.A.; Craig, H.; Moscato, P. Shakespeare and other english renaissance authors as characterized by Information Theory complexity quantifiers. Physica A 2009, 388, 916–926. [Google Scholar] [CrossRef]
- De Micco, L.; González, C.M.; Larrondo, H.A.; Martín, M.T.; Plastino, A.; Rosso, O.A. Randomizing nonlinear maps via symbolic dynamics. Physica A 2008, 387, 3373–3383. [Google Scholar] [CrossRef]
- Mischaikow, K.; Mrozek, M.; Reiss, J.; Szymczak, A. Construction of symbolic dynamics from experimental time series. Phys. Rev. Lett. 1999, 82, 1114–1147. [Google Scholar] [CrossRef]
- Powell, G.E.; Percival, I. A spectral entropy method for distinguishing regular and irregular motion of hamiltonian systems. J. Phys. A: Math. Gen. 1979, 12, 2053–2071. [Google Scholar] [CrossRef]
- Rosso, O.A.; Blanco, S.; Jordanova, J.; Kolev, V.; Figliola, A.; Schürmann, M.; Başar, E. Wavelet entropy: a new tool for analysis of short duration brain electrical signals. J. Neurosc. Meth. 2001, 105, 65–75. [Google Scholar] [CrossRef]
- Bonilla, L.L.; Guinea, F. Collapse of the wave packet and chaos in a model with classical and quantum degrees of freedom. Phys. Rev. A 1992, 45, 7718–7728. [Google Scholar] [CrossRef] [PubMed]
- Cooper, F.; Dawson, J.; Habib, S.; Ryne, R.D. Chaos in time-dependent variational approximations to quantum dynamics. Phys. Rev. E 1998, 57, 1489–1498. [Google Scholar] [CrossRef]
- Keller, K.; Sinn, M. Ordinal analysis of time series. Physica A 2005, 356, 114–120. [Google Scholar] [CrossRef]
- Saco, P.M.; Carpi, L.C.; Figliola, A.; Serrano, E.; Rosso, O.A. Entropy analysis of the dynamics of el Niño/southern oscillation during the holocene. Physica A 2010, 389, 5022–5027. [Google Scholar] [CrossRef]
- Zeh, H.D. Why Bohms quantum theory? Found. Phys. Lett. 1999, 12, 197–200. [Google Scholar] [CrossRef]
- Zurek, W.H. Pointer basis of quantum apparatus: Into what mixture does the wave packet collapse? Phys. Rev. D 1981, 24, 1516–1525. [Google Scholar] [CrossRef]
- Zurek, W.H. Decoherence, einselection, and the quantum origins of the classical. Rev. Mod. Phys. 2003, 75, 715–775. [Google Scholar] [CrossRef]
- Rosso, O.A.; Martín, M.T.; Plastino, A. Evidence of self-organization in brain electrical activity using wavelet-based informational tools. Physica A 2005, 347, 444–464. [Google Scholar] [CrossRef]
- Plastino, A.; Martín, M.T.; Rosso, O.A. Generalized information measures and the analysis of brain electrical signals. In Nonextensive Entropy—Interdisciplinary Applications; Gell-Mann, M., Tsallis, C., Eds.; Oxford University Press: New York, USA, 2004; pp. 261–293. [Google Scholar]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kowalski, A.M.; Martín, M.T.; Plastino, A.; Rosso, O.A.; Casas, M. Distances in Probability Space and the Statistical Complexity Setup. Entropy 2011, 13, 1055-1075. https://doi.org/10.3390/e13061055
Kowalski AM, Martín MT, Plastino A, Rosso OA, Casas M. Distances in Probability Space and the Statistical Complexity Setup. Entropy. 2011; 13(6):1055-1075. https://doi.org/10.3390/e13061055
Chicago/Turabian StyleKowalski, Andres M., Maria Teresa Martín, Angelo Plastino, Osvaldo A. Rosso, and Montserrat Casas. 2011. "Distances in Probability Space and the Statistical Complexity Setup" Entropy 13, no. 6: 1055-1075. https://doi.org/10.3390/e13061055
APA StyleKowalski, A. M., Martín, M. T., Plastino, A., Rosso, O. A., & Casas, M. (2011). Distances in Probability Space and the Statistical Complexity Setup. Entropy, 13(6), 1055-1075. https://doi.org/10.3390/e13061055




