1. Introduction
The role of numerical simulation in science is to work out in detail what our mathematical models of physical systems predict. When the models become too difficult to solve by analytical techniques, or details are required for specific values of parameters, numerical computation can often fill the gap. This is only a practical option if the calculations required can be done efficiently with the resources available. As most computational scientists know well, many calculations we would like to do require more computational power than we have. Running out of computational power is nearly ubiquitous whatever you are working on, but for those working on quantum systems this happens for rather small system sizes. Consequently, there are significant open problems in important areas, such as high temperature superconductivity, where progress is slow because we cannot adequately test our models or use them to make predictions.
Simulating a fully general quantum system on a classical computer is possible only for very small systems, because of the exponential scaling of the Hilbert space with the size of the quantum system. To appreciate just how quickly this takes us beyond reasonable computational resources, consider the classical memory required to store a fully general state
of
n qubits (two-state quantum systems). The Hilbert space for
n qubits is spanned by
orthogonal states, labeled
with
. The
n qubits can be in a superposition of all of them in different proportions,
To store this description of the state in a classical computer, we need to store all of the complex numbers
. Each requires two floating point numbers (real and imaginary parts). Using 32 bits (4 bytes) for each floating point number, a quantum state of
qubits will require 1 Gbyte of memory—a new desktop computer in 2010 probably has around 2 to 4 Gbyte of memory in total. Each additional qubit doubles the memory, so 37 qubits would need a Terabyte of memory—a new desktop computer in 2010 probably has a hard disk of this size. The time that would be required to perform any useful calculation on this size of data is actually what becomes the limiting factor. One of the largest simulations of qubits on record [
1] computed the evolution of 36 qubits in a quantum register using one Terabyte of memory, with multiple computers for the processing. Simulating more than 40 qubits in a fully general superposition state is thus well beyond our current capabilities. Computational physicists can handle larger systems if the model restricts the dynamics to only part of the full Hilbert space. Appropriately designed methods then allow larger classical simulations to be performed [
2]. However, any model is only as good as its assumptions, and capping the size of the accessible part of the Hilbert space below
orthogonal states for all system sizes is a severe restriction.
The genius of Feynman in 1982 was to come up with an idea for how to circumvent the difficulties of simulating quantum systems classically [
3]. The enormous Hilbert space of a general quantum state can be encoded and stored efficiently on a quantum computer using the superpositions it has naturally. This was the original inspiration for quantum computation, independently proposed also by Deutsch [
4] a few years later. The low threshold for useful quantum simulations, of upwards of 36 or so qubits, means it is widely expected to be one of the first practical applications of a quantum computer. Compared to the millions of qubits needed for useful instances of other quantum algorithms, such as Shor’s algorithm for factoring [
5], this is a realistic goal for current experimental research to work towards. We will consider the experimental challenges in the latter sections of this review, after we have laid out the theoretical requirements.
Although a quantum computer can efficiently store the quantum state under study, it is not a “drop in” replacement for a classical computer as far as the methods and results are concerned. A classical simulation of a quantum system gives us access to the full quantum state,
i.e., all the
complex numbers
in Equation (
1). A quantum computer storing the same quantum state can in principle tell us no more than whether one of the
is non-zero, if we directly measure the quantum state in the computational basis. As with all types of quantum algorithm, an extra step is required in the processing to concentrate the information we want into the register for the final measurement. Particularly for quantum simulation, amassing enough useful information also typically requires a significant number of repetitions of the simulation. Classical simulations of quantum systems are usually “strong simulations” [
6,
7] which provide the whole probability distribution, and we often need at least a significant part of this, e.g., for correlation functions, from a quantum simulation. If we ask only for sampling from the probability distribution, a “weak simulation”, then a wider class of quantum computations can be simulated efficiently classically, but may require repetition to provide useful results, just as the quantum computation would. Clearly, it is only worth using a quantum computer when neither strong nor weak simulation can be performed efficiently classically, and these are the cases we are interested in for this review.
As with all quantum algorithms, the three main steps, initialization, quantum processing, and data extraction (measurement) must all be performed efficiently to obtain a computation that is efficient overall. Efficient in this context will be taken to mean using resources that scale polynomially in the size of the problem, although this isn’t always a reliable guide to what can be achieved in practice. For many quantum algorithms, the initial state of the computer is a simple and easy to prepare state, such as all qubits set to zero. However, for a typical quantum simulation, the initial state we want is often an unknown state that we are trying to find or characterise, such as the lowest energy state. The special techniques required to deal with this are discussed in
Section 4. The second step is usually the time evolution of the Hamiltonian. Classical simulations use a wide variety of methods, depending on the model being used, and the information being calculated. The same is true for quantum simulation, although the diversity is less developed, since we don’t have the possibility to actually use the proposed methods on real problems yet and refine through practice. Significant inovation in classical simulation methods arose as a response to practical problems encountered when theoretical methods were put to the test, and we can expect the same to happen with quantum simulation. The main approach to time evolution using a universal quantum computer is described in
Section 2.1, in which the Lloyd method for evolving the Hamiltonian using Trotterization is described. In
Section 5, further techniques are described, including the quantum version of the pseudo-spectral method that converts between position and momentum space to evaluate different terms in the Hamiltonian using the simplest representation for each, and quantum lattice gases, which can be used as a general differential equation solver in the same way that classical lattice gas and lattice Boltzmann methods are applied. It is also possible to take a direct approach, in which the Hamiltonian of the quantum simulator is controlled in such a way that it behaves like the one under study—an idea already well established in the Nuclear Magnetic Resonance (NMR) community. The relevant theory is covered in
Section 2.3. The final step is data extraction. Of course, data extraction methods are dictated by what we want to calculate, and this in turn affects the design of the whole algorithm, which is why it is most naturally discussed before initialization, in
Section 3.
For classical simulation, we rarely use anything other than standard digital computers today. Whatever the problem, we map it onto the registers and standard gate operations available in a commercial computer (with the help of high level programming languages and compilers). The same approach to quantum simulation makes use of the quantum computer architectures proposed for universal quantum computation. The seminal work of Lloyd [
8] gives the conditions under which quantum simulations can be performed efficiently on a universal quantum computer. The subsequent development of quantum simulation algorithms for general purpose quantum computers accounts for a major fraction of the theoretical work in quantum simulation. However, special purpose computational modules are still used for classical applications in many areas, such as fast real time control of experimental equipment, or video rendering on graphics cards to control displays, or even mundane tasks such as controlling a toaster, or in a digital alarm clock. A similar approach can also be used for quantum simulation. A quantum simulator is a device which is designed to simulate a particular Hamiltonian, and it may not be capable of universal quantum computation. Nonetheless, a special purpose quantum simulator could still be fast and efficient for the particular simulation it is built for. This would allow a useful device to be constructed before we have the technology for universal quantum computers capable of the same computation. This is thus a very active area of current research. We describe a selection of these in the experimental
Section 8 to
Section 10, which begins with its own overview in
Section 7.
While we deal here strictly with quantum simulation of quantum systems, some of the methods described here, such as lattice gas automata, are applicable to a wider class of problems, which will be mentioned as appropriate. A short review such as this must necessarily be brief and selective in the material covered from this broad and active field of research. In particular, the development of Hamiltonian simulation applied to quantum algorithms begun by the seminal work of Aharonov and Ta-Shma [
9]—which is worthy of a review in itself—is discussed only where there are implications for practical applications. Where choices had to be made, the focus has been on relevance to practical implementation for solving real problems, and reference has been made to more detailed reviews of specific topics, where they already exist. The pace of development in this exciting field is such that it will in any case be important to refer to more recent publications to obtain a fully up to date picture of what has been achieved.
2. Universal Quantum Simulation
The core processing task in quantum simulation will usually be the time evolution of a quantum system under a given Hamiltonian,
Given the initial state
and the Hamiltonian
, which may itself be time dependent, calculate the state of the system
at time
t. In many cases it is the properties of a system governed by the particular Hamiltonian that are being sought, and pure quantum evolution is sufficient. For open quantum systems where coupling to another system or environment plays a role, the appropriate master equation will be used instead. In this section we will explore how accomplish the time evolution of a Hamiltonian efficiently, thereby explaining the basic theory underlying quantum simulation.
2.1. Lloyd’s Method
Feynman’s seminal ideas [
3] from 1982 were fleshed out by Lloyd in 1996, in his paper on universal quantum simulators [
8]. While a quantum computer can clearly store the quantum state efficiently compared with a classical computer, this is only half the problem. It is also crucial that the computation on this superposition state can be performed efficiently, the more so because classically we actually run out of computational power before we run out of memory to store the state. Lloyd notes that simply by turning on and off the correct sequence of Hamiltonians, a system can be made to evolve according to any unitary operator. By decomposing the unitary operator into a sequence of standard quantum gates, Vartiainen
et al. [
10] provide a method for doing this with a gate model quantum computer. However, an arbitrary unitary operator requires exponentially many parameters to specify it, so we don’t get an efficient algorithm overall. A unitary operator with an exponential number of parameters requires exponential resources to simulate it in both the quantum and classical cases. Fortunately, (as Feynman had envisaged), any system that is consistent with special and general relativity evolves according to local interactions. All Hamiltonian evolutions
with only local interactions can be written in the form
where each of the
n local Hamiltonians
acts on a limited space containing at most
ℓ of the total of
N variables. By “local” we only require that
ℓ remains fixed as
N increases, we don’t require that the
ℓ variables are actually spatially localised, allowing efficient simulation for many non-relativistic models with long-range interactions. The number of possible distinct terms
in the decomposition of
is given by the binomial coefficient
. Thus
is polynomial in
N. This is a generous upper bound in many practical cases: for Hamiltonians in which each system interacts with at most
ℓ nearest neighbours,
.
In the same way that classical simulation of the time evolution of dynamical systems is often performed, the total simulation time
t can be divided up into
τ small discrete steps. Each step is approximated using a Trotter-Suzuki [
11,
12] formula,
The higher order term of order
k is bounded by
, where
is the supremum, or maximum expectation value, of the operator
over the states of interest. The total error is less than
if just the first term in Equation (
4) is used to approximate
. By taking
τ to be sufficiently large the error can be made as small as required. For a given error
ϵ, from the second term in Equation (
4) we have
. A first order Trotter-Suzuki simulation thus requires
.
Now we can check that the simulation scales efficiently in the number of operations required. The size of the most general Hamiltonian
between
ℓ variables depends on the dimensions of the individual variables but will be bounded by a maximum size
g. The Hamiltonians
and
can be time dependent so long as
g remains fixed. Simulating
requires
operations where
is the dimension of the variables involved in
. In Equation (
4), each local operator
is simulated
τ times. Therefore, the total number of operations required for simulating
is bounded by
. Using
, the number of operations
is given by
The only dependence on the system size
N is in
n, and we already determined that
n is polynomial in
N, so the number of operations is indeed efficient by the criterion of polynomial scaling in the problem size.
The simulation method provided by Lloyd that we just described is straightforward but very general. Lloyd laid the groundwork for subsequent quantum simulation development, by providing conditions (local Hamiltonians) under which it will be possible in theory to carry out efficient quantum simulation, and describing an explicit method for doing this. After some further consideration of the way the errors scale, the remainder of this section elaborates on exactly which Hamiltonians in a quantum simulator can efficiently simulate which other Hamiltonians in the system under study.
2.2. Errors and Efficiency
Although Lloyd [
8] explicitly notes that to keep the total error below
ϵ, each operation must have error less than
where
, he does not discuss the implications of this scaling as an inverse polynomial in
N. For digital computation, we can improve the accuracy of our results by increasing the number of bits of precision we use. In turn, this increases the number of elementary (bitwise) operations required to process the data. To keep the errors below a chosen
ϵ by the end of the computation, we must have
accurate bits in our output register. The resources required to achieve this in an efficient computation scale polynomially in
. In contrast, as already noted in Equation (
5), the resources required for quantum simulation are proportional to
, so the dependence on
ϵ is inverse, rather than log inverse.
The consequences of this were first discussed by Brown
et al. [
13], who point out that all the work on error correction for quantum computation assumes a logarithmic scaling of errors with the size of the computation, and they experimentally verify that the errors do indeed scale inversely for an NMR implementation of quantum simulation. To correct these errors thus requires exponentially more operations for quantum simulation than for a typical (binary encoded) quantum computation of similar size and precision. This is potentially a major issue, once quantum simulations reach large enough sizes to solve useful problems. The time efficiency of the computation for any quantum simulation method will be worsened due to the error correction overheads. This problem is mitigated somewhat because we may not actually need such high precision for quantum simulation as we do for calculations involving integers, for example. However, Clark
et al. [
14] conducted a resource analysis for a quantum simulation to find the ground state energy of the transverse Ising model performed on a circuit model quantum computer. They found that, even with modest precision, error correction requirements result in unfeasibly long simulations for systems that would be possible to simulate if error correction weren’t necessary. One of the main reasons for this is the use of Trotterization, which entails a large number of steps
τ each composed of many operations with associated imperfections requiring error correction.
Another consequence of the polynomial scaling of the errors, explored by Kendon
et al. [
15], is that analogue (continuous variable) quantum computers may be equally suitable for quantum simulation, since they have this same error scaling for any computation they perform. This means they are usually considered only for small processing tasks as part of quantum communications networks, where the poor scaling is less of a problem. As Lloyd notes [
8], the same methods as for discrete systems generalise directly onto continuous variable systems and Hamiltonians.
On the other hand, this analysis doesn’t include potential savings that can be made when implementing the Lloyd method, such as by using parallel processing to compute simultaneously the terms in Equation (
3) that commute. The errors due to decoherence can also be exploited to simulate the effects of noise on the system being studied, see
Section 5.4. Nonetheless, the unfavorable scaling of the error correction requirements with system size in quantum simulation remains an under-appreciated issue for all implementation methods.
2.3. Universal Hamiltonians
Once Lloyd had shown that quantum simulation can be done efficiently overall, attention turned to the explicit forms of the Hamiltonians, both the in the system to be simulated, and the available in the quantum computer. Since universal quantum computation amounts to being able to implement any unitary operation on the register of the quantum computer, this includes quantum simulation as a special case, i.e., the unitary operations derived from local Hamiltonians. Universal quantum computation is thus sufficient for quantum simulation, but this leaves open the possibility that universal quantum simulation could be performed equally efficiently with less powerful resources. There is also the important question of how much the efficiency can be improved by exploiting the in the quantum computer directly rather than through standard quantum gates.
The natural idea that mapping directly between the
and the
should be the most efficient way to do quantum simulation resulted in a decade of research that has answered almost all the theoretical questions one can ask about exactly which Hamiltonians can simulate which other Hamiltonians, and how efficiently. The physically-motivated setting for much of this work is a quantum computer with a single, fixed interaction between the qubits, that can be turned on and off but not otherwise varied, along with arbitrary local control operations on each individual qubit. This is a reasonable abstraction of a typical quantum computer architecture: controlled interactions between qubits are usually hard and/or slow compared with rotating individual qubits. Since most non-trivial interaction Hamiltonians can be used to do universal quantum computation, it follows they can generally simulate all others (of the same system size or smaller) as well. However, determining the optimal control sequences and resulting efficiency is computationally hard in the general case [
16,
17,
18], which is not so practical for building actual universal quantum simulators. These results are thus important for the theoretical understanding of the interconvertability of Hamiltonians, but for actual simulator design we will need to choose Hamiltonians
for which the control sequences can be obtained efficiently.
Dodd
et al. [
19], Bremner
et al. [
20], and Nielsen
et al. [
21] characterised non-trivial Hamiltonians as entangling Hamiltonians, in which every subsystem is coupled to every other subsystem either directly or via intermediate subsystems. When the subsystems are qubits (two-state quantum systems), multi-qubit Hamiltonians involving an even number of qubits provide universal simulation, when combined with local unitary operations. Qubit Hamiltonians where the terms couple only odd numbers of qubits are universal for the simulation of one fewer logical qubits (using a special encoding) [
22]. When the subsystems are qudits (quantum systems of dimension
d), any two-body qudit entangling Hamiltonian is universal, and efficiently so, when combined with local unitary operators [
21]. This is a useful and illuminating approach because of the fundamental role played by entanglement in quantum information processing. Entanglement can only be generated by interaction (direct or indirect) between two (or more) parties. The local unitaries and controls can thus only move the entanglement around, they cannot increase it. These results show that generating enough entanglement can be completely separated from the task of shaping the exact form of the Hamiltonian. Further work on general Hamiltonian simulation has been done by McKague
et al. [
23] who have shown how to conduct a multipartite simulation using just a real Hilbert space. While not of practical importance, this is significant in relation to foundational questions. It follows from their work that Bell inequalities can be violated by quantum states restricted to a real Hilbert space. Very recent work by Childs
et al. [
24] fills in most of the remaining gaps in our knowledge of the conditions under which two-qubit Hamiltonians are universal for approximating other Hamiltonians (equally applicable to both quantum simulation and computation). There are only three special types of two-qubit Hamiltonians that aren’t universal for simulating other two-qubit Hamiltonians, and some of these are still universal for simulating Hamiltonians on more than two qubits.
2.4. Efficient Hamiltonian Simulation
The other important question about using one Hamiltonian to simulate another is how efficiently it can be done. The Lloyd method described in
Section 2.1 can be improved to bring the scaling with
t down from quadratic, Equation (
5), to close to linear by using higher order terms from the Trotter-Suzuki expansion [
11]. This is close to optimal, because it is not possible to perform simulations in less than linear time, as Berry
et al. [
25] prove. They provide a formula for the optimal number
of higher order terms to use, trading off extra operations per step
τ for less steps due to the improved accuracy of each step,
where
is the spectral norm of
(equal to the magnitude of the largest eigenvalue for Hermitian matrices). The corresponding optimal number of operations is bounded by
This is close to linear for large
. Recent work by Papageorgiou and Zhang [
26] improves on Berry
et al.’s results, by explicitly incoporating the dependence on the norms of the largest and next largest of the
in Equation (
3).
Berry
et al. [
25] also consider more general Hamiltonians, applicable more to quantum algorithms than quantum simulation. For a sparse Hamiltonian,
i.e., with no more than a fixed number of nonzero entries in each column of its matrix representation, and a black box function which provides one of these entries when queried, they derive a bound on the number of calls to the black box function required to simulate the Hamiltonian
. When
is bounded by a constant, the number of calls to obtain matrix elements scales as
where
n is the number of qubits necessary to store a state from the Hilbert space on which
acts, and
is the iterative log function, the number of times log has to be applied until the result is less than or equal to one. This is a very slowly growing function, for practical values of
n it will be less than about five. This scaling is thus almost optimal, since (as already noted) sub-linear time scaling is not possible. These results apply to Hamiltonians where there is no tensor product structure, so generalise what simulations it is possible to perform efficiently. Child and Kothari [
27,
28] provide improved methods for sparse Hamiltonians by decomposing them into sums where the graphs corresponding to the non-zero entries are star graphs. They also prove a variety of cases where efficient simulation of non-sparse Hamiltonians is possible, using the method developed by Childs [
29] to simulate Hamiltonians using quantum walks. These all involve conditions under which an efficient description of a non-sparse Hamiltonian can be exploited to simulate it. While of key importance for the development of quantum algorithms, these results don’t relate directly to simulating physical Hamiltonians.
If we want to simulate bipartite (
i.e., two-body) Hamiltonians
using only bipartite Hamiltonians
, the control sequences can be efficiently determined [
17,
18,
30]. Dür, Bremner and Briegel [
31] provide detailed prescriptions for how to map higher-dimensional systems onto pairwise interacting qubits. They describe three techniques: using commutators between different
to build up higher order interactions; graph state encodings; and teleportation-based methods. All methods incur a cost in terms of resources and sources of errors, which they also analyse in detail. The best choice of technique will depend on the particular problem and type of quantum computer available.
The complementary problem: given two-qubit Hamiltonians, how can higher dimensional qubit Hamiltonians be approximated efficiently, was tackled by Bravyi
et al. [
32]. They use perturbation theory gadgets to construct the higher order interactions, which can be viewed as a reverse process to standard perturbation theory. The generic problem of
ℓ-local Hamiltonians in an algorithmic setting is known to be NP-hard for finding the ground state energy, but Bravyi
et al. apply extra constraints to restrict the Hamiltonians of both system and simulation to be physically realistic. Under these conditions, for many-body qubit Hamiltonians
with a maximum of
ℓ interactions per qubit, and where each qubit appears in only a constant number of the
terms, Bravyi
et al. show that they can be simulated using two-body qubit Hamiltonians
with an absolute error given by
; where
ϵ is the precision,
the largest norm of the local interactions and
n is the number of qubits. For physical Hamiltonians, the ground state energy is proportional to
, allowing an efficient approximation of the ground state energy with arbitrarily small relative error
ϵ.
Two-qubit Hamiltonians
with local operations are a natural assumption for modelling a quantum computer, but so far we have only discussed the interaction Hamiltonian. Vidal and Cirac [
33] consider the role of and requirements for the local operations in more detail, by adding ancillas-mediated operations to the available set of local operations. They compare this case with that of local operations and classical communication (LOCC) only. For a two-body qubit Hamiltonian, the simulation can be done with the same time efficiency, independent of whether ancillas are used, and this allows the problem of time optimality to be solved [
30]. However, for other cases using ancillas gives some extra efficiency, and finding the time optimal sequence of operations is difficult. Further work on time optimality for the two qubit case by Hammerer
et al. [
34] and Haselgrove
et al. [
35] proves that in most cases, a time optimal simulation requires an infinite number of infinitesimal time steps. Fortunately, they were also able to show that using finite time steps gives a simulation with very little extra time cost compared to the optimal simulation. This is all good news for the practical feasibility of useful quantum simulation.
The assumption of arbitrary efficient local operations and a fixed but switchable interaction is not experimentally feasible in all proposed architectures. For example, NMR quantum computing has to contend with the extra constraint that the interaction is always on. Turning it off when not required has to be done by engineering time-reversed evolution using local operations. The NMR community has thus developed practical solutions to many Hamiltonian simulation problems of converting one Hamiltonian into another. In turn, much of this is based on pulse sequences originally developed in the 1980s. While liquid state NMR quantum computation is not scalable, it is an extremely useful test bed for most quantum computational tasks, including quantum simulation, and many of the results already mentioned on universal Hamiltonian simulation owe their development to NMR theory [
16,
19,
30]. Leung [
36] gives explicit examples of how to do time reversed Hamiltonians for NMR quantum computation. Experimental aspects of NMR quantum simulation are covered in
Section 8.1.
The assumption of arbitrary efficient local unitary control operations also may not be practical for realistic experimental systems. This is a much bigger restriction than an always on interaction, and in this case it may only be possible to simulate a restricted class of Hamiltonians. We cover some examples in the relevant experimental sections.
3. Data Extraction
So far, we have discussed in a fairly abstract way how to evolve a quantum state according to a given Hamiltonian. While the time evolution itself is illuminating in a classical simulation, where the full description of the wavefunction is available at every time step, quantum simulation gives us only very limited access to the process. We therefore have to design our simulation to provide the information we require efficiently. The first step is to manage our expectations: the whole wavefunction is an exponential amount of information, but for an efficient simulation we can extract only polynomial-sized results. Nonetheless, this includes a wide range of properties of quantum systems that are both useful and interesting, such as energy gaps [
37]; eigenvalues and eigenvectors [
38]; and correlation functions, expectation values and spectra of Hermitian operators [
39]. These all use related methods, including phase estimation or quantum Fourier transforms, to obtain the results. Brief details of each are given below in
Section 3.1 to
Section 3.3.
As will become clear, we may need to use the output of one simulation as the input to a further simulation, before we can obtain the results we want. The distinction between input and output is thus somewhat arbitrary, but since simulation algorithm design is driven by the desired end result, it makes sense to discuss the most common outputs first.
Of course, many other properties of the quantum simulation can be extracted using suitable measurements. Methods developed for experiments on quantum systems can be adapted for quantum simulations, such as quantum process tomography [
40] (though this has severe scaling problems beyond a few qubits), and the more efficient direct characterisation method of Mohseni and Lidar [
41]. Recent advances in developing polynomially efficient measurement processes, such as described by Emerson
et al. [
42], are especially relevant. One well-studied case where a variety of other parameters are required from the simulation is quantum chaos, described in
Section 3.4.
3.1. Energy Gaps
One of the most important properties of an interacting quantum system is the energy gap between the ground state and first excited state. To obtain this using quantum simulation, the system is prepared in an initial state that is a mixture of the ground and first excited state (see
Section 4.2). A time evolution is then performed, which results in a phase difference between the two components that is directly proportional to the energy gap. The standard phase estimation algorithm [
43], which uses the quantum Fourier transform, can then be used to extract this phase difference. The phase estimation algorithm requires that the simulation (state preparation, evolution and measurement) is repeated a polynomial number of times to produce sufficient data to obtain the phase difference. An example, where this method is described in detail for the BCS Hamiltonian, is given by Wu
et al. [
37]. The phase difference can also be estimated by measuring the evolved state using any operator
such that
. where
is the ground state and
the first excited state. Usually this will be satisfied for any operator that does not commute with the Hamiltonian, giving useful experimental flexibility. A polynomial number of measurements are made, for a range of different times. The outcomes can then be classically Fourier transformed to obtain the spectrum, which will have peaks at both zero and the gap [
13]. There will be further peaks in the spectrum if the initial state was not prepared perfectly and had a proportion of higher states mixed in. This is not a problem, provided the signal from the gap frequency can be distinguished, which in turn depends on the level of contamination with higher energy states. However, in the vicinity of a quantum phase transition, the gap will become exponentially small. It is then necessary to estimate the gap for a range of values of the order parameter either side of the phase transition, to identify when it is shrinking below the precision of the simulation. This allows the location of the phase transition to be determined, up to the simulation precision.
3.2. Eigenvalues and Eigenvectors
Generalising from both the Lloyd method for the time evolution of Hamiltonians and the phase estimation method for finding energy gaps, Abrams and Lloyd [
38] provided an algorithm for finding (some of) the eigenvalues and eigenvectors of any Hamiltonian
for which
can be efficiently simulated. Since
and
share the same eigenvalues and eigenvectors, we can equally well use
to find them. Although we can only efficiently obtain a polynomial fraction of them, we are generally only interested in a few, for example the lowest lying energy states.
The Abrams-Lloyd scheme requires an approximate eigenvector
, which must have an overlap
with the actual eigenvector
that is not exponentially small. For low energy states, an approximate adiabatic evolution could be used to prepare a suitable
, see
Section 4.2. The algorithm works by using an index register of
m qubits initialised into a superposition of all numbers 0 to
. The unitary
is then conditionally applied to the register containing
a total of
k times, where
k is the number in the index register. The components of
in the eigenbasis of
now each have a different phase and are entangled to a different index component. An inverse quantum Fourier transform transfers the phases into the index register which is then measured. The outcome of the measurement yields one of the eigenvalues, while the other register now contains the corresponding eigenvector
. Although directly measuring
won’t yield much useful information, it can be used as the input to another quantum simulation process to analyse its properties.
3.3. Correlation Functions and Hermitian Operators
Somma
et al. [
39] provide detailed methods for extracting correlation functions, expectation values of Hermitian operators, and the spectrum of a Hermitian operator. A similar method is employed for all of these, we describe it for correlation functions. A circuit diagram is shown in
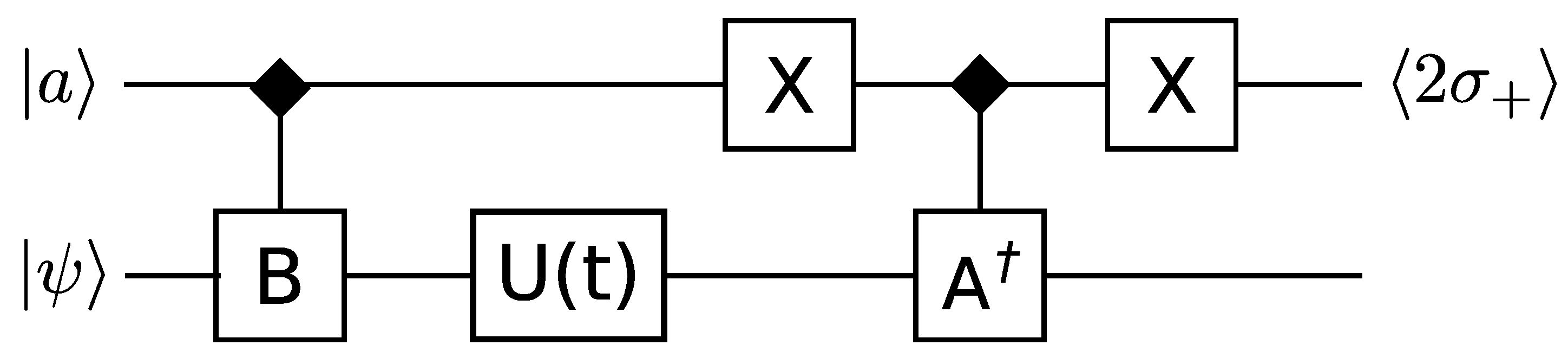
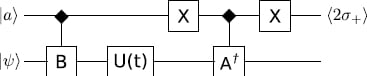
Figure 1.
This circuit can compute correlation functions of the form
where
is the time evolution of the system, and
and
are expressible as a sum of unitary operators. The single qubit ancilla
, initially in the state
, is used to control the conditional application of
and
, between which the time evolution
is performed. Measuring
then provides an estimate of the correlation function to one bit of accuracy. Repeating the computation will build up a more accurate estimate by combining all the outcomes. By replacing
with the space translation operator, spatial correlations instead of time correlations can be obtained.
3.4. Quantum Chaos
The attractions of quantum simulation caught the imagination of researchers in quantum chaos relatively early in the development of quantum computing. Even systems with only a few degrees of freedom and relatively simple Hamiltonians can exhibit chaotic behaviour [
44]. However, classical simulation methods are of limited use for studying quantum chaos, due to the exponentially growing Hilbert space. One of the first quantum chaotic systems for which an efficient quantum simulation scheme was provided is the quantum baker’s transformation. Schack [
45] demonstrates that it is possible to approximate this map as a sequence of simple quantum gates using discrete Fourier transforms. Brun and Schack [
46] then showed that the quantum baker’s map is equivalent to a shift map and numerially simulated how it would behave on a three qubit NMR quantum computer.
While the time evolution methods for chaotic dynamics are straightforward, the important issue is how to extract useful information from the simulation. Using the kicked Harper model, Lévi and Georgeot [
47] extended Schack’s Fourier transform method to obtain a range of characteristics of the behaviour in different regimes, with a polynomial speed up. Georgeot [
48] discusses further methods to extract information but notes that most give only a polynomial increase in efficiency over classical algorithms. Since classical simulations of quantum chaos are generally exponentially costly, it is disappointing not to gain exponentially in efficiency in general with a quantum simulation. However, there are some useful exceptions: methods for deciding whether a system is chaotic or regular using only one bit of information have been developed by Poulin
et al. [
49], and also for measuring the fidelity decay in an efficient manner [
50]. A few other parameters, such as diffusion constants, may also turn out to be extractable with exponential improvement over classical simulation. A review of quantum simulations applied to quantum chaos is provided by Georgeot [
51].
7. Overview
As we have seen, while algorithms for quantum simulation are interesting in their own right, the real drive is towards actual implementations of a useful size to apply to problems we cannot solve with classical computers. The theoretical studies show that quantum simulation can be done with a wide variety of methods and systems, giving plenty of choices for experimentalists to work with. Questions remain around the viability of longer simulations, where errors may threaten the accuracy of the results, and long sequences of operations run beyond the available coherence times. As with quantum computing in general, the main challenge for scaling up is controlling the decoherence and correcting the errors that accumulate from imperfect control operations. Detailed treatment of these issues is beyond the scope of this review and well-covered elsewhere (see, for example, Devitt
et al. [
90]). The extra concern for quantum simulation lies in the unfavorable scaling of errors with system size, as discussed in
Section 2.2.
In
Section 2 we described how to obtain universal quantum simulation from particular sets of resources, mainly a fixed interaction with local unitary controls. Building a universal quantum simulator will allow us to efficiently simulate any quantum system that has a local or efficiently describable Hamiltonian. On the other hand, the generality of universal simulation may not be necessary if the problem we are trying to solve has a specific Hamiltonian with properties or symmetries we can exploit to simplify the simulation. If the Hamiltonian we want to simulate can be matched with a compatible interaction Hamiltonian in the quantum simulator, then there are are likely to be further efficiencies available through simpler control sequences for converting one into the other. From the implementation perspective, a special purpose simulator may be easier to build and operate, a big attraction in these early stages of development. Most architectures for quantum computing are also suitable for universal quantum simulation. However, the range of experimental possibilities is broader if we are willing to specialise to the specific Hamiltonians in the quantum simulator. This allows more to be achieved with the same hardware, and is thus the most promising approach for the first useful quantum simulations.
Buluta and Nori [
91] give a brief overview of quantum simulation that focuses on the various possible architectures and what sort of algorithms these could be used for. There is broad overlap of relevant experimental techniques with those for developing quantum computers in general, and many issues and considerations are common to all applications of quantum computers. In this paper, we concentrate on implementations that correspond to the theoretical aspects we have covered. Many experimental implementations of quantum simulation to date have been in NMR quantum computers. This is not a scalable architecture, but as a well-developed technology it provides an invaluable test bed for small quantum computations. Optical schemes based on entangled photons from down-conversion have also been used to implement a variety of small quantum simulations, but since photons don’t normally interact with each other, they don’t provide a natural route to special purpose quantum simulators. We describe the lessons learned from these quantum simulations in
Section 8. We then turn to simulators built by trapping arrays of ions, atoms, and electrons in
Section 9 and
Section 10. Most of these have applications both as universal quantum simulators and for specific Hamiltonians, with promising experiments and rapid progress being made with a number of specific configurations.
9. Atom Trap and Ion Trap Architectures
Among the architectures for quantum computing predicted to be the most scalable, qubits based on atoms or ions in trap systems are strongly favoured [
107,
108]. Locating the atoms or ions in a trap allows each qubit to be distinguished, and in many cases individually controlled. Review of the many designs that are under development is beyond the scope of this article; while any design for a quantum computer is also suitable for quantum simulation, we focus here on arrays of atoms or ions where the intrinsic coupling between them can be exploited for quantum simulation.
Trapped ions form a Coulomb crystal due to their mutual repulsion, which separates them sufficiently to allow individual addressing by lasers. Coupling between them can be achieved via the vibrational modes of the trap, or mediated by the controlling lasers. Atoms in optical lattices formed by counter-propagating laser beams are one of the most promising recent developments. Once the problem of loading a single atom into each trap was overcome by exploiting the Mott transition [
109], the road was clear for developing applications to quantum computing and quantum simulation. For comprehensive reviews of experimental trap advances, see Wineland [
110] for ion trapping, and Bloch
et al. [
111] for cold atoms.
Jané
et al. [
112] consider quantum simulation using both neutral atoms in an optical lattice and ions stored in an array of micro traps. This allows them to compare the experimental resources required for each scheme, as well as assessing the feasibility of using them as a universal quantum simulator. Atoms in optical lattices have the advantage that there is a high degree of parallelism in the manipulation of the qubits. The difficulty of individually addressing each atom, due to the trap spacing being of the same order as the wavelength of the control lasers, can be circumvented in several ways. If the atoms are spaced more widely, so only every fifth or tenth trap is used, for example, then individual laser addressing can be achieved. Applied fields that intersect at the target atom can also be used to shift the energy levels such that only the target atom is affected by the control laser. Jané
et al. conclude that both architectures should be suitable for quantum simulation.
An alternative approach is to avoid addressing individual atoms altogether. Kraus
et al. [
113] explore the potential of simulations using only global single-particle and nearest neighbor interactions. This is a good approximation for atoms in optical lattices, and the three types of subsystem they consider—fermions, bosons, and spins—can be realised by choosing different atoms to trap in the optical lattice and tuning the lattice parameters to different regimes. They make the physically reasonable assumption that the interactions are short range and translationally invariant. They also apply an additional constraint of periodic boundary conditions, to simplify the analysis. Most physical systems have open rather than periodic boundary conditions, so their results may not be immediately applicable to experiments. For a quadratic Hamiltonian acting on fermions or bosons in a cubic lattice, Kraus
et al. found that generic nearest neighbor interactions are universal for simulating any translationally invariant interaction when combined with all on-site Hamiltonians (the equivalent of any local unitary) provided the interactions acted along both the axes and diagonals of the cubic lattice (compare lattice gases,
Section 5.2). However, for spins in a cubic lattice, there is no set of nearest-neighbor interactions which is universal and not even all next-to-nearest neighbor interactions could be simulated from nearest-neighbor interactions. It is possible that different encodings to those used by Kraus
et al. could get around this restriction, but the full capabilities of spin systems on a cubic lattice remains an open problem. Their results demonstrate that schemes which don’t provide individual addressability can still be useful for simulating a large class of Hamiltonians.
Coupled cavity arrays are a more recent development, combining the advantages a cavity confers in controlling an atom with the scalability of micro-fabricated arrays. While there is a trade off between the relative advantages of the various available trapping architectures, with individual addressability and greater control resulting in systems with a poorer scaling in precision, each scheme has its own advantages and the experiments are still in the very early stages.
9.1. Ion Trap Systems
The greater degree of quantum control available for ions in traps, compared with atoms in optical lattices, means that research on using ion traps for simulating quantum systems is further developed. Clark
et al. [
114] and Buluta and Hasegawa [
115] present designs based on planar RF traps that are specifically geared towards quantum simulations. They focus on producing a square lattice of trapped ions, but their results can be generalised to other shapes such as hexagonal lattices (useful for studying systems such as magnetic frustration). Clark
et al. carried out experimental tests on single traps that allowed them to verify their numerical models of the scheme are accurate. They identify a possible difficulty when it is scaled to smaller ion-ion distances. As the ion spacing decreases, the secular frequency increases, which may make it difficult to achieve coupling strengths that are large relative to the decoherence rate.
As with the simulations done with NMR computers, some of the earliest work on ion trap simulators has focused on the simulation of spin systems. Deng
et al. [
116] and Porras and Cirac [
117,
118] discuss the application of trapped ions to simulate the Bose-Hubbard model, and Ising and Heisenberg interactions. This would allow the observation and analysis of the quantum phase transitions which occur in these systems. They mention three different method for trapping ions that could be used to implement their simulation schemes. Arrays of micro ion traps and linear Paul traps use similar experimental configurations, although Paul traps allow a long range interaction that micro ion trap arrays don’t. Both schemes are particularly suited to simulating an interaction of the form XYZ. Penning traps containing two-dimensional Coulomb crystals could also be used, and this would allow hexagonal lattices to be applied to more complex simulations, such as magnetic frustration. Alternatively [
118], the phonons in the trapped ions can be viewed as the system for the simulation. Within the ion trap system phonons can neither be created nor destroyed, so it is possible to simulate systems such as Bose-Einstein condensates, which is more difficult using qubit systems.
Friedenauer
et al. [
119] have experimentally simulated a quantum phase transition in a spin system using two trapped ions. The system adiabatically traverses from the quantum paramagnetic regime to the quantum (anti)-ferromagnetic regime, with all the parameters controlled using lasers and RF fields. To extract data over the full parameter range the experiment was repeated
times, to obtain good statistics for the probability distributions. While the simulation method is scalable, involving global application of the control fields, it isn’t clear the data extraction methods are practical for larger simulations. This work is significant for being one of the few detailed proof-of-concept experimental studies done in a system other than NMR, and demonstrates the progress made in developing other architectures. In Gerritsma
et al. [
120], they simulate the Klein paradox, in which electrons tunnel more easily through higher barriers than low ones, by precisely tuning the parameters in their trapped ion system. Edwards
et al. [
121] have simulated an Ising system with a transverse field using three trapped ions. They alter the Hamiltonian adiabatically to study a wide range of ground state parameters, thereby mapping out the magnetic phase diagram. This system is scalable up to many tens of ions, which would reach regimes currently inaccessible to classical computation, allowing behavior towards the thermodynamic limit to be studied in detail for general and inhomogeneous spin systems.
Proof-of-principle simulations have also been done with single ions. While less interesting than coupled ions, because the coupled systems are where the Hilbert space scaling really favours quantum simulations, these still test the controls and encoding required. For example, Gerritsma
et al. [
122] simulated the Dirac equation using a single trapped ion, to model a relativistic quantum particle. The high level of control the ion trap provides allows information about regimes and effects that are difficult to simulate classically such as Zitterbewegung.
9.2. Atoms in Optical Lattices
Atoms trapped in the standing waves created by counter-propagating lasers are one of the most exciting recent developments in quantum computing architectures. Their potential for the quantum simulation of many-body systems was obvious from the beginning, and has been studied by many groups since the initial work of Jané
et al. [
112]. Trotzky
et al. [
123] compare optical lattice experimental data with their own classical Monte Carlo simulations, to validate the optical lattice as a reliable model for quantum simulations of ultra-cold strongly interacting Bose gases. They find good agreement for system sizes up to the limit of their simulations of
particles.
The most promising way to use atoms in optical lattices for quantum simulation is as a special purpose simulator, taking advantage of the natural interactions between the atoms. This will allow larger systems to be simulated well before this becomes possible with universal quantum computers. The following three examples illustrate the potential for thinking creatively when looking for the best methods to simulate difficult systems or regimes. Johnson
et al. [
124] discuss the natural occurrence of effective three-body and higher order interactions in two-body collisions between atoms in optical lattices. They use these to explain experimental results showing higher-than-expected decoherence rates. Tuning these many-body interactions could be done using Feshbach resonance control or manipulating the lattice potentials, allowing them to be used for the simulation of effective field theories, see
Section 5.2. Ho
et al. [
125] propose that simulating the repulsive Hubbard model is best done using the attractive Hubbard model, which should be easier to access experimentally. Mapping between different regimes in the same model should be simpler to implement, allowing access to results that are usually difficult experimentally. As with the trapped ion schemes, one of the most common subjects for simulation is many-body quantum phase transitions. Kinoshita
et al. [
126] use rubidium-87 atoms trapped in a combination of two light traps. By altering the trap strengths, the interactions between the atoms can be controlled, allowing them to behave like a one-dimensional Tonks-Girardeau gas through to a Bose-Einstein condensate. They find very good agreement with theoretical predictions for a 1D Bose gas. This is a good example of a special purpose simulator, since there are no individual controls on the atoms, allowing only regimes dictated by the globally controlled coupling to be realised.
9.3. Atoms in Coupled Cavity Arrays
Optical lattices are not the only way to trap arrays of atoms. Coupled cavity arrays offer control over individual atoms much more conveniently than with optical lattices. In coupled cavities the qubits are represented by either polaritons or hyperfine ground state levels, with the former allowing continuous control, and the latter individual addressability. The cavities themselves are an artificial system grown on a microchip in which the qubits on the chip interact with the field mode of the cavity, and the cavities are coupled by the exchange of photons. A simulation of the Heisenberg model is generally one of the earliest proof-of-principle simulations for a new architecture, and Cho
et al. [
127] propose a technique to allow these coupled cavity arrays to do this. Their method should apply generally to different physical implementations of micro cavities. Kay
et al. [
128] and Chen
et al. [
129] both discuss implementation of the Heisenberg model in specific coupled cavity architectures. They confirm that control over nearest and next-nearest neighbour coupling can be achieved, but without short control pulses only global controls are available. Schemes that give individual addressability need short control pulses to modify the intrinsic interactions. These may necessitate the use of the Trotter approximation, making it more difficult to obtain high precision results in cavity arrays. Ivanov
et al. [
130] look at exploiting the polaritons in couple cavity arrays to simulate phase transitions, in the same way as Porras and Cirac [
118] consider using phonons in ion traps. These proposals show the versatility and potential of coupled cavity arrays for further development.
11. Outlook
Quantum simulation is one of the primary short- to mid-term goals of many research groups focusing on quantum computation. The potential advances that even a modest quantum simulator would unleash are substantial in a broad range of fields, from material science (high temperature superconductors and magnetic materials) to quantum chemistry. Quantum simulations are particular promising for simulating fermionic many-body systems and their phase transitions, where the “sign problem” limits efficient classical numerical approximation techniques. Larger quantum simulators could tackle problems in lattice QCD that currently consume a sizable fraction of scientific computing power, while quantum simulations of quantum chemistry have wide-ranging applications reaching as far as the design of molecules for new drugs. We have seen that the theoretical foundations have been laid quite comprehensively, providing detailed methods for efficient quantum simulators, and calculations that confirm their viability.
One significant issue that remains to be fully addressed is the precision requirements for larger scale quantum simulations. Due to the one-to-one mapping between the Hilbert space of the system and the Hilbert space of the quantum simulator, the resources required for a given precision scale inversely with the precision. Compared with digital (classical and qubit) computations, this is exponentially more costly. When combined with the long control sequences required by Trotterization, this threatens the viability of such simulations of even fairly modest size.
Special purpose quantum simulators designed with similar Hamiltonians to the quantum system being studied are the front runners for actually performing a useful calculation beyond the reach of conventional computers. These come in many forms, matching the variety of common Hamiltonians describing physical systems. Among the most developed and versatile, ion traps and atoms in optical lattices are currently in the lead, although micro-fabrication techniques are allowing more sophisticated solid state trap arrays to catch up fast. Actual experimental systems capable of quantum simulations of a significant size are still in the future, but the designs and proof-of-concept experiments already on the table provide a strong base from which to progress on this exciting challenge.