Maximum Entropy Production as an Inference Algorithm that Translates Physical Assumptions into Macroscopic Predictions: Don’t Shoot the Messenger
Abstract
:1. Introduction
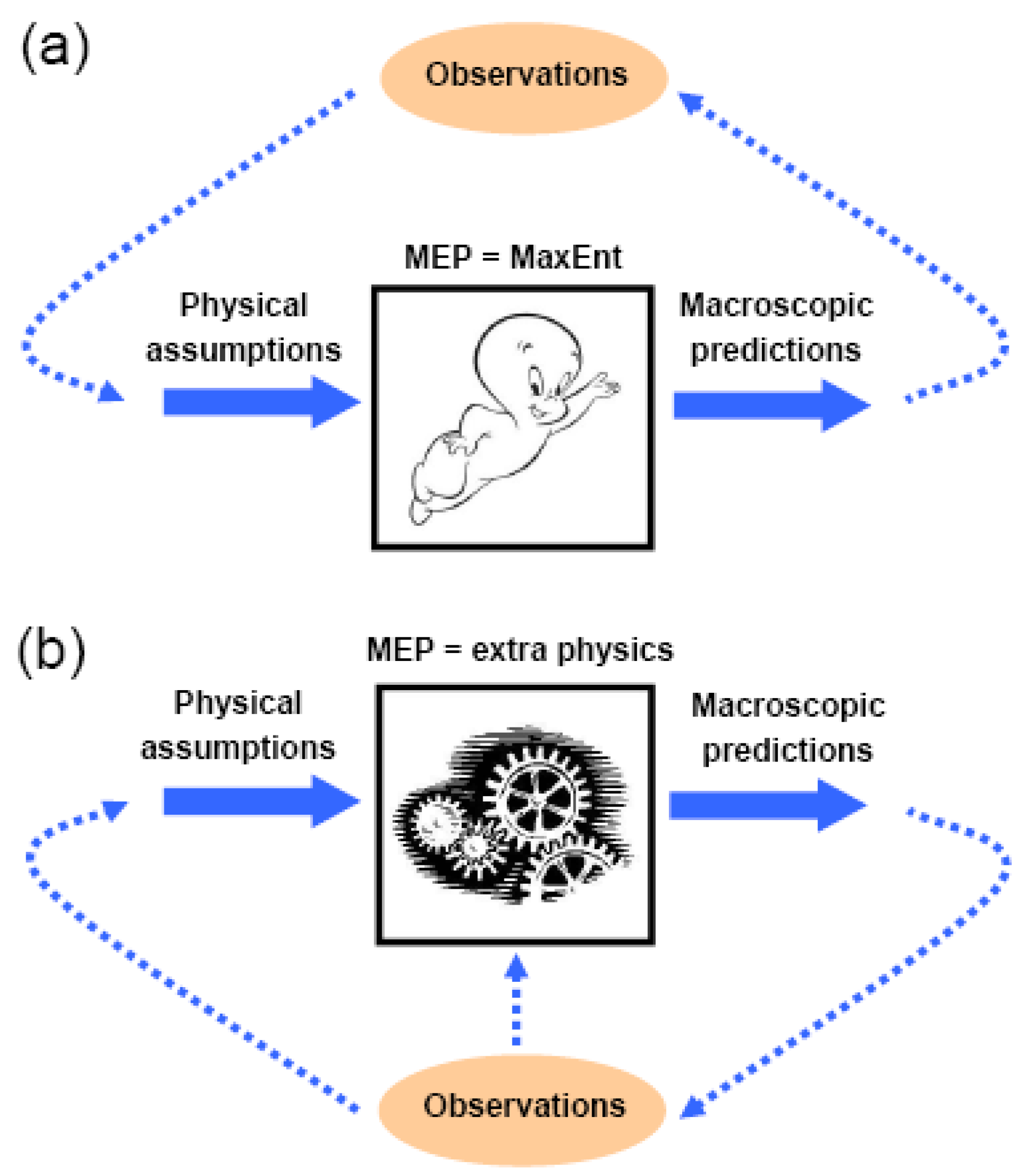
2. MaxEnt as Messenger of Essential Physics
2.1. The problem of macroscopic prediction
2.2. MaxEnt: an inference algorithm with no physical content
2.3. Does MaxEnt require N to be large?
 ) vs. experimental (
) vs. experimental (  ) probability distributions p(x) of some macroscopic observable x. N = number of microscopic degrees of freedom. Disagreement between the predicted and observed p(x) signals either (a) erroneous or (b) incomplete physics. Agreement between predicted and observed p(x) reveals the essential physics governing the statistical behaviour of x, whether that behaviour (c) is sharply-peaked about the mean or (d) involves large fluctuations. MaxEnt remains practically useful whether N is large or small.
) probability distributions p(x) of some macroscopic observable x. N = number of microscopic degrees of freedom. Disagreement between the predicted and observed p(x) signals either (a) erroneous or (b) incomplete physics. Agreement between predicted and observed p(x) reveals the essential physics governing the statistical behaviour of x, whether that behaviour (c) is sharply-peaked about the mean or (d) involves large fluctuations. MaxEnt remains practically useful whether N is large or small.
 ) vs. experimental (
) vs. experimental (  ) probability distributions p(x) of some macroscopic observable x. N = number of microscopic degrees of freedom. Disagreement between the predicted and observed p(x) signals either (a) erroneous or (b) incomplete physics. Agreement between predicted and observed p(x) reveals the essential physics governing the statistical behaviour of x, whether that behaviour (c) is sharply-peaked about the mean or (d) involves large fluctuations. MaxEnt remains practically useful whether N is large or small.
) probability distributions p(x) of some macroscopic observable x. N = number of microscopic degrees of freedom. Disagreement between the predicted and observed p(x) signals either (a) erroneous or (b) incomplete physics. Agreement between predicted and observed p(x) reveals the essential physics governing the statistical behaviour of x, whether that behaviour (c) is sharply-peaked about the mean or (d) involves large fluctuations. MaxEnt remains practically useful whether N is large or small.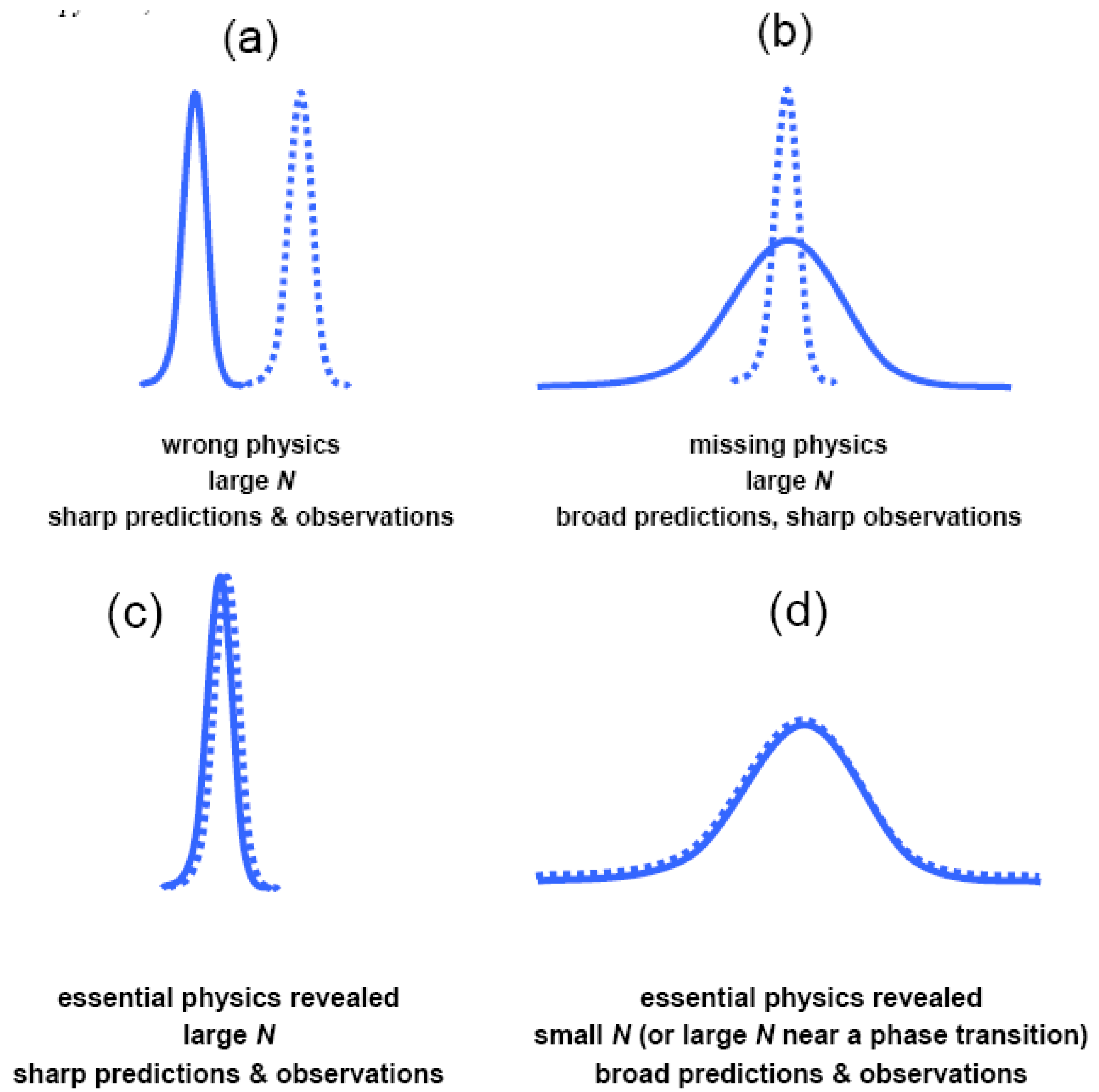
3. Implications of MaxEnt for MEP
3.1. Is MEP equivalent to MaxEnt?
3.2. What if the sea were made of vinegar?
3.3. MEP and the Upper Bound Theory of fluid turbulence
“The challenge therefore remains to find a [universal] functional whose optimization over a tractably reduced set of dynamical constraints leads to the emergence of realistic optimal velocity fields. Unfortunately, it remains unclear how to construct such a functional beyond intelligent guessing”.
3.4. So what?
4. Conclusions
Acknowledgements
References and Notes
- Ozawa, H.; Ohmura, A.; Lorenz, R.D.; Pujol, T. The second law of thermodynamics and the global climate system: A review of the maximum entropy production principle. Rev. Geophys. 2003, 41, 1018–1042. [Google Scholar] [CrossRef]
- Dewar, R.C. Information theory explanation of the fluctuation theorem, maximum entropy production and self-organized criticality in non-equilibrium stationary states. J. Phys. A: Math. Gen. 2003, 36, 631–641. [Google Scholar] [CrossRef]
- Dewar, R.C. Maximum entropy production and the fluctuation theorem. J. Phys. A: Math. Gen. 2005, 38, L371–L381. [Google Scholar] [CrossRef]
- Martyushev, L.M.; Seleznev, V.D. Maximum entropy production principle in physics, chemistry and biology. Phys. Rep. 2006, 426, 1–45. [Google Scholar] [CrossRef]
- Bruers, S. A discussion on maximum entropy production and information theory. J. Phys. A: Math. Theor. 2007, 40, 7441–7450. [Google Scholar] [CrossRef]
- Grinstein, G.; Linsker, R. Comments on a derivation and application of the “maximum entropy production” principle. J. Phys. A: Math. Theor. 2007, 40, 9717–9720. [Google Scholar] [CrossRef]
- Kleidon, A. Nonequilibrium thermodynamics and maximum entropy production in the Earth system. Naturwissenschaften 2009, 96, 653–677. [Google Scholar] [CrossRef] [PubMed]
- Caticha [From Inference to Physics, arXiv:0808.1260, 2008] has suggested that Newtonian mechanics itself is open to a statistical mechanical interpretation. This suggestion highlights the fact that in statistical mechanics what one considers to be a macroscopic phenomenon depends on the scale of the problem. Only by historical accident was the “mechanics” in statistical mechanics first taken to be Newtonian; the statistical interpretation of Newtonian mechanics itself as a macroscopic phenomenon posits a “sub-Newtonian mechanics” at even smaller scales. But none of this alters the point (to be made in the following paragraph) that, in any given problem, statistical mechanics distinguishes between the physical information that is given or assumed (both the macroscopic constraints and the assumed microscopic mechanics) and the statistical algorithm (MaxEnt) used to make macroscopic predictions from it.
- Longair, M.S. Theoretical Concepts in Physics; Cambridge University Press: Cambridge, UK, 1984; pp. 188–225. [Google Scholar]
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information theory and statistical mechanics. II. Phys. Rev. 1957, 108, 171–190. [Google Scholar] [CrossRef]
- Jaynes, E.T. Probability Theory: The Logic of Science; Bretthorst, G.L., Ed.; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Wu, N. The Maximum Entropy Method; Springer: Berlin, Germany, 1997. [Google Scholar]
- Essex, C.; Ilie, S.; Corless, R.M. Broken symmetry and long-term forecasting. J. Geophys. Res. 2007, 112, 1–9. [Google Scholar] [CrossRef]
- Dewar, R.C.; Porté, A. Statistical mechanics unifies different ecological patterns. J. Theor. Biol. 2008, 251, 389–403. [Google Scholar] [CrossRef] [PubMed]
- Niven, R.K. Origins of the combinatorial basis of entropy. In MaxEnt07; Knuth, K.H., Caticha, A., Center, J.L., Giffon, A., Rodriguez, C.C., Eds.; AIP: Melville, NY, USA, 2007; pp. 133–142. [Google Scholar]
- Boltzmann, L. Lectures on Gas Theory; Dover: New York, NY, USA, 1995. [Google Scholar]
- Gibbs, J.W. (1902); Elementary Principles of Statistical Mechanics; Reprinted by Ox Bow Press: Woodridge, CT, USA, 1981. [Google Scholar]
- Niven, R.K. Exact Maxwell-Boltzmann, Bose-Einstein and Fermi-Dirac statistics. Phys. Lett. A 2005, 342, 286–293. [Google Scholar] [CrossRef]
- Niven, R.K.; Grendar, M. Generalized classical, quantum and intermediate statistics and the Polya urn model. Phys. Lett. 2009, 373, 621–626. [Google Scholar] [CrossRef]
- Amit, D.J.; Martin-Mayer, V. Field Theory, The Renormalization Group, and Critical Phenomena, 3rd ed.; World Scientific Publishing: Singapore, 2005. [Google Scholar]
- Wang, G.M.; Sevick, E.M.; Mittag, E.; Searles, D.J.; Evans, D.J. Experimental demonstration of violations of the second law of thermodynamics for small systems and short time scales. Phys. Rev. Lett. 2002, 89, 050601. [Google Scholar] [CrossRef] [PubMed]
- Evans, D.J.; Searles, D.J. The fluctuation theorem. Adv. Phys. 2002, 51, 1529–1585. [Google Scholar] [CrossRef]
- Ziegler, H. An Introduction to Thermomechanics; North-Holland: Amsterdam, The Netherlands, 1983. [Google Scholar]
- Niven, R.K. Steady state of a dissipative flow-controlled system and the maximum entropy production principle. Phys. Rev. E 2009, 80, 021113:1–021113:15. [Google Scholar] [CrossRef]
- Dewar, R.C.; Maritan, A. Work in progress. 2009.
- Paltridge, G.W. The steady-state format of global climate. Quart. J. R. Met. Soc. 1978, 104, 927–945. [Google Scholar] [CrossRef]
- Rodgers, C.D. Comments on Paltridge’s “Minimum entropy exchange principle”. Quart. J. R. Met. Soc. 1976, 102, 455–457. [Google Scholar]
- Paltridge, G.W.; Farquhar, G.D.; Cuntz, M. Maximum entropy production, cloud feedback, and climate change. Geophys. Res. Lett. 2007, 34, L14708. [Google Scholar] [CrossRef]
- Lorenz, R.D.; Lunine, J.I.; Withers, P.G.; McKay, C.P. Titan, Mars and Earth: Entropy production by latitudinal heat transport. Geophys. Res. Lett. 2001, 28, 415–418. [Google Scholar] [CrossRef]
- Kerswell, R.R. Upper bounds on general dissipation functionals in turbulent shear flows: revisiting the “efficiency” functional. J. Fluid. Mech. 2002, 461, 239–275. [Google Scholar] [CrossRef]
- Ozawa, H.; Shimokawa, S.; Sakuma, H. Thermodynamics of fluid turbulence: A unified approach to the maximum transport properties. Phys. Rev. E. 2001, 64, 026303. [Google Scholar] [CrossRef]
- Malkus, W.V.R. Statistical stability criteria for turbulent flow. Phys. Fluids 1996, 8, 1582–1587. [Google Scholar] [CrossRef]
- Malkus, W.V.R. Borders of disorder: in turbulent channel flow. J. Fluid Mech. 2003, 489, 185–198. [Google Scholar] [CrossRef]
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Dewar, R.C. Maximum Entropy Production as an Inference Algorithm that Translates Physical Assumptions into Macroscopic Predictions: Don’t Shoot the Messenger. Entropy 2009, 11, 931-944. https://doi.org/10.3390/e11040931
Dewar RC. Maximum Entropy Production as an Inference Algorithm that Translates Physical Assumptions into Macroscopic Predictions: Don’t Shoot the Messenger. Entropy. 2009; 11(4):931-944. https://doi.org/10.3390/e11040931
Chicago/Turabian StyleDewar, Roderick C. 2009. "Maximum Entropy Production as an Inference Algorithm that Translates Physical Assumptions into Macroscopic Predictions: Don’t Shoot the Messenger" Entropy 11, no. 4: 931-944. https://doi.org/10.3390/e11040931



