Maximum Entropy Estimation of Transition Probabilities of Reversible Markov Chains
Abstract
:1. Introduction
2. Notation
3. Example: The 2-state Markov Chain
4. General Theory
5. Thermodynamics
5.1. Curved exponential family
5.2. Example: the 2-state Markov chain
5.3. Boltzmann-Gibbs distribution
6. Example: The 3-state Markov Chain
6.1. Potts model
6.2. Blume-Emery-Griffiths model
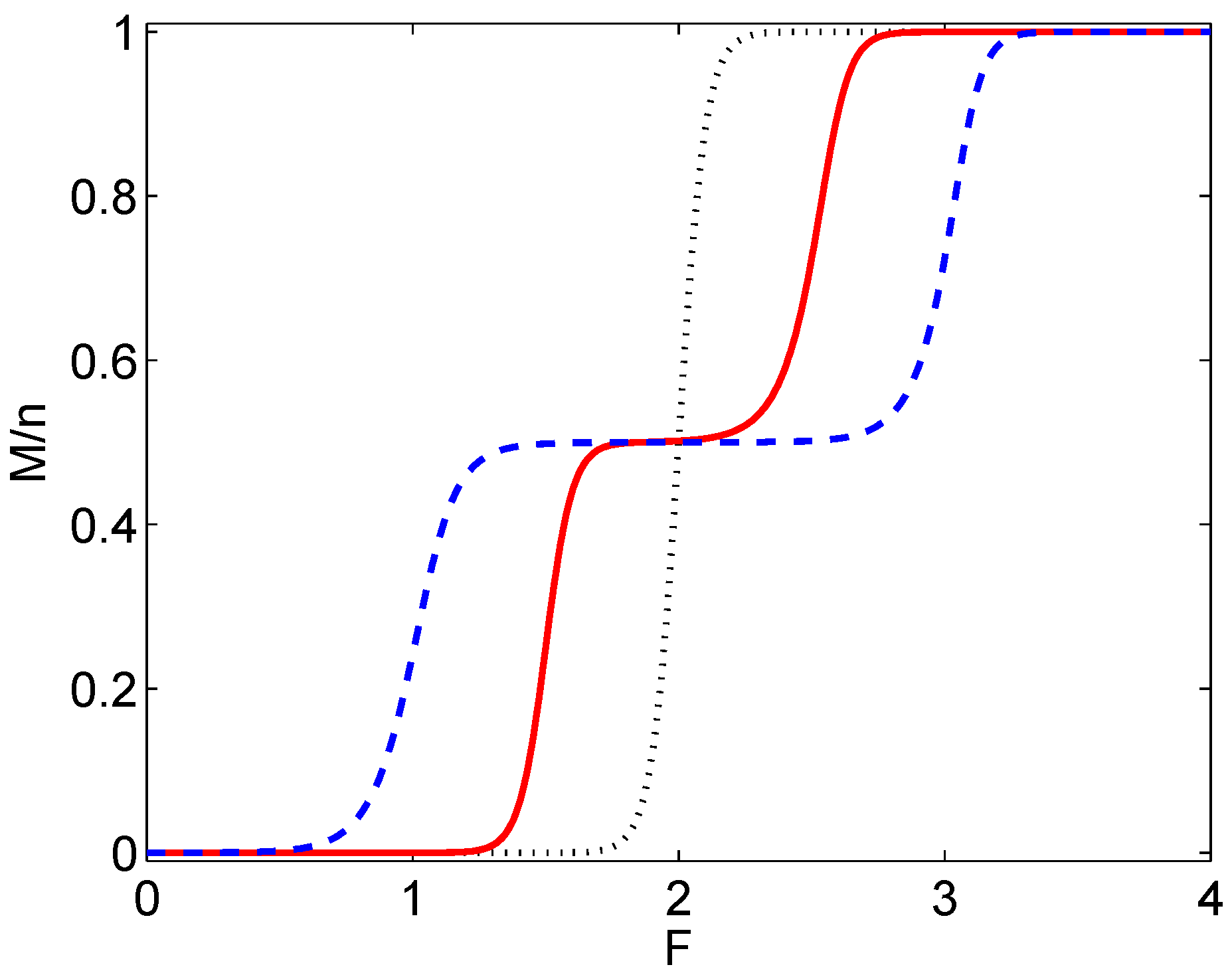
7. Discussion
Acknowledgements
Appendix
Appendix 1
Appendix 2
Appendix 3
References
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information theory and statistical mechanics II. Phys. Rev. 1957, 108, 171–190. [Google Scholar] [CrossRef]
- Rosenkrantz, R.D. Jaynes: Papers on Probability, Statistics and Statistical Physics; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1989. [Google Scholar]
- Callen, H.B. Thermodynamics and an Introduction to Thermostatistics; Wiley: New York, NY, USA, 1985. [Google Scholar]
- Van der Straeten, E.; Naudts, J. A one-dimensional model for theoretical analysis of single molecule experiments. J. Phys. A-Math. Theor. 2006, 39, 5715–5726. [Google Scholar] [CrossRef]
- Van der Straeten, E.; Naudts, J. Residual entropy in a model for the unfolding of single polymer chains. Europhys. Lett. 2008, 81, 28007:1–28007:5. [Google Scholar] [CrossRef]
- Van der Straeten, E.; Naudts, J. The 3-dimensional random walk with applications to overstretched DNA and the protein titin. Physica A 2008, 387, 6790–6800. [Google Scholar] [CrossRef]
- Van Campenhout, J.M.; Cover, T.M. Maximum entropy and conditional probability. IEEE Trans. Inf. Theor. 1981, IT-27, 483–489. [Google Scholar] [CrossRef]
- Csiszár, I.; Cover, T.M.; Choi, B.S. Conditional limit theorems under Markov conditioning. IEEE Trans. Inf. Theor. 1987, IT-33, 788–801. [Google Scholar] [CrossRef]
- Toda, M.; Kubo, R.; Saitô, N. Statistical Physics I: Equilibrium Statistical Mechanics; Springer-Verlag: Berlin, Germany, 1983. [Google Scholar]
- Wu, F.Y. The potts model. Rev. Mod. Phys. 1982, 54, 235–268. [Google Scholar] [CrossRef]
- Kassan-Ogly, F.A. One-dimensional 3-state and 4-state standard potts models in magnetic field. Phase Transit. 2000, 71, 39–55. [Google Scholar] [CrossRef]
- Blume, M.; Emery, V.J.; Griffiths, R.B. Ising model for the λ transition and phase separation in He3-He4 mixtures. Phys. Rev. A 1971, 4, 1071–1077. [Google Scholar] [CrossRef]
- Mancini, F.; Mancini, F.P. Magnetic and thermal properties of a one-dimensional spin-1 model. Condens. Matter Phys. 2008, 11, 543–553. [Google Scholar] [CrossRef]
- Naudts, J.; Van der Straeten, E. Transition records of stationary Markov chains. Phys. Rev. E 2006, 74, 040103:1–040103:4. [Google Scholar] [CrossRef]
- Kelly, F.P. Reversibility and Stochastic Networks; Wiley: Chichester, UK, 1979. [Google Scholar]
- Cornfeld, I.P.; Fomin, S.V.; Sinai, Y.G. Ergodic Theory; Springer-Verlag: New York, NY, USA, 1982. [Google Scholar]
- Gaspard, P. Time-reversed dynamical entropy and irreversibility in Markovian random processes. J. Stat. Phys. 2004, 117, 599–615. [Google Scholar] [CrossRef]
- Van der Straeten, E.; Naudts, J. A two-parameter random walk with approximate exponential probability distribution. J. Phys. A-Math. Theor. 2006, 39, 7245–7256. [Google Scholar] [CrossRef]
- Csiszár, I.; Shields, P.C. The consistency of the BIC Markov order estimator. Ann. Stat. 2000, 28, 1601–1619. [Google Scholar]
- Csiszár, I. Large-scale typicality of Markov sample paths and consistency of MDL order estimators. IEEE Trans. Inf. Theor. 2002, 48, 1616–1628. [Google Scholar] [CrossRef]
- Waterman, M.S. Introduction to Computational Biology; Chapman & Hall/CRC: Boca Raton, FL, USA, 1995. [Google Scholar]
- Schbath, S. An overview on the distribution of word counts in Markov chains. J. Comput. Biol. 2000, 7, 193–201. [Google Scholar] [CrossRef] [PubMed]
- Sage, A.P.; Melsa, J.L. Estimation Theory with Applications to Communications and Control; Mc-Graw-Hill: New York, NY, USA, 1971. [Google Scholar]
- Naudts, J. Parameter estimation in nonextensive thermostatistics. Physica A 2006, 365, 42–49. [Google Scholar] [CrossRef]
- Murray, M.K.; Rice, J.W. Differential Geometry and Statistics; Chapman & Hall: London, UK, 1993. [Google Scholar]
- Naudts, J. Generalised exponential families and associated entropy functions. Entropy 2008, 10, 131–149. [Google Scholar] [CrossRef]
- Naudts, J. The q-exponential family in statistical physics. Cent. Eur. J. Phys. 2009, 7, 405–413. [Google Scholar] [CrossRef]
- Chen, X.Y.; Jiang, Q.; Shen, W.Z.; Zhong, C.G. The properties of one-dimensional spin-S (S≥1) antiferromagnetic Ising chain with single-ion anisotropy. J. Magn. Magn. Mater. 2003, 262, 258–263. [Google Scholar] [CrossRef]
- Van der Straeten, E.; Naudts, J. The globule-coil transition in a mean field approach. arXiv:cond-mat/0612256 2006. [Google Scholar]
© 2009 by the author; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license http://creativecommons.org/licenses/by/3.0/.
Share and Cite
Van der Straeten, E. Maximum Entropy Estimation of Transition Probabilities of Reversible Markov Chains. Entropy 2009, 11, 867-887. https://doi.org/10.3390/e11040867
Van der Straeten E. Maximum Entropy Estimation of Transition Probabilities of Reversible Markov Chains. Entropy. 2009; 11(4):867-887. https://doi.org/10.3390/e11040867
Chicago/Turabian StyleVan der Straeten, Erik. 2009. "Maximum Entropy Estimation of Transition Probabilities of Reversible Markov Chains" Entropy 11, no. 4: 867-887. https://doi.org/10.3390/e11040867



