1. Introduction
Since C. Shannon published his famous paper “A mathematical theory of communication” [
1] the fundamental role of information theory has been appreciated not only in its direct applications, but also in robotics, linguistics and biology.
The communication systems and related cognitive skills of animals are a matter of special interest to ethologists, psychologists, linguists, and specialists in artificial intelligence and robotics. Attempts to approach the question whether highly social and intelligent species can exchange meaningful messages are based on a natural idea that the complexity of communication should be connected with high levels of sociality, cognition and cooperation in animals’ societies [
2]. In the 1960s and 1970s, elegant but ambiguous experiments were conducted in which animals were asked to pass some pieces of information to each other. In Menzel’s [
3] experiments, a group of chimpanzees living in an enclosure searched for hidden food. Menzel suggested that chimpanzees possess means for transferring information about both location and properties of objects, but it remained unclear how they did this. In other experiments the cooperative behavior of dolphins was investigated, which could involve intelligent communication. To get a fish, two dolphins, separated by an opaque barrier, had to press the paddles in the correct order. The obtained results enabled researchers to suggest that the dolphins can co-ordinate the actions of each other, probably, by means of acoustic signals [
4]. Despite these supportive experiments that demonstrated that members of highly social intelligent species really have what to “say” to each other, the question of existence of developed “languages” in non-human beings remained so far obscure.
The main difficulties in the analysis of animal “languages” appear to be methodological. Many researchers have tried to directly decipher animal language by looking for “letters” and “words” and by compiling “dictionaries” [
5], for a review see [
6]. However, only two cases of natural communications have been decoded up to the present. First, one of the most complicated of the known natural “languages” in animals is the symbolic honey bee “Dance language”. Discovered by K. Von Frisch [
7,
8] it was later intensively studied using different methods including robotics and radars [
9,
10]. The second case of a successful deciphering of several natural signals concerned alarm calls in vervet monkeys which appeared to give different alarm calls to eagles, snakes and leopards [
11]. Later “semantic” alarm calls and food calls were described for several other species [
12,
13]; for a detailed review see [
6]. The fact that researchers have managed to compile such “dictionaries” for a few species only, appears to indicate not that other animals lack “languages”, but that adequate methods are lacking. In both cases of communications that became partly accessible for investigators, expressive and distinctive signals correspond to repeatable and frequently occurring situations in the context of animals’ life, and thus can serve as “keys” for decoding their signals.
The problem of cracking animals’ codes have become especially attractive since the great “linguistic” potential was discovered in several highly social and intelligent species by means of intermediary artificial languages. Being applied to apes, dolphins and grey parrots, this method has revealed astonishing mental skills in the subjects [
14,
15,
16,
17]. It is become possible to demonstrate that animals are capable not only of decision making and using the experience gained in new situations, but also of using simple grammatical rules, visual symbols and number-related skills. For example, language-trained chimpanzees were found to be able to add and subtract small numbers [
18]—the ability that was not available for discovery without the use of intermediary languages.
However, it is important to note that this way to communicate with animals is based on adopted human languages. Yet surprisingly little is known about natural communication systems of those species that were involved in language-training experiments. Explorers of animal language behavior thus have met a complex problem of resolving the contradiction between their knowledge about significant “linguistic” and cognitive potential in some species and limitations in cracking their natural codes [
19].
We have suggested a principally new experimental paradigm based on concepts of Information Theory [
20,
21,
22]. The main point of our approach is not to decipher signals but to investigate the very process of information transmission by measuring time duration which the animals spend on transmitting messages of definite lengths and complexities. Being applied to studying communication in highly social ant species, this approach enabled us to reveal basic properties of ant “language” and estimate their cognitive skills.
Ants are good candidates for studying general rules of natural communication and cognition, because these insects are known to combine highly integrative colony organization with sophisticated cognitive skills. Ants possess complex forms of communications, and they are known to be able to use a large variety of communication means for attracting their nestmates to a food source [
23]. It has remained unclear for a long time whether ants can use distant homing (distant homing here is a term used in social insects studies which means that messages about remote events come from the scouting individual, without other cues such as scent trail or direct guiding; for reviews see [
6,
23].) In this aspect, the so-called tactile (or antennal) “code” has been discussed since 1899, when it was first hypothesized such an information transmission system in ants [
24]. Although the numerous attempts to decipher ants’ “tactile language” have not given the desired results (for a review see [
25]) we are disposed to consider “antennal code” the essential component of ants’ “language”. At the same time, it is clear that highly social ant species possess the necessary prerequisites for complex communication. Experimental studies revealed sophisticated forms of social learning in ants [
26]. However, methodological limitations have hampered the progress of studying “linguistic potential” of ants’ communication, and the problem of distant homing in these insects has not been solved before our experiments.
The experimental paradigm of our approach is simple. All we need to do is to establish a situation where ants must transfer a specific amount of information to each other. The crucial idea of the first scheme of experiments is that we know exactly the quantity of information to be transferred. To organize the process of information transmission between ants, a special maze has been used, called a “binary tree” [
21], where the number and sequence of turns towards the goal corresponds to the amount of the information to be transferred. In another series of experiments ants had to transfer the information about the number of a branch in comb-like “counting mazes”.
It has been firstly demonstrated that group-retrieving Formica species possess distant homing, and they are able to pass meaningful messages. We also succeeded in studying important properties of ants’ cognitive capacities, namely their ability to grasp regularities, to use them for coding and “compression” of information, and to add and subtract small numbers to optimize their messages.
The obtained results demonstrate what Information Theory can furnish for explorers of communication and intelligence in social animals. This new experimental paradigm provides a way for studying important characteristics of animal communication which have not been accessible for study before, such as the rate of information transmission and the potential flexibility of communication systems. We also succeeded in studying some important properties of ants’ intelligence, namely, their ability to grasp regularities and use them for optimization their messages.
2. Using Shannon Entropy and Kolmogorov Complexity to Study Communicative System in Ants: The Binary Tree Experiments
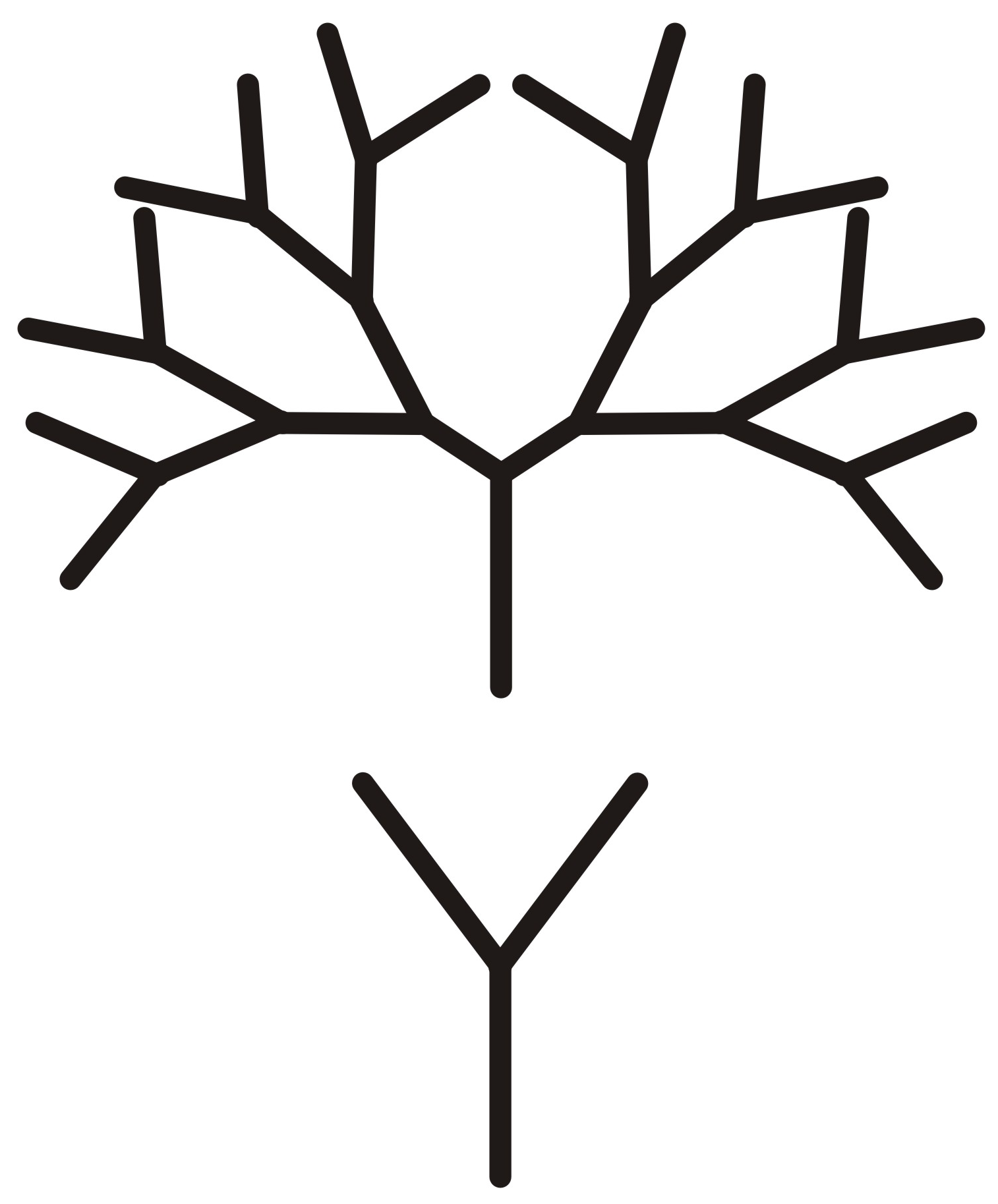
The experiments based on Shannon entropy present a situation in which, in order to obtain food, ants have to transmit certain information which is quantitatively known to the researcher. This information concerns the sequence of turns towards a trough with syrup. The laboratory maze “binary tree” is used where each “leaf” of the tree ends with an empty trough with the exception of one filled with syrup. The leaf on which to place the filled trough was chosen randomly by tossing a coin for each fork in the path. The simplest design is a tree with one fork and two leaves, that is, a Y-shaped maze. It represents one binary choice which corresponds to one bit of information. In this situation a scouting animal should transmit one bit of information to other individuals: to go to the right (R) or to the left (L) (see
Figure 1). In other experiments the number of forks of the binary tree increased to six. Hence, the number of bits necessary to choose the correct way is equal to the number of forks, that is, turns to be taken (
Figure 2 shows a labyrinth with 3 forks).
The use of ideas of Shannon Entropy allowed the presence of potentially unlimited numbers of messages in ant “language” to be demonstrated and estimates of the rate of information transmission (approximately 1 bit/min) to be made. We also succeeded in studying some properties of ants’ intelligence, namely, their ability to memorize and to use simple regularities, thus compressing the information available. The latter experiments were based on the ideas of Kolmogorov complexity.
2.1. The experimental scheme
Figure 1.
The maze “binary tree” with one fork and four forks.
Figure 1.
The maze “binary tree” with one fork and four forks.
In the “binary tree” experiments ants were confronted with a rather complex life-or-death task: they could obtain food only in a “binary tree” maze and only once every 2–3 days. Ants therefore were hungry and extremely motivated to obtain some food. They had to search for the food placed on one of leaves of the “binary tree” maze (
Figure 1 and
Figure 2). During different years three colonies of
Formica polyctena and two of
F. sanguinea were used. Ants lived in the
-meters laboratory arena, in a transparent nest that made it possible for their activity to be observed. The arena was divided into two sections: a smaller one containing the nest, and a bigger one with an experimental system (
Figure 2). The two sections were connected by a plastic bridge that was removed from time to time to modify the set-up or to isolate the ants. To prevent access to the food in the maze by a straight path, the set-up was placed in a bath of water, and the ants reached the initial point of the binary tree by going over a second small bridge.
The laboratory colonies consisted of about 2,000 individuals each. All actively foraging ants were individually marked with colored paint. The laboratory colonies were found to include teams of constant membership which consisted of one scout and three to eight recruits (foragers): the scout mobilized only members of its team to the food. The composition of the teams was revealed during special run-up experiments consisting of familiarization trials lasting as long as two or three weeks (see details in [
25]). In total, 335 scouts along with their teams were used in all experiments with the binary tree. In each trial one of the scouts that were actively moving on the experimental arena at that moment was placed on a leaf of the binary tree that contained a trough with the food, and then it returned to the nest by itself. All contacts between the scout and its team were observed and time duration was recorded each time.
Figure 2.
The laboratory arena with the maze “binary tree”.
Figure 2.
The laboratory arena with the maze “binary tree”.
All experiments were so devised as to eliminate all possible cues that could help the ants to find the food, except information contact with the scout. To avoid the use of an odor track, the experimental set-up was replaced by an identical one when the scout was in the nest or on the arena contacting its group. All troughs in the fresh maze contained only water to avoid the possible influence of the smell of syrup. If the group reached the correct leaf of the binary tree, they were immediately presented with the food. The scout had to make up to four trips before it was able to mobilize its group of foragers. Usually members of the team had already left the nest after the scout’s first trip and were waiting on the arena for its return. Returning to the group, the scout contacted one to four foragers in turn, sometimes two of them simultaneously. Contacts were followed by numerous antennal movements. The experiments were designed to investigate the characteristics of distant homing, so after the scout had contacted its team, it was isolated for a while, and the foragers had to search for the food by themselves. This process will be described in more details in the next section. Here it is important to note that the composition of the working teams remained constant in each colony from several days to several weeks, that is, during periods when a given scout was actively working (see detailed tables in [
21]). It is notable that in both
F. polyctena and
F. sanguinea, not all of the scouts managed to memorize the way to the correct leaf of the maze even after they had passed their “final exams” during the run-up trials. The number of scouts that succeeded in memorizing the way decreased with increasing complexity of the task. In the case of two forks all active scouts and their groups (up to 15 per colony) were successful whereas in the case of six forks, only one or two coped with the task.
During the experiments each scout was placed on the trough containing food, and after the scout had eaten it returned to the nest on its own. In all cases of mobilization of the group the duration of the contact between the scout and the foragers was measured in seconds. The contact was considered to begin when the scout touched the first forager ant, and to end when the first two foragers left the nest for the maze. When the scout repeatedly returned to the trough alone, each of its contacts with foragers was measured. Only the duration of the contact that was followed by the foragers’ leaving the nest was taken into account. These contacts were hypothesized to be “informative”, and they differed sharply in duration from other contacts: all were more than 30 seconds. As a rule, all of the previous contacts between scouts and foragers were brief (about 5 seconds) and were made for the exchange of food. During each series of experiments with the trough placed on the th leaf of the binary tree, all teams that were active on that day worked successively. While the trial was going on, the bridge leading to the working part of the arena was taken away, so as not to let members of other teams to go there. While the scout was inside the nest, the whole maze was replaced by a fresh one with all troughs empty. Foragers were presented with the syrup if they reached the correct leaf of the binary tree.
2.2. Information transmission by distant homing in ants: statistical proof
Before analyzing ants’ “linguistic potential” and their ability to use rules for compression of information we consider the evidence of information transmission from the scouts to the foragers, which came from two sets of data: first, from statistical analysis of the number of faultless findings of the goal by a group, and second, from a special series of control experiments with “uninformed” (“naive”) and “informed” foragers. The statistical analysis of the number of faultless findings of the goal was carried out by comparing the hypothesis
(ants find the leaf containing the food by chance) with the hypothesis
(they find the goal thanks to the information obtained), proceeding from the fact that the probability of finding the correct way by chance when the number of forks is
i is
. We analyzed different series of experiments (338 trials in sum), separately for 2, 3, 4, 5, and 6 forks. In all cases
was rejected in favor of
(see [
22]), thus unambiguously demonstrating information transmission from scouts to foragers.
The control experiments were organized so as to compare searching results of the ants that had and had not previous possibility to contact the scout (the “informed” and “naive” ants, respectively). The “naive” and “informed” ants were tested one by one. Each ant was allowed to search for the food for 30 minutes. In
Table 1 the time spent on searching the trough by “informed” and “uninformed”
Formica pratensis are compared [
27,
29]. For every trial, Wilcoxon’s non-parametric test was used [
30] to test the hypothesis
(data from both samples follow the same distribution) against
(they follow different distributions) at significance level
. We concluded that the duration of searching time is essentially smaller in those ants that had previously contacted the scout. These data demonstrate that scouts transfer information about the discovered food to foragers by means of distant homing.
Table 1.
Comparison of duration of searching the trough by “uninformed” (U) F. pratensis ants and individuals that previously contacted with the successful scout (“informed”, I).
Table 1.
Comparison of duration of searching the trough by “uninformed” (U) F. pratensis ants and individuals that previously contacted with the successful scout (“informed”, I).
| Sequence of the turns | Ants (U/I) | Mean (second) | Amounts of sampling | P |
| RRRR | U | 345.7 | 9 | <0.01 |
| | I | 36.3 | 9 | |
| LLLL | U | 508.0 | 9 | <0.01 |
| | I | 37.3 | 9 | |
| LRRL | U | 118.7 | 7 | <0.01 |
| | I | 16.6 | 7 | |
| RLLR | U | 565.9 | 7 | <0.01 |
| | I | 16.3 | 7 | |
2.3. The rate of information transmission in ants
We now can evaluate the rate of information transmission in ants. To do this, observe that the quantity of information (in bits) necessary to choose the correct route in the maze equals i, the depth of the tree (the number of turns to be taken), that is, where n is the number of leaves. One can assume that the duration of the contacts between the scouts and foragers (t) is , where i is the number of turns (the depth of the tree), a is the rate of information transmission (bits per minute), and b is an introduced constant, since ants can transmit information not related directly to the task, for example, the simple signal “food”. Besides, it is not ruled out that a scout ant transmits, in some way, the information on its route to the nest, using acoustic or some other means of communication. In this context, it is important to note that the route from the maze to the nest on the arena was in all experiments approximately the same, that is, the experimental setup was always placed on the same part of the working part of the arena. Being highly motivated, scouts hurried on to the nest in a beeline, and, therefore, the time before they made antennal contact with the foragers in the nest, which the scout could hypothetically use for message transmission, was approximately the same and did not depend on the number of turns to be taken in the maze.
From the data obtained, the parameters of linear regression and the sample correlation coefficient (r) can be evaluated. The rate of information transmission (a) derived from the equation was 0.738 bits per minute for F. sanguinea and 1.094 bits per minute for F. polyctena. The rate of information transmission is relatively small in ants.
To estimate the potential productivity of ants’ “language”, let us count the total number of different possible routes to the trough. In the simplest binary tree with one fork there are two leaves and therefore two different routes. In a tree with two forks there are routes, with three forks routes, and with six forks, routes; hence, the total number of different routes is at least . This is the number of messages the ants must be able to pass in order to pass the information about the food placed on any leaf of the binary tree with 6 forks.
2.4. The Kolmogorov complexity and data compression in the ants language
Another series of experiments with the binary tree was inspired by the concept of Kolmogorov complexity and was designed to check whether highly social ant species possess such an important property of intelligent communications as the ability to grasp regularities and to use them for encoding and “compressing” information. This concept is applied to words (or text) composed of the letters of any alphabet, for example, of an alphabet consisting of two letters: L and R. We interpret a word as a sequence of left (L) and right (R) turns in a maze. Informally the complexity of a word (and its uncertainty) equates to its most concise description, according to Kolmogorov [
31,
32]. For example, the word “LLLLLLLL” can be represented as “8 L”, the word “LRLRLRLR” as “4LR”, while the “random” word of shorter length “LRRLRL” probably cannot be expressed more concisely, and this is the most complex of the three.
We analyzed the question of whether ants can use simple regularities of a “word” to compress it. It is known that Kolmogorov complexity is not algorithmically computable. Therefore, strictly speaking, we can only check whether ants have a “notion” of simple and complex sequences. In our binary tree maze, in human perception, different routes have different complexities.
In one particular series of experiments, F. sanguinea ants were presented with different sequences of turns. We applied a statistical test in order to examine whether the time for transmission of information by ants depends on its complexity. We considered two hypotheses. The main hypothesis is , that is, the time for transmission of information does not depend on the complexity of the “text”. The alternative hypothesis is that this time actually depends on the complexity of the “text”. We rejected , thus showing that the more time ants spent on the information transmission, the more complex - in the sense of Kolmogorov complexity - was the message.
Let us test these hypotheses formally. There are seven sequences of turns of equal length (lines 5–8 and 13–15 at
Table 2). The total number of turn sequences orders, according to the duration of the transmission is
of which
are in the line with
. The probability of obtaining such an order according to
is very small:
. Thus, we accept the hypothesis
: the simpler the text the less time for information transmission.
It is interesting that the ants began to use regularities to compress only quite large “words”. Thus, they spent from 120 to 220 seconds to transmit information about random turn patterns on the maze with five and six forks and from 78 to 135 seconds when turn patterns were regular. On the other hand, there was no essential difference when the length of sequences was less than 4 (
Table 2).
These results enable us to suggest that ants not only produce a large number of messages but can use simple forms of rule extraction in order to optimize their messages, that is, to spend less time for transferring “regular” sequences of turns. The ability to grasp regularities and to use them for coding and “compression” of information can be considered as one of the most important properties of language and its carriers’ intellect.
Table 2.
Duration of transmitting information on the way to the trough by F.sanguinea scouts to foragers (no.1-8 regular turn pattern; no. 9–15 random turn pattern.)
Table 2.
Duration of transmitting information on the way to the trough by F.sanguinea scouts to foragers (no.1-8 regular turn pattern; no. 9–15 random turn pattern.)
| No | Sequence | Mean duration (sec) | Numbers of experiments |
| 1 | LL | 72 | 18 |
| 2 | RRR | 75 | 15 |
| 3 | LLLL | 84 | 9 |
| 4 | RRRRR | 78 | 10 |
| 5 | LLLLLL | 90 | 8 |
| 6 | RRRRRR | 88 | 5 |
| 7 | LRLRLR | 130 | 4 |
| 8 | RLRLRL | 135 | 8 |
| 9 | LLR | 69 | 12 |
| 10 | LRLL | 100 | 10 |
| 11 | RLLR | 120 | 6 |
| 12 | RRLRL | 150 | 8 |
| 13 | RLRRRL | 180 | 6 |
| 14 | RRLRRR | 220 | 7 |
| 15 | LRLLRL | 200 | 5 |
3. The Ants’ Numerical Competence
Basic number-related skills, that is, knowledge of quantities and their relations, is, perhaps, one of the highest properties of cognition. Recent studies have demonstrated some species as being able to judge about numbers of stimuli, including things, and sounds, and maybe smells. For example, lions can count roaring that comes from individuals who are not members of the pride [
33]; honey bees are able to use the number of landmarks as one of the criteria in searching for food sources [
34]. There are many other examples that come from different animal species, from mealy beetles [
35] to elephants [
36]; however, we are still lacking an adequate “language” for comparative analysis. The main difficulty in comparing numerical abilities in humans and other species is that our numerical competence is closely connected with abilities for language usage and for symbolic representation.
We elaborated an experimental paradigm for studying ants’ numerical competence [
28,
37]. A scouting ant has to transfer the information about a number (in our case, the index number of a branch of a maze) to its nest mates. Quantitative characteristics of the ants’ communications were used for investigating their ability to count. The main idea of this experimental paradigm is that experimenters can judge how ants represent numbers by estimating how much time individual ants spend on “pronouncing” numbers, that is, on transferring information about index numbers of branches.
3.1. The comb-like setups
The experiments were based on a procedure similar to the binary tree study. Ant scouts were required to transfer to foragers in a laboratory nest the information about which branch of a special “counting maze” they had to go to in order to obtain syrup. “Counting maze” is a collective name for several variants of set-ups. All of them serve to examine how ants transfer information about index numbers of branches by means of distant homing.
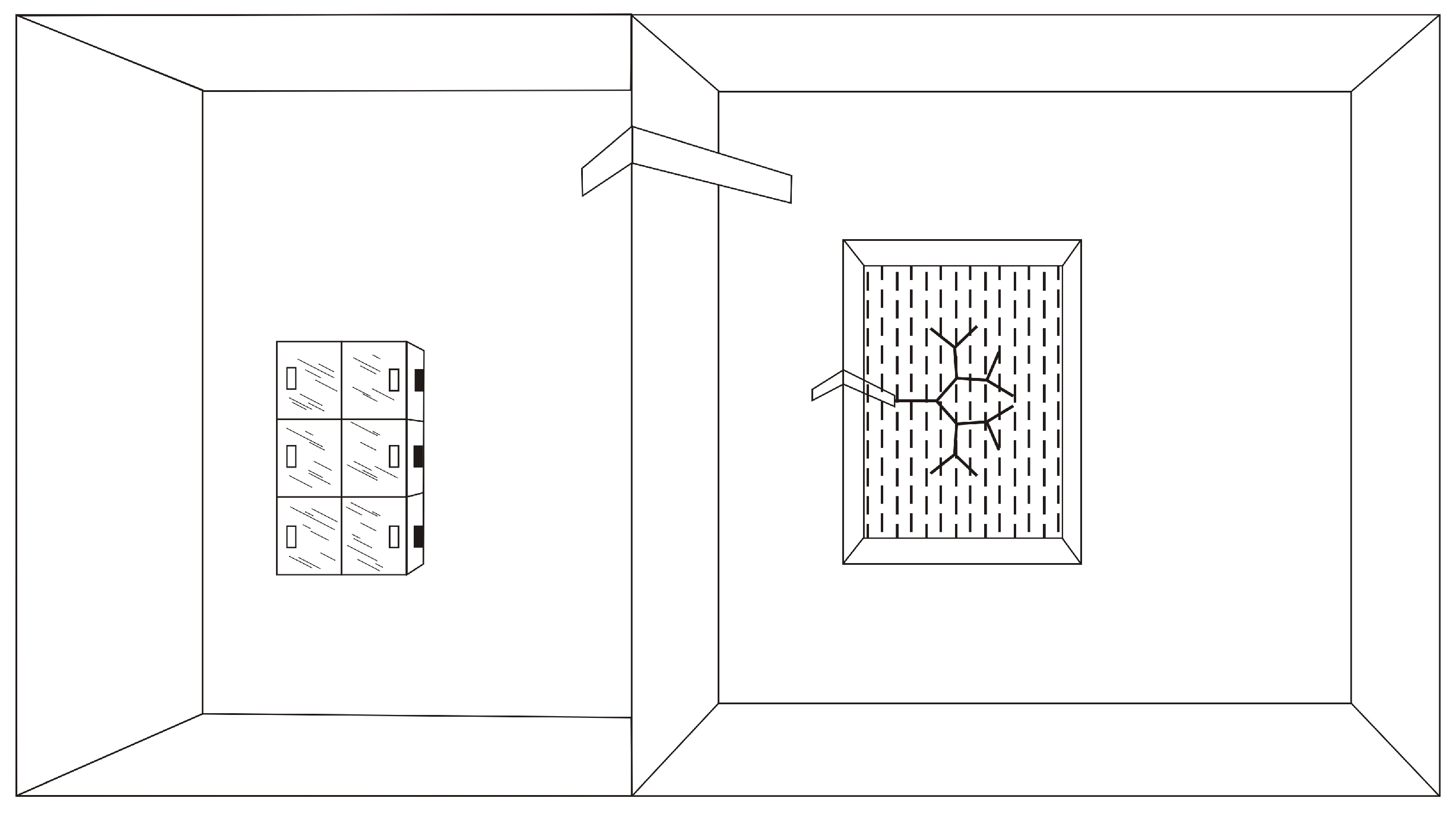
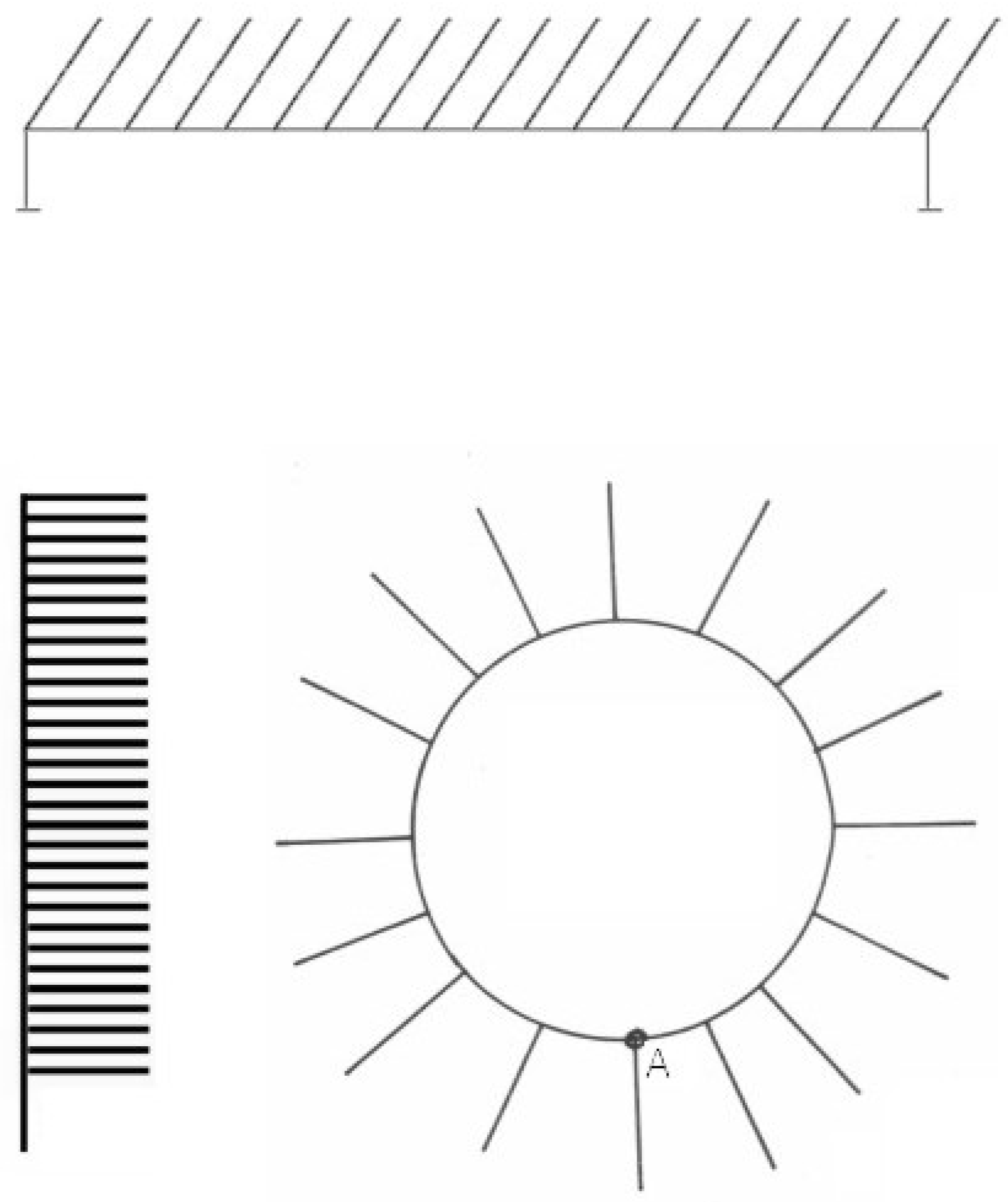
Figure 3.
The comb-like set-ups for studying numerical competence in ants: a horizontal trunk, a vertical trunk and a circle.
Figure 3.
The comb-like set-ups for studying numerical competence in ants: a horizontal trunk, a vertical trunk and a circle.
The first variant of the counting maze is a comb-like setup consisting of a long horizontal plastic trunk with 25 to 60 equally spaced plain plastic branches, each of them 6 cm in length (
Figure 3). Each branch ended with an empty trough, except for one filled with syrup. Ants came to the initial point of the trunk over a small bridge. The second variant is a set-up with vertically aligned branches. In order to test whether the time of transmission of information about the number of the branch depends on its length as well as on the distance between the branches, one set of experiments was carried out on a similar vertical trunk in which the distance between the branches was twice as large, and the branches themselves were three times and five times longer (for different series of trials). The third variant was a circular trunk with 25 cm long branches.
Similarly to the binary tree study, ants were housed in a laboratory arena divided into two parts, one containing a plastic nest with a laboratory ant colony and another containing one of the variants of the counting maze. During different years two laboratory colonies of F. polyctena were used in this set of experiments. Each series of experiments was preceded by the run-up stage consisting of familiarization trials. In order to force a scout to transfer the information about food to its nest mates we showed it the trough containing syrup (placing the scout directly on the trough) and then let it return to the nest. After allowing it to contact the foragers within the nest, the scout was removed and isolated for a while, so that the foragers had to search for the food by themselves, without their guide.
Again, similar to the binary tree study, the experiments with counting mazes were devised so as to eliminate all possible ways for the members of each foraging team to find a goal, except by distant homing, i.e., an information contact with their scout. The set-up was replaced with a fresh one, with all troughs filled with water, while the scout was in the nest; if the foraging team reached the correct branch in a body, then the water-filled trough was replaced with one with syrup; thus foragers had to rely solely on the information from the scout.
3.2. The ants’ ability to transfer the information about numbers of objects
The findings concerning number-related skills in ants are based on comparisons of duration of information contacts between scouts and foragers which preceded successful trips by the foraging teams. Duration of contacts of the scout with its team was measured when the scout returned from the experimental set-up, loaded with both syrup and information. In total, 32 scout-foragers teams worked in three kinds of set-ups. The teams left the nest after they were contacted by scouts and moved towards the trough by themselves 152 times (recall that the scouts were removed and the set-ups were replaced). In 117 cases the team immediately found the correct path to the trough, without making any wrong trips to empty troughs. In the remaining cases, ants came to the empty troughs, and began looking for food by checking neighboring branches.
Since all set-ups had no fewer than 25 branches, the probability of finding the correct trough by chance is not more than . Thus, the success ratio which was obtained experimentally can only be explained by information transmission from the scouts. The probability of finding the food-containing trough by chance in 117 cases out of 152 is less than . In addition, in control experiments ants, including scouts placed in the set-up, without information on which trough contained food usually failed to find the food, even though they actively searched for it.
Data obtained on the vertical trunk are shown in
Table 3 as an example. It turned out that the relation between the index number of the branch and the duration of the contact between the scout and the foragers is well described by the equation
for different set-ups which are characterized by different shapes, distances between the branches and lengths of the branches. The values of parameters
a and
b are close and do not depend either on the lengths of the branches or on other parameters. The correlation coefficient between
t and
i was high for different kinds of counting mazes; see
Table 4. All this enables us to suggest that the ants transmit information solely concerning the index number of the branch.
It is interesting that quantitative characteristics of the ants’ “number system” seem to be close, at least outwardly, to some archaic human languages: the length of the code of a given number is proportional to its value. For example, the word “finger” corresponds to 1, “finger, finger” to the number 2, “finger, finger, finger” to the number 3 and so on. In modern human languages the length of the code word of a number i is approximately proportional to (for large i’s), and the modern numeration system is the result of a long and complicated development.
Table 3.
The results of experiments in the “vertical trunk 1” with F. polyctena.
Table 3.
The results of experiments in the “vertical trunk 1” with F. polyctena.
| No | Number of food-containing branch | Duration of scout-forager contact (sec) | the scout’s “name” |
| 1 | 10 | 42 | I |
| 2 | 10 | 40 | II |
| 3 | 10 | 45 | III |
| 4 | 40 | 300 | II |
| 5 | 40 | 280 | IX |
| 6 | 13 | 90 | II |
| 7 | 13 | 98 | I |
| 8 | 28 | 110 | III |
| 9 | 28 | 120 | X |
| 10 | 20 | 120 | X |
| 11 | 20 | 110 | III |
| 12 | 35 | 260 | III |
| 13 | 35 | 250 | X |
| 14 | 30 | 160 | I |
| 15 | 30 | 170 | III |
Table 4.
Values of correlation coefficient (r) and regression () coefficients for vertical trunk (vert), horizontal trunk (horiz), and circle in the experiments with F. polyctena.
Table 4.
Values of correlation coefficient (r) and regression () coefficients for vertical trunk (vert), horizontal trunk (horiz), and circle in the experiments with F. polyctena.
| Type of setup | Sample size | Numbers of branches | r | a | b |
| Vert.1 | 15 | 40 | 0.93 | 7.3 | -28.9 |
| Vert.2 | 16 | 60 | 0.99 | 5.88 | -17.11 |
| Horiz.1 | 30 | 25 | 0.91 | 8.54 | -22.2 |
| Horiz.2 | 21 | 25 | 0.88 | 4.92 | -18.94 |
| Circle | 38 | 25 | 0.98 | 8.62 | -24.4 |
3.3. The ants’ ability to add and subtract small numbers
There are some experimental evidence that two years old human children, rhesus monkeys and chimpanzees can operate with addition and subtraction of up to 4. The experiments are based on games where subjects should demonstrate their abilities to judge about the number of items after the addition or removal [
38].
We elaborated a new experimental paradigm of studying ants’ “arithmetic” skills based on a fundamental idea of information theory, which is that in a “reasonable” communication system the frequency of usage of a message and its length must correlate. The informal pattern is quite simple: the more frequently a message is used in a language, the shorter is the word or the phrase coding it. This phenomenon is manifested in all known human languages.
The main experimental procedure was similar to other experiments with counting mazes. In various years four colonies of F. polyctena were used in this set of experiments. The scheme of the experiments was as follows. Ants were offered a horizontal trunk with 30 branches. The experiments were divided into three stages, and at each of them the regularity of placing the trough with syrup on branches with different numbers was changed. At the first stage, the branch containing the trough with syrup was selected randomly, with equal probabilities for all branches. So the probability of the trough with syrup being placed on a particular branch was . At the second stage we chose two “special” branches A and B (N 7 and N 14; N 10 and N 20; and N 10 and N 19 in different years) on which the trough with syrup occurred during the experiments much more frequently than on the rest—with a probability of for “A” and “B”, and for each of the other 28 branches. In this way, two “messages”—“the trough is on branch A” and “the trough is on branch B”—had a much higher probability than the remaining 28 messages. In one series of trials we used only one “special” point A (the branch N 15). On this branch the food appeared with the probability of , and for each of the other 29 branches. At the third stage of the experiment, the number of the branch with the trough was chosen at random again.
Now let us consider the relationship between the time which the ants spent to transmit the information about the branch containing food, and its number. The information obtained at the first and third stages of the experiments are shown on the graph (
Figure 4) in which the time of the scout’s contact with foragers
is plotted against the number
of the branch with the trough. At the first stage the dependence is close to linear. At the third stage, the picture was different: first, the information transmission time was very much reduced, and, second, the dependence of the information transmission time on the branch number is obviously non-linear: depression can be seen in the vicinities of the “special” points (10 and 20). So the data demonstrate that the patterns of dependence of the information transmission time on the number of the food-containing branch at the first and third stages of experiments are considerably different. Moreover, in the vicinities of the “special” branches, the time taken for transmission of the information about the number of the branch with the trough is, on the average, shorter. For example, in the first series, at the first stage of the experiments the ants took 70–82 seconds to transmit the information about the fact that the trough with syrup was on branch N 11, and 8–12 seconds to transmit the information about branch N 1. At the third stage it took 5 - 15 seconds to transmit the information about branch N 11. These data enable us to suggest that the ants have changed the mode of presenting the data about the number of the branch containing food.
What about ants’ ability to add and subtract small numbers? Analysis of the time duration of information transmission by the ants raises the possibility that at the third stage of the experiment the scouts’ messages consisted of two parts: the information about which of the “special” branches was the nearest to the branch with the trough, and the information about how many branches away is the branch with the trough from a certain “special” branch. In other words, the ants, presumably, passed the “name” of the “special” branch nearest to the branch with the trough, and then the number which had to be added or subtracted in order to find the branch with the trough. That ant teams went directly to the “correct” branch enables us to suggest that they performed correctly whatever “mental” operation (subtraction or addition) was to be made.
Figure 4.
Dependence of the time (t; measured in seconds) of transmission of information about the number of the branch having food on its ordinal number (i) in the first and the third series of experiments in the ant Formica polyctena. Diamonds, the time taken for transmission of information at the first stage; Squares, the same at the third stage.
Figure 4.
Dependence of the time (t; measured in seconds) of transmission of information about the number of the branch having food on its ordinal number (i) in the first and the third series of experiments in the ant Formica polyctena. Diamonds, the time taken for transmission of information at the first stage; Squares, the same at the third stage.
In order to verify this statistically, the coefficient of correlation was calculated between the time required for transmission of information about the trough being on the branch
i and the distance from
i to the nearest “special” branch. The results confirmed the hypothesis that the time for transmission of a message about the number of the branch is shorter when this branch is closer to any of the “special” ones. For this purpose, the data obtained at the third stage of the experiment were transformed to present them in the form shown in
Table 5 where data of one year are given as an example. In this table we do not include branches that are close to the starting point of the set-up (N 1 - 4) because there is no need to use “arithmetic” for ants where rewarded branches are very close to the first one (in fact ants spent roughly the same time transmitting information about these branches: from 10 to 20 seconds).
It can be seen from
Table 6 that the coefficients of correlation between the transmission time and the distance to the nearest special point have quite high values and they differ significantly from zero. So the results support the hypothesis that the time for transmission of a message about the number of the branch is shorter when this branch is close to either of the special ones. This, in turn, shows that at the third stage of the experiment the ants used simple additions and subtractions, achieving economy in a manner reminiscent of the Roman numeral system when the numbers 10 and 20, 10 and 19 in different series of the experiments, played a role similar to that of the Roman numbers V and X.
Table 5.
Dependence of the time of information transmission (t) on the distance from the branch with a trough to the nearest “special” branch (special branches are 10 and 20).
Table 5.
Dependence of the time of information transmission (t) on the distance from the branch with a trough to the nearest “special” branch (special branches are 10 and 20).
| The number of the branch having food (experiments in different days, consequently) | Distance to the nearest special branch | Times of transmission of information about the branch number for different scouts (sec) |
| 26 | 6 | 35, 30 |
| 30 | 10 | 70, 65 |
| 27 | 7 | 65, 72 |
| 24 | 4 | 58, 60, 62 |
| 8 | 2 | 22, 20, 25 |
| 16 | 4 | 25, 8, 25 |
| 16 | 4 | 25 |
| 22 | 2 | 15, 18 |
| 18 | 2 | 20, 25, 18, 20 |
| 15 | 5 | 30, 28, 35, 30 |
| 20 | 0 | 10, 12, 10 |
| 6 | 4 | 25, 28 |
| 16 | 4 | 30, 25 |
| 15 | 5 | 20, 25, 20 |
| 14 | 4 | 25, 28, 30, 26 |
| 17 | 3 | 17, 15 |
| 11 | 1 | 10, 12 |
Our interpretation is that ants of highly social group-retrieving species are able to add and subtract small numbers. This also indicates that these insects have a communication system with a great degree of flexibility. Until the frequencies with which the food was placed on different branches started exhibiting regularities, the ants were “encoding” each number (i) of a branch with a message of length proportional to i, which suggests unitary coding. Subsequent changes of code in response to special regularities in the frequencies are in line with a basic information-theoretic principle that in an efficient communication system the frequency of use of a message and the length of that message are related.
Table 6.
Values of correlation coefficient (r) in the experiments with different “special” branches. All values differ significantly from zero at the confidence level of 0.99.
Table 6.
Values of correlation coefficient (r) in the experiments with different “special” branches. All values differ significantly from zero at the confidence level of 0.99.
| Sample size | Numbers of “special” branches | r for the first stage of the experiments | r for the third stage of the experiments |
| 150 | 10,20 | 0.95 | 0.80 |
| 92 | 10,19 | 0.96 | 0.91 |
| 99 | 15 | 0.99 | 0.82 |