Statistical Ensemble Theory of Gompertz Growth Model
Abstract
:1. Introduction
2. Distributions Generated from a Self-referential Process
3. On Fluctuation of a Growth Parameter
4. Entropy Revisited
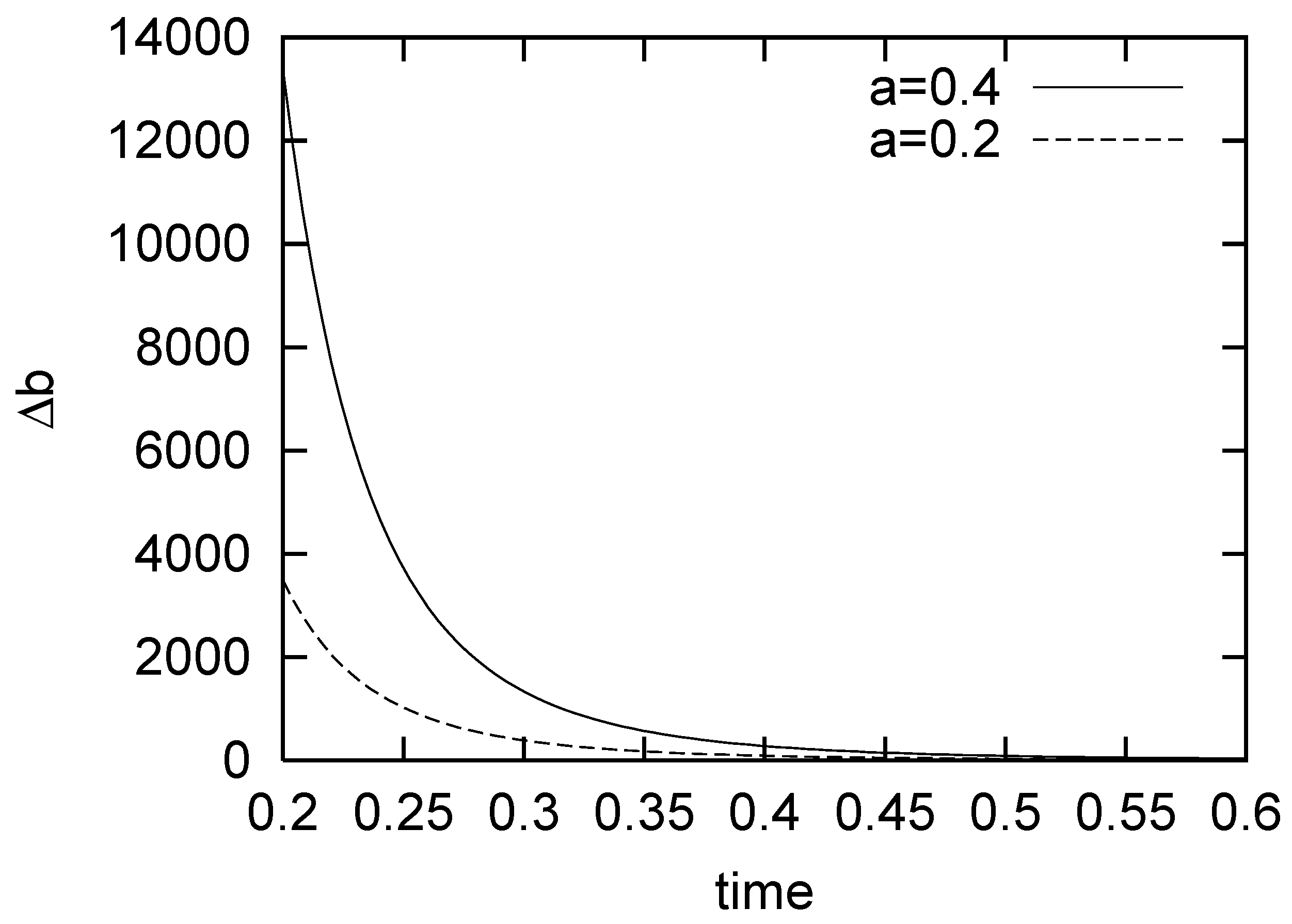
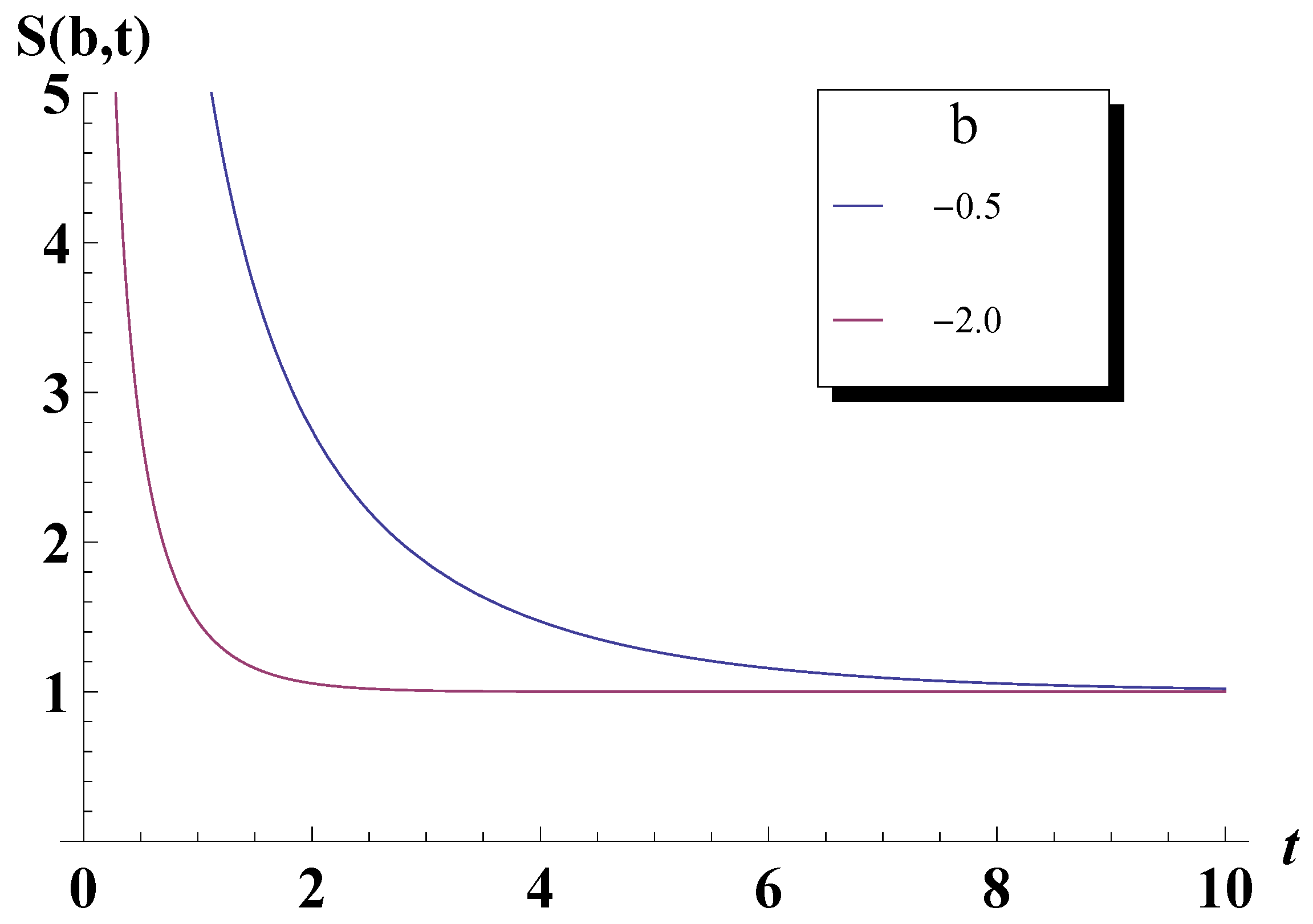
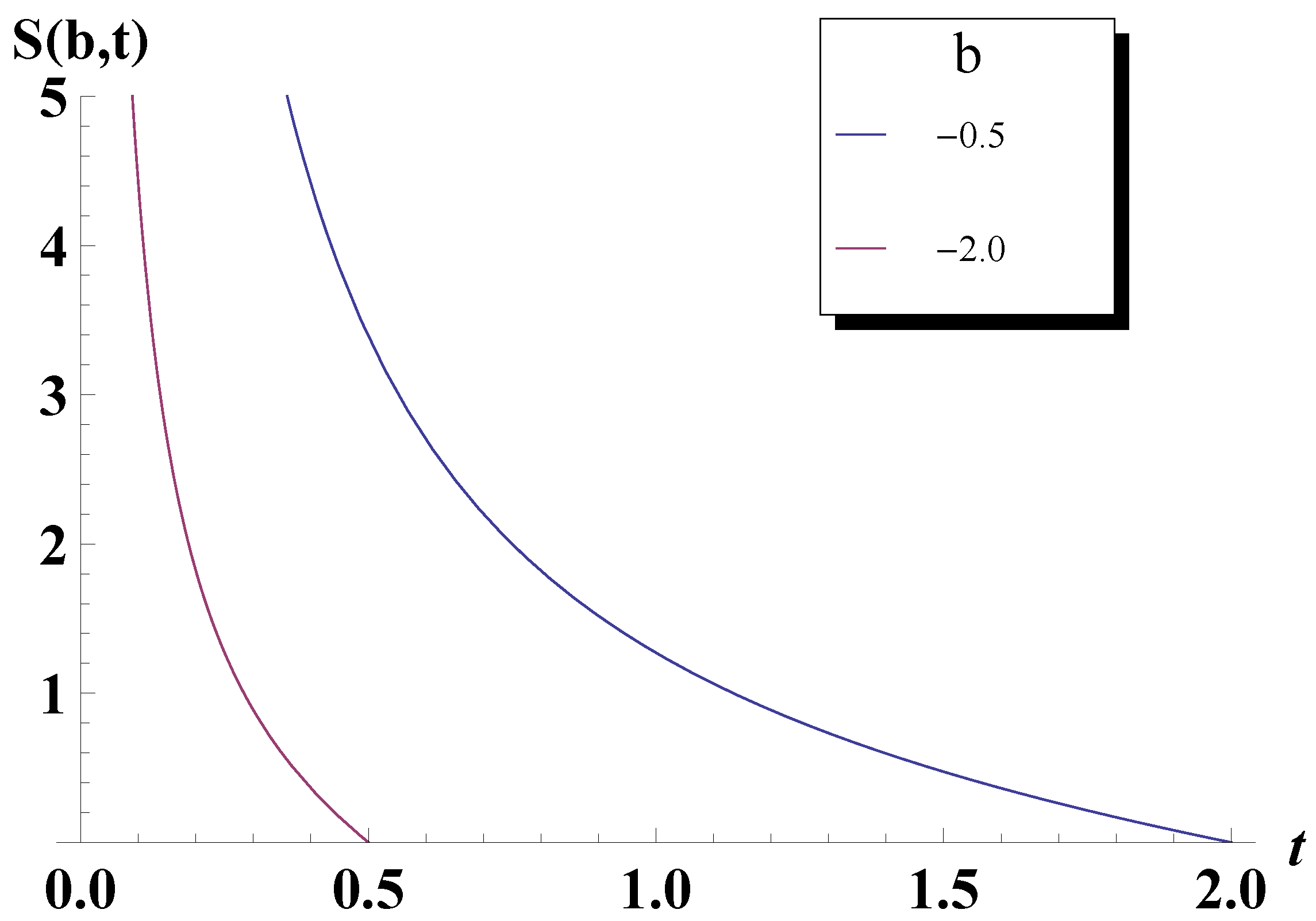
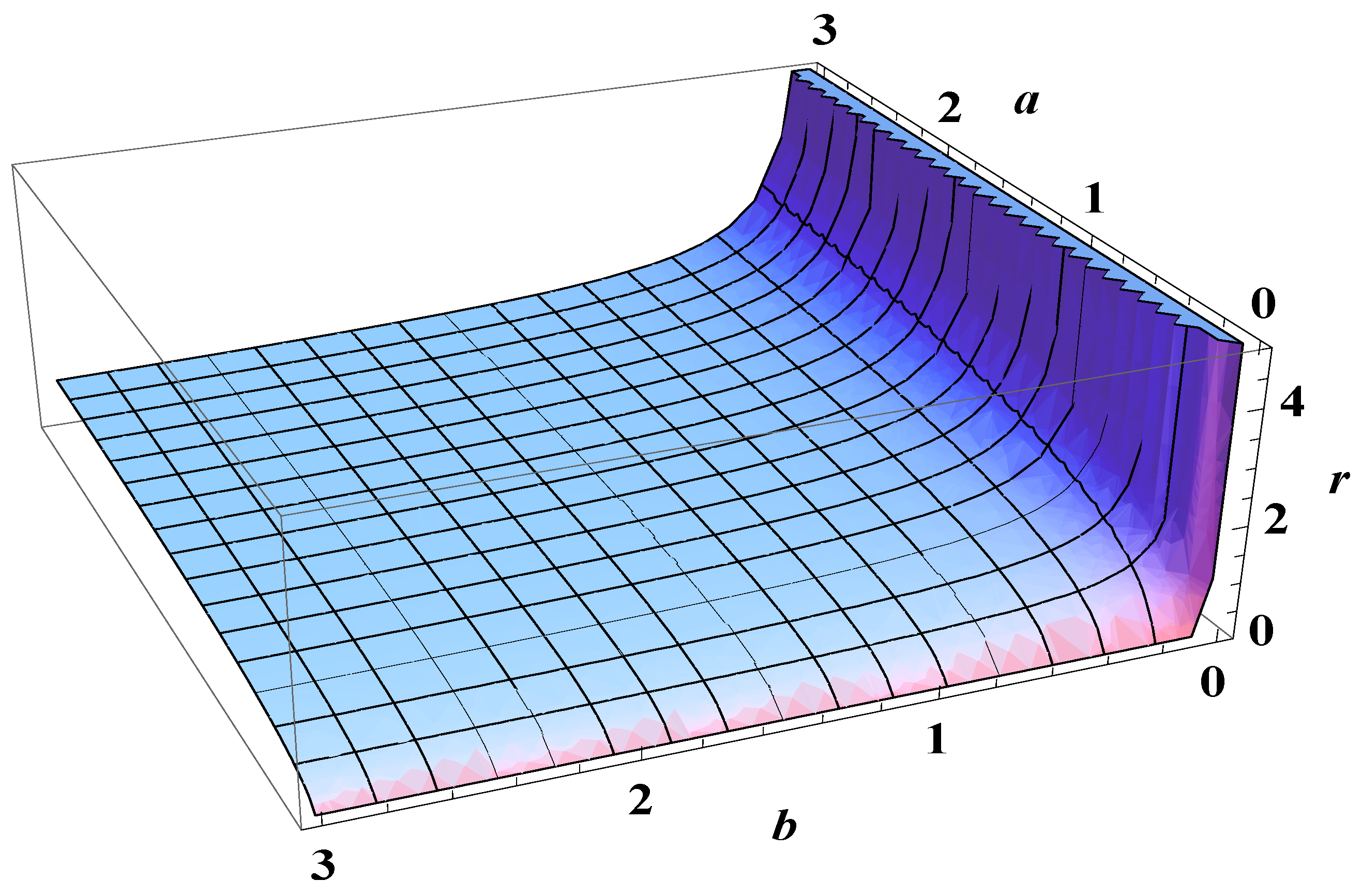
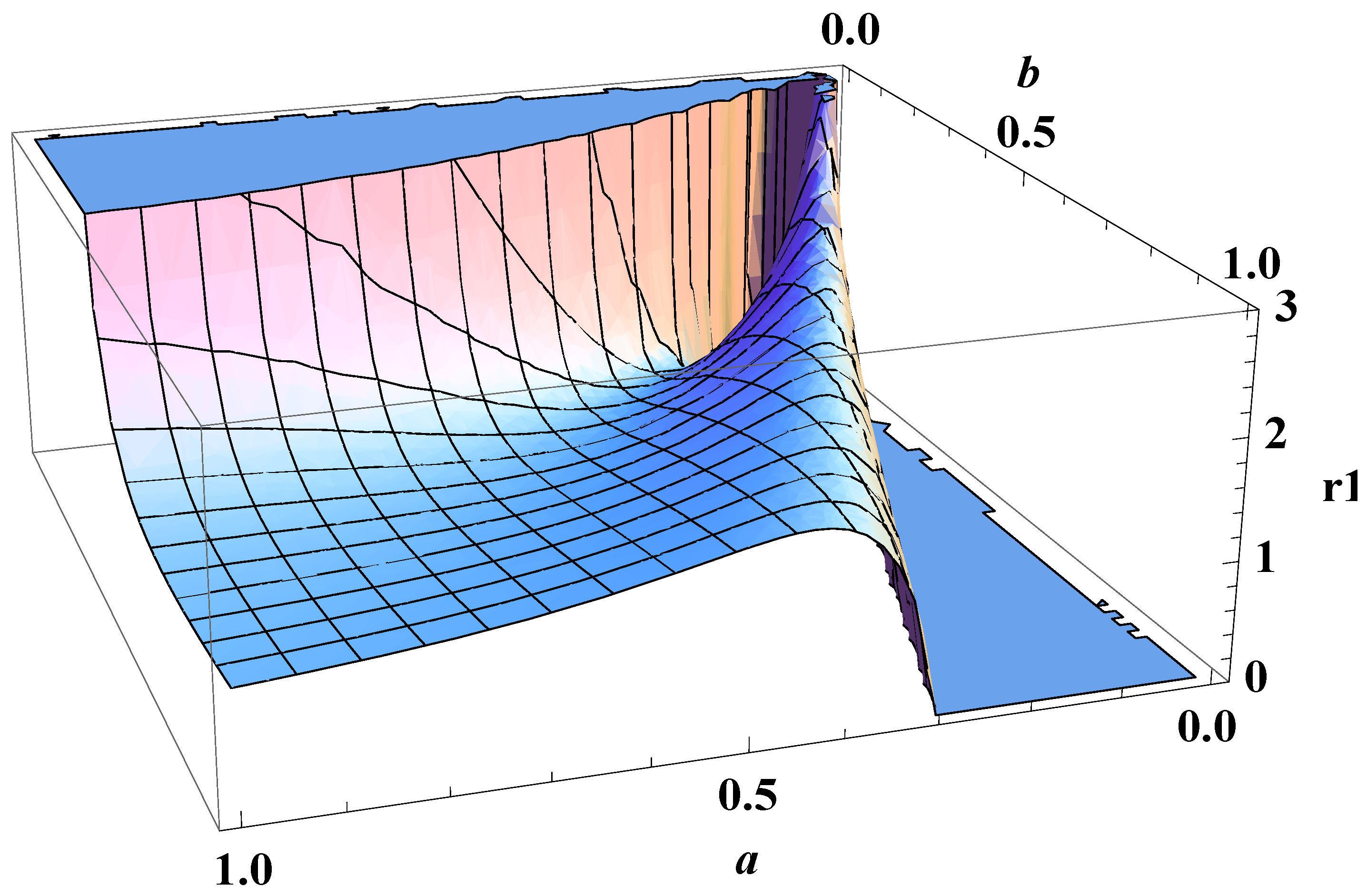
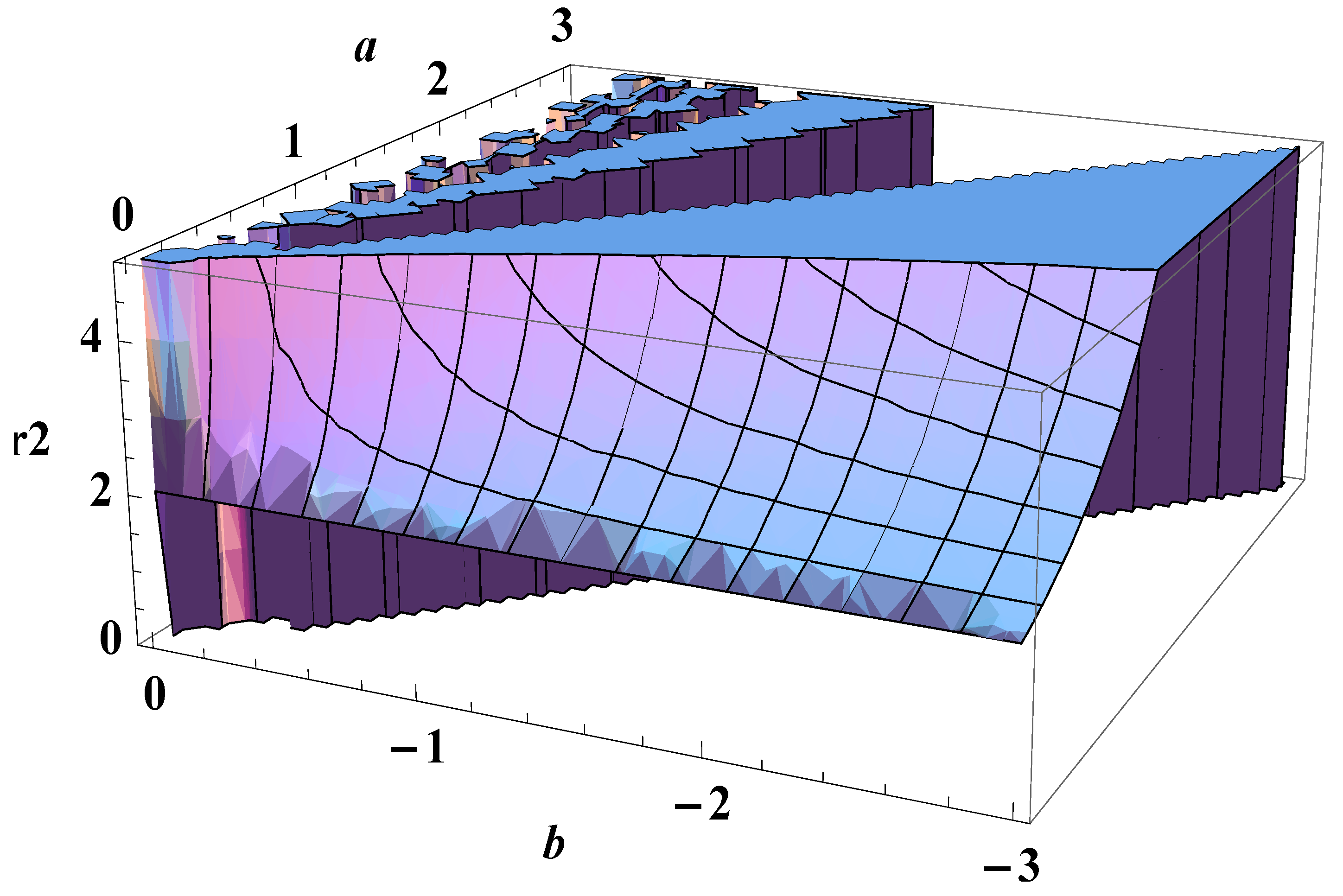
5. Bose-Einstein Condensation Picture for the Gompertz Model
6. Summary and Concluding Remarks
Acknowledgements
References and Notes
- Gompertz, B. On the nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingencies. Phil. Trans. Roy. Soc. 1825, 115, 513–585. [Google Scholar] [CrossRef]
- Casey, A.E. The experimental alteration of malignancy with an homologous mammalian tumour material I. Am. J. Cancer 1934, 21, 760–775. [Google Scholar]
- Bajzer, Z.; Vuk-Pavlovic, S. Mathematical modelling of tumor growth kinetics. In A Survey of Models for Tumor-Immune System Dynamics; Adam, J.A., Bellomo, N., Eds.; Birkhauser Publishing: Basel, Switzerland, 1997; pp. 89–133. [Google Scholar]
- Bajzer, Z. Gompertzian growth as a self-similar and allometric process. Growth Develop. Aging 1999, 63, 3–11. [Google Scholar]
- Kendal, W.S. Gompertzian growth as a consequence of tumor heterogeneity. Math. Biosci. 1985, 73, 103–107. [Google Scholar] [CrossRef]
- Calderón, C.P.; Kwembe, T.A. Modelling tumor growth. Math. Biosci. 1991, 103, 97–114. [Google Scholar] [CrossRef]
- Gunasekaran, N.; Pande, L.K. Log normal distribution for the intrinsic abundance for species from the Gompertz model. J. Theor. Biol. 1982, 98, 301–305. [Google Scholar] [CrossRef]
- Sitaram, B.R.; Varma, V.S. Statistical mechanics of the Gompertz model of interacting species. J. Theor. Biol. 1984, 110, 253–256. [Google Scholar] [CrossRef]
- Castorina, P.; Zappala, D. Tumor Gompertzian growth by cellular energetic balance. Physica A 2006, 365, 473–480. [Google Scholar] [CrossRef]
- Lo, C.F. Stochastic model of tumour cell growth. J. Theor. Biol. 2007, 248, 317–321. [Google Scholar] [CrossRef]
- Waliszewski, P.; Konarski, J. On time-space of nonlinear phenomena with Gompertzian dynamics. Biosystems 2005, 80, 91–97. [Google Scholar] [CrossRef] [PubMed]
- Waliszewski, P. A principle of fractal-stochastic dualism and Gompertzian dynamics of growth and self-organization. Biosystems 2005, 82, 61–73. [Google Scholar] [CrossRef] [PubMed]
- Apostol, B.-F. Euler’s transform and a generalized Omori’s law. Phys. Lett. A 2005, 351, 175–176. [Google Scholar] [CrossRef]
- Swan, G.W. Role of optimal control theory in cancer chemotherapy. Math. Biosci. 1990, 101, 237–284. [Google Scholar] [CrossRef]
- Kuznetsov, V.A.; Makalkin, I.A.; Taylor, M.A.; Perelson, A.S. Nonlinear dynamics of immunogenic tumors: Parameter estimation and global bifurcation analysis. Bull. Math. Biol. 1994, 56, 295–321. [Google Scholar] [CrossRef] [PubMed]
- We have used Mathematica 7 here and also for later calculations of integrations.
- If the interval t ∈ [0, ∞] is set, the integration becomes −f0eaΓ(0, a)/b when a > 0 and b < 0.
- A way out is to introduce a cut-off time or a death time of tumour cells, however we need dynamics to determine the value. Therefore we do not elaborate this point in this paper.
- Ling, Y.; He, B. Entropic analysis of biological growth models. IEEE Trans. Biomed. Eng. 1993, 40, 1193–1200. [Google Scholar] [CrossRef] [PubMed]
- Note that r is different from the proliferation rate in Equation (1).
- The number of indistinguishable particles ni in the energy Ei is given by when there is no degeneracy, where β is the inverse temperature and μ the chemical potential.
- Pathria, R.K. Statistical Mechanics, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 1996. [Google Scholar]
- Abbott, D.; Davis, P.C.; Pati, A.K. Quantum Aspect of Life; Imperial College Press: London, UK, 2008. [Google Scholar]
- Davies, P. A quantum recipe for life. Nature 2005, 437, 819. [Google Scholar] [CrossRef] [PubMed]
- Molski, M.; Konarski, J. Coherent states in Gompertzian growth. Phys. Rev. E 2003, 68, 21916–21922. [Google Scholar] [CrossRef]
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Yamano, T. Statistical Ensemble Theory of Gompertz Growth Model. Entropy 2009, 11, 807-819. https://doi.org/10.3390/e11040807
Yamano T. Statistical Ensemble Theory of Gompertz Growth Model. Entropy. 2009; 11(4):807-819. https://doi.org/10.3390/e11040807
Chicago/Turabian StyleYamano, Takuya. 2009. "Statistical Ensemble Theory of Gompertz Growth Model" Entropy 11, no. 4: 807-819. https://doi.org/10.3390/e11040807
APA StyleYamano, T. (2009). Statistical Ensemble Theory of Gompertz Growth Model. Entropy, 11(4), 807-819. https://doi.org/10.3390/e11040807




