A Lower-Bound for the Maximin Redundancy in Pattern Coding
Abstract
:1. Introduction
1.1. Universal Coding
- First, a deterministic approach judges the performance of in the worst case by the maximal redundancy The lowest achievable maximal redundancy is called minimax redundancy:
- Second, a Bayesian approach consists in providing Θ with a prior distribution π, and then considering the expected redundancy (the expectation is here taken over θ). Let be the coding distribution minimizing The maximin redundancy of class is the supremum of all over all possible prior distributions π:
1.2. Dictionary and Pattern
- a dictionary defined as the sequence of different characters present in x in order of appearance; in the example .
- a pattern defined as the sequence of positive integers pointing to the indices of each letter in Δ; here, .
1.3. Pattern Coding
2. Theorem
3. Proof
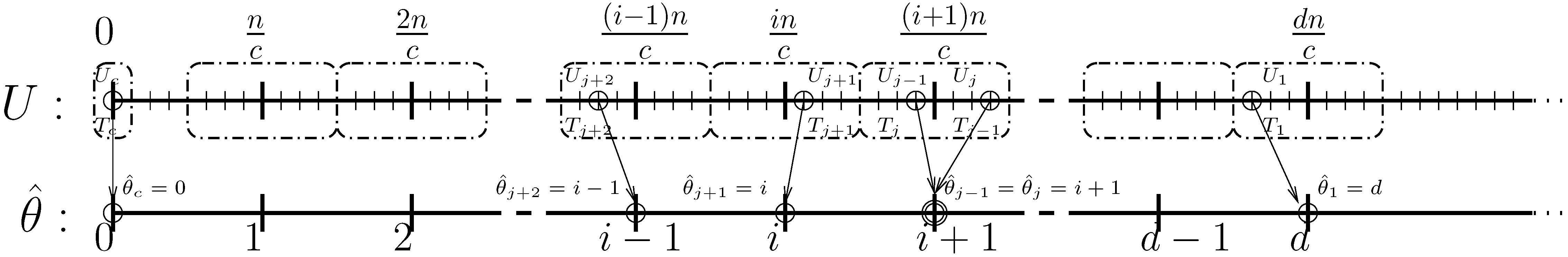
Acknowledgment
References
- Shannon, C.E. A mathematical theory of communication. Bell System Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons Inc.: New York, NY, USA, 1991. [Google Scholar]
- Haussler, D. A general minimax result for relative entropy. IEEE Trans. Inform. Theory 1997, 43, 1276–1280. [Google Scholar] [CrossRef]
- Rissanen, J. Universal coding, information, prediction, and estimation. IEEE Trans. Inform. Theory 1984, 30, 629–636. [Google Scholar] [CrossRef]
- Shields, P.C. Universal redundancy rates do not exist. IEEE Trans. Inform. Theory 1993, 39, 520–524. [Google Scholar] [CrossRef]
- Csiszár, I.; Shields, P.C. Redundancy rates for renewal and other processes. IEEE Trans. Inform. Theory 1996, 42, 2065–2072. [Google Scholar] [CrossRef]
- Kieffer, J.C. A unified approach to weak universal source coding. IEEE Trans. Inform. Theory 1978, 24, 674–682. [Google Scholar] [CrossRef]
- Åberg, J.; Shtarkov, Y.M.; Smeets, B.J. Multialphabet Coding with Separate Alphabet Description. In Proceedings of Compression and complexity of sequences; Press, I.C.S., Ed.; IEEE: Palermo, Italy, 1997; pp. 56–65. [Google Scholar]
- Shamir, G.I.; Song, L. On the entropy of patterns of i.i.d. sequences. In Proceedings of 41st Annual Allerton Conference on Communication, Control and Computing; Curran Associates, Inc.: Monticello, IL, USA, 2003; pp. 160–169. [Google Scholar]
- Shamir, G.I. A new redundancy bound for universal lossless compression of unknown alphabets. In Proceedings of the 38th Annual Conference on Information Sciences and Systems - CISS; IEEE: Princeton, NJ, USA, 2004; pp. 1175–1179. [Google Scholar]
- Shamir, G.I. Universal lossless compression with unknown alphabets-the average case. IEEE Trans. Inform. Theory 2006, 52, 4915–4944. [Google Scholar] [CrossRef]
- Shamir, G.I. On the MDL principle for i.i.d. sources with large alphabets. IEEE Trans. Inform. Theory 2006, 52, 1939–1955. [Google Scholar] [CrossRef]
- Orlitsky, A.; Santhanam, N.P. Speaking of infinity. IEEE Trans. Inform. Theory 2004, 50, 2215–2230. [Google Scholar] [CrossRef]
- Jevtić, N.; Orlitsky, A.; Santhanam, N.P. A lower bound on compression of unknown alphabets. Theoret. Comput. Sci. 2005, 332, 293–311. [Google Scholar] [CrossRef]
- Orlitsky, A.; Santhanam, N.P.; Zhang, J. Universal compression of memoryless sources over unknown alphabets. IEEE Trans. Inform. Theory 2004, 50, 1469–1481. [Google Scholar] [CrossRef]
- Orlitsky, A.; Santhanam, N.P.; Viswanathan, K.; Zhang, J. Limit Results on Pattern Entropy of Stationary Processes. In Proceedings of the 2004 IEEE Information Theory workshop; IEEE: San Antonio, TX, USA, 2004; pp. 2954–2964. [Google Scholar]
- Gemelos, G.; Weissman, T. On the entropy rate of pattern processes; Technical report hpl-2004-159; HP Laboratories Palo Alto: San Antonio, TX, USA, 2004. [Google Scholar]
- Shamir, G.I.; From University of Utah, Electrical and Computer Ingeneering. Private communication, 2006.
- Davisson, L.D. Universal noiseless coding. IEEE Trans. Inform. Theory 1973, IT-19, 783–795. [Google Scholar] [CrossRef]
- Dixmier, J.; Nicolas, J.L. Partitions sans petits sommants. In A Tribute to Paul Erdös; Cambridge University Press: New York, NY, USA, 1990; Chapter 8; pp. 121–152. [Google Scholar]
- Szekeres, G. An asymptotic formula in the theory of partitions. Quart. J. Math. Oxford 1951, 2, 85–108. [Google Scholar] [CrossRef]
- Massart, P. Ecole d’Eté de Probabilité de Saint-Flour XXXIII; LNM; Springer-Verlag: London, UK, 2003; Chapter 2. [Google Scholar]
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license http://creativecommons.org/licenses/by/3.0/.
Share and Cite
Garivier, A. A Lower-Bound for the Maximin Redundancy in Pattern Coding. Entropy 2009, 11, 634-642. https://doi.org/10.3390/e11040634
Garivier A. A Lower-Bound for the Maximin Redundancy in Pattern Coding. Entropy. 2009; 11(4):634-642. https://doi.org/10.3390/e11040634
Chicago/Turabian StyleGarivier, Aurélien. 2009. "A Lower-Bound for the Maximin Redundancy in Pattern Coding" Entropy 11, no. 4: 634-642. https://doi.org/10.3390/e11040634
APA StyleGarivier, A. (2009). A Lower-Bound for the Maximin Redundancy in Pattern Coding. Entropy, 11(4), 634-642. https://doi.org/10.3390/e11040634



