1. Introduction
Electric (gas) discharges appear in various natural phenomena like lightning, St. Elmo’s fire, and spark discharges. Moreover, electric discharges are exploited in various technical devices as lamps, circuit breakers, and plasma torches, to mention a few. Despite of the seniority of the “science of discharges” and the today’s increased computational power, the complexity of the involved physical phenomena like radiative transfer, plasma flow (sometimes supersonic and/or turbulent), electrical contact physics,
etc., still resists a rigorous and general theoretical treatment. Almost eighty years ago, Max Steenbeck wrote in a seminal scientific note [
1], that
at fixed current, the heat power, and thus the voltage drop between the electrodes, is minimized in a real gas discharge. Since then, Steenbeck’s principle has been often used by engineers as a “quick and dirty” approach for modeling electric gas discharge applications [
2]. According to Peters [
3], it can be traced back to Prigogine’s principle of minimum entropy production rate [
4]. Results obtained from these principles often reproduce experimental observations astonishingly well. This fact requires an explanation, because Prigogine’s principle is restricted to linear deviations from thermodynamic equilibrium (for which we will use the terms “weak nonequilibrium” and “near equilibrium”). However, most types of gas discharges exhibit non-ohmic current-voltage relations and are thus beyond linear response (
i.e., “far from equilibrium”).
This article addresses aspects of the pragmatic question, under which circumstances entropy production principles can be helpful for modeling electric discharge phenomena far from equilibrium. “Modeling” will here be associated with relatively simple phenomenological models that provide, for the physical quantities of interest, quantitative predictions, which are probably not exact but serve as estimates with sufficient accuracy for practical purposes. Exhaustive review articles on variational principles for the entropy production rate and similar principles can be found in [
5,
6,
7]. We will first show that Steenbeck’s and Prigogine’s principles are consequences of the maximum entropy production rate principle (MEPP) [
8]. We then illustrate their application by three examples, in order to obtain intuition needed for the somewhat vague (as is in the nature of it) conceptual discussion conducted at the end of this paper.
2. Steenbeck’s Principle from MEPP
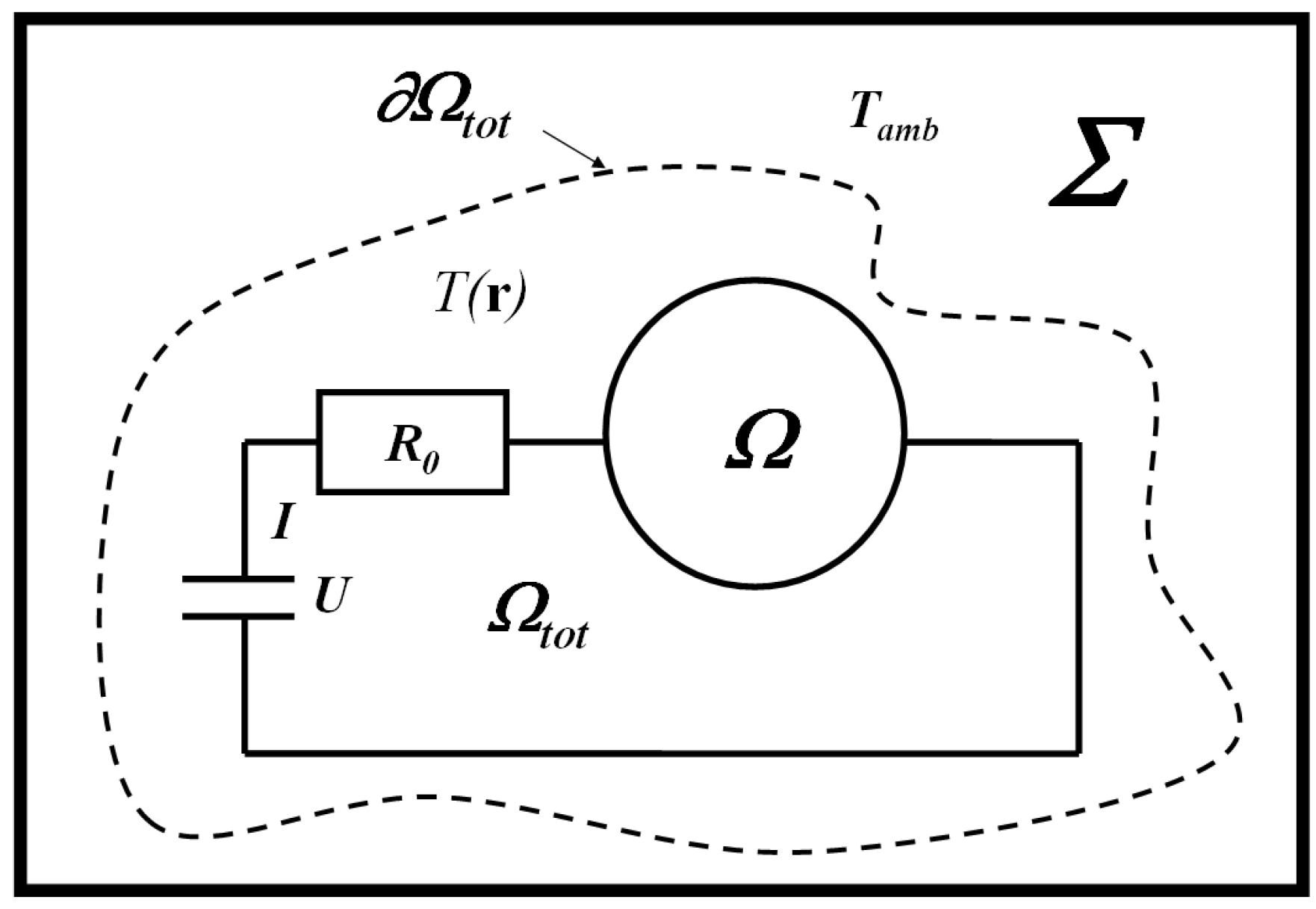
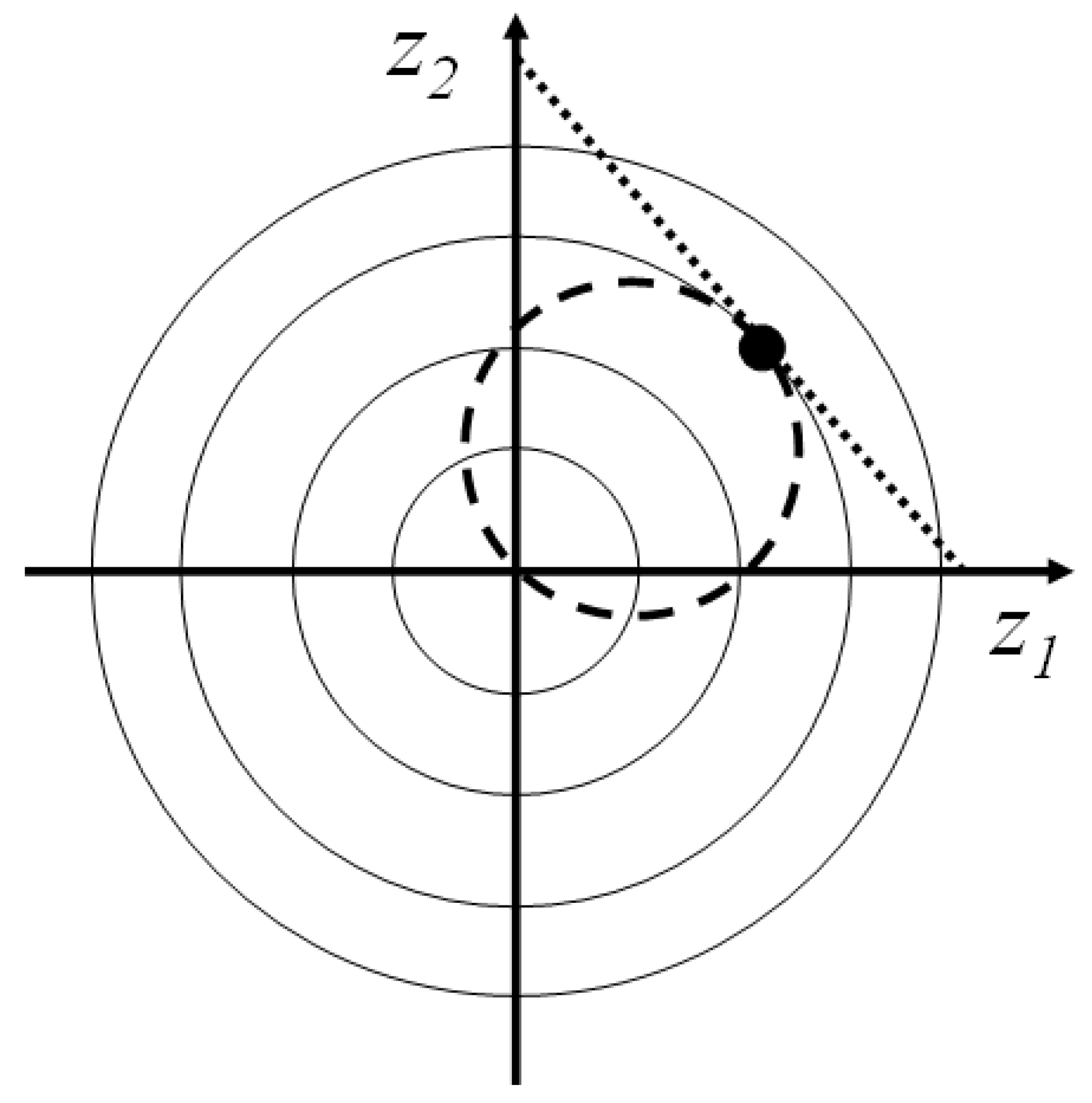
Figure 1 sketches the type of system that will be considered throughout this paper [
8]. It is isolated and consists of a subsystem
, bounded by the dashed curve, and a much larger part, Σ, that acts as a thermal equilibrium heat bath with constant temperature
and that is at electrical ground. The electrical coupling between Σ and
is purely capacitive, and the total charge in each is zero. The boundary
of
is chosen to be at ground potential and at ambient temperature
.
An initial nonequilibrium state is then prepared by charging a battery with energy , and keeping first everything else in at equilibrium ( everywhere and vanishing current ). The battery is assumed to be ideal, i.e., it provides a constant voltage U as long as electric energy is stored, and has zero voltage if it is empty. Leakage losses will be neglected, and series discharge losses in the battery can be included in the general ohmic resistor connected in series to the (fully dissipative) subsystem Ω. The latter, which is in the main focus, is to be modeled later.
When a discharge starts, a constant current I develops. This steady state will have a spatial temperature distribution , . Its discharge duration , defined by the battery being emptied, is assumed to be much longer than the initial and final transient states when the steady state forms and decays, respectively. The final equilibrium state is characterized by a fully discharged battery and again a temperature everywhere. Equality of initial and final temperature is ensured by Σ being a thermodynamic reservoir, i.e., being much smaller than the total thermal energy content of Σ. The initially stored potential energy is eventually fully dissipated into heat. The entropy difference of final and initial states is then . Since the short transient phases can be neglected, the entropy production rate is constant, with P being the steady state power in .
Figure 1.
The isolated nonequilibrium system, consisting of a part with variable temperature inside the dashed boundary (containing a battery with voltage U, a constant resistor , an electrical sub-system Ω), and the heat reservoir Σ at temperature and at ground potential.
Figure 1.
The isolated nonequilibrium system, consisting of a part with variable temperature inside the dashed boundary (containing a battery with voltage U, a constant resistor , an electrical sub-system Ω), and the heat reservoir Σ at temperature and at ground potential.
For simplicity, we suppose that the “device” Ω is only electrically and thermally coupled to its environment, but does not exchange mass or momentum. This device is described by a phenomenological model
for the current voltage relation, containing a number of model parameters
with yet unknown values. Complete information would be given by
N appropriate equations from which
can be determined; the problem would then be solved. We assume, however, that some information on Ω, is missing,
i.e., only part of these equations are known. The goal will then be to determine the values of
with MEPP, using the given equations as constraints. MEPP states that the total system restores equilibrium by maximizing the
entropy production rate (of the quasi-steady state) subject to the given constraints. One of the constraints is total power balance
where
is the power delivered by the battery, and
is the total Joule heat production.
is the heat production of subsystem Ω. As shown above, the total heat production,
P, in
is related to the total entropy production rate
by [
3]
MEPP is here obviously equivalent to maximum total power
. Note that
U is a fixed parameter but
I varies with
. Besides the
total power, only the
ambient temperature appears explicitly in Equation 3, although in
a non-constant temperature distribution,
, generally exists. For instance, if
and
are the temperatures of the resistor
and Ω, respectively,
is
not equal to
, which neglects a part of the entropy production due to heat flow. It is thus crucial to choose the surface
at ambient temperature. Because
(cf.
Figure 1) contributes to dissipation, it is inappropriate to apply Equation 3 to the system Ω only [
8]: the heat production
must not be neglected! But this is exactly what is often implicitly done when Prigogine’s principle of minimum entropy production is used in discharge applications. Prigogine’s principle assumes fixed current, which implies that the main entropy production appears in
outside Ω! Indeed, imposed
I means
and
with finite ratio
. Prigogine’s principle for Ω is thus only valid in leading order
in Equation 3, where terms of order
can be neglected. Of course, Prigogine’s principle works if one minimizes
at constant
I, as is usually done. But this is misleading since
has no physical meaning in general, because its derivation requires a boundary, which encloses the dissipating system Ω, excludes
, and is at constant temperature
(cf. [
3]) - and this boundary does not exist in general.
MEPP refers to maximization of
at fixed
U. This implies maximum current
I under variation of
. Without any qualification, we assume that the given information (
i.e., the constraints) has been used to eliminate as many parameters as possible, and
contains the remaining unknowns. Using
and the mesh rule,
, one obtains then
with
. The maximum entropy production (MEP) state is a local optimum if
,
i.e.,
. Let the solution be denoted by
. In order that
is a maximum, the second derivative
must be negative (semi-) definite. There are two different cases, depending on whether the denominator of the prefactor in Equation 5,
i.e., the differential resistance,
, of the total system is positive or negative. Note that in Equation 5
because
.
In the former case, MEPP requires that
must be positive (semi-)definite. Hence the voltage is a minimum of
as a function of
at constant
I, as stated by Steenbeck’s principle. This is equivalent to saying that the system Ω is minimizing its resistance
. For negative differential resistance of Ω,
, the Steenbeck voltage minimum is a MEP state only in presence of a sufficiently large resistor,
i.e., if
. It is a well-known fact that (macroscopic) electric systems with negative differential conductance must be stabilized with an appropriately large series resistance [
9].
On the other hand, MEPP is also satisfied for a state that maximizes voltage at fixed I and has negative . Usually, a finite voltage maximum does not exist, and this state is for most cases unphysical and characterizes just the extinction of a gas discharge, or its instability and cross-over to a different discharge state.
4. Implications for the Applicability of MEPP
Entropy production rate principles for steady states are generally valid only near equilibrium. Let us first comment on MEPP for this case. According to
Section 2., the maximum and minimum entropy production rate (or power dissipation) principles for steady states are equivalent. Which one applies depends on the convexity properties of the optimization problem as is illustrated in an
Appendix. In the isolated system with fixed total voltage, the current
I is the natural quantity that dynamically adjusts for equilibration, and MEPP applies. Minimization of
is valid if
I is fixed, and
will adjust accordingly. Both cases can be summarized by “minimization of the total resistance”. This result is in line with [
15], where the deeper reason for the type of optimum is claimed to lie in the time reversal behavior of the basic variables. As these authors have shown, this discussion clarifies and rectifies one of Landauer’s arguments [
16] against Prigogine’s principle.
A proof for the general validity of a variational principle beyond linear response does not exist [
17], despite various attempts (see references cited in [
6]). One must also not withhold severe and sometimes justified criticism in the literature against entropy production principles by various authors (see, e.g., [
16,
17,
18,
19]). However, criticism usually disregards the existence of
modeling problems with a lack of information that often appears in practice. The reason for such ignorance can be manifold, but this does not play a role here. Applying entropy production principles can then be helpful even for finding apparently far-from-equilibrium states. Examples have been presented in the previous section, and there are more of them [
6]. On the other hand, it is clearly easy for a critic to “invalidate” the MEPP principle, either by applying it in an inappropriate way or by disregarding relevant constraints, and to produce seemingly disproving results.
The task of MEPP is to determine the values of unknown model parameters,
. The believe is that the MEP state gives a “best” or “most unbiased” estimate on the basis of the available information, which is contained in the model (the choice of
, the expression for
, and the constraints, like balance equations
etc.). This viewpoint has been introduced by Jaynes [
20] in his framework of predictive statistical mechanics, and was further discussed by Jones [
21] and Dewar (see Dewar’s chapter in [
7], p. 41). Because there is no proof at hand, one is led to the following, more pragmatic, questions:
For which cases can MEPP serve as a useful tool? How good is a solution obtained with the help of MEPP?An often heard statement, tempting for using MEPP, is that
an irreversible nonequilibrium system tries to increase its entropy as fast as it can, where “as it can” refers to the constraints. Although not strictly correct in general, it sketches a typical trend behavior of irreversible systems [
20]. Thus, far from equilibrium, MEPP can probably be only justified by the tautology, that
it is a model-parameter estimate based on the assumption of MEP. The results are the more accurate, the higher the quality of the information contained in the model is. An illuminating example is given by Rebhan [
22], who compares the exact shock front solution in an ideal gas with MEPP solutions for all cases, where one of the three hydrodynamic balance equations for mass, momentum, and energy, is disregarded.
Let us illustrate what “quality of information” means in practice for the examples discussed in the previous section. Assuming local thermal equilibrium and a single component fluid description of the arc plasma with known conductivity, the complete information consists in the three hydrodynamic balance equations (together with all initial conditions, boundary conditions, and Ohm’s law). For the arc model above, we used information on the structure of the arc,
i.e., a hot cylinder, and kept only energy balance. Using mass or momentum balance instead, would lead to not nearly as reasonable results. Why? Because the physics of free (high current) arcs is mainly
governed by power balance, due to their significant Joule heat production in the hot plasma column. Energy balance controls the much weaker modes (degrees of freedom) associated with mass and momentum distributions. For example, the mass distribution follows more or less the needs of the power balance: when somewhat more mass is required to satisfy energy balance, it will be sucked into the arc core from the surrounding without significant resistance. Only in the case of a concrete physical mechanism for such resistance, like mass production due to material ablation by radiation of an arc constricted in a tube [
23], or a strong, externally forced mass flow, as in certain types of gas circuit breakers [
24], mass balance may become as predominant as energy balance.
Similarly, the charge injected in the first example is a “weak” mode, because the electrode is able to provide whatever charge is needed. For instance, ohmic contact behavior is exactly reproduced by MEPP in this case. But when the steady state net current becomes of the order of the injection current of the contact, contact physics starts to play a role. In that case, relevant information (i.e., constraints associated with contact physics) is missing in the used model, with the consequence that MEPP becomes worse and worse the larger the current is. As a side remark, we mention that for very low currents diffusion starts to play a role, which is also not covered by the model and thus leads again to wrong MEPP predictions for low voltage (at small ).
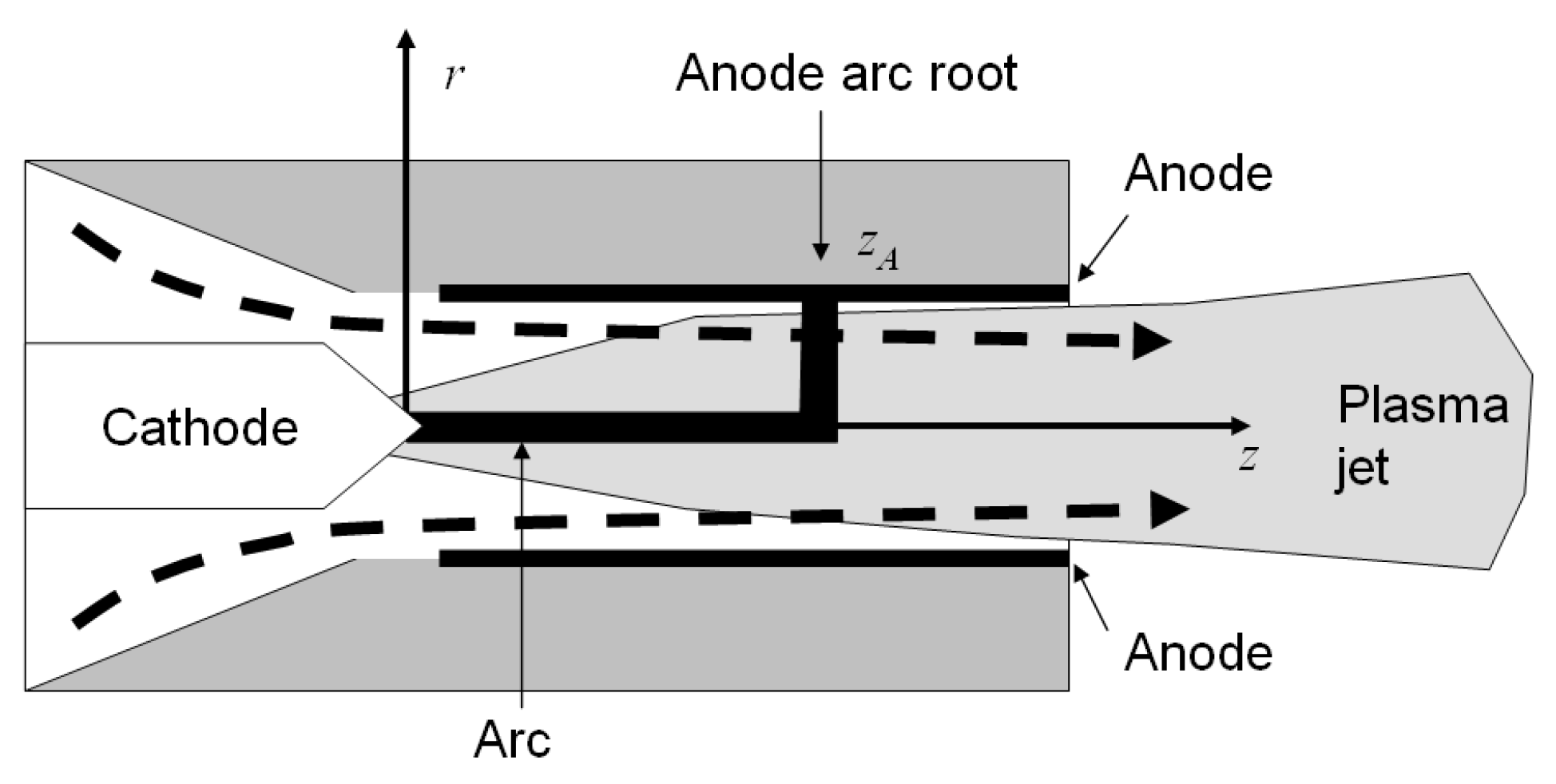
Also the arc attachment location of the torch example is kind of a “weak” mode. The system is axially translationally invariant in the anode region, and the anode column breaks this symmetry. This mode is not in conflict with any local conservation law. But it has a global effect via the dependence of the total voltage, or entropy production rate, on (it is thus not a zero-mode, in contrast to an azimuthal displacement of the anode spot). Again, if forces like magnetic force and drag force become strong, one has to expect that is determined by balancing them, and the MEPP result in its present form is no longer useful due to the inappropriateness of the constraints.
These experiences suggest the conjecture that the applicability of MEPP requires the presence of such a “weak” mode. Although, unfortunately, “weakness” is not clearly defined, it is correlated to the irrelevance of information. In other words, there are many weak, different physical effects of low relevance that would have to be taken into account in the missing equations for , and is rather governed by entropic than energetic driving forces. If there would be a few strong physical forces that outbalance , one would know them. Or, according to Jaynes, if MEPP provides wrong results, one knows that relevant information was overlooked.
A different viewpoint on the interpretation of the occasional success of MEPP is based on work by Kohler [
25], who has shown that for the linearized Boltzmann transport equation entropy production principles are valid. Again, both maximization and minimization principles hold - which one, depends on the type of constraints. In [
26] it has been shown that radiation modeling in the framework of photo-hydrodynamics with an entropy production principle leads to reasonable results arbitrarily far from equilibrium. First, comparison of results suggest that this approach is superior to the often used entropy maximization approach. The reason is that entropy maximization pretends that the system is fully equilibrated on the constraint manifold, while if one considers entropy production rate, equilibration is explicitly taken into account. This is trivially more accurate under nonequilibrium conditions. Secondly, the fact that it works also far from equilibrium is believed to be related to the linearity of the underlying Boltzmann transport equation for the photon gas. As the term “near equilibrium” means “within the approximation of linear deviations from equilibrium”, the considered photon gas is always “near equilibrium” on this kinetic level of description, whatever the photon distribution function looks like. Now the important point: despite of the linearity of the BTE, the resulting equations on the hydrodynamic level are generally strongly nonlinear. This characterizes the system far from equilibrium, even far from local equilibrium! Knowing only the photo-hydrodynamic equations, the underlying linearity is fully hidden. We will show elsewhere that the same can appear for electron transport in matter [
27]. Another example, which points into this direction, is radiation induced material ablation [
28]. There, MEPP was used to determine the vapor temperature and the ablation rate, parameters that enter into the boundary condition of the hydrodynamic balance equations for electric arc simulations. While global mass and energy balance was considered, momentum balance was not used because of local nonequilibrium in the evaporation (Knudsen) layer. The astonishingly good accordance of the MEPP result with experimental observations might also here be related to the behavior of the Knudsen layer to be well approximated by a linearized Boltzmann transport equation.
These observations suggest as a second conjecture, that good results obtained from MEPP for seemingly far from equilibrium systems might rely on a hidden linearity of the underlying Boltzmann transport equation for the concerned quantities.