Non-linear Information Inequalities

Abstract

We construct non-linear information inequalities from Matúš’ infinite series of linear information inequalities. Each single non-linear inequality is sufficiently strong to prove that the closure of the set of all entropy functions is not polyhedral for four or more random variables, a fact that was already established using the series of linear inequalities. To the best of our knowledge, they are the first non-trivial examples of non-linear information inequalities.

1. Introduction

Information inequalities play a crucial role in the proofs for almost all source and channel coding converse theorems. Roughly speaking, these inequalities govern the impossibility in information theory. Among information inequalities discovered to date, the most well-known are the Shannon-type inequalities, including the non-negativity of (conditional) entropies and (conditional) mutual information. In [2], a non-Shannon information inequality (that cannot be deduced from any set of Shannon-type inequalities) involving more than three random variables was discovered. Since then, many additional information inequalities have been discovered [4].

Apart from their application in proving converse coding theorems, information inequalities (either linear or non-linear) were shown to have a very close relation with inequalities involving the cardinality of a group and its subgroups [3]. Specifically, an information inequality is valid if and only if its group-theoretic counterpart (obtained by mechanical substitution of symbols) is also valid. For example, the non-negativity of mutual information is equivalent to the group inequality $\left|G\right||G_1\cap G_2|\ge |G_1\left|\right|G_2|$, where $G_1$ and $G_2$ are subgroups of the group G.

Information inequalities are also the most common tool (perhaps even unique), for the characterization of entropy functions (see Definition 1 below). In fact, entropy functions and information inequalities are two sides of the same coin. A complete characterization for entropy functions requires complete knowledge of the set of all information inequalities.

The set of entropy functions involving n random variables, ${\Gamma }_n^{*}$, and its closure ${\overline{\Gamma }}_n^{*}$ are of extreme importance not only because of their relation to information inequalities [6], but also for determination of the set of feasible multicast rates in communication networks employing network coding [5, 7]. Furthermore, determination of ${\Gamma }^{*}$ would resolve the implication problem of conditional independence (determination of every other conditional independence relation implied by a given set of conditional independence relationships). A simple and explicit characterization of ${\Gamma }^{*}$, and ${\overline{\Gamma }}^{*}$ will indeed be very useful. Unfortunately, except in the case when $n<4$, such a characterization is still missing [1, 2, 4].

Recently, it was shown by Matúš that there are countably infinite many information inequalities [1]. This result, summarized below in Section 2, implies that ${\overline{\Gamma }}_n^{*}$ is not polyhedral. The main result of this paper is non-linear inequalities, which we derive from Matúš’ series in Section 3. To the best of our knowledge this is the first example of a non-trivial non-linear information inequality. We use the non-linear inequality to deduce that the closure of the set of all entropy functions is not polyhedral – a fact previously proved in [1] using the infinite sequence of linear inequalities. Finally, in Section 4, we compare the series of linear inequalities and the proposed nonlinear inequality on a projection of ${\overline{\Gamma }}_n^{*}$.

2. Background

Let the index set $N=\{1,2\cdots ,n\}$ induce a real $2^n$ dimensional Euclidean space ${ℱ}_n$ with coordinates indexed by the set of all subsets of N. Specifically, if $\text{g}\in {ℱ}_n$, then its coordinates are denoted $\left(\text{g}\right(\alpha ):\alpha \subseteq N)$. Consequently, points $\text{𝗀}\in {ℱ}_n$ can be regarded as functions $\text{𝗀}:2^N\mapsto \text{ℝ}$. The focus of this paper is the subset of ${ℱ}_n$ corresponding to (almost) entropic functions.

Definition 1 (Entropic function) 

A function $\text{𝗀}\in {ℱ}_n$ is entropic if $\text{𝗀}(\varnothing )=0$ and there exists discrete random variables $X_1,\cdots ,X_n$ such that the joint entropy of $\{X_i:i\in \alpha \}$ is $\text{𝗀}\left(\alpha \right)$ for all $\varnothing \ne \alpha \subseteq N$. Furthermore, g is almost entropic if it is the limit of a sequence of entropic functions.

Let ${\Gamma }_n^{*}$ be the set of all entropic functions. Its closure ${\overline{\Gamma }}_n^{*}$ (i.e., the set of all almost entropic functions) is well-known to be a closed, convex cone [6]. An important recent result with significant implications for ${\overline{\Gamma }}_n^{*}$ is the series of linear information inequalities obtained by Matúš [1] (restated below in Theorem 1). Using this series, ${\overline{\Gamma }}_n^{*}$ was proved to be non-polyhedral for $n\ge 4$. This means ${\overline{\Gamma }}_n^{*}$ cannot be defined by an intersection of any finite set of linear information inequalities.

Following [1], we will use the following notational conventions. Specific subsets of N will be denoted by concatenation of elements, e.g. 123 will be written for $\{1,2,3\}$. For any $\text{𝗀}\in {ℱ}_n$ and sets $I,J\subseteq N$, define

$$\begin{array}{cc}\hfill {▵}_{I,J}\text{𝗀}& \triangleq \text{𝗀}\left(I\right)+\text{𝗀}\left(J\right)-\text{𝗀}(I\cup J)+\text{𝗀}(I\cap J)\hfill \\ \hfill {☐}_{12,34}\text{𝗀}& \triangleq \text{𝗀}\left(13\right)+\text{𝗀}\left(23\right)+\text{𝗀}\left(14\right)+\text{𝗀}\left(24\right)+\text{𝗀}\left(34\right)\hfill \\ & -\text{𝗀}\left(12\right)-\text{𝗀}\left(3\right)-\text{𝗀}\left(4\right)-\text{𝗀}\left(134\right)-\text{𝗀}\left(234\right).\hfill \end{array}$$

Furthermore, for singletons $i,j,k\in N$, write ${▵}_{ij|k}$ as shorthand for ${▵}_{ik,jk}$.

Theorem 1 (Matúš) 

Let $s\in {\text{ℤ}}^{+},$ the set of positive integers, and $\text{𝗀}\in {\Gamma }_n^{*}$ be the entropy function of discrete random variables $\{X_1,\cdots ,X_n\}$. Then

$$\begin{array}{c}\hfill s\left({☐}_{12,34}\text{𝗀}+{▵}_{34|5}\text{𝗀}+{▵}_{45|3}\text{𝗀}\right)+{▵}_{35|4}\text{𝗀}+\frac{s(s-1)}{2}\left({▵}_{24|3}\text{𝗀}+{▵}_{34|2}\text{𝗀}\right)\ge 0.\end{array}$$

(1)

Furthermore, assuming that $X_5=X_2$, the inequality reduces to

$$\begin{array}{c}\hfill s\left({☐}_{12,34}\text{𝗀}+{▵}_{34|2}\text{𝗀}+{▵}_{24|3}\text{𝗀}\right)+{▵}_{23|4}\text{𝗀}+\frac{s(s-1)}{2}\left({▵}_{24|3}\text{𝗀}+{▵}_{34|2}\text{𝗀}\right)\ge 0.\end{array}$$

(2)

To the best of our knowledge, this is the only result indicating the existence of infinitely many linear information inequalities. Reductions to ${\overline{\Gamma }}_4^{*}$ with $s=1$ recovers the Zhang-Yeung inequality [2] and $s=2$ obtains an inequality of [4].

3. Main Results

3.1. Non-linear information inequalities

The series of information inequalities given in Theorem 1 are all “quadratic” in the parameter $s\in {\text{ℤ}}^{+}$,

$$Q(s;a(\text{𝗀}),b(\text{𝗀}),c(\text{𝗀}\left)\right)\triangleq sb\left(\text{𝗀}\right)+c\left(\text{𝗀}\right)+s(s-1)a\left(\text{𝗀}\right)\ge 0$$

or equivalently

$$\begin{array}{c}\hfill s^{2}a\left(\text{𝗀}\right)+s(b\left(\text{𝗀}\right)-a\left(\text{𝗀}\right))+c\left(\text{𝗀}\right)\ge 0,\end{array}$$

(3)

where in the first series of inequalities (1)

$$\begin{array}{cc}\hfill a\left(\text{𝗀}\right)& \triangleq \frac{1}{2}\left({▵}_{24|3}\text{𝗀}+{▵}_{34|2}\text{𝗀}\right)\hfill \\ \hfill b\left(\text{𝗀}\right)& \triangleq {☐}_{12,34}\text{𝗀}+{▵}_{34|5}\text{𝗀}+{▵}_{45|3}\text{𝗀}\hfill \\ \hfill c\left(\text{𝗀}\right)& \triangleq {▵}_{35|4}\text{𝗀}\hfill \end{array}$$

(4)

and in the second series of inequalities (2)

$$\begin{array}{cc}\hfill a\left(\text{𝗀}\right)& \triangleq \frac{1}{2}\left({▵}_{24|3}\text{𝗀}+{▵}_{34|2}\text{𝗀}\right)\hfill \\ \hfill b\left(\text{𝗀}\right)& \triangleq {☐}_{12,34}\text{𝗀}+{▵}_{34|2}\text{𝗀}+{▵}_{24|3}\text{𝗀}\hfill \\ \hfill c\left(\text{𝗀}\right)& \triangleq {▵}_{23|4}\text{𝗀}.\hfill \end{array}$$

(5)

Proposition 1 

Suppose $\text{𝗀}\in {\mathcal{F}}_n$ satisfies (3) for all positive integers s and $c\left(\text{𝗀}\right)\ge 0$ (or equivalently, $Q(0;a(\text{𝗀}),b(\text{𝗀}),c(\text{𝗀}\left)\right)\ge 0$). Then

• $a\left(\text{𝗀}\right)\ge 0$,
• $a\left(\text{𝗀}\right)=0\Rightarrow b\left(\text{𝗀}\right)\ge 0$, and
• $a\left(\text{𝗀}\right)+b\left(\text{𝗀}\right)+2c\left(\text{𝗀}\right)\ge 0$. Furthermore, equality holds if and only if $a\left(\text{𝗀}\right)=b\left(\text{𝗀}\right)=c\left(\text{𝗀}\right)=0$.

Proof: 

Direct verification. ☐

In the following, we will derive non-linear information inequalities from the sequence of linear inequalities (3).

Theorem 2 

Suppose that $\text{𝗀}\in {\mathcal{F}}_n$ and $b\left(\text{𝗀}\right)\le 2a\left(\text{𝗀}\right)$. Let

$$\begin{array}{c}\hfill w\left(\text{𝗀}\right)\triangleq \left\{\begin{array}{cc}-\frac{b\left(\text{𝗀}\right)-a\left(\text{𝗀}\right)}{2a\left(\text{𝗀}\right)}\hfill & ifa\left(\text{𝗀}\right)>0\hfill \\ 0\hfill & \mathit{otherwise}.\hfill \end{array}\right.\end{array}$$

Then g satisfies (3) for all nonnegative integers s if and only if $a\left(\text{𝗀}\right),c\left(\text{𝗀}\right)\ge 0$ and

$$\begin{array}{c}\hfill {(b\left(\text{𝗀}\right)-a\left(\text{𝗀}\right))}^2-4a\left(\text{𝗀}\right)c\left(\text{𝗀}\right)\le min\left(4a{\left(\text{𝗀}\right)}^2{(w\left(\text{𝗀}\right)-\lfloor w\left(\text{𝗀}\right)\rfloor )}^2,4a{\left(\text{𝗀}\right)}^2{(\lceil w\left(\text{𝗀}\right)\rceil -w\left(\text{𝗀}\right))}^2\right).\end{array}$$

(6)

Proof: 

To simplify notation, $a\left(\text{𝗀}\right),b\left(\text{𝗀}\right)$ and $c\left(\text{𝗀}\right)$ will simply be denoted as $a,b$ and c. We will first prove the only-if part. Assume that g satisfies (3) for all nonnegative integers s. When $s=0$, $c\ge 0$. By Proposition 1, $a\ge 0$. It remains to prove that (6) holds.

Suppose first that $a>0$. If the quadratic $Q(s;a,b,c)$ has no distinct real roots in s, then clearly ${(b-a)}^2-4ac\le 0$ and the theorem holds. On the other hand, if $Q(s;a,b,c)$ has distinct real roots, implying ${(b-a)}^2-4ac>0$, then $Q(s;a,b,c)$ is negative and is at its minimum when $s=-(b-a)/2a$ which is greater than $-1/2$ by assumption.

Since $Q(s;a,b,c)\ge 0$ for all non-negative integer s, the “distance” between the two roots can be at most $2min\left(w-\lfloor w\rfloor ,\lceil w\rceil -w\right)$. In other words,

$$\begin{array}{c}\hfill \frac{\sqrt{{(b-a)}^2-4ac}}{a}\le 2min\left(w-\lfloor w\rfloor ,\lceil w\rceil -w\right)\end{array}$$

or equivalently, ${(b-a)}^2-4ac\le min(4a^2{(w-\lfloor w\rfloor )}^2,4a^2{(\lceil w\rceil -w)}^2)$.

If on the other hand that $a=0$, then the assumption $b\le 2a$ and Proposition 1 implies that $b=0$. As such, the quadratic inequality ${(b-a)}^2-4ac\le 0$ and (6) clearly holds. Hence, the only-if part of the theorem is proved.

Now, we will prove the if-part. If $a=0$, then (6) and the assumption $b\le 2a$ implies that $b=0$. The theorem then holds as $c\ge 0$ by assumption. Now suppose $a>0$ and $b\le 2a$. Using a similar argument as before, (6) implies that either $Q(s;a,b,c)\ge 0$ has no real roots or the two real roots are within the closed interval $[\lfloor w\rfloor ,\lceil w\rceil ]$. Since $a>0$, for all nonnegative integer s, we have $Q(s;a,b,c)\ge 0$, or equivalently, $s^{2}a+s(b-a)+c\ge 0$ and hence the theorem is proved. ☐

Theorem 2 showed that Matúš series of linear inequalities is equivalent to the single non-linear inequality (6) under the condition that that $b\left(\text{𝗀}\right)\le 2a\left(\text{𝗀}\right)$ and $a\left(\text{𝗀}\right),c\left(\text{𝗀}\right)\ge 0$.

Clearly, $a\left(\text{𝗀}\right),c\left(\text{𝗀}\right)\ge 0$ holds for all entropic g because of the nonnegativity of conditional mutual information. Therefore, imposing these two conditions does not very much weaken (6). If on the other hand that $b\left(\text{𝗀}\right)\le 2a\left(\text{𝗀}\right)$ does not hold, then Matúš series of inequalities are implied by that $a\left(\text{𝗀}\right),c\left(\text{𝗀}\right)\ge 0$. In that case, Matúš’ inequalities will not be of interest. Therefore, our proposed nonlinear inequality essentially is not much weaker than Matúš’ ones.

While (6) is interesting in its own right, it is not so easy to work with. In the following, we shall consider a weaker form.

Corollary 1 (Quadratic information inequality) 

Suppose that g satisfies (3) for all nonnegative integers s. If $b\left(\text{𝗀}\right)\le 2a\left(\text{𝗀}\right)$, then

$$\begin{array}{c}\hfill {(b\left(\text{𝗀}\right)-a\left(\text{𝗀}\right))}^2-4a\left(\text{𝗀}\right)c\left(\text{𝗀}\right)\le a{\left(\text{𝗀}\right)}^2.\end{array}$$

(7)

Consequently, if g is almost entropic and ${☐}_{12,34}\text{𝗀}\le 0$ then

$$\begin{array}{c}\hfill {\left({☐}_{12,34}\text{𝗀}+\frac{{▵}_{24|3}\text{𝗀}+{▵}_{34|2}\text{𝗀}}{2}\right)}^2-2({▵}_{24|3}\text{𝗀}+{▵}_{34|2}\text{𝗀}){▵}_{32|4}\text{𝗀}\le \frac{{({▵}_{24|3}\text{𝗀}+{▵}_{34|2}\text{𝗀})}^2}{4}.\end{array}$$

Proof: 

Since $min\left(w\left(\text{𝗀}\right)-\lfloor w\left(\text{𝗀}\right)\rfloor ,\lceil w\left(\text{𝗀}\right)\rceil -w\left(\text{𝗀}\right)\right)\le 1/2$, the corollary then follows directly from Theorem 2. ☐

Despite the fact that the above “quadratic" information inequality is a consequence of a series of linear inequalities, to the best of our knowledge, it is indeed the first non-trivial non-linear information inequality.

3.2. Implications of Corollary 1

In Proposition 1, we showed that Matúš’ inequalities imply that if $a\left(\text{𝗀}\right)=0$, then $b\left(\text{𝗀}\right)\ge 0$. The same result can also be proved by using the quadratic information inequality in (7).

Implication 1 

For any $\text{𝗀}\in {\mathcal{F}}_n$ such that

$$\begin{array}{c}\hfill b\left(\text{𝗀}\right)\le 2a\left(\text{𝗀}\right)\Rightarrow {(b\left(\text{𝗀}\right)-a\left(\text{𝗀}\right))}^2-4a\left(\text{𝗀}\right)c\left(\text{𝗀}\right)\le a{\left(\text{𝗀}\right)}^2,\end{array}$$

(8)

then $a\left(\text{𝗀}\right)=0$ implies $b\left(\text{𝗀}\right)\ge 0$.

Proof: 

If $a\left(\text{𝗀}\right)=0$, then ${(b\left(\text{𝗀}\right)-a\left(\text{𝗀}\right))}^2-4a\left(\text{𝗀}\right)c\left(\text{𝗀}\right)-a{\left(\text{𝗀}\right)}^2=b{\left(\text{𝗀}\right)}^2$. Hence, if $b\left(\text{𝗀}\right)<0$, then (8) will be violated leading to a contradiction. ☐

In [1], it was proved that the cone ${\overline{\Gamma }}_n^{*}$ is not polyhedral for $n\ge 4$. Ignoring the technical details, the idea of the proof is very simple. First, a sequence of entropic functions ${\text{𝗀}}_t$ was constructed such that (1) the sequence converges to ${\text{𝗀}}_0$, and (2) it has a one-side tangent ${\dot{\text{𝗀}}}_{0+}$ which is defined as ${lim}_{t\to 0^{+}}({\text{𝗀}}_t-{\text{𝗀}}_0)/t$. Clearly, if ${\overline{\Gamma }}_n^{*}$ is polyhedral, then there exists $ϵ>0$ such that ${\text{𝗀}}_0+ϵ{\dot{\text{𝗀}}}_{0+}$ is contained in ${\overline{\Gamma }}_n^{*}$. It was then shown that for any $ϵ>0$, the function ${\text{𝗀}}_0+ϵ{\dot{\text{𝗀}}}_{0+}$ is not in ${\overline{\Gamma }}_n^{*}$ because it violates (3) for sufficiently large s. Therefore, ${\overline{\Gamma }}_n^{*}$ is not polyhedral, or equivalently, there are infinitely many information inequalities.

In fact, we can also show that ${\text{𝗀}}_0+ϵ{\dot{\text{𝗀}}}_{0+}$ also violates the quadratic information inequality obtained in Corollary 1 for any positive ϵ. As such, (7) is sufficient to prove that ${\overline{\Gamma }}_n^{*}$ is not polyhedral for $n\ge 4$ and hence the following implication.

Implication 2 

The quadratic inequality (7) is strong enough to imply that ${\overline{\Gamma }}_n^{*}$ is not polyhedral.

Some nonlinear information inequalities are direct consequences of basic linear information inequalities (e.g., $H{\left(X\right)}^{2}I(X;Y)\ge 0$). Such inequalities are trivial in that they are obtained directly as nonlinear transformations of known linear inequalities. Our proposed quadratic inequality (7) is non-trivial, as proved in the following.

Implication 3 

The quadratic inequality (7) is a non-linear inequality that cannot be implied by any finite number of linear information inequalities. Specifically, for any given finite set of valid linear information inequalities, there exists $\text{𝗀}\notin {\overline{\Gamma }}_n^{*}$ such that g does not satisfy (7) but satisfies all the given linear inequalities.

Proof: 

Suppose we are given a finite set of valid linear information inequalities. Then the set of $\text{𝗀}\in {\mathcal{F}}_n$ satisfying all these linear inequalities is polyhedral. In other words, the set is obtained by taking intersection of a finite number of half-spaces. For simplicity, such a polyhedron will be denoted by Ψ.

We will once again use the sequence of entropic functions ${\left\{{\text{𝗀}}_t\right\}}_{t=1}^{\infty }$ constructed in [1]. Clearly, ${\text{𝗀}}_t\in \Psi$ for all t since $\text{𝗀}\in {\Gamma }_n^{*}$. Again, as Ψ is polyhedral, ${\text{𝗀}}_{ϵ}\triangleq {\text{𝗀}}_0+ϵ{\dot{\text{𝗀}}}_{0+}\in \Psi$ for sufficiently small $ϵ>0$. In other words, ${\text{𝗀}}_0+ϵ{\dot{\text{𝗀}}}_{0+}$ satisfies all the given linear inequalities. However, as explained earlier, ${\text{𝗀}}_{ϵ}$ violates the quadratic inequality (7) and hence the theorem follows. ☐

4. Characterizing ${\overline{\Gamma }}_n^{*}$ by projection

Although the set of almost entropic functions ${\overline{\Gamma }}_n^{*}$ is a closed and convex cone, finding a complete characterization is an extremely difficult task. Therefore, instead of tackling the hard problem directly, it is sensible to consider a relatively simpler problem – the characterization of a “projection" of ${\overline{\Gamma }}_n^{*}$. This projection problem is easier because the dimension of a projection can be much smaller, making it easier to be visualized and to be described. Furthermore, its low dimensionality may also facilitate the use of numerical techniques to find an approximation for the projection.

In this section, we consider a particular projection and will show how inequalities obtained in the previous section be expressed by equivalent ones on the proposed projection. As such, we can have a better idea how the projection looks like. First, we will define our proposed projection Υ.

Define ${\rm Y}=\left\{(a\left(\text{𝗀}\right),b\left(\text{𝗀}\right)-a\left(\text{𝗀}\right)):\text{𝗀}\in {\overline{\Gamma }}_n^{*}\text{and}a\left(\text{𝗀}\right)+b\left(\text{𝗀}\right)+2c\left(\text{𝗀}\right)=1\right\}$, or equivalently,

$$\begin{array}{c}\hfill {\rm Y}=\left\{\left(\frac{a\left(\text{𝗀}\right)}{a\left(\text{𝗀}\right)+b\left(\text{𝗀}\right)+2c\left(\text{𝗀}\right)},\frac{b\left(\text{𝗀}\right)-a\left(\text{𝗀}\right)}{a\left(\text{𝗀}\right)+b\left(\text{𝗀}\right)+2c\left(\text{𝗀}\right)}\right):\text{𝗀}\in {\overline{\Gamma }}_n^{*}\text{and}\text{𝗀}\ne \mathbf{0}\right\}.\end{array}$$

(9)

Lemma 1 

Υ is a closed and convex set.

Proof: 

Since the set $\{(a\left(\text{𝗀}\right),b\left(\text{𝗀}\right)-a\left(\text{𝗀}\right)):\text{𝗀}\in {\overline{\Gamma }}_n^{*}\}$ is a closed and convex one, its cross-section (and its affine transform) Υ is also closed and convex. ☐

Since Υ is obtained by projecting ${\overline{\Gamma }}_n^{*}$ onto a two-dimensional Euclidean space, any inequality satisfied by all points in Υ induces a corresponding information inequality. Specifically, we have the following proposition.

Proposition 2 

Suppose that there exists $k\ge 0$ such that

$$\begin{array}{c}\hfill {(a+b+2c)}^k\psi \left(\frac{a}{a+b+2c},\frac{b-a}{a+b+2c}\right)\ge 0ifa=b=c=0.\end{array}$$

(10)

Then

$$\begin{array}{c}\hfill \psi (u,v)\ge 0,\forall (u,v)\in {\rm Y}\end{array}$$

(11)

if and only if

$$\begin{array}{c}\hfill {(a\left(\text{𝗀}\right)+b\left(\text{𝗀}\right)+2c\left(\text{𝗀}\right))}^k\psi \left(\frac{a\left(\text{𝗀}\right)}{a\left(\text{𝗀}\right)+b\left(\text{𝗀}\right)+2c\left(\text{𝗀}\right)},\frac{b\left(\text{𝗀}\right)-a\left(\text{𝗀}\right)}{a\left(\text{𝗀}\right)+b\left(\text{𝗀}\right)+2c\left(\text{𝗀}\right)}\right)\ge 0,{\forall }_{\text{𝗀}}\in {\overline{\Gamma }}_n^{*}.\end{array}$$

(12)

Similarly, (11) holds for all $(u,v)\in {\rm Y}$ and $v\le u$ if and only if (12) holds for all $\text{𝗀}\in {\overline{\Gamma }}_n^{*}$ and $b\left(\text{𝗀}\right)\le 2a\left(\text{𝗀}\right)$.

Proof: 

First, we will prove that (11) implies (12). For any $\text{𝗀}\in {\overline{\Gamma }}_n^{*}$. If $a\left(\text{𝗀}\right)+b\left(\text{𝗀}\right)+2c\left(\text{𝗀}\right)=0$, then by Proposition 1, $a\left(\text{𝗀}\right)=b\left(\text{𝗀}\right)=c\left(\text{𝗀}\right)=0$ and (12) follows from (10). Otherwise, $a\left(\text{𝗀}\right)+b\left(\text{𝗀}\right)+2c\left(\text{𝗀}\right)>0$ and (12) follows from (9).

Conversely, for any $(u,v)\in {\rm Y}$, by definition, there exists $\text{𝗀}\in {\overline{\Gamma }}_n^{*}$ such that (1) $\text{𝗀}\ne 0$ and (2) $u=a\left(\text{𝗀}\right)/\left(a\right(\text{𝗀})+b(\text{𝗀})+2c(\text{𝗀}\left)\right)$ and $v=b\left(\text{𝗀}\right)-a\left(\text{𝗀}\right)/\left(a\right(\text{𝗀})+b(\text{𝗀})+2c(\text{𝗀}\left)\right)$. The inequality (11) then follows from (12) and that $\text{𝗀}\ne 0$ (hence, $a\left(\text{𝗀}\right)+b\left(\text{𝗀}\right)+2c\left(\text{𝗀}\right)>0$).

Finally, the constrained counterpart follows from that $\left(b\right(\text{𝗀})-a(\text{𝗀}\left)\right)\le a\left(\text{𝗀}\right)$ if and only if $b\left(\text{𝗀}\right)\le 2a\left(\text{𝗀}\right)$. ☐

By Proposition 2, there is a mechanical way to rewrite inequalities for ${\overline{\Gamma }}_n^{*}$ as ones for Υ, and vice versa. Therefore, we will abuse notations by calling that (11) and (12) equivalent. In the following, we will rewrite inequalities obtained in previous sections by using Proposition 2.

Proposition 3 (Matúš’ inequalities) 

When s is a positive integer, the inequality (3) is equivalent to

$$\begin{array}{c}\hfill v\ge \frac{2u-2s^{2}u-1}{2s-1}.\end{array}$$

(13)

Proof: 

A direct consequence of Proposition 2 and that

$$\begin{array}{c}\hfill \frac{c\left(\text{𝗀}\right)}{a\left(\text{𝗀}\right)+b\left(\text{𝗀}\right)+2c\left(\text{𝗀}\right)}=\frac{1}{2}\left(1-\frac{b\left(\text{𝗀}\right)-a\left(\text{𝗀}\right)}{a\left(\text{𝗀}\right)+b\left(\text{𝗀}\right)+2c\left(\text{𝗀}\right)}-2\frac{a\left(\text{𝗀}\right)}{a\left(\text{𝗀}\right)+b\left(\text{𝗀}\right)+2c\left(\text{𝗀}\right)}\right).\end{array}$$

(14)

☐

By optimizing the choice of s, we can obtain a stronger piecewise linear inequality which can be rewritten as follows.

Theorem 3 (Piecewise linear inequality) 

The piecewise linear inequality

$$\begin{array}{c}\hfill \underset{s\in {\mathbb{Z}}^{+}}{min}{s}^{2}a\left(\text{𝗀}\right)+s(b\left(\text{𝗀}\right)-a\left(\text{𝗀}\right))+c\left(\text{𝗀}\right)\ge 0\end{array}$$

(15)

is equivalent to that

$$\begin{array}{c}\hfill v\ge L^{li}\left(u\right),\end{array}$$

(16)

where $L^{li}\left(u\right)\triangleq {sup}_{s\in {\mathbb{Z}}^{+}}(2u-2s^{2}u-1)/(2s-1)$.

Proof: 

A direct consequence of Propositions 2 and 3. ☐

As we shall see in the following lemma, $L^{li}\left(u\right)$ can be explicitly characterized.

Lemma 2 

$L^{li}\left(0\right)=0$ and

$$L^{li}\left(u\right)=(2u-2s_o^{2}u-1)/(2s_o-1)$$

for any $0<u\le 1$, where $s_o$ is the smallest positive integer such that $1/(1+2s_o^2)\le u$.

Proof: 

Let $f(s,u)\triangleq (2u-2s^{2}u-1)/(2s-1)$. First, $f(s,0)=-1/(2s-1)$. Therefore, $L^{li}\left(0\right)={sup}_{s\in {\mathbb{Z}}^{+}}f(s,0)=0$. Also, it is straightforward to prove that

• for any fixed $u\ge 1/2$, $f(s,u)$ is a decreasing function of s and hence ${sup}_{s\in {\mathbb{Z}}^{+}}f(s,u)=f(1,u)=-1$.
• for $0<u\le 1/2$, $f(s,u)$ is a strictly concave function of s for $s\ge 1$ and is at its maximum when $s=\frac{1}{2}+\sqrt{\frac{1}{2u}-\frac{3}{4}}\ge 1$. As a result, $L^{li}\left(u\right)=max(f(s_l,u),f(s_h,u))$ where $s_l=\lfloor \frac{1}{2}+\sqrt{\frac{1}{2u}-\frac{3}{4}}\rfloor$ and $s_h=⌈\frac{1}{2}+\sqrt{\frac{1}{2u}-\frac{3}{4}}⌉$.
  Clearly, for any positive integer $s_o$,

  $$L^{li}\left(u\right)=\left\{\begin{array}{cc}f(s_o,u)\hfill & \text{if}u=1/2(1-s_o+s_o^2)\hfill \\ f(s_o+1,u)\hfill & \text{if}u=1/2(1+s_o+s_o^2)\hfill \end{array}\right..$$

  Furthermore, if $1/2(1+s_o+s_o^2)<u<1/2(1-s_o+s_o^2)$, we have $s_l=s_o$ and $s_h=s_o+1$ and hence,

  $$\begin{array}{cc}\hfill L^{li}\left(u\right)& =max\left(\frac{2u-2s_o^{2}u-1}{2s_o-1},\frac{-4s_{o}u-2s_o^{2}u-1}{2s_o+1}\right).\hfill \end{array}$$

  (17)

  By solving a system of linear equations, we can show that $f(s_o,u)=f(s_o+1,u)$ if and only if $u=1/(1+2s_o^2)$. Therefore,

  $$L^{li}\left(u\right)=\left\{\begin{array}{cc}f(s_o+1,u)\hfill & \text{if}1/2(1+s_o+s_o^2)<u\le 1/(1+2s_o^2)\hfill \\ f(s_o,u)\hfill & \text{if}1/(1+2s_o^2)\le u\le 1/2(1-s_o+s_o^2).\hfill \end{array}\right.$$

Together with the fact that $L^{li}\left(u\right)=-1=f(1,u)$ for $1/2\le u\le 1$, the lemma follows. ☐

Proposition 4 (Quadratic inequality) 

The quadratic inequality (7) (subject to that $b\left(\text{𝗀}\right)\le 2a\left(\text{𝗀}\right)$) is equivalent to

$$\begin{array}{c}\hfill {(v+u)}^2+2u^2\le 2u\end{array}$$

(18)

subject to that $v\le u$.

Proof: 

By using Proposition 2 and (14), it is straightforward to rewrite (7) as (18). ☐

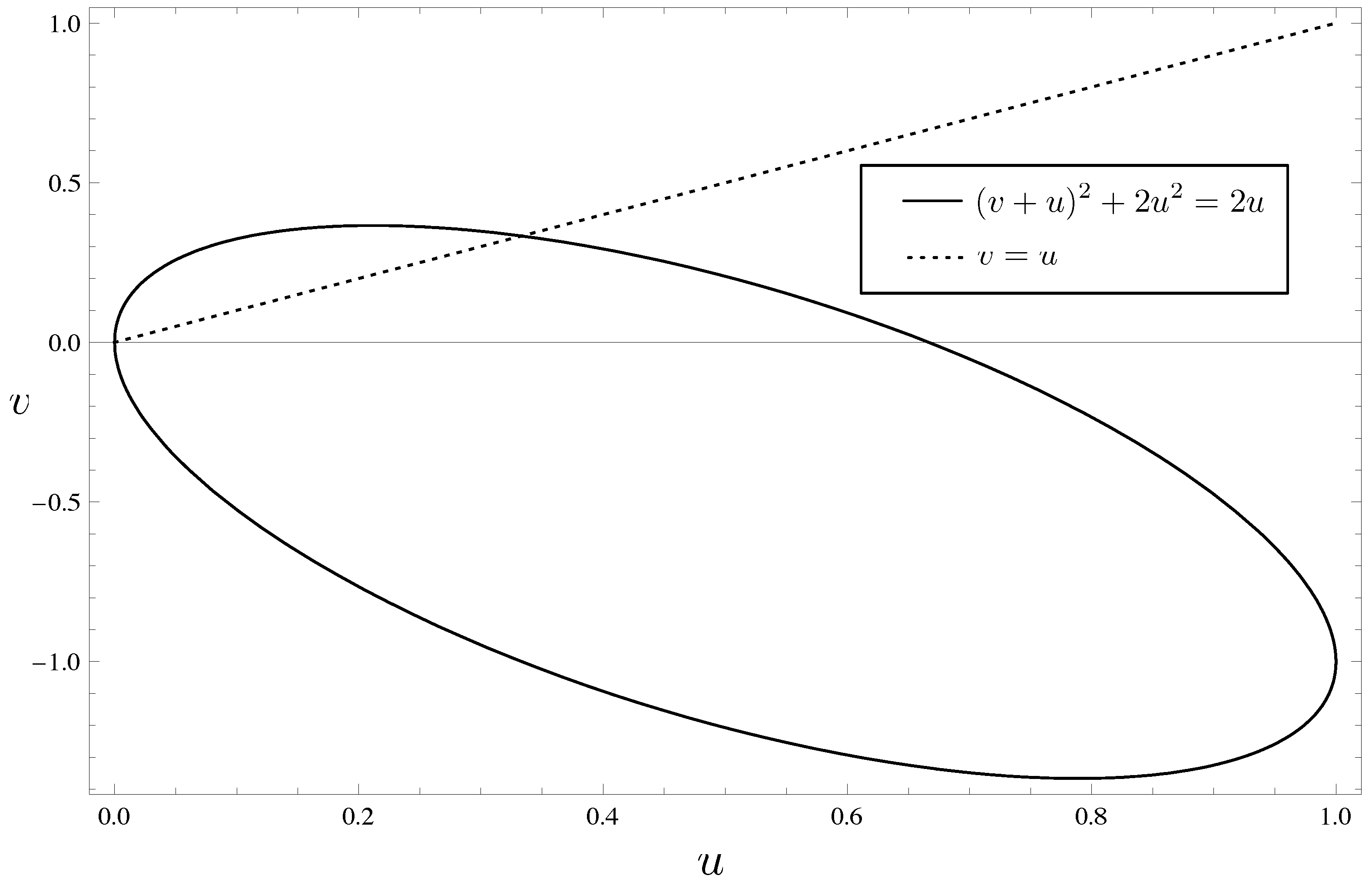
To illustrate (18), we plot the curves ${(v+u)}^2+2u^2=2u$ and $v=u$ in Figure 1. From the proposition, if $v\le u$ (i.e., the point $(u,v)$ is below the dotted line), then $(u,v)\in {\rm Y}$ implies that $(u,v)$ is inside the ellipse.

Proposition 4 gives a nonlinear information inequality on Υ subject to a condition that $v\le u$. In the following theorem, we relax the inequality so as to remove the condition.

Figure 1. Quadratic inequality (18).

Figure 1. Quadratic inequality (18).

Theorem 4 (Non-linear inequality) 

Let

$$\begin{array}{c}\hfill L^{nl}\left(u\right)=-u-\sqrt{2u-2u^2}.\end{array}$$

(19)

For any $(u,v)\in {\rm Y}$, $v\ge L^{nl}\left(u\right)$. Consequently, by Proposition 2,

$$\begin{array}{cc}\hfill b\left(\text{𝗀}\right)& \ge -\sqrt{2a\left(\text{𝗀}\right)(a\left(\text{𝗀}\right)+b\left(\text{𝗀}\right)+2c\left(\text{𝗀}\right))-2a{\left(\text{𝗀}\right)}^2}\hfill \end{array}$$

(20)

$$\begin{array}{cc}& =-\sqrt{2a\left(\text{𝗀}\right)\left(b\right(\text{𝗀})+2c(\text{𝗀}\left)\right)}\hfill \end{array}$$

(21)

Proof: 

By Proposition 4, if $(u,v)\in {\rm Y}$ such that $v\le u$, then

$${(v+u)}^2+2u^2\le 2u.$$

As a result, $v+u\ge -\sqrt{2u-2u^2}$ or equivalently, $v\ge -u-\sqrt{2u-2u^2}.$ On the other hand, if $v\ge u$, then $v\ge 0$ and hence $v\ge -u-\sqrt{2u-2u^2}$. The theorem then follows from Proposition 2. ☐

In the next proposition, we will show that the piecewise linear inequality $v\ge L^{li}\left(u\right)$ and the proposed nonlinear inequality $v\ge L^{nl}\left(u\right)$ coincides for countably infinite number of u.

Proposition 5 

For any $0\le u\le 1$, we have $L^{nl}\left(u\right)\le L^{li}\left(u\right)$. Furthermore, equality holds if $u=1/(1+2s^2)$ for some nonnegative integer s.

Proof: 

By definition, $L^{nl}\left(0\right)=L^{li}\left(0\right)=0$ and the proposition holds in this case. Assume now that $0<u\le 1$. We first show that $L^{nl}\left(u\right)=L^{li}\left(u\right)$ when $u=1/(1+2s^2)$ for some nonnegative integer s. Suppose that $s=0$, then $L^{nl}\left(u\right)=L^{li}\left(u\right)=-1$. On the other hand, if $u=1/(1+2s^2)$ where s is a positive integer, then it is straightforward to prove that

$$\begin{array}{c}\hfill L^{li}\left(u\right)=f(s,u)=f(s+1,u)=\frac{-1-2s}{1+2s^2}=L^{nl}\left(u\right).\end{array}$$

(22)

Figure 2. Piecewise linear inequality and nonlinear inequality.

Figure 2. Piecewise linear inequality and nonlinear inequality.

By differentiating $L^{nl}\left(u\right)$ with respect to u, we can prove that $L^{nl}\left(u\right)$ is convex over $[0,1]$. For each nonnegative integer s, $L^{li}\left(u\right)$ is linear over the interval $[1/(1+2{(s+1)}^2),1/(1+2s^2)]$ and $L^{nl}\left(u\right)=L^{li}\left(u\right)$ when $u=1/(1+2s^2)$ or $1/(1+2{(s+1)}^2)$. Hence, $L^{li}\left(u\right)\ge L^{nl}\left(u\right)$ over the interval by the convexity of $L^{nl}\left(u\right)$. As s can be arbitrarily large, $L^{li}\left(u\right)\ge L^{nl}\left(u\right)$ for $u\in (0,1]$ and the theorem then follows. ☐

5. Conclusion

In this paper, we constructed several piecewise linear and quadratic information inequalities from a series of information inequalities proved in [1]. Our proposed nonlinear inequality (6) was shown to be equivalent to the whole set of Matúš’ linear inequalities. Hence, we can replace all Matúš’ inequalities with our proposed ones.

However, the inequality is not smooth and may not be easy to work with. Therefore, we relax these nonlinear inequalities to quadratic ones. These quadratic inequalities are strong enough to show that the set of almost entropic functions is not polyhedral.

It is certain that the proposed quadratic inequalities we obtained in (16) and (19) are a consequence of Matúš’ linear inequalities. Yet, the non-linear inequality has a much simpler form. By comparing the inequalites on projections of ${\overline{\Gamma }}_n^{*}$, our figures suggested that these nonlinear inequalities are indeed fairly good approximations to the corresponding piecewise linear inequalities. Furthermore, they are of particular interest for several reasons.

First, all these inequalities are non-trivial and cannot be deduced from any finite number of linear information inequalities. To the best of our knowledge, they are the first non-trivial nonlinear information inequalities. Second, in some cases, it will be relatively easier to work with a single nonlinear inequality, rather than an infinite number of linear inequalities. For example, in order to compute some bounds on a capacity region (say, in a network coding problem), a characterization of ${\overline{\Gamma }}_n^{*}$ may be needed as input to a computing system. Surely, ${\overline{\Gamma }}_n^{*}$ is unknown and hence an outer bound of ${\overline{\Gamma }}_n^{*}$ will be used instead. If one replace the countably infinite number of linear inequalities with a single nonlinear inequality, it may greatly simplify the computing problem. Third, these nonlinear inequalities prompt us to ask new fundamental questions - are nonlinear information inequalities more fundamental than linear information inequalities? Would it be possible that the set ${\overline{\Gamma }}_n^{*}$ be completely characterized by a finite number of nonlinear inequalities? If so, what will they look like?

As a final remark, Matúš’ inequalities, and also all the non-linear inequalities we obtained, are “tighter” than the Shannon inequalities only in the region where $b\left(\text{𝗀}\right)\le 2a\left(\text{𝗀}\right)$. When $b\left(\text{𝗀}\right)\ge 2a\left(\text{𝗀}\right)$, the two inequalities are direct consequences of non-negativity of conditional mutual information. This phenomenon seems to suggest that entropic functions are much more difficult to characterize in the region $b\left(\text{𝗀}\right)<2a\left(\text{𝗀}\right)$. An explanation for this phenomenon is still lacking.