1. Introduction
Lin [
12,
13,
14] introduced a new notion of entropy, called
static entropy. His aim was to revise information theory in order to broaden the notion of entropy such that the naturally occurring phenomenon of increased symmetry of a system and the increased similarity of its components may be explained by information theoretic principles.
He proposed that entropy is the degree of symmetry and information is the degree of asymmetry of a structure. With respect to the second law of thermodynamics (which states that entropy of an isolated system increases to a maximum at equilibrium) any spontaneous (or irreversible) process evolves towards a state of maximum symmetry. Many instances of spontaneous processes of different types exist in nature: molecular interaction, phase separation and phase transition, symmetry breaking and the densest molecular packing, crystallization, self-aggregation, self-organization, chemical processes used to separate or purify different substances. These are just a few of the many examples of processes which, according to Lin, are inherently driven by an information minimization or symmetry maximization process.
Spontaneous processes lead to products that are simpler and have a more regular (more symmetric) structure of a lower information content. As Lin [
13] suggests, in a heterogenous structure consisting of a rich variety of components, temperature plays a key role in controlling the direction of a process. Increasing it leads to a homogeneous mixing of the components while decreasing it leads to a spontaneous phase separation of the components that differ. The latter leads to a system of a lesser information content.
We assert that Lin’s notion of information with regards to such processes is better represented by the information needed to describe an object (algorithmic information) rather than Shannon’s notion of information and entropy which is applicable to settings underlaid by stochastic laws. For instance, a simple static structure such as a crystal can be described by a short binary string hence has little amount of information. As Lin [
13] suggests, symmetric static structures (crystals) and nonsymmetrical static structures have different amounts of descriptive information.
Lin realizes the incompatibility of Shannon’s information theory in explaining spontaneous processes and suggests that the classical definition of entropy as a measure of disorder has been incorrectly used in the associated fields of science. Clearly, a static structure (not necessarily a crystal), which is a frozen dynamic structure, is in a more orderly state than a system of dynamic motion. But when comparing two static structures the symmetric one should be measured as having more order (less chaotic), being simpler and having less information content than the nonsymmetrical structure. As he remarks, this is not explained well by the classical (Shannon) definitions of entropy and information. According to these definitions, a more symmetric and ordered system is obtained by the introduction of additional information, i.e., by a reduction in entropy. This seems to contradict observed spontaneous processes (such as those mentioned above) which occur automatically without any external (information agent) intervention while still leading to the formation of simpler and more stable systems that have a higher degree of symmetry (and less information-content).
Lin’s approach to explaining this is to generalize the notion of entropy (although, this is not defined precisely) also for static (deterministic) objects, i.e., nonprobabilistic structures. He then postulates a third law of information theory which states that maximal static entropy (and zero information content) exists in a perfect crystal at zero absolute temperature. Together with the second law of information theory (which parallels the second law of thermodynamics) this forms the basis for explaining the above processes.
Lin has made important and deep contribution in making the connection between the concepts of entropy, simplicity, symmetry and similarity, but as he writes (on p. 373, [
12]), ”..it is more important to give an information content formula for static structures” and then remarks that to his knowledge there is no such formula.
In this paper we develop such formulation and introduce an alternate explanation to his notion of static entropy. Our approach is based on the area of algorithmic information theory which relates concepts of randomness and complexity of finite objects (since any finite object may be described by a finite binary sequence we henceforth refer to them simply as binary sequences).
We explain Lin’s principle of higher entropy—higher symmetry through the mathematical constructs of algorithmic information theory. We state a precise quantitative definition of the information content of an object (what Lin calls a static structure or solid) and then give statements about the relation between algorithmic complexity (this replaces Lin’s notion static entropy), information content (of an object such as a solid) and its stability (which Lin associates with symmetry).
Starting in the next section we introduce several concepts from this area.
2. Algorithmic complexity
Kolmogorov [
9] proposed to measure the conditional complexity of a finite object
x given a finite object
y by the length of the shortest binary sequence
p (a program for computing
x) which consists of 0s and 1s and which reconstructs
x given
y. Formally, this is defined as
where
l(
p) is the length of the sequence
p,
φ is a universal partial recursive function which acts as a description method, i.e., when provided with input (
p, y) it gives a specification for
x. The word universal means that the function
φ can emulate any Turing machine (hence any partial recursive function). One can view
φ as a universal computer that can interpret any programming language and accept any valid program
p. The Kolmogorov complexity of
x given
y as defined in (1) is the length of the shortest program that generates
x on this computer given
y as input. The special case of
y being the empty binary sequence gives the unconditional Kolmogorov complexity
K(
x). This has been later extended by [
4,
7] to the prefix-complexity which requires
p to be coded in a prefix-free format.
3. Algorithmic randomness
The notion of randomness or stochasticity of finite objects (binary sequences) aims to explain the intuitively clear notion that a sequence, whether finite or infinite, should be measured as being more unpredictable if it possess fewer regularities (patterns). This conceptualization underlies a fundamental notion in information theory and in the area known as algorithmic information theory which states that the existence of regularities underlying data necessarily implies information redundancy in the data (observations). This notion has become the basis of the well-known principle of Minimum Description Length (MDL) [
18] which was proposed as a computable approximation of Kolmogorov complexity and has since served as a powerful method for inductive inference. The MDL principle states that given a limited set of observed data the best explanation or model (hypothesis) is the one that permits the greatest compression of the data. That is, the more we are able to compress the data, the more we learn about the underlying regularities that generated the data.
The area known as
algorithmic randomness studies the relationship between complexity and stochasticity (the degree of unpredictability) of finite and infinite binary sequences [
3]. Algorithmic randomness was first considered by von Mises in 1919 who defined an infinite binary sequence
α of zeros and ones as ‘random’ if it is unbiased, i.e. if the frequency of zeros goes to 1
/2, and every subsequence of
α that we can extract using an ‘admissible’ selection rule (see
§4) is also not biased.
Von Mises never made completely precise what he meant by admissible selection rule. Church proposed a formal definition of such a rule to be a (total) computable process which, having read the first
n bits of an infinite binary sequence
α, decides if it wants to select the next bit or not, and then reads it (it is crucial that the decision to select the bit or not is made before reading the bit). The sequence of selected bits is the selected subsequence with respect to the selection rule. Kolmogorov and Loveland [
10,
15] argued that in Church’s definition the bits are read in order, which is too restrictive. They proposed a more permissive definition of an admissible selection rule as any (partial) computable process which, having read any
n bits of an infinite binary sequence
α, picks a bit that has not been read yet, decides whether it should be selected or not, and then reads it. When subsequences selected by such a selection rule pass the unbiasness test they are called Kolmogorov-Loveland stochastic (KL-stochastic for short).
It turns out that even with this improvement, KL-stochasticity is too weak a notion of randomness. Shen [
20] showed that there exists a KL-stochastic sequence all of whose prefixes contain more zeros than ones. Martin L
öf [
16] introduced a notion of randomness which is now considered by many as the most satisfactory notion of algorithmic randomness. Martin-L
öf’s definition says precisely which infinite binary sequences are random and which are not. The definition is probabilistically convincing in that it requires each random sequence to pass every algorithmically implementable statistical test of randomness. From the work of [
19] Martin-L
öf randomness can be characterized in terms of Kolmogorov complexity (1) of
α. An infinite binary sequence
is Martin-L
öf random if and only if there is a constant
c such that for all
n,
K(
α1,. . . ,
αn)
≥ n − c where
K is the prefix Kolmogorov complexity [
5].
4. Selection rule
In this section we describe the notion of a selection rule. As mentioned in the previous section this is a principal concept used as part of tests of randomness of sequences. In later sections we use this to develop a framework for explaining Lin’s third law.
An admissible
selection rule R is defined [
22] based on three partial recursive functions
f,
g and
h on
. Let
x =
x1, . . . ,
xn. The process of selection is recursive. It begins with an empty sequence ∅. The function
f is responsible for selecting possible candidate bits of
x as elements of the subsequence to be formed. The function
g examines the value of these bits and decides whether to include them in the subsequence. Thus
f does so according to the following definition:
f (∅) =
i1, and if at the current time
k a subsequence has already been selected which consists of elements
xi1 , . . . ,
xik then
f computes the index of the next element to be examined according to element
f (
xi1 , . . . ,
xik) =
i where
i ∉{
i1 ,. . . ,
ik}, i.e., the next element to be examined must not be one which has already been selected (notice that maybe
i < ij , 1
≤ j ≤ k, i.e., the selection rule can go backwards on
x). Next, the two-valued function
g selects this element
xi to be the next element of the constructed subsequence of
x if and only if
g(
xi1 , . . . ,
xik) = 1. The role of the two-valued function
h is to decide when this process must be terminated. This subsequence selection process terminates if
h(
xi1 , . . . ,
xik ) = 1 or
f (
xi1 , . . . ,
xik )
> n. Let
R(
x) denote the selected subsequence. By
K(
R|n) we mean the length of the shortest program computing the values of
f ,
g and
h given
n.
6. Biasness
From the previous sections we know that there are two principal measures related to the information content in a finite sequence
x, stochasticity (unpredictability) and chaoticity (complexity). An infinitely long binary sequence is regarded random if it satisfies the principle of stability of the frequency of 1s for any of its subsequences that are obtained by an admissible selection rule [
8,
10].
Kolmogorov [
9] showed that the stochasticity of a finite binary sequence
x may be precisely expressed by the deviation of the frequency of ones from some 0
< p < 1, for any subsequence of
x selected by an admissible selection rule
R of finite complexity
K(
R|n). The chaoticity of
x is the opposite of its randomness deficiency, i.e., it is large if its Kolmogorov complexity is close to its length
n. The works of [
1,
2,
9,
22] relate this chaoticity to stochasticity. In [
1,
2] it is shown that chaoticity implies stochasticity. This can be seen from the following relationship (with
p = 1
/2):
where for a binary sequence
s, #ones(
s) denotes the number of 1s in
s,
ν(
s) = #ones(
s)
/l(
s) represents the frequency of 1s in
s,
l(
R(
x)) the length of the subsequence selected by
R and
c > 0 is some absolute constant.
From this we see that as the chaoticity of
x grows (the randomness deficiency decreases) the stochasticity of the selected subsequence grows, i.e., the bias from 1
/2 decreases. The information content of the selection rule, namely
K(
R|n), has a direct effect on this relationship: the lower
K(
R|n) is the stronger the stability (i.e., the smaller the deviation of the frequency of 1s from 1
/2). In [
6] the other direction is proved which shows that stochasticity implies chaoticity.
7. Interpreting a static structure as a selection rule
In this section we apply the above theory to explain Lin’s principle of symmetry, static entropy and stability whose key features and relationship are summarized again here below:
higher symmetry—higher static entropy (Lin’s third law of information theory)
higher symmetry—higher stability (the most symmetric microstate will be the most stable static structure)
higher static entropy—higher loss of information (a system with high information-content is unstable, spontaneous phase separation is accompanied by an information loss)
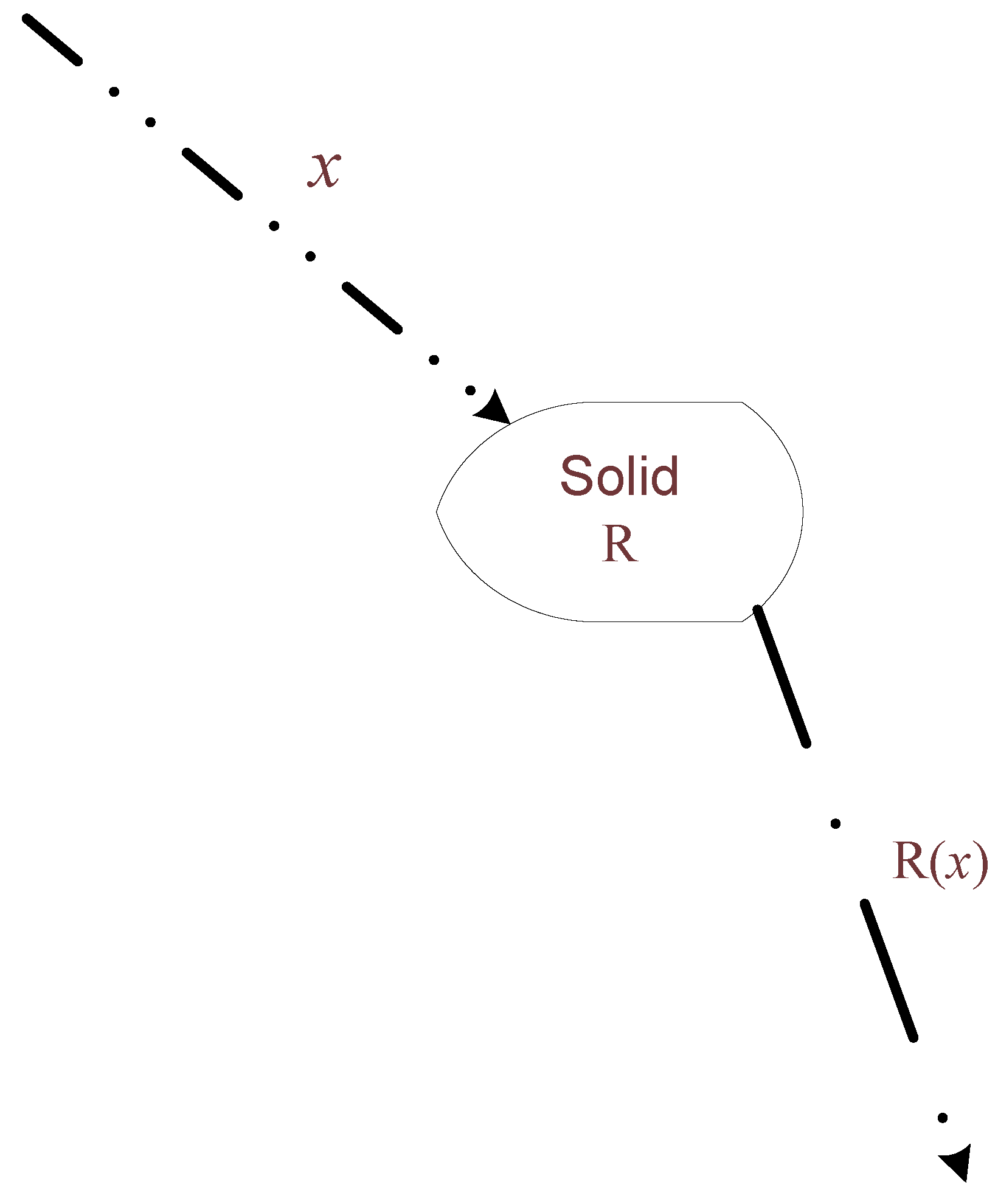
Consider a solid which represents a static structure in which information is registered [
12]. The surrounding universe consists of a dynamic system of particles randomly hitting the solid, some are deflected and some pass through. Let us represent this as a binary sequence
x with
xi = 1 representing a particle hitting the solid and
xi = 0 indicating the absence of a particle at discrete time
i. This surrounding universe is as close to what can be considered as perfect (or true) source of randomness. Thus the randomness deficiency of
x is at its minimum. We associate with the solid a selection rule
R which acts by realizing an algorithm of complexity
K(
R) which selects certain bits from
x and decides whether to let the bit be in the output subsequence
R(
x) of
x (
Figure 1). Note that the formed subsequence
R(
x) may consist of not only 1s but also 0s since discrete time
i (which indexes the bits) keeps increasing also when no particle hits the solid and hence when no particle emerges from the back surface of the solid.
Figure 1.
Interaction of solid with surrounding space.
Figure 1.
Interaction of solid with surrounding space.
The selection mechanism of particular bits of the input sequence
x by the solid (similar to the way
f is defined for a selection rule in
§4) is due to the solid’s complex response to the presence of a sequence of particles hitting it. For instance, a solid’s dielectric constants or material nonhomogeneity cause a nonlinear response to particle bombardment, e.g., photoconductive solid materials bombarded by photon particles [
17] and superconductive thin films hit by ions [
11] exhibit transient responses. This is analogous to the impulse response of a non-perfect filter in communication systems. Materials science applications involving pulsed beams show that the time dependent response of a solid to a high energy ion beam is described by complex hydrodynamic codes [
21]. Consider a random electronic signal consisting of a sequence
x of binary pulses which inputs to an electronic switching device with a transient response governed by time constants. Then for certain segments of
x where the pulses frequency is high the device will not manage to track exactly every bit change in the input sequence
x and as a result its output will correspond only to a certain subsequence of
x. This inability to track the input sequence in a precise way implies that the device (and similarly a solid acting on a random sequence of particles) effectively selects certain bits from
x and ‘decides’ which to pass through.
A simple solid is one whose information content is small. Its selection behavior is of low complexity K(R) since it can be described by a more concise time-response model (shorter ‘program’). We assert that representing the complexity of a static structure by the Kolmogorov complexity of its corresponding selection rule R allows to make Lin’s qualitative notion of static entropy more robust. Lin’s notion of stability can alternatively be represented by the stability of the frequency of 1s in the selected subsequence R(x). Provided that x has a small randomness deficiency δ(x|n) it follows from (2) that for a solid with low information content (small K(R|n)) the deviation of the frequency of 1s from 1/2 will be small. This means that the frequency stability is large. We assert that this notion of stability corresponds with Lin’s notion of physical stability of the system, i.e., the stability of a static structure.
A more complex static structure (solid R with large K(R|n)) leads to a higher deviation, i.e., lower stability, of the frequency of 1s from 1/2 in the selected subsequence R(x). We assert that this is in correspondence with Lin’s notion of instability of a system with high information content.
Lin’s third law states that any spontaneous process (irreversible) tends to produce a structure of a higher static entropy which in his words ”minimizes information and maximizes symmetry”. According to our framework, this third law is explained as follows: over the course of time (and provided there are no external intervention or constraints) a solid structure will eventually not be able to maintain its ‘interference’ with the perfect randomness of its surrounding universe (viewed here as a selection rule, interference means that the selected subsequence has a frequency of 1s which is biased away from 1/2). At some point, the static structure cannot maintain its resistance to randomness and becomes algorithmically less complex and thereby moves into a more stable state.
In summary, our explanation of Lin’s third law is as follows: static structures (compared to dynamic systems) are like points of interference in space of perfect randomness. They resist randomness of the surrounding universe and as a result are less stable. Static structures cannot maintain their complexity indefinitely. Eventually, they undergo change in the direction of being less algorithmically complex and this makes their interference with the randomness of the surrounding universe weaker. As a result they become more stable.
In agreement with Lin’s assertion that a perfect crystal has zero information content and maximal static entropy, we assert that given any random sequence x of length n then the selection rule R associated with Lin’s crystal has a small (constant with n) Kolmogorov complexity K(R|n) and the selected subsequence R(x) (which is also random) has a maximum stability of the frequency of 1s.