Gibbs’ Paradox and the Definition of Entropy
Abstract
:1. Introduction
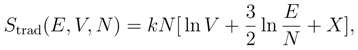
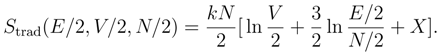
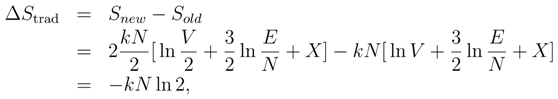
2. Boltzmann’s definition of the entropy
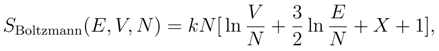
3. Gibbs’ Paradox and the entropy of mixing
4. Conclusions
References
- Gibbs, J. W. On the Equilibrium of Heterogeneous Substances. Transactions of the Connecticut Academy 1873, 3, 108–248, 343–524. [Google Scholar] [CrossRef]
- Gibbs, J. W. The Collected Works of J. W. Gibbs; Yale University Press, 1948; Vol. 1. [Google Scholar]
- Gibbs, J. W. Elementary Principles of Statistical Mechanics; Yale University Press: New Haven, 1902; Reprinted by (Dover, New York, 1960); pp. 206–207. [Google Scholar]
- Pathria, R. K. Statistical Mechanics, 2nd ed.; Butterworth-Heinemann: Boston, 1996; pp. 22–26, See especially Eq. (1a), which agrees with Eq. 1 in this paper if the temperature is replaced by the energy as a variable. [Google Scholar]
- Landau, L. D.; Lifshitz, E. M. Statistical Physics; Pergamon Press: New York, 1980; pp. 24–25. [Google Scholar]
- Reif, F. Fundamentals of Statistical and Thermal Physics; McGraw-Hill: New York, 1965; pp. 243–245, This book and some others use a definition of the partition function that also leads to the traditional expression for the entropy. [Google Scholar]
- Everett, D. H. Basic Principles of Colloid Science; Royal Society of Chemistry: London, 1988. [Google Scholar]
- Boltzmann, L. Über die Beziehung zwischen dem zweiten Hauptsatze der mechanischen Wärmetheorie und der Wahrscheinlichkeitsrechnung respektive den Sätzen über das Wärmegleichgewicht. Wien. Ber. 1877, 76, 373–435, Reprinted in Wissenschaftliche Abhandlungen von Ludwig Boltzmann, Vol. II; Chelsea: New York, 1968; pp. 164–223. [Google Scholar]
- Swendsen, R. H. Statistical mechanics of colloids and Boltzmann’s definition of the entropy. Am. J. Phys. 2006, 74, 187–190. [Google Scholar] [CrossRef]
- Swendsen, R. H. Statistical mechanics of classical systems of distinguishable particles. J. Stat. Phys. 2002, 107, 1143–1165. [Google Scholar] [CrossRef]
- Planck, M. Über das Gesetz der Energieverteilung im Normalspektrum. Drudes Annalen 1901, 553–562, Reprinted in Ostwalds Klassiker der exakten Wissenschaften, Band 206, Die Ableitung der Strahlungsgesetze, pp.65–74. The equation appears with an arbitrary additive constant on p. 68 of the reprinted text. [Google Scholar] [CrossRef]
- Planck, M. Theorie der Wärmestrahlung; J. A. Barth: Leipzig, 1906; Translated into English by Morton Masius in M. Planck, The Theory of Heat Radiation; Dover: New York, 1991; p. 119. [Google Scholar]
- Jaynes, E. T. The Gibbs Paradox. In Maximum-Entropy and Bayesian Methods; Erickson, G., Neudorfer, P., Smith, C. R., Eds.; Kluwer: Dordrecht, 1992; pp. 1–22. [Google Scholar]
- Ben-Naim, A. On the So-Called Gibbs Paradox, and on the Real Paradox. Entropy 2007, 9, 133–136. [Google Scholar] [CrossRef] [Green Version]
© 2008 by MDPI (http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
Swendsen, R.H. Gibbs’ Paradox and the Definition of Entropy. Entropy 2008, 10, 15-18. https://doi.org/10.3390/entropy-e10010015
Swendsen RH. Gibbs’ Paradox and the Definition of Entropy. Entropy. 2008; 10(1):15-18. https://doi.org/10.3390/entropy-e10010015
Chicago/Turabian StyleSwendsen, Robert H. 2008. "Gibbs’ Paradox and the Definition of Entropy" Entropy 10, no. 1: 15-18. https://doi.org/10.3390/entropy-e10010015
APA StyleSwendsen, R. H. (2008). Gibbs’ Paradox and the Definition of Entropy. Entropy, 10(1), 15-18. https://doi.org/10.3390/entropy-e10010015



