Evaluating Model Fit in Two-Level Mokken Scale Analysis
Abstract
:1. Introduction
2. Model-Fit Investigation
2.1. Single-Level NIRT Models
2.2. Two-Level NIRT Models
2.3. Model Fit of Single-Level NIRT Models
2.3.1. Testing Local Independence
- for all ;
- for all and all values of k; and
- for all , and all values of y.
2.3.2. Testing Monotonicity
2.3.3. Testing Invariant Item Ordering
2.4. Model Fit of Two-Level NIRT Models
2.4.1. Testing Local Independence at Level 2
2.4.2. Testing Monotonicity at Level 2
2.4.3. Testing Invariant Item Ordering
3. Method
3.1. Data Generation Strategy
3.2. Study Design
3.2.1. Independent Variables
3.2.2. Dependent Variables
3.3. Hypotheses
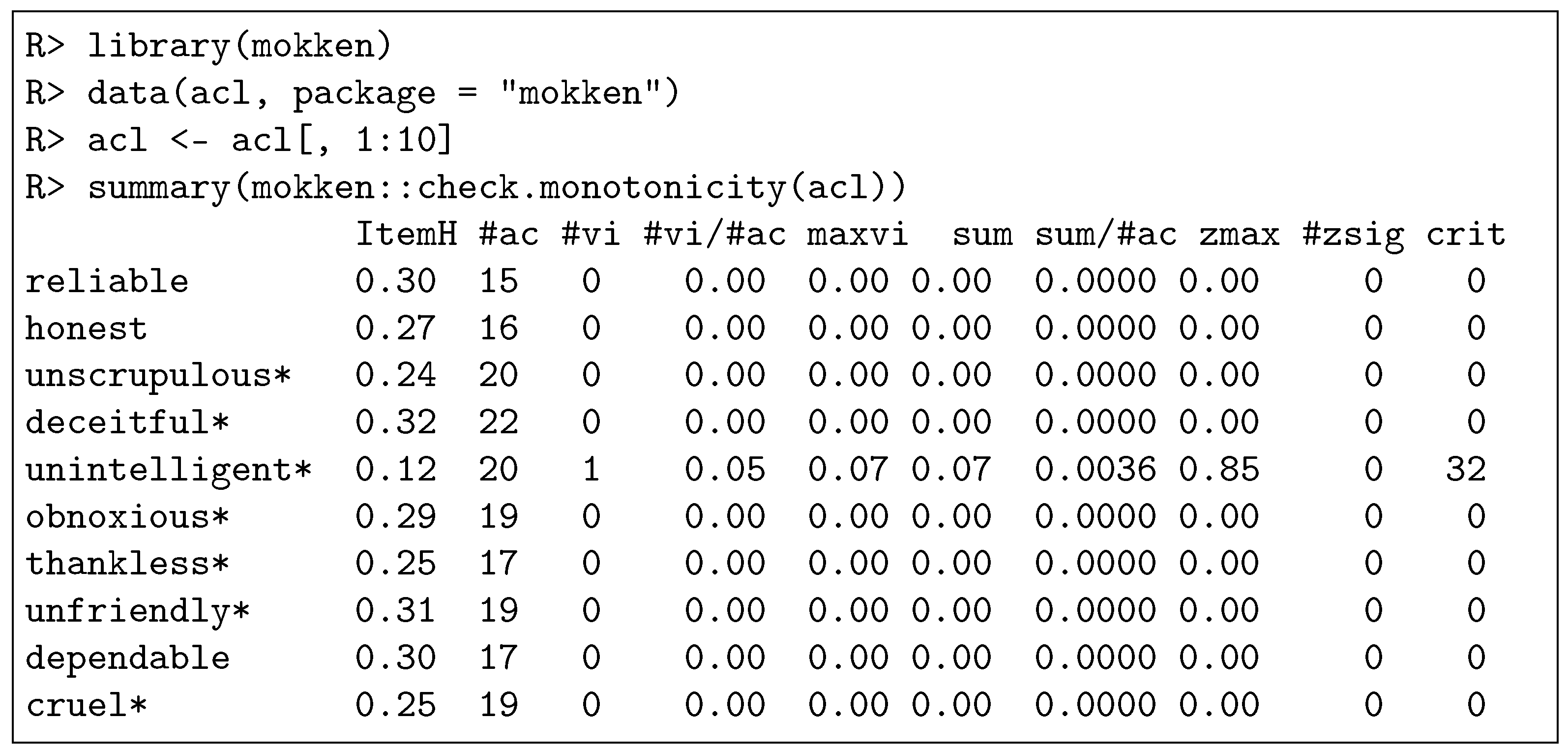
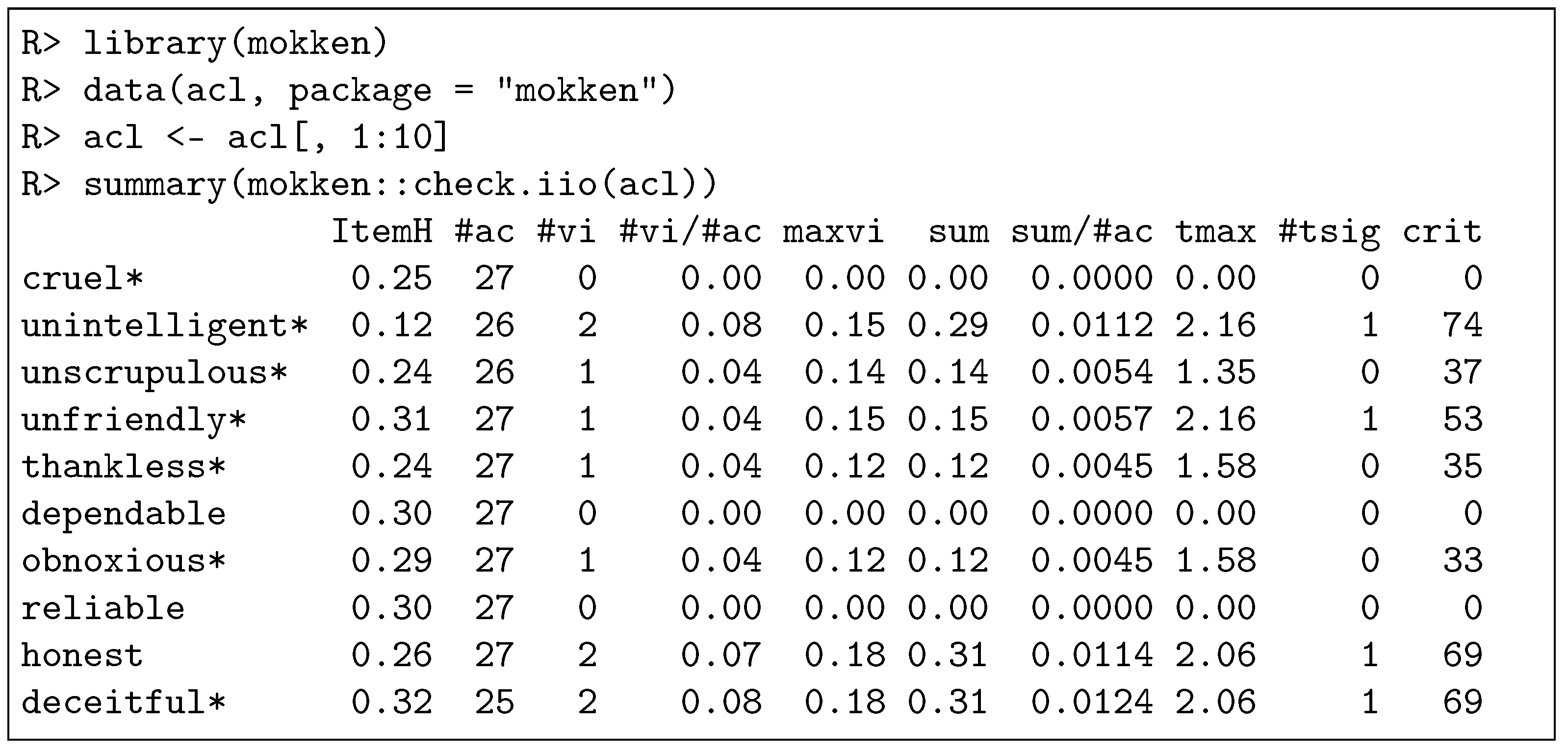
3.4. Statistical Analyses
- check.monotonicity(X, level.two.var = clusters)
- check.iio(X, level.two.var = clusters)
4. Results
4.1. Manifest Monotonicity
4.2. Manifest Invariant Item Ordering
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DMM | Double monotonicity model |
| IIO | Invariant item ordering |
| IRF | Item response function |
| IRT | Item response theory |
| ISRF | Item step response function |
| MHM | Monotone homogeneity model |
| MSA | Mokken scale analysis |
| NIRT | Nonparametric item response theory |
Appendix A
References
- Mokken, R.J. A Theory and Procedure of Scale Analysis; Mouton: The Hague, The Netherlands, 1971. [Google Scholar]
- Sijtsma, K.; Molenaar, I.W. Introduction to Nonparametric Item Response Theory; Sage: Thousand Oaks, CA, USA, 2002. [Google Scholar]
- Sijtsma, K.; Van der Ark, L.A. A tutorial on how to do a Mokken scale analysis on your test and questionnaire data. Br. J. Math. Stat. Psychol. 2017, 70, 137–158. [Google Scholar] [CrossRef]
- Van Schuur, W.H. Mokken scale analysis: Between the Guttman scale and parametric item response theory. Political Anal. 2003, 11, 139–163. [Google Scholar] [CrossRef] [Green Version]
- Wind, S.A. An instructional module on Mokken scale analysis. Educ. Meas. Issues Pract. 2017, 36, 50–66. [Google Scholar] [CrossRef]
- Loevinger, J. The technique of homogeneous tests compared with some aspects of “scale analysis" and factor analysis. Psychol. Bull. 1948, 45, 507–529. [Google Scholar] [CrossRef]
- Kuijpers, R.E.; Van der Ark, L.A.; Croon, M.A. Standard errors and confidence intervals for scalability coefficients in Mokken scale analysis using marginal models. Sociol. Methodol. 2013, 43, 42–69. [Google Scholar] [CrossRef]
- Koopman, L.; Zijlstra, B.J.H.; Van der Ark, L.A. Range-preserving confidence intervals and significance tests for scalability coefficients in Mokken scale analysis. In Quantitative Psychology: Proceedings of the 85th Annual Meeting of the Psychometric Society, Virtual; Wiberg, M., Molenaar, D., González, J., Böckenholt, U., Kim, J.S., Eds.; Springer: Cham, Switzerland, 2021; pp. 175–185. [Google Scholar]
- Van der Ark, L.A.; Croon, M.A.; Sijtsma, K. Mokken scale analysis for dichotomous items using marginal models. Psychometrika 2008, 73, 183–208. [Google Scholar] [CrossRef] [Green Version]
- Hemker, B.T.; Sijtsma, K.; Molenaar, I.W. Selection of unidimensional scales from a multidimensional itembank in the polytomous Mokken IRT model. Appl. Psychol. Meas. 1995, 19, 337–352. [Google Scholar] [CrossRef] [Green Version]
- Straat, J.H.; Van der Ark, L.A.; Sijtsma, K. Comparing optimization algorithms for item selection in Mokken scale analysis. J. Classif. 2013, 30, 75–99. [Google Scholar] [CrossRef]
- Brusco, M.J.; Köhn, H.F.; Steinley, D. An exact method for partitioning dichotomous items within the framework of the monotone homogeneity model. Psychometrika 2015, 80, 949–967. [Google Scholar] [CrossRef]
- Koopman, L.; Zijlstra, B.J.H.; Van der Ark, L.A. A two-step, test-guided Mokken scale analysis, for nonclustered and clustered data. Qual. Life Res. 2022, 31, 25–36. [Google Scholar] [CrossRef]
- Holland, P.W.; Rosenbaum, P.R. Conditional association and unidimensionality in monotone latent variable models. Ann. Stat. 1986, 14, 1523–1543. [Google Scholar] [CrossRef]
- Hemker, B.T.; Sijtsma, K.; Molenaar, I.W.; Junker, B.W. Stochastic ordering using the latent trait and the sum score in polytomous IRT models. Psychometrika 1997, 62, 331–347. [Google Scholar] [CrossRef] [Green Version]
- Grayson, D.A. Two-group classification in latent trait theory: Scores with monotone likelihood ratio. Psychometrika 1988, 53, 383–392. [Google Scholar] [CrossRef]
- Van der Ark, L.A.; Bergsma, W.P. A note on stochastic ordering of the latent trait using the sum of polytomous item scores. Psychometrika 2010, 75, 272–279. [Google Scholar] [CrossRef] [Green Version]
- Rasch, G. Probabilistic Models for Some Intelligence and Attainment Tests; Nielsen & Lydiche: Copenhagen, Denmark, 1960. [Google Scholar]
- Birnbaum, A. Some Latent Trait Models and Their Use in Inferring an Examinee’s Ability. In Statistical Theories of Mental Test Scores; Lord, F.M., Novick, M.R., Eds.; Addison-Wesley: Reading, MA, USA, 1968. [Google Scholar]
- Samejima, F. Estimation of Latent Ability Using a Response Pattern of Graded Scores; (Psychometrika monograph supplement No. 17); Psychometric Society: Richmond, VA, USA, 1969. [Google Scholar]
- Masters, G.N. A Rasch model for partial credit scoring. Psychometrika 1982, 47, 149–174. [Google Scholar] [CrossRef]
- Tutz, G. Sequential item response models with an ordered response. Br. J. Math. Stat. Psychol. 1990, 43, 39–55. [Google Scholar] [CrossRef]
- Van der Ark, L.A. Relationships and properties of polytomous item response theory models. Appl. Psychol. Meas. 2001, 25, 273–282. [Google Scholar] [CrossRef] [Green Version]
- Kaufman, A.S.; Raiford, S.E.; Coalson, D.L. Intelligent Testing with the WISC-V; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Fraser, B.; McRobbie, C.; Fisher, D. Development, validation and use of personal and class forms of a new classroom environment questionnaire. In Proceedings of the Western Australian Institute for Educational Research Forum 1996; Wild, M., Ed.; WAIER: Perth, WA, Australia, 1996. [Google Scholar]
- Robinson, W.S. Ecological Correlations and the Behavior of Individuals. Am. Sociol. Rev. 1950, 15, 351–357. [Google Scholar] [CrossRef]
- Snijders, T.A.B.; Bosker, R.J. Multilevel Analysis: An Introduction to Basic and Advanced Multilevel Modeling, 2nd ed.; Sage: Thousand Oaks, CA, USA, 2012. [Google Scholar]
- Snijders, T.A.B. Two-level non-parametric scaling for dichotomous data. In Essays on Item Response Theory; Boomsma, A., van Duijn, M.A.J., Snijders, T.A.B., Eds.; Springer: New York, NY, USA, 2001; pp. 319–338. [Google Scholar]
- Crişan, D.R.; Van de Pol, J.E.; Van der Ark, L.A. Scalability Coefficients for Two-Level Polytomous Item Scores: An Introduction and an Application. In Quantitative Psychology Research, Proceedings of the 80th Annual Meeting of the Psychometric Society, Beijing, China, 12–16 July 2015; van der Ark, L.A., Bolt, D.M., Wang, W.C., Douglas, J.A., Wiberg, M., Eds.; Springer: Cham, Switzerland, 2016; pp. 139–153. [Google Scholar]
- Koopman, L.; Zijlstra, B.J.H.; Van der Ark, L.A. Standard errors of two-level scalability coefficients. Br. J. Math. Stat. Psychol. 2020, 73, 213–236. [Google Scholar] [CrossRef]
- Koopman, L.; Zijlstra, B.J.H.; De Rooij, M.; Van der Ark, L.A. Bias of two-level scalability coefficients and their standard errors. Appl. Psychol. Meas. 2020, 44, 197–214. [Google Scholar] [CrossRef]
- Koopman, L.; Zijlstra, B.J.H.; Van der Ark, L.A. Assumptions and Properties of Two-Level Nonparametric Item Response Theory Models. Submitt. Publ. 2023. [Google Scholar]
- Van der Ark, L.A. Mokken Scale Analysis in R. J. Stat. Softw. 2007, 20, 1–19. [Google Scholar]
- Van der Ark, L.A. New Developments in Mokken Scale Analysis in R. J. Stat. Softw. 2012, 48, 1–27. [Google Scholar]
- Reckase, M.D. Multidimensional Item Response Theory; Springer: Dordrecht, The Netherlands, 2009. [Google Scholar]
- Kelderman, H. Loglinear Rasch model tests. Psychometrika 1984, 49, 223–245. [Google Scholar] [CrossRef] [Green Version]
- Andrich, D. A rating formulation for ordered response categories. Psychometrika 1978, 43, 561–573. [Google Scholar] [CrossRef]
- Sijtsma, K.; Hemker, B.T. Nonparametric polytomous IRT models for invariant item ordering, with results for parametric models. Psychometrika 1998, 63, 183–200. [Google Scholar] [CrossRef] [Green Version]
- Ligtvoet, R.; Van der Ark, L.A.; Bergsma, W.P.; Sijtsma, K. Polytomous latent scales for the investigation of the ordering of items. Psychometrika 2011, 76, 200–216. [Google Scholar] [CrossRef] [Green Version]
- Rosenbaum, P.R. Probability inequalities for latent scales. Br. J. Math. Stat. Psychol. 1987, 40, 157–168. [Google Scholar] [CrossRef]
- Conners, C.K.; Sitarenios, G.; Parker, J.D.A.; Epstein, J.N. The revised Conners’ Parent Rating Scale (CPRS-R): Factor structure, reliability, and criterion validity. J. Abnorm. Child Psychol. 1998, 26, 257–268. [Google Scholar] [CrossRef]
- Straat, J.H.; Van der Ark, L.A.; Sijtsma, K. Using conditional association to identify locally independent item sets. Methodology 2016, 12, 117–123. [Google Scholar] [CrossRef]
- Ellis, J.L. An inequality for correlations in unidimensional monotone latent variable models for binary variables. Psychometrika 2014, 79, 303–316. [Google Scholar] [CrossRef]
- Crişan, D.R. Specificity and Sensitivity of Two Lower Bound Estimates for the Scalability Coefficients in Mokken Scale Analysis: A Simulation Study. In Internship Report; University of Amsterdam: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Junker, B.W. Conditional association, essential independence and monotone unidimensional item response models. Ann. Stat. 1993, 21, 1359–1378. [Google Scholar] [CrossRef]
- Junker, B.W.; Sijtsma, K. Latent and manifest monotonicity in item response models. Appl. Psychol. Meas. 2000, 24, 65–81. [Google Scholar] [CrossRef]
- Molenaar, I.W.; Sijtsma, K. User’s Manual MSP5 for Windows; IEC ProGAMMA: Groningen, The Netherlands, 2000. [Google Scholar]
- Ligtvoet, R.; Van der Ark, L.A.; Te Marvelde, J.M.; Sijtsma, K. Investigating an invariant item ordering for polytomously scored items. Educ. Psychol. Meas. 2010, 70, 578–595. [Google Scholar] [CrossRef] [Green Version]
- Crişan, D.R.; Tendeiro, J.N.; Meijer, R.R. The Crit coefficient in Mokken scale analysis: A simulation study and an application in quality-of-life research. Qual. Life Res. 2022, 31, 49–59. [Google Scholar] [CrossRef]
- Koopman, L. Effect of Within-Group Dependency on Fit Statistics in Mokken Scale Analysis in the Presence of Two-Level Test Data. In Quantitative Psychology: Proceedings of the 87th Annual Meeting of the Psychometric Society, Bologna, Italy, 11–15 July 2022; Wiberg, M., Molenaar, D., González, J., Kim, J.S., Eds.; Springer: Cham, Switzerland, 2022; in press. [Google Scholar]
- Morris, T.P.; White, I.R.; Crowther, M.J. Using simulation studies to evaluate statistical methods. Stat. Med. 2019, 38, 2074–2102. [Google Scholar] [CrossRef] [Green Version]
- Straat, J.H.; Van der Ark, L.A.; Sijtsma, K. Minimum sample size requirements for Mokken scale analysis. Educ. Psychol. Meas. 2014, 74, 809–822. [Google Scholar] [CrossRef]
- Watson, R.; Egberink, I.J.L.; Kirke, L.; Tendeiro, J.N.; Doyle, F. What are the minimal sample size requirements for Mokken scaling? An empirical example with the Warwick-Edinburgh Mental Well-Being Scale. Health Psychol. Behav. Med. 2018, 6, 203–213. [Google Scholar] [CrossRef] [Green Version]
- Wind, S.A. Identifying problematic item characteristics with small samples using Mokken scale analysis. Educ. Psychol. Meas. 2022, 82, 747–756. [Google Scholar] [CrossRef]
- Stapleton, L.M.; Yang, J.S.; Hancock, G.R. Construct meaning in multilevel settings. J. Educ. Behav. Stat. 2016, 41, 481–520. [Google Scholar] [CrossRef]



| Indicator | Violation | S | Level 1 | Level 2 | |||
|---|---|---|---|---|---|---|---|
| #vi/#ac | None | 50 | 0.003 | 0.005 | 0.010 | 0.015 | 0.032 |
| 200 | 0.003 | 0.004 | 0.006 | 0.012 | 0.019 | ||
| #zsig | None | 50 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 |
| 200 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| Indicator | Violation | S | Level 1 | Level 2 | |||
|---|---|---|---|---|---|---|---|
| #vi/#ac | Small | 50 | 0.334 | 0.511 | 0.443 | 0.297 | 0.246 |
| 200 | 0.325 | 0.477 | 0.398 | 0.285 | 0.241 | ||
| Large | 50 | 0.726 | 0.737 | 0.731 | 0.701 | 0.567 | |
| 200 | 0.731 | 0.751 | 0.752 | 0.729 | 0.625 | ||
| #zsig | Small | 50 | 1.466 | 0.000 | 0.000 | 0.000 | 0.000 |
| 200 | 1.354 | 0.255 | 0.017 | 0.000 | 0.001 | ||
| Large | 50 | 7.677 | 0.111 | 0.000 | 0.000 | 0.000 | |
| 200 | 7.803 | 4.847 | 2.491 | 0.335 | 0.021 | ||
| Indicator | Violation | S | Level 1 | Level 2 | |||
|---|---|---|---|---|---|---|---|
| #vi/#ac | None | 50 | 0.007 | 0.009 | 0.010 | 0.010 | 0.008 |
| 200 | 0.006 | 0.007 | 0.006 | 0.007 | 0.007 | ||
| #tsig | None | 50 | 0.000 | 0.001 | 0.003 | 0.002 | 0.004 |
| 200 | 0.000 | 0.001 | 0.003 | 0.000 | 0.001 | ||
| Indicator | Violation | S | Level 1 | Level 2 | |||
|---|---|---|---|---|---|---|---|
| #vi/#ac | Small | 50 | 0.322 | 0.376 | 0.344 | 0.309 | 0.251 |
| 200 | 0.325 | 0.377 | 0.342 | 0.305 | 0.257 | ||
| Large | 50 | 0.507 | 0.510 | 0.488 | 0.468 | 0.408 | |
| 200 | 0.520 | 0.524 | 0.521 | 0.496 | 0.449 | ||
| #tsig | Small | 50 | 0.380 | 0.671 | 0.556 | 0.379 | 0.189 |
| 200 | 0.384 | 0.668 | 0.534 | 0.350 | 0.221 | ||
| Large | 50 | 1.658 | 1.961 | 1.757 | 1.505 | 1.011 | |
| 200 | 1.694 | 1.901 | 1.786 | 1.526 | 1.202 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koopman, L.; Zijlstra, B.J.H.; Van der Ark, L.A. Evaluating Model Fit in Two-Level Mokken Scale Analysis. Psych 2023, 5, 847-865. https://doi.org/10.3390/psych5030056
Koopman L, Zijlstra BJH, Van der Ark LA. Evaluating Model Fit in Two-Level Mokken Scale Analysis. Psych. 2023; 5(3):847-865. https://doi.org/10.3390/psych5030056
Chicago/Turabian StyleKoopman, Letty, Bonne J. H. Zijlstra, and L. Andries Van der Ark. 2023. "Evaluating Model Fit in Two-Level Mokken Scale Analysis" Psych 5, no. 3: 847-865. https://doi.org/10.3390/psych5030056





