Abstract
Recent attempts at searching for new materials have revealed a large class of materials that show topological behaviors with unusual physical properties and potential applications leading to enthralling discoveries both theoretically and experimentally. We computationally predict new three-dimensional topological compounds of space group 139(I/4mmm). After conducting a full volume optimization process by allowing the rearrangement of atomic positions and lattice parameters, the first-principles calculation with a generalized gradient approximation is utilized to identify multiple Dirac-type crossings around X and P symmetric points near Fermi energy. Importantly, the band inversion at point P is recognized. Further, we investigate the compound for topological crystalline insulating behavior by conducting surface state calculation and by investigating gapping behavior by increasing lattice parameters. Additionally, we perform formation energy, elastic properties, and phonon modes calculations to verify the structural, mechanical, and dynamical stability of the compounds. Therefore, we suggest compounds for further investigation and experimental realization.
1. Introduction
Following the discovery of a two-dimensional topological insulating phase in graphene with a significant effect of spin–orbit coupling (SOC) [1,2], rigorous efforts have been committed to exploring new topological materials. Among them, the identification of topological insulators (TIs) and topological semimetals (TSMs) with unusual physical properties and potential applications lead to new theoretical and experimental discoveries. TIs consist of a bulk insulating gap and gap-less conducting surface states that form a Dirac point [3,4] while topological semimetals (Dirac semimetals, Weyl semimetals, and nodal line semimetals) exhibit gapless bulk states and band crossings in momentum space which are inverted beyond the crossing point (or line) [5,6,7] protected by topology and symmetry.
Dirac semimetal behavior was first predicted and then realized in NaBi and CdAs [8,9,10,11,12,13,14]. Weyl semimetal behavior was predicted and realized in TaAs [5,15,16,17,18,19,20]. Nodal line semimetal behavior was predicted in CuPdN, CaP, CaP, PbO, CaAg, TiB, CaAgAs, ZrB, SrSi [21,22,23,24,25,26,27,28,29] and experimentally realized in , , , ZrSiSe, ZrSiTe, HfSiS, and ZrSnTe [18,30,31,32,33,34,35,36,37]. The gapless surface states across the band gap characterized by a topological invariant are topologically protected by time-reversal symmetry [3,4,38,39]. The binary alloys BiSe, BiTe, and SbTe that hold topological surface states are identified as strong TIs [40,41,42]. Topological crystalline insulators (TCIs) originated as a counterpart of topological insulators without the significant effect of SOC. The crystal symmetries in TCIs play a vital role in the topology of the bands showing gapless surface states across the insulating phase [39,43,44,45,46,47,48]. The TCI phase was first theoretically predicted and experimentally realized by angle-resolved photoemission spectroscopy in SnTe, PbSnSe, and PbSnTe [43]. Additionally, the SnS, SeTe, CaAs family and antiperovskites have also been reported to be TCIs [49,50,51,52,53]. Additionally, PbSe, PbTe, and PbS are predicted to be TCIs with a suitable combination of applied pressure or strain the Ref. [54]. The surface states of TCIs against the magnetic field strength seem to be more powerful than that of the TIs due to the mirror symmetry preservation without preserving the time reversal, but it may be ample to break the mirror symmetry and be a trivial insulator [46,55]. Therefore, there are potential drawbacks with the crystalline protection of TCIs [20,43,49,50,51,53], but it is desirable to find new topological materials [56,57,58,59,60,61] with pronounced transport properties and a wide range of controllability and functionalities for growing potential applications: quantum computing and spintronic devices.
In this work, a detailed study of electronic band structures and density of states (DOS) of new ternary BZn (X = Ir, Rh, Co) compounds in the tetragonal crystal structure of symmorphic space group 139 [I4/mmm] is presented. To the best of our knowledge, these compounds have not yet been reported either experimentally or theoretically in detail. In this paper, we report calculated electronic band structures of BZn after completing the full volume optimization process by allowing the rearrangement of atomic positions and lattice parameters to minimize the energy. We predict the formation of multiple type I Dirac crossings around X and P points on the Brillouin zone (BZ) near Fermi energy. With the careful investigation of electronic band structures and DOS of three compounds with and without the spin–orbit coupling (SOC), topological features are identified and discussed in detail. Further, we theoretically demonstrate that BZn has a possible signature of topological crystalline insulating features. Additionally, elastic constants and formation energy calculations are performed to verify the mechanical and structural stability of the new compounds. Further, the dynamical stability of compounds is assured by conducting phonon mode calculations.
2. Computational Method
The first-principle density functional theory (DFT) calculation method implemented on the Quantum ESPRESSO (QE) simulation package [62,63] was performed. The plane wave pseudo-potential formulated with generalized gradient approximation (GGA) and the Perdew–Burke–Ernzerhof (PBE) scheme was employed with the ultra-soft pseudo-potentials from PSlibrary, including fully relativistic ultra-soft pseudo-potentials for SOC [64,65,66,67,68,69]. The k-mesh of 20 × 20 × 20, kinetic energy cutoff for wave functions of 80 Ry, and kinetic energy cutoff for charge density and potential of 480 Ry were held to receive extreme convergence of energy and charge to enhance the accuracy of the simulation. Additionally, the WEIN2K simulation package [70,71] with PBE pseudo-potentials and a plane-wave basis set with GGA were used to compare and verify the QE results. A phonopy software package interfaced with QE under harmonic approximation was used to calculate the phonon spectrum, [72] and ElaStic software package cooperated with QE was used to calculate the full second-order elastic stiffness tensor [73]. The crystal momentum in units of has been used throughout the discussion unless otherwise specified.
3. Results and Discussion
3.1. Crystal Structure
Electron configurations of B, Zn, Ir, Rh, and Co are [He]2 2, [Ar]3 4, [Xe]4 5 6, [Kr] 4 5 and, [Ar]3 4 respectively. The B-p orbitals, X(Ir, Rh, Co)-d orbitals, and Rh-s orbitals are not fully occupied. The BZn (X = Ir, Rh, Co) compounds are structured theoretically as a tetragonal crystal structure of space group 139 [I4/mmm], which belongs to the centrosymmetric symmorphic space group.
The BZn structure is shown in Figure 1 by denoting Zn, B, and X in blue-, green-, and red-colored spheres, respectively. The arrangement of atoms for the Zn1, X1, and B1 layers is labeled as top–down views. The first BZ of the structure is shown in Figure 1b with the high symmetric points and the (0, 0, 0) point located at the center. The (001) surface BZ is shown in labeling with , , and including surface BZ at the center.
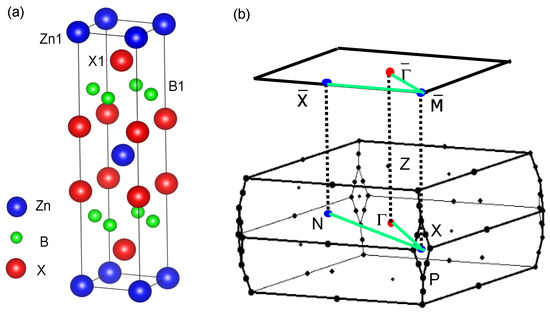
Figure 1.
(Color online) Crystal structure and BZ of the BZn compound. (a) Shows a tetragonal crystal structure of a layered pattern. The blue, green, and red solid spheres denote the Zn, B, and X atoms, respectively. The arrangement of atoms for each layer (Zn1, X1, and B1) is noted as top–down views. (b) Shows the first BZ by displaying high symmetry points of the BZ (black dots) with labeling (0, 0, 0), X(−0.5, −0.5, 0), P(0.75, −0.25, −0.25), and Z(0.5, 0.5, −0.5). The (001) surface BZ shows in labeling with , , and . Paths labeled in green display the k-path selection for the comparison of bulk and surface states calculations.
3.2. Volume Optimization
Since the volume that shows the lowest total energy can be identified as the ground state for the stable structure, we first optimize the crystals to find the cell volume corresponding to the lowest total energy. In our calculations, we performed the geometry optimizations of the unit cell by allowing atomic positions to be rearranged and the lattice parameters to move around together. We followed the Quantum Espresso volume optimization scheme with extreme convergence for non-relativistic ultra-soft pseudo-potentials. The optimized lattice constants a and c for BZn are shown in the second and third columns of Table 1. Similarly calculated lattice positions for the optimized system are Zn(0, 0, 0), B1(0.25, 0.75, 0.50), B2(0.75, 0.25, 0.50), with a little differentiation of the Ir, Rh, and Co positions as Ir1(x, x, 0), Ir2(1 − x, 1 − x, 0), Rh1(y, y, 0), Rh2(1 − y, 1 − y, 0), Co1(z, z, 0), and Co2(1 − z, 1 − z, 0) with x = 0.3725808923, y = 0.3715044822, and z = 0.3712045162. Hence, the crystal structures at optimized bulk lattice parameters and atomic positions are used for further investigation of BZn properties during the project.

Table 1.
The calculated lattice constants a, c, and formation energies, E, of BZn compounds.
3.3. Formation Energy
Since the compounds that show negative formation energies at thermal equilibrium with respect to their elemental phases are known to be stable, we calculate the formation energy to study the stability of the structures. In general, the formation energy per atom for ternary BZn can be calculated as
where , , and are the numbers of B, X (Ir, Rh, Co), and Zn atoms in the unit cell, respectively. Since the BZn unit cell has 1 atom of Zn and 2 atoms of B and X, and are taken. is the calculated total free energy of the compound, and , , and are the calculated total free energies per atom of the elemental phases of B, X, and Zn, respectively.
During the total energy calculation of B, X, and Zn, we use optimized structures of trigonal crystal of space group 166 (Rm) for B, a cubic crystal of space group 225 (Fmm) for X, and hexagonal crystal of space group 194 (/mmc) for Zn. By using Equation (1) we calculate the formation energy for BZn as −0.3005 eV/atom, −0.3245 eV/atom, and −0.2279 eV/atom, for X = Ir, Rh, and Co respectively, the last column of Table 1. Since all three compounds indicate negative formation energies with respect to their elemental phases, we identify these structures are theoretically stable.
3.4. Elastic Properties
The first-principles density functional calculation implemented on QE was used to explore the mechanical properties of the structures. Mechanical properties together with crystal stability and stiffness are easily investigated by calculating the elastic stiffness matrix or flexibility matrix, (. The bulk modulus, Young’s modulus, shear modulus, and Poisson’s ratio of polycrystals are calculated by using Voigt–Reuss approximation methods [73]. Average poly-crystalline modules (Hill’s average) are obtained by using the upper and lower limit of the actual effective modulus corresponding to the Voigt bound and Reuss bound. The Hill’s average is said to be mostly agreed with the experimental result [73]. Since the structure is a tetragonal crystal, there are six independent non-zero elastic constants, namely and . The calculated elastic constants and effective bulk, shear, and Young’s modules for BZn are presented in Table 2.

Table 2.
The calculated elastic constants (), bulk modulus (B), shear modulus (G), Young’s modulus (E) in units of GPa, and Poisson’s ratio () for the BZn compounds.
The elastic constants calculated for the tetragonal crystal satisfy the following Born mechanical stability criteria as discussed in the Refs. [74,75]:
where represent six independent non-zero elastic constants. The elastic tensor of the second order is calculated by using the expansion of the elastic energy in terms of the applied strain. The results are obtained for large deformations with high-order polynomial fit by identifying the plateau regions which provide good, reasonable results [73]. Calculated elastic constants for all three BZn compounds satisfy the Born mechanical stability criteria implemented in Equation (2).
3.5. Phonon Frequencies
A collective excitation of a set of atoms that decomposes into different modes plays an essential role in material science. Therefore, we performed the first principles of phonon calculations with force constants which are said to be an important calculation for studying dynamical behaviors and thermal properties of the materials. Studying topological phonons and their properties is another frontier research field that we are not discussing here. Our focus here is to check the dynamical stability of the samples by observing non-imaginary phonon frequencies. The vibrational band structures of BZn do not have regions with imaginary frequencies as shown in Figure 2 which implies phonon stability of the samples. It should be noted that the phonon calculation is the most widely used in the stability analysis, therefore those compounds are likely to be realized experimentally.
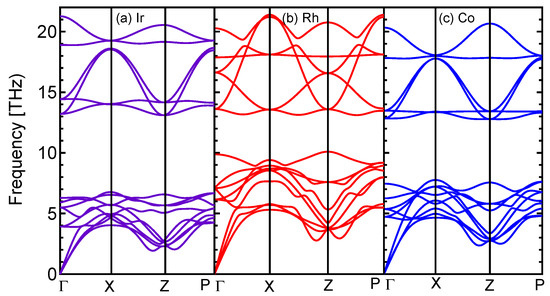
Figure 2.
(Color online) Calculated phonon spectra of BZn (X = Ir, Rh, Co) compounds. All three phonon spectra were calculated without the SOC effect and are shown on the k-path -X-Z-P. (a) The phonon spectrum of the Ir sample, (b) the same for the Rh sample, and (c) the same for the Co sample.
Due to the negative formation energies with the fulfillment of the mechanical stability scheme and non-imaginary phonon spectra of all three BZn compounds, we conclude that all three compounds are mechanically, structurally, and dynamically stable.
3.6. Electronic Band Structure and DOS Properties
An electronic band structure calculation of BIrZn with GGA with and without the inclusion of the SOC along the high-symmetry k-path -X-Z-P- was plotted by setting the Fermi level at 0 eV on the energy scale as shown in Figure 3. The top panel, (a), shows the band structure of the BIrZn compound with the inclusion of the SOC effect, and the bottom panel, (c), shows the calculated electronic band structure without the inclusion of the SOC effect in irreducible representation. Irreducible representation (symmorphic crystal symmetries) of the band structure shows band symmetries by using different colored solid lines. There were a few bands near the Fermi level. Interesting band features near the Fermi level were noted around X and P points. Since irreducible representation allows us to access each eigenvalue along the chosen k-path, we can identify connecting lines of bands and the symmetries by looking for the same colored bands for the same symmetry [76,77].
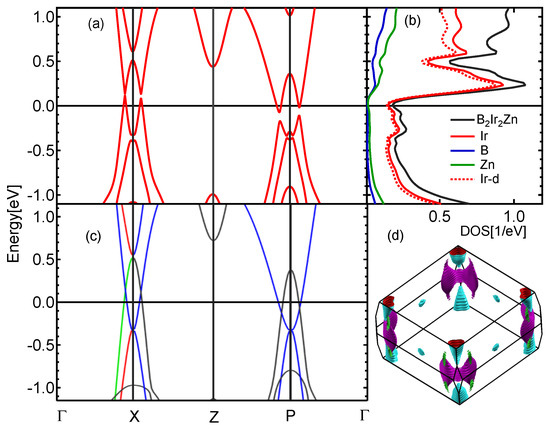
Figure 3.
(Color online) Calculated electronic band structure of BIrZn compound with and without SOC interaction along the high symmetry lines on the BZ k-path -M-X-Z-P-. (a) Calculated bulk band structure with SOC effect. (b) Calculated atom-projected DOS for BIrZn with SOC and total DOS with SOC effect. (c) An irreducible representation of the calculated bulk band structure without SOC. Colors have the meaning of band symmetries discussed in the text. The solid black line at zero in (a–c) indicates the Fermi level. (d) The Fermi surface of BIrZn bands.
The two linear upright crossings in the -X-Z plane are identified as Dirac-like crossings. Since the SOC (some of the degenerate atomic levels split without magnetic field) have appeared as promising candidates for exotic band behaviors of Dirac materials, we performed SOC calculation to identify the topological features at the crossings. As shown in Figure 3a, it is clear that those crossings are gapped out with the inclusion of SOC. The Dirac point located at (0.136 eV) with the coordination of was gapped out into two-fold degeneracy. The blue color represents the and green color represents the in irreducible representations with space group . The Dirac point located at (0.110 eV) is gapped out into two-fold degeneracy. Blue color represents the and black color represents the in irreducible representations with space group . Therefore, both crossings are identified as type I Dirac points. The lines at crossing points display the same and opposite slopes around ±7 eV Å. These Dirac points are protected by the absence of SOC with the predicted electron velocity of around Å/s calculated by , which is similar to the experimentally measured velocity of CdAs [14].
The two crossings located at the Z-P- plane (left at −0.128 eV and right at −0.061 eV) are gapped out again into two-fold degeneracy with band inversion. At the left crossing, black and blue bands represent the and in an orderly space group . At the right crossing, black and blue colors represent the and , respectively with space group . Therefore, both crossings at around −0.128 eV and −0.061 eV are identified as type I Dirac points. The lines at crossing points display the same and opposite slopes around ±5 eV Å. These Dirac points are protected by the absence of SOC but gap out by the presence of SOC. It is also observed that there is a band inversion during the gap-out. All the band crossings near Fermi energy are identified mainly as Ir-d orbitals barely hybridized with all p orbitals by using the fat band orientations.
The results of total and partial DOS of BIrZn provide valuable information about the origin of bands with contributions from each atom and each orbital. Total and atom-projected DOS calculations without the SOC effect for the BIrZn display in Figure 3c. Black solid lines represent the total DOS from all atoms of the BIrZn compound. Red, blue, and green represent the atom-projected total DOS for Ir, B, and Zn atoms, respectively. The total DOS at the Fermi level is around 0.25 states per eV per unit cell and is dominated by the Ir atom DOS. Further, the total DOS at the Fermi level is dominated by Ir-d orbitals denoted by red dotted lines. This agrees with the fat band orientations we discussed in the bands’ diagram in Figure 3.
The calculated Fermi surfaces are displayed in Figure 3d by indicating cone-shaped Fermi pockets at the corner of the Fermi surface within the BZ.
This work is extended to the classification of band structures in a different direction including crystal point group symmetries. Recent studies of topological materials reveal a large class of materials with gapless surface states. Among them, topological insulating states protected by crystal symmetries, rather than time-reversal symmetry, have been introduced as topological crystalline insulators. This motivated us to investigate topological crystalline insulators’ behaviors of the compound. Since the structure is tetragonal as in Figure 1, there is no direct projection of the bulk Brillouin zone to the surface Brillouin zone to observe the surface states in Z-P-. However, we decided to look for the other possible surface Brillouin zones, as in Figure 1c. The projection of N-X- in bulk BZ represents the -- in (001) surface BZ. In Figure 1a, represents the (001) surface BZ. Calculated surface states on the k-path labeled in green are displayed on the right, top-to-bottom by using red solid lines for different termination layers as in (b-i), (c-i), and (d-i) of Figure 4. To study the surface states compared to bulk bands, we plotted the bulk band on top of the surface bands by using blue solid lines. All the calculations were performed for relativistic potentials. We found that all B, Ir, and Zn termination layers show the same features of surface states although they show different band densities. Additionally, we investigated clear surface states on the X-N plane since there is no crossing observed in bulk bands. The surface states on the X- plane were barely recognized due to small gap openings of bulk bands. As is evident, we were unable to project the interested exact bulk Brillouin band k-path in Figure 3 to any surface Brillouin zone path directly. That was the reason to look at the (001) surface plane with the projection of N-X- to see surface states near the Fermi level.
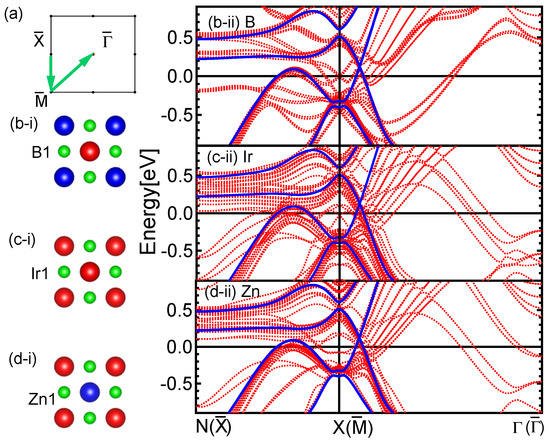
Figure 4.
(Color online) Calculated surface states of (001) plane. (a) The (001) surface BZ shown in labeling with , , and . Paths labeled in green display the k-path selection. (b-i) Shows the arrangement of atoms for the B1 layer and (b-ii) shows the surface states of the B-termination layer with 25 layers of atoms. (c-i) Shows the arrangement of atoms for the Ir1 layer and (c-ii) shows the surface states of the Ir-termination layer with 21 layers of atoms. Similarly, (d-i) shows the arrangement of atoms for the Zn1 layer, and (d-ii) shows the surface states of the B-termination layer with 23 layers of atoms. The arrangement of atoms for each layer (Zn1, X1, and B1) is noted in Figure 1. Surface bands are denoted by red solid lines and bulk bands are shown in blue solid lines as a comparison. All surface and bulk band calculations were performed including the SOC effect. The solid black horizontal line at zero indicates the Fermi level.
We further studied the BIrZn by investigating the dependence of the band gap on the lattice constants since it can be used as another signature of topological crystalline materials as discussed in the Ref. [43]. We investigated the band gap as a function of the percentage of lattice parameters. The behavior of the two crossings identified as Dirac points on the -X-Z plane in Figure 3 was investigated as shown in the top panel of Figure 5. It displays that there is no manifest effect to change of lattice parameters even by compressing or stretching. We were barely able to identify the gap closing of the X- plane around 5% of lattice compressing, but no effect was identified on the X-Z plane. The behavior of the two crossings identified as Dirac points with band inversion Z-P- path in Figure 3 was investigated as shown in the bottom left panel of Figure 5. It displays that there is a considerable effect on band gap with respect to lattice parameters by stretching. As the lattice parameters increase, the band gap of BIrZn decreases to zero and then re-opens. This gap closing signals a topological crystalline insulator at that ambient pressure which is expected to close 13% of stretching of the lattice. The energy gap as a function of the percentage change of lattice parameters is displayed in Figure 5i by denoting a purple solid color for Z-P and brown solid color for P- paths. Continuously tunable band gaps may lead to wide-ranging applications in thermoelectrics, infrared detection, and tunable electronics.
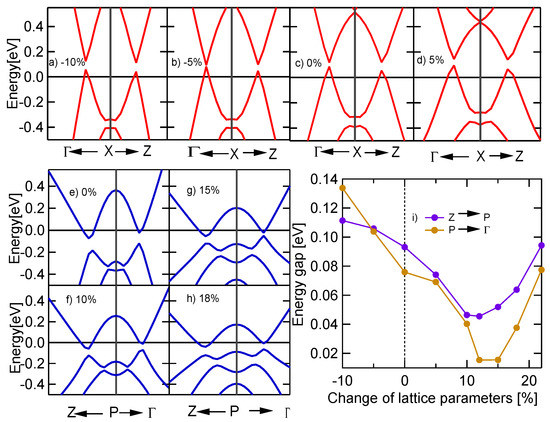
Figure 5.
(Color online) The change in band energy gap around the Fermi level of the BIrZn sample with SOC effect by changing the volume of the lattice. Top panel (a–d): shows the effect of gap changes due to the compression and stretch of the lattice for two crossings in X- and X-Z paths for −10%, −5%, 0%, and 5% shown from left to right, respectively. Bottom panel (e–i): The plots on the left show two crossings in the Z-P- k-path with their related stretch percentages in volume. The graph on the right compares both crossings’ energy gap to the percentage of lattice parameters in P-Z and P- paths on the left. The dotted back vertical line at 0% represents the optimized lattice. The solid black horizontal line at zero indicates the Fermi level in all plots.
We performed the electronic band structure and DOS calculations for BRhZn and BCoZn by using the same structure as BIrZn. All the calculations were performed by using the optimized lattice parameters from Table 1 and including the SOC effect as shown in (a) and (b) of Figure 6. We conclude that all three compounds display the same band characteristics as discussed above for BIrZn. The energy locations of four crossing points are a little different than the BIrZn. It is also identified that the band structure is more compressed toward the Fermi energy in Co and Rh than Ir. The DOS features around the Fermi level are investigated in three samples with and without the SOC effect, as shown in (c) of Figure 6. We did not identify the manifest SOC effect in DOS by comparing solid and dotted color lines represented with and without relativistic potentials. Figure 6 shows that Co has more DOS near Fermi energy than Rh, and Rh has more DOS than Ir.
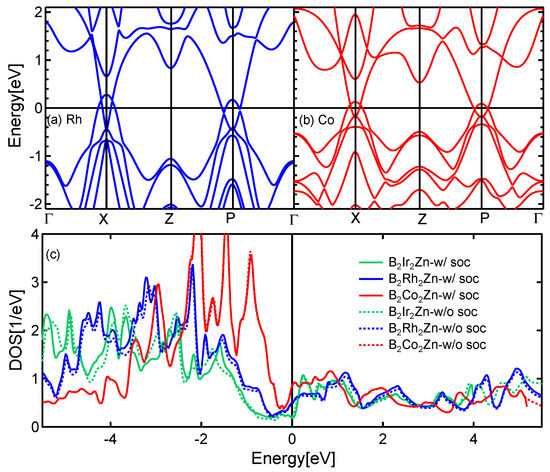
Figure 6.
(Color online) Calculated band structure of BZn (X = Rh, Co) without SOC, and DOS of BZn (X = Ir, Rh, Co) with and without the SOC effect. (a,b) Display of the band structure of Rh and Co samples respectively. (c) Shows total DOS for all three samples with solid and dotted lines representing calculations with and without the SOC effect, respectively. The solid black line at zero indicates the Fermi level in all plots.
4. Conclusions
In summary, newly designed BZn (X = Ir, Rh, Co) compounds show interesting topological properties and the hallmark of the topological features. Dirac band behaviors near the Fermi level with the effect of spin–orbit coupling can be used to predict theoretical and experimental significance on material properties. Linear band crossings near the Fermi level are discovered. Type I Dirac crossings were identified by investigating the SOC effect. We performed the surface states calculation on high symmetric crystal surfaces by projecting to the (001) plane to look for topological crystalline insulating properties, although there is no direct projection from the bulk path to the surface Brillouin zone. Therefore, we looked for the gapping behavior quantitatively to signify that this compound has TCI features. The gap was investigated by applying stress and strain to the lattice volume. It showed that the gap is closing by stretching the lattice and also re-opening for further stretching which can be used to identify the sample as the topological crystalline insulator. Further, we calculated elastic constants, formation energy, and phonon spectra to predict the mechanical, structural, and dynamical stabilities of the compounds. The predicted electronic structures of BZn compounds, their important topological properties, and stability criteria will be useful for investigating the sample for further studies. Since these materials show high mobilities and a wide range of functionalities, it creates an extremely valuable platform for exploring advanced technology.
Author Contributions
K.H. and N.H. wrote the manuscript with the contribution of J.H. and A.R. J.H. contributes to data analysis and simulation. J.H. and A.R. validate the results and contribute to data analysis and discussion. K.H. and N.H. conceptualize, supervise, validate, visualize, and review the results. All authors have read and agreed to the published version of the manuscript.
Funding
N.H. and K.H. acknowledge the Extreme Science and Engineering Discovery Environment (XSEDE), supported by grant number TG-PHY190050. K.H. and J.H. acknowledge the financial support from Undergraduate Prestigious Fellowships from Seton Hall University.
Conflicts of Interest
We all certify that we have no affiliations with or involvement in any organization or entity with any financial interest or non-financial interest in the subject matter or materials discussed in this paper. The authors declare no conflict of interest.
References
- Kane, C.L.; Mele, E.J. Z2 topological order and the quantum spin hall effect. Phys. Rev. Lett. 2005, 95, 146802. [Google Scholar] [CrossRef]
- Kane, C.L.; Mele, E.J. Quantum spin hall effect in graphene. Phys. Rev. Lett. 2005, 95, 226801. [Google Scholar] [CrossRef]
- Hasan, M.Z.; Kane, C.L. Topological insulators. Rev. Mod. Phys. 2010, 82, 3045. [Google Scholar] [CrossRef]
- Qi, X.L.; Zhang, S.C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057. [Google Scholar] [CrossRef]
- Yang, B.J.; Nagaosa, N. Classification of stable three-dimensional Dirac semimetals with nontrivial topology. Nat. Commun. 2014, 5, 4898. [Google Scholar] [CrossRef]
- Xu, G.; Weng, H.; Wang, Z.; Dai, X.; Fang, Z. Chern Semimetal and the Quantized Anomalous Hall Effect in HgCr2Se4. Phys. Rev. Lett. 2011, 107, 186806. [Google Scholar] [CrossRef] [PubMed]
- Zyuzin, A.A.; Wu, S.; Burkov, A.A. Weyl semimetal with broken time reversal and inversion symmetries. Phys. Rev. B 2012, 85, 165110. [Google Scholar] [CrossRef]
- Liu, Z.K.; Zhou, B.; Zhang, Y.; Wang, Z.J.; Weng, H.M.; Prabhakaran, D.; Mo, S.K.; Shen, Z.X.; Fang, Z.; Dai, X.; et al. Discovery of a Three-Dimensional Topological Dirac Semimetal, Na3Bi. Science 2014, 343, 864–867. [Google Scholar] [CrossRef]
- Neupane, M.; Xu, S.Y.; Sankar, R.; Alidoust, N.; Bian, G.; Liu, C.; Belopolski, I.; Chang, T.R.; Jeng, H.T.; Lin, H.; et al. Observation of a three-dimensional topological Dirac semimetal phase in high-mobility Cd3As2. Nat. Commun. 2014, 5, 3786. [Google Scholar] [CrossRef]
- Yan, M.; Huang, H.; Zhang, K.; Wang, E.; Yao, W.; Deng, K.; Wan, G.; Zhang, H.; Arita, M.; Yang, H.; et al. Lorentz-violating type-II Dirac fermions in transition metal dichalcogenide PtTe2. Nat. Commun. 2017, 8, 257. [Google Scholar] [CrossRef]
- Noh, H.J.; Jeong, J.; Cho, E.J.; Kim, K.; Min, B.I.; Park, B.G. Experimental Realization of Type-II Dirac Fermions in a PdTe2 Superconductor. Phys. Rev. Lett. 2017, 119, 016401. [Google Scholar] [CrossRef] [PubMed]
- Gibson, Q.D.; Schoop, L.M.; Muechler, L.; Xie, L.S.; Hirschberger, M.; Ong, N.P.; Car, R.; Cava, R.J. Three-dimensional Dirac semimetals: Design principles and predictions of new materials. Phys. Rev. B 2015, 91, 205128. [Google Scholar] [CrossRef]
- Schoop, L.M.; Pielnhofer, F.; Lotsch, B.V. Chemical principles of topological semimetals. Chem. Mater. 2018, 30, 3155–3176. [Google Scholar] [CrossRef]
- Liang, T.; Gibson, Q.; Ali, M.N.; Liu, M.; Cava, R.J.; Ong, N.P. Ultrahigh mobility and giant magnetoresistance in the Dirac semimetal Cd3As2. Nat. Mater. 2015, 14, 280–284. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.Y.; Belopolski, I.; Alidoust, N.; Neupane, M.; Bian, G.; Zhang, C.; Sankar, R.; Chang, G.; Yuan, Z.; Lee, C.C.; et al. Discovery of a Weyl fermion semimetal and topological Fermi arcs. Science 2015, 349, 613–617. [Google Scholar] [CrossRef] [PubMed]
- Lv, B.Q.; Xu, N.; Weng, H.M.; Ma, J.Z.; Richard, P.; Huang, X.C.; Zhao, L.X.; Chen, G.F.; Matt, C.E.; Bisti, F.; et al. Observation of Weyl nodes in TaAs. Nat. Phys. 2015, 11, 724–727. [Google Scholar] [CrossRef]
- Soluyanov, A.A.; Gresch, D.; Wang, Z.; Wu, Q.; Troyer, M.; Dai, X.; Bernevig, B.A. Type-II Weyl semimetals. Nature 2015, 527, 495–498. [Google Scholar] [CrossRef]
- Huang, S.M.; Xu, S.Y.; Belopolski, I.; Lee, C.C.; Chang, G.; Wang, B.; Alidoust, N.; Bian, G.; Neupane, M.; Zhang, C.; et al. A Weyl Fermion semimetal with surface Fermi arcs in the transition metal monopnictide TaAs class. Nat. Commun. 2015, 6, 7373. [Google Scholar] [CrossRef]
- Deng, K.; Wan, G.; Deng, P.; Zhang, K.; Ding, S.; Wang, E.; Yan, M.; Huang, H.; Zhang, H.; Xu, Z.; et al. Experimental observation of topological Fermi arcs in type-II Weyl semimetal MoTe2. Nat. Phys. 2016, 12, 1105–1110. [Google Scholar] [CrossRef]
- Xu, N.; Weng, H.M.; Lv, B.Q.; Matt, C.E.; Park, J.; Bisti, F.; Strocov, V.N.; Gawryluk, D.; Pomjakushina, E.; Conder, K.; et al. Observation of Weyl nodes and Fermi arcs in tantalum phosphide. Nat Commun. 2016, 7, 11006. [Google Scholar] [CrossRef]
- Yu, R.; Weng, H.; Fang, Z.; Dai, X.; Hu, X. Topological Node-Line Semimetal and Dirac Semimetal State in Antiperovskite Cu3PdN. Phys. Rev. Lett. 2015, 115, 036807. [Google Scholar] [CrossRef]
- Xie, L.S.; Schoop, L.M.; Seibel, E.M.; Gibson, Q.D.; Xie, W.; Cava, R.J. A New Form Ca3P2 A Ring Dirac Nodes. APL Mater. 2015, 3, 083602. [Google Scholar] [CrossRef]
- Xu, Q.; Yu, R.; Fang, Z.; Dai, X.; Weng, H. Topological nodal line semimetals in the CaP3 family of materials. Phys. Rev. B 2017, 95, 045136. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, G. A New Strongly Topological Node-Line Semimetals β-PbO2. Phys. Lett. A 2017, 381, 2856–2859. [Google Scholar] [CrossRef]
- Yamakage, A.; Yamakawa, Y.; Tanaka, Y.; Okamoto, Y. Line-node Dirac semimetal and topological insulating phase in noncentrosymmetric pnictides CaAgX (X = P, As). J. Phys. Soc. Jpn. 2016, 85, 013708. [Google Scholar] [CrossRef]
- Feng, X.; Yue, C.; Song, Z.; Wu, Q.; Wen, B. Topological Dirac nodal-net fermions in AlB2-Type TiB2 ZrB2. Phys. Rev. Mater. 2018, 2, 014202. [Google Scholar] [CrossRef]
- Huang, H.; Liu, J.; Vanderbilt, D.; Duan, W. Topological nodal-line semimetals in alkaline-earth stannides, germanides, and silicides. Phys. Rev. B 2016, 93, 201114. [Google Scholar] [CrossRef]
- Hirayama, M.; Okugawa, R.; Miyake, T.; Murakami, S. Topological Dirac nodal lines and surface charges in fcc alkaline earth metals. Nat. Commun. 2017, 8, 14022. [Google Scholar] [CrossRef]
- Mikitik, G.P.; Sharlai, Y.V. Band-contact lines in the electron energy spectrum of graphite. Phys. Rev. B 2006, 73, 235112. [Google Scholar] [CrossRef]
- Lou, R.; Ma, J.Z.; Xu, Q.N.; Fu, B.B.; Kong, L.Y.; Shi, Y.G.; Richard, P.; Weng, H.M.; Fang, Z.; Sun, S.S.; et al. Emergence of topological bands on the surface of ZrSnTe crystal. Phys. Rev. B 2016, 93, 241104. [Google Scholar] [CrossRef]
- Takane, D.; Wang, Z.; Souma, S.; Nakayama, K.; Trang, C.X.; Sato, T.; Takahashi, T.; Ando, Y. Dirac-node arc in the topological line-node semimetal HfSiS. Phys. Rev. B 2016, 94, 121108. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, L.L.; Mun, E.; Johnson, D.D.; Mou, D.; Huang, L.; Lee, Y.; Bud’ko, S.L.; Canfield, P.C.; Kaminski, A. Dirac node arcs in PtSn4. Nat. Phys. 2016, 12, 667–671. [Google Scholar] [CrossRef]
- Bian, G.; Chang, T.R.; Sankar, R.; Xu, S.Y.; Zheng, H.; Neupert, T.; Chiu, C.K.; Huang, S.M.; Chang, G.; Belopolski, I.; et al. Topological nodal-line fermions in spin–orbit metal PbTaSe2. Nat. Commun. 2016, 7, 10556. [Google Scholar] [CrossRef] [PubMed]
- Topp, A.; Lippmann, J.M.; Varykhalov, A.; Duppel, V.; Lotsch, B.V.; Ast, C.R.; Schoop, L.M. Non-Symmorphic Band Degeneracy Fermi Level ZrSiTe. New J. Phys. 2016, 18, 125014. [Google Scholar] [CrossRef]
- Haubold, E.; Koepernik, K.; Efremov, D.; Khim, S.; Fedorov, A.; Kushnirenko, Y.; Van Den Brink, J.; Wurmehl, S.; Büchner, B.; Kim, T.K.; et al. Experimental realization of type-II Weyl state in noncentrosymmetric TaIrTe4. Phys. Rev. B 2017, 95, 241108. [Google Scholar] [CrossRef]
- Schoop, L.M.; Ali, M.N.; Straßer, C.; Topp, A.; Varykhalov, A.; Marchenko, D.; Duppel, V.; Parkin, S.S.; Lotsch, B.V.; Ast, C.R. Dirac cone protected by non-symmorphic symmetry and three-dimensional Dirac line node in ZrSiS. Nat. Commun. 2016, 7, 11696. [Google Scholar] [CrossRef]
- Hu, J.; Tang, Z.; Liu, J.; Liu, X.; Zhu, Y.; Graf, D.; Myhro, K.; Tran, S.; Lau, C.N.; Wei, J.; et al. Evidence of topological nodal-line fermions in ZrSiSe and ZrSiTe. Phys. Rev. Lett. 2016, 117, 016602. [Google Scholar] [CrossRef]
- Mong, R.S.; Essin, A.M.; Moore, J.E. Antiferromagnetic topological insulators. Phys. Rev. B 2010, 81, 245209. [Google Scholar] [CrossRef]
- Teo, J.C.; Fu, L.; Kane, C.L. Surface states and topological invariants in three-dimensional topological insulators. Phys. Rev. B 2008, 78, 045426. [Google Scholar] [CrossRef]
- Xia, Y.; Qian, D.; Hsieh, D.; Wray, L.; Pal, A.; Lin, H.; Bansil, A.; Grauer, D.H.Y.S.; Hor, Y.S.; Cava, R.J.; et al. Observation of a large-gap topological-insulator class with a single Dirac cone on the surface. Nat. Phys. 2009, 5, 398. [Google Scholar] [CrossRef]
- Chen, Y.L.; Analytis, J.G.; Chu, J.H.; Liu, Z.K.; Mo, S.K.; Qi, X.L.; Zhang, H.J.; Lu, D.H.; Dai, X.; Fang, Z.; et al. Experimental Realization of a Three-Dimensional Topological Insulator, Bi2Te3. Science 2009, 325, 178–181. [Google Scholar] [CrossRef] [PubMed]
- Hsieh, D.; Xia, Y.; Qian, D.; Wray, L.; Meier, F.; Dil, J.H.; Osterwalder, J.; Patthey, L.; Fedorov, A.V.; Lin, H.; et al. Observation of Time-Reversal-Protected Single-Dirac-Cone Topological-Insulator States in Bi2Te3 and Sb2Te3. Phys. Rev. Lett. 2009, 103, 146401. [Google Scholar] [CrossRef] [PubMed]
- Hsieh, T.H.; Lin, H.; Liu, J.; Duan, W.; Bansil, A.; Fu, L. Topological crystalline insulators in the SnTe material class. Nat. Commun. 2012, 3, 982. [Google Scholar] [CrossRef] [PubMed]
- Slager, R.J.; Mesaros, A.; Juričić, V.; Zaanen, J. The space group classification of topological band-insulators. Nat. Phys. 2013, 9, 98–102. [Google Scholar] [CrossRef]
- Kruthoff, J.; De Boer, J.; Van Wezel, J.; Kane, C.L.; Slager, R.J. Topological classification of crystalline insulators through band structure combinatorics. Phys. Rev. X 2017, 7, 041069. [Google Scholar] [CrossRef]
- Fu, L. Topological crystalline insulators. Phys. Rev. Lett. 2011, 106, 106802. [Google Scholar] [CrossRef]
- Fang, C.; Fu, L. New classes of topological crystalline insulators having surface rotation anomaly. Sci. Adv. 2019, 5, eaat2374. [Google Scholar] [CrossRef]
- Weng, H.; Zhao, J.; Wang, Z.; Fang, Z.; Dai, X. Topological crystalline kondo insulator in mixed valence ytterbium borides. Phys. Rev. Lett. 2014, 112, 016403. [Google Scholar] [CrossRef]
- Hsieh, T.H.; Liu, J.; Fu, L. Topological crystalline insulators and Dirac octets in antiperovskites. Phys. Rev. B 2014, 90, 081112. [Google Scholar] [CrossRef]
- Tanaka, Y.; Ren, Z.; Sato, T.; Nakayama, K.; Souma, S.; Takahashi, T.; Segawa, K.; Ando, Y. Experimental realization of a topological crystalline insulator in SnTe. Nat. Phys. 2012, 8, 800–803. [Google Scholar] [CrossRef]
- Dziawa, P.; Kowalski, B.J.; Dybko, K.; Buczko, R.; Szczerbakow, A.; Szot, M.; Łusakowska, E.; Balasubramanian, T.; Wojek, B.M.; Berntsen, M.H.; et al. Topological crystalline insulator states in Pb1-xSnxSe. Nat. Mat. 2012, 11, 1023. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.Y.; Liu, C.; Alidoust, N.; Neupane, M.; Qian, D.; Belopolski, I.; Denlinger, J.D.; Wang, Y.J.; Lin, H.; Wray, L.A.; et al. Observation of a topological crystalline insulator phase and topological phase transition in Pb1-xSnxTe. Nat. Commun. 2012, 3, 1192. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Hsu, C.H.; Chang, T.R.; Tien, H.J.; Ma, Q.; Jarillo-Herrero, P.; Gedik, N.; Bansil, A.; Pereira, V.M.; Xu, S.Y.; et al. Topological crystalline insulator states in the Ca2As family. Phys. Rev. B 2018, 98, 241104. [Google Scholar] [CrossRef]
- Barone, P.; Rauch, T.; Di Sante, D.; Henk, J.; Mertig, I.; Picozzi, S. Pressure-induced topological phase transitions in rocksalt chalcogenides. Phys. Rev. B 2013, 88, 045207. [Google Scholar] [CrossRef]
- Munoz, F.; Vergniory, M.G.; Rauch, T.; Henk, J.; Chulkov, E.V.; Mertig, I.; Botti, S.; Marques, M.A.; Romero, A.H. Topological crystalline insulator in a new Bi semiconducting phase. Sci. Rep. 2016, 6, 21790. [Google Scholar] [CrossRef]
- Howard, J.; Steier, J.; Haldolaarachchige, N.; Hettiarachchilage, K. Computational Prediction of New Series of Topological Ternary Compounds LaXS (X = Si, Ge, Sn) First-Principles. J 2021, 4, 577–588. [Google Scholar] [CrossRef]
- Zhang, X.; Jin, L.; Dai, X.; Liu, G. Topological type-II nodal line semimetal and Dirac semimetal state in stable kagome compound Mg3Bi2. J. Phys. Chem. Lett. 2017, 8, 4814–4819. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, Y.; Chen, X.Q.; Franchini, C.; Xu, G.; Weng, H.; Dai, X.; Fang, Z. Dirac semimetal and topological phase transitions in A3Bi (A = Na, K, Rb). Phys. Rev. B 2012, 85, 195320. [Google Scholar] [CrossRef]
- Schoop, L.M.; Topp, A. Topological Materials and Solid-State Chemistry-Finding and Characterizing New Topological Materials. Topol. Matter. Springer Ser. Solid-State Sci. 2018, 190, 211–243. [Google Scholar]
- Sun, Y.; Felser., C. Topological Materials in Heusler Compounds. Topol. Matter Springer Ser. Solid-State Sci. 2018, 190, 199–210. [Google Scholar]
- Narang, P.; Garcia, C.A.; Felser, C. The topology of electronic band structures. Nat. Mater. 2021, 20, 293–300. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter. 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Nardelli, M.B.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter. 2017, 29, 465901. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Singh, D.J.; Nordstrom, L. Planewaves, Pseudopotentials, and the LAPW Method, 2nd ed.; Springer: New York, NY, USA, 2006; pp. 1–134. [Google Scholar]
- Sjöstedt, E.; Nordström, L.; Singh, D.J. An alternative way of linearizing the augmented plane-wave method. Solid State Commun. 2000, 114, 15–20. [Google Scholar] [CrossRef]
- Madsen, G.K.; Blaha, P.; Schwarz, K.; Sjöstedt, E.; Nordström, L. Efficient linearization of the augmented plane-wave method. Phys. Rev. B 2001, 64, 195134. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Blaha, P.; Schwarz, K.; Sorantin, P.; Trickey, S.B. Full-potential, linearized augmented plane wave programs for crystalline systems. Commput. Phys. Commun. 1990, 59, 399–415. [Google Scholar] [CrossRef]
- Blaha, P.; Schwarz, K.; Tran, F.; Laskowski, R.; Madsen, G.K.; Marks, L.D. WIEN2k: An APW+ lo program for calculating the properties of solids. J. Chem. Phys. 2020, 152, 074101. [Google Scholar] [CrossRef]
- Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef]
- Golesorkhtabar, R.; Pavone, P.; Spitaler, J.; Puschnig, P.; Draxl, C. ElaStic: A tool for calculating second-order elastic constants from first principles. Comput. Phys. Commun. 2013, 184, 1861–1873. [Google Scholar] [CrossRef]
- Born, M. On the stability of crystal lattices. I Math. Proc. Camb. Philos. Soc. 1940, 36, 160–172. [Google Scholar] [CrossRef]
- Mouhat, F.; Coudert, F.X. Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B 2014, 90, 224104. [Google Scholar] [CrossRef]
- Kittle, C. Introduction to Solid State Physics, 8th ed.; John Wiley & Sons: New York, NY, USA, 2004; pp. 1–704. [Google Scholar]
- Koster, G.F.; Dimmock, J.D.; Wheeler, R.G.; Statz, H. Properties of the Thirty-Two Point Groups, 1st ed.; MIT Press: Cambridge, MA, USA, 1963; pp. 1–104. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).