Influence of Wooden Compartment’s Fuel Moisture Content on Time to Flashover: An Experimental and Numerical Study
Abstract
:1. Introduction
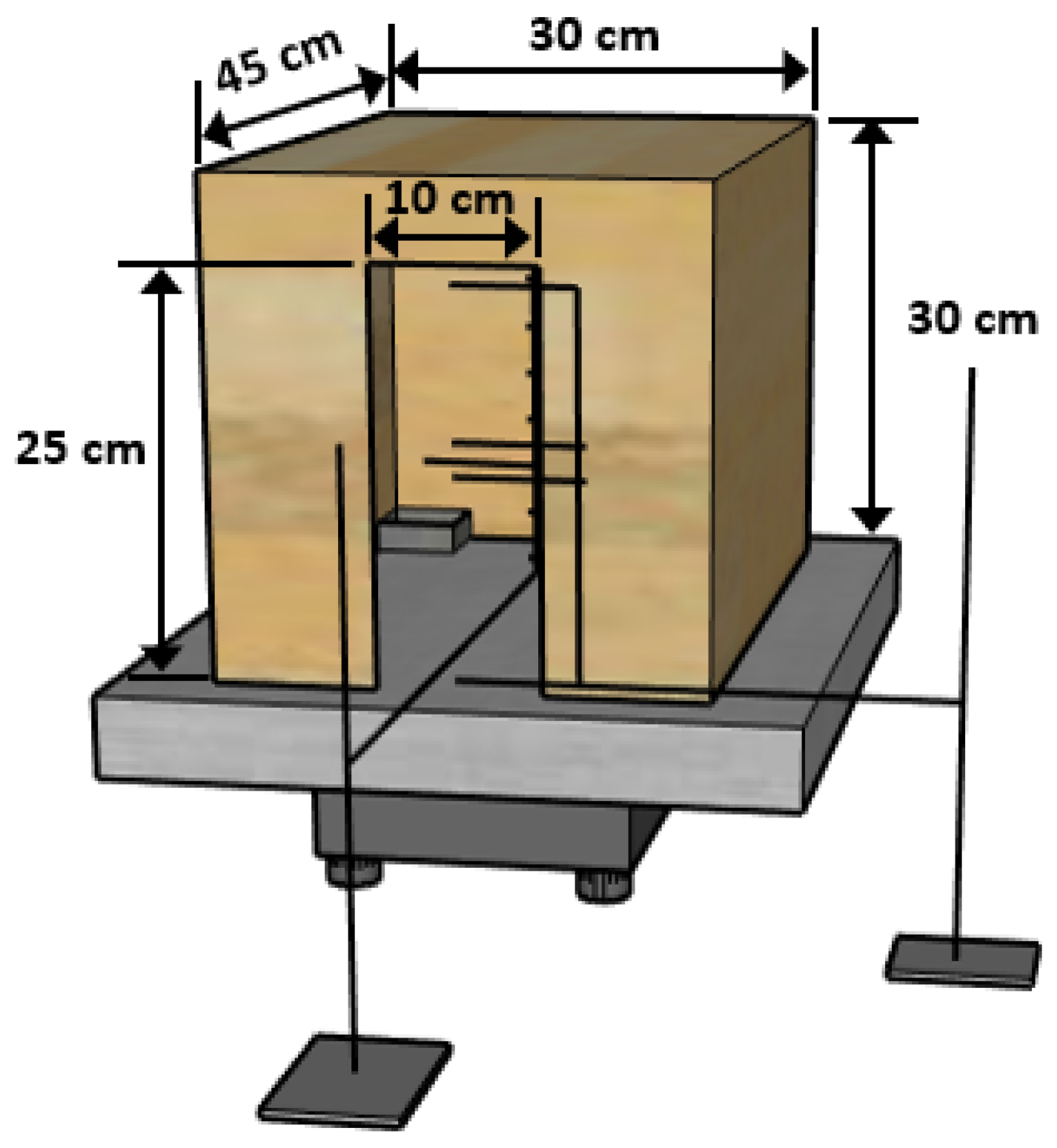
2. Experimental Design and Procedure
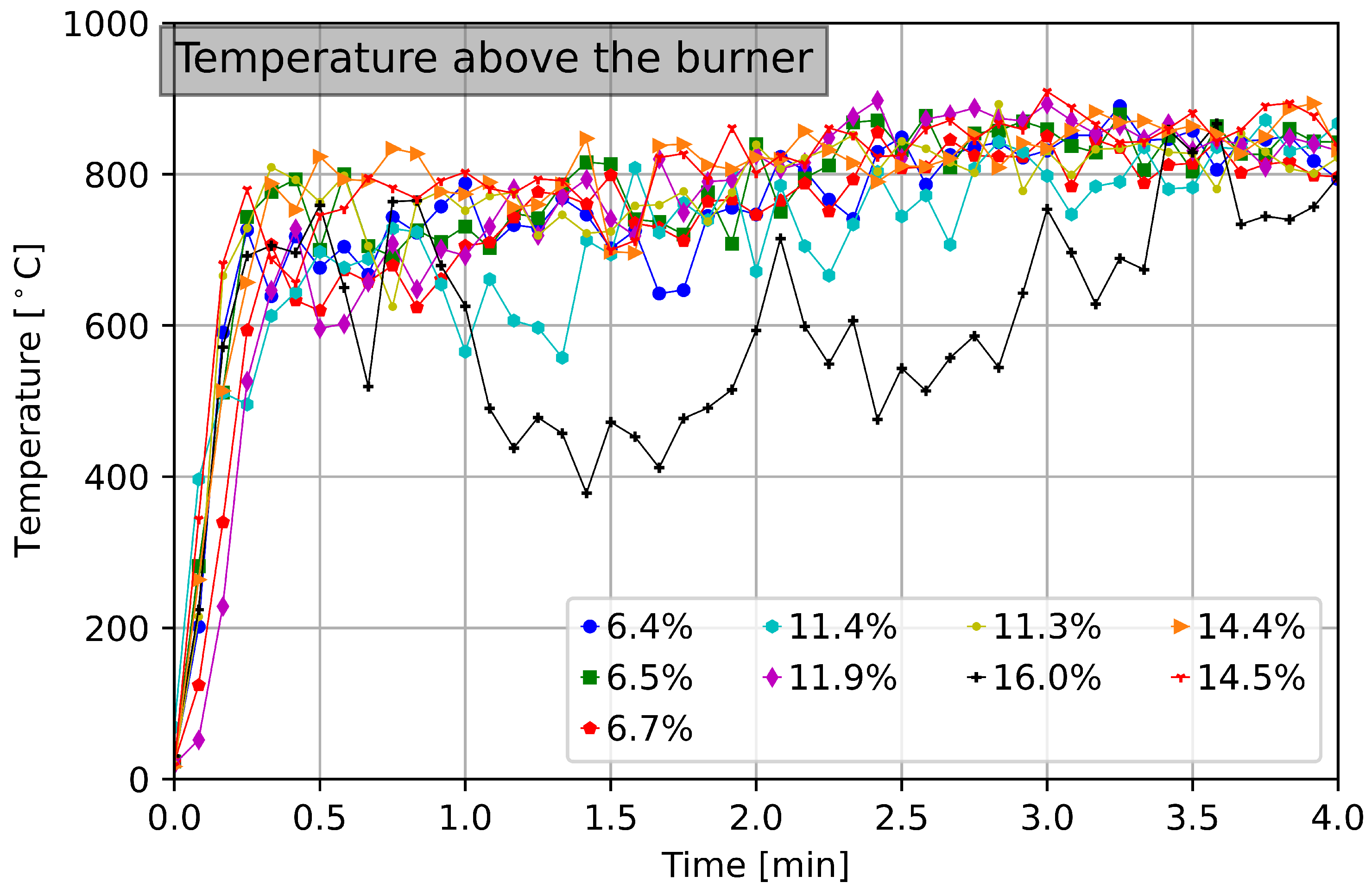
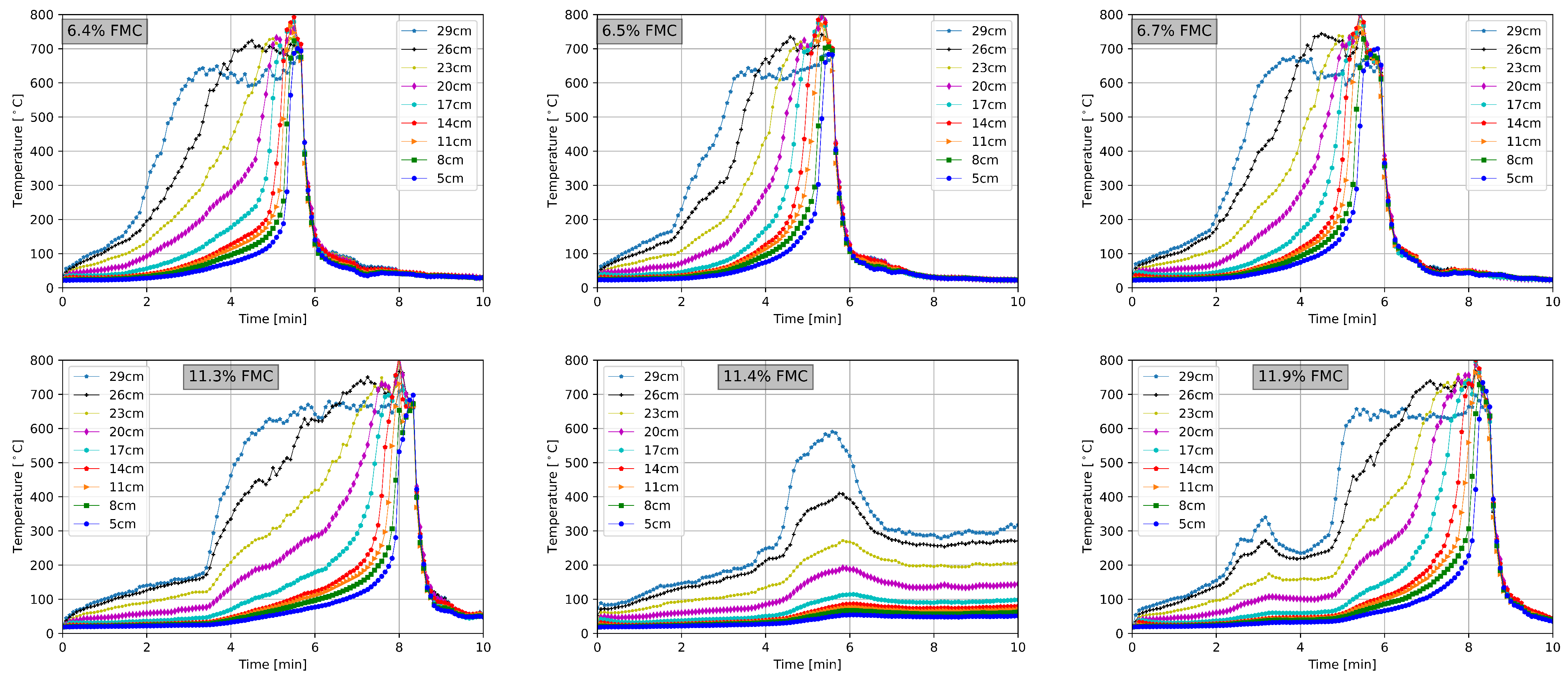
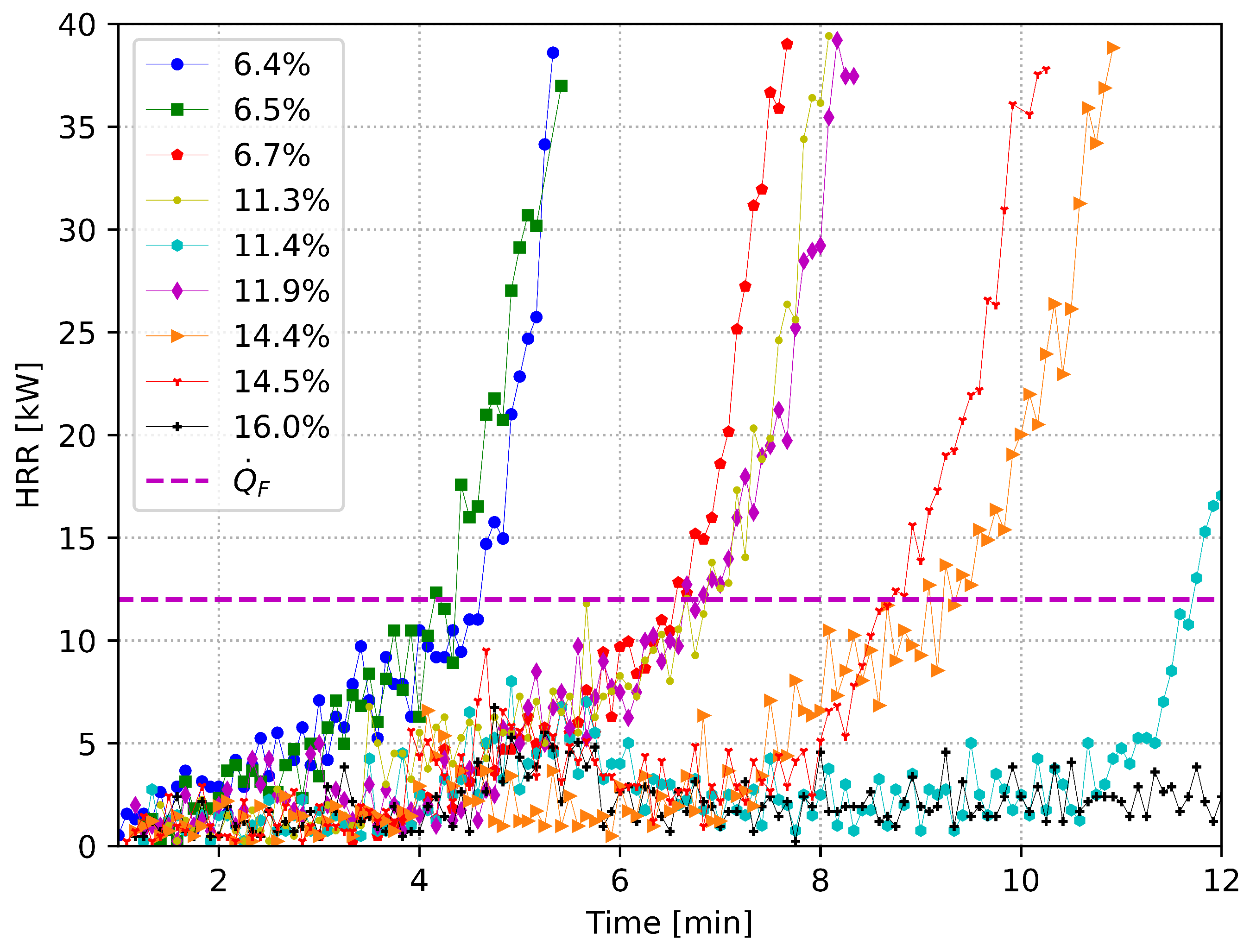
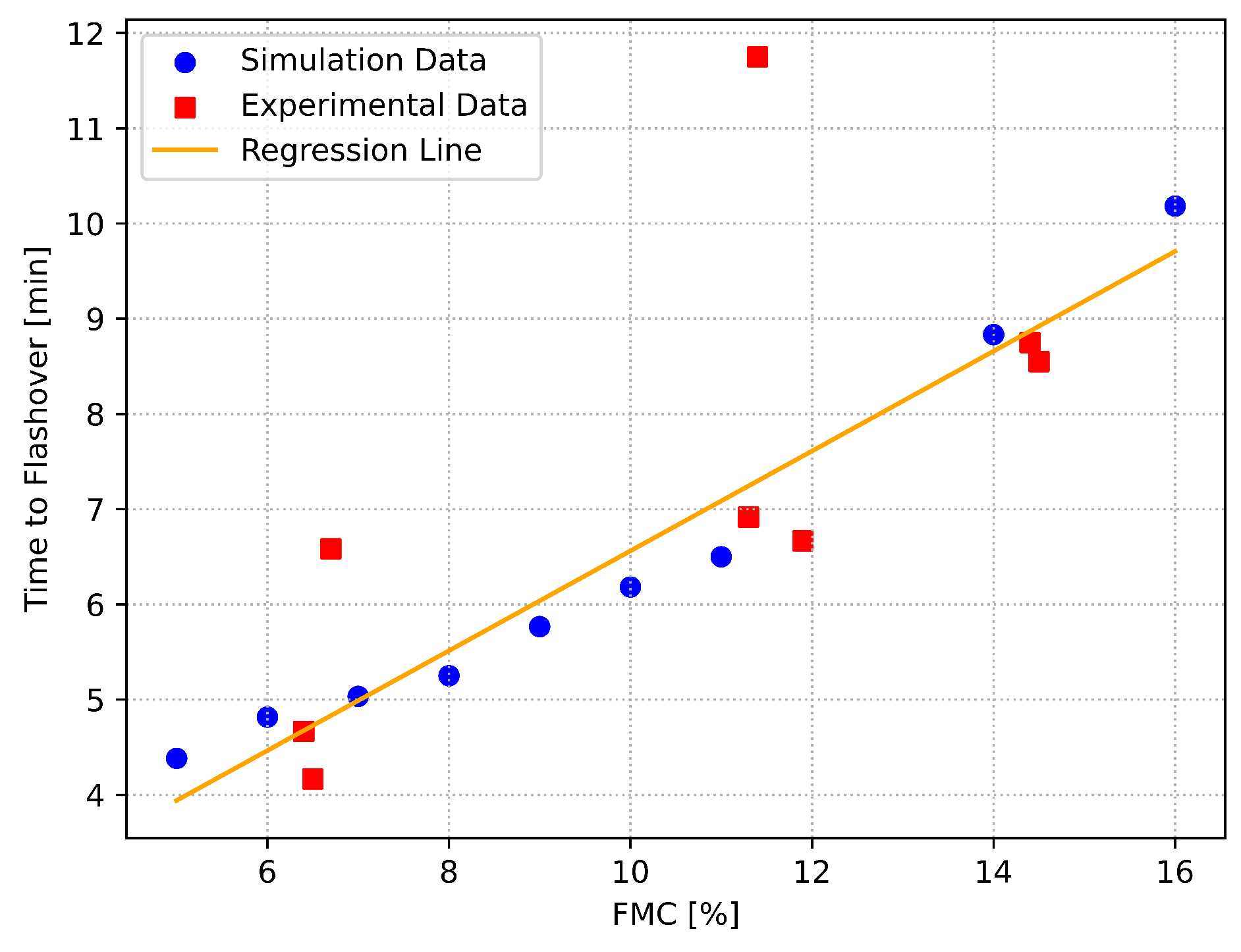
3. Experimental Results and Discussion
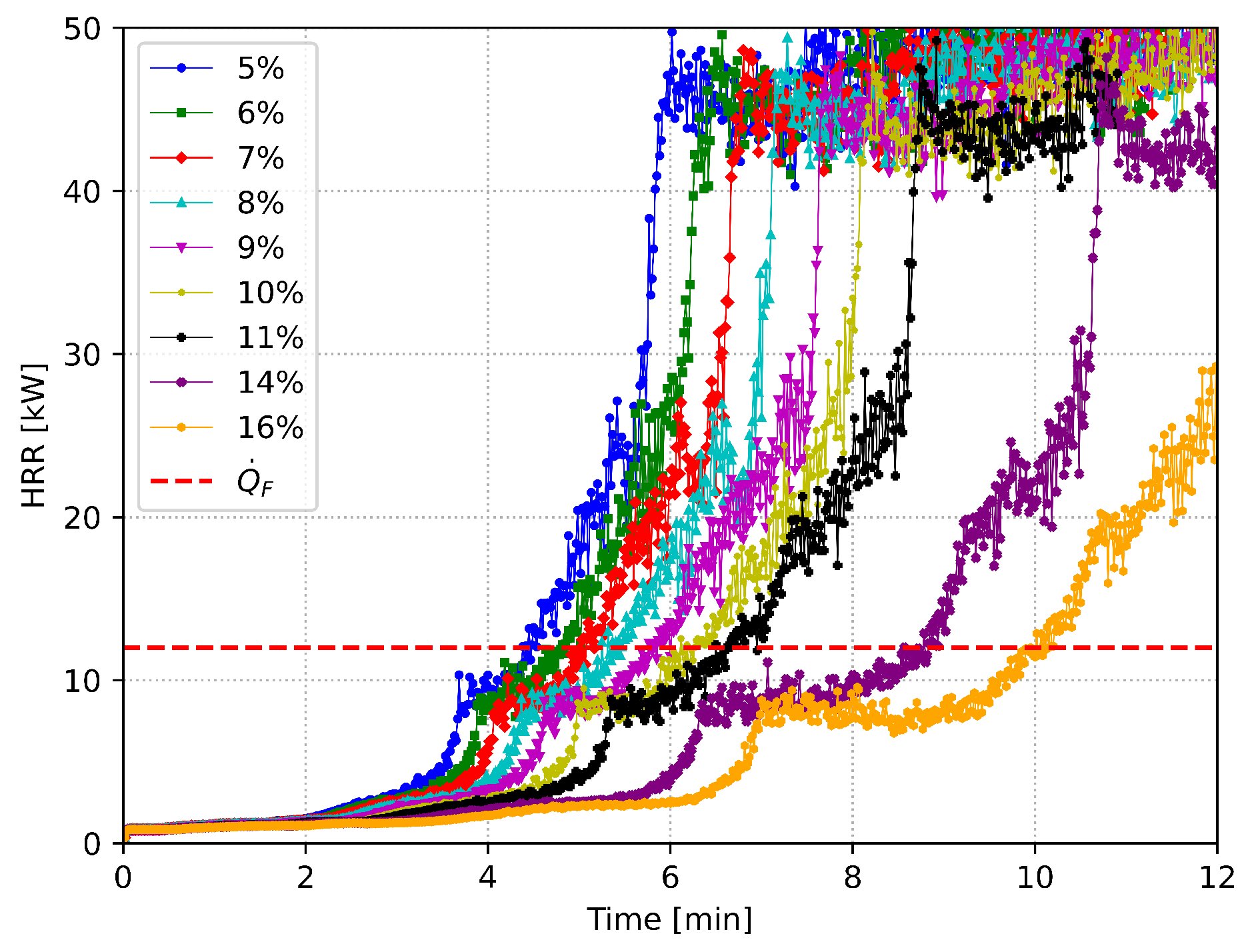
4. Numerical Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mock, C.; Peck, M.; Juillard, C.; Meddings, D.; Gielen, A.; McKenzie, L. Burn Prevention: Success Stories and Lessons Learned; World Health Organization: Geneva, Switzerland, 2011. [Google Scholar]
- Brushlinsky, N.; Sokolov, S.; Wagner, P.; Messerschmidt, B. World Fire Statistics, Report 27; CTIF (Comité Technique International de Prevention et d’Extinction de Feu): Paris, France, 2022. [Google Scholar]
- Log, T. Indoor relative humidity as a fire risk indicator. Build. Environ. 2017, 111, 238–248. [Google Scholar] [CrossRef]
- Log, T. Cold climate fire risk; A case study of the Lærdalsøyri Fire, January 2014. Fire Technol. 2016, 52, 1825–1843. [Google Scholar] [CrossRef]
- Losnegård, G. Norske Ulykker og Katastrofar (Norwegian Accidents and Disasters); Skald: Leikanger, Norway, 2013. [Google Scholar]
- Himoto, K.; Shinohara, M.; Sekizawa, A.; Takanashi, K.I.; Saiki, H. A field experiment on fire spread within a group of model houses. Fire Saf. J. 2018, 96, 105–114. [Google Scholar] [CrossRef]
- Pirsko, A.R.; Fons, W.L. Frequency of Urban Building Fires as Related to Daily Weather Conditions; Interim Technical Report AFSWP-866; Division of Fire Research, Forest Service, U.S. Department of Agriculture: Washington, DC, USA, 1956.
- Log, T.; Vandvik, V.; Velle, L.G.; Metallinou, M.M. Reducing Wooden Structure and Wildland-Urban Interface Fire Disaster Risk through Dynamic Risk Assessment and Management. Appl. Syst. Innov. 2020, 3, 16. [Google Scholar] [CrossRef]
- Stokkenes, S.; Strand, R.; Kristensen, L.; Log, T. Validation of a Predictive Fire Risk Indication Model using Cloud-based Weather Data Services. Procedia Comput. Sci. 2021, 184, 186–193. [Google Scholar] [CrossRef]
- Strand, R.D.; Log, T. A Cold Climate Wooden Home and Conflagration Danger Index: Justification and Practicability for Norwegian Conditions. Fire 2023, 6, 377. [Google Scholar] [CrossRef]
- Kristoffersen, M.; Log, T. Experience gained from 15 years of fire protection plans for Nordic wooden towns in Norway. Saf. Sci. 2022, 146, 105535. [Google Scholar] [CrossRef]
- Challands, N. The relationships between fire service response time and fire outcomes. Fire Technol. 2010, 46, 665–676. [Google Scholar] [CrossRef]
- Metallinou, M.M.; Log, T. Cold Climate Structural Fire Danger Rating System? Challenges 2018, 9, 12. [Google Scholar] [CrossRef]
- Drysdale, D. An Introduction to Fire Dynamics; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Khattri, S.; Log, T.; Kraaijeveld, A. A novel representation of the critical ventilation velocity for mitigating tunnel fires. Tunn. Undergr. Space Technol. 2021, 112, 103853. [Google Scholar] [CrossRef]
- Kraaijeveld, A.; Gunnarshaug, A.; Schei, B.; Log, T. Burning Rate and Time to Flashover in Wooden ¼ scale Compartments as a Function of Fuel Moisture Content. In Proceedings of the 8th International Fire Science & Engineering Conference, Windsor, UK, 4–6 July 2016. [Google Scholar]
- Mozaffari, M.H.; Li, Y.; Ko, Y. Real-time detection and forecast of flashovers by the visual room fire features using deep convolutional neural networks. J. Build. Eng. 2023, 64, 105674. [Google Scholar] [CrossRef]
- Caton, S.E.; Hakes, R.S.; Gorham, D.J.; Zhou, A.; Gollner, M.J. Review of pathways for building fire spread in the wildland urban interface part I: Exposure conditions. Fire Technol. 2017, 53, 429–473. [Google Scholar] [CrossRef]
- Cicione, A.; Walls, R.S.; Kahanji, C. Experimental study of fire spread between multiple full scale informal settlement dwellings. Fire Saf. J. 2019, 105, 19–27. [Google Scholar] [CrossRef]
- Moradi, A. A Physics-Based Model for Fire Spreading in Low Cost Housing in South African; Stellenbosch University: Stellenbosch, South Africa, 2016. [Google Scholar]
- Hurley, M.J.; Gottuk, D.T.; Hall, J.R., Jr.; Harada, K.; Kuligowski, E.D.; Puchovsky, M.; Torero, J.; Watts, J.M., Jr.; Wieczorek, C.J. SFPE Handbook of Fire Protection Engineering; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Lock, A.; Bundy, M.; Johnsson, E.L.; Hamins, A.; Ko, G.H.; Hwang, C.; Fuss, P.; Harris, R. Experimental study of the effects of fuel type, fuel distribution, and vent size on full-scale underventilated compartment fires in an ISO 9705 room. NIST Tech. Note 2008, 1603, 53–54. [Google Scholar]
- Vabø, M.M. Analysis of Wood Fuel Moisture Content on Enclosure Fire through Small Scale Experiments. Master’s Thesis, Western Norway University of Applied Sciences, Haugesund, Norway, 2021. [Google Scholar]
- Simpson, W.T. Equilibrium Moisture Content of Wood in Outdoor Locations in the United States and Worldwide; Technical Report; U.S. Department of Agriculture: Washington, DC, USA, 1998. [CrossRef]
- Aniszewska, M.; Gendek, A. Comparison of heat of combustion and calorific value of the cones and wood of selected forest trees species. For. Res. Pap. 2014, 75. [Google Scholar] [CrossRef]
- KERN; SOHN. Platform Scales. 2023. Available online: https://www.kern-sohn.com/shop/en/industrial-scales/platform-scales/ (accessed on 10 March 2023).
- Babrauskas, V.; Peacock, R.D.; Reneke, P.A. Defining flashover for fire hazard calculations: Part II. Fire Saf. J. 2003, 38, 613–622. [Google Scholar] [CrossRef]
- Hägglund, B. Estimating flashover potential in residential rooms. FOA Rapp. C 1980, 202369, A3. [Google Scholar]
- Babrauskas, V. Estimating room flashover potential. Fire Technol. 1980, 16, 94–103. [Google Scholar] [CrossRef]
- Thomas, P.H. Testing products and materials for their contribution to flashover in rooms. Fire Mater. 1981, 5, 103–111. [Google Scholar] [CrossRef]
- McCaffrey, B.; Quintiere, J.; Harkleroad, M. Estimating room temperatures and the likelihood of flashover using fire test data correlations. Fire Technol. 1981, 17, 98–119. [Google Scholar] [CrossRef]
- Melcher, T.; Zinke, R.; Trott, M.; Krause, U. Experimental investigations on the repeatability of real scale fire tests. Fire Saf. J. 2016, 82, 101–114. [Google Scholar] [CrossRef]
- McDermott, R.; McGrattan, K.; Hostikka, S. Fire dynamics simulator (version 5) technical reference guide. NIST Spec. Publ. 2008, 1018, 5. [Google Scholar]
- McGrattan, K.; Hostikka, S.; McDermott, R.; Floyd, J.; Weinschenk, C.; Overholt, K. Fire dynamics simulator technical reference guide volume 1: Mathematical model. NIST Spec. Publ. 2013, 1018, 175. [Google Scholar]
- Rinta-Paavola, A.; Hostikka, S. A model for the pyrolysis of two Nordic structural timbers. Fire Mater. 2022, 46, 55–68. [Google Scholar] [CrossRef]
- Wang, X. Fire Dynamics Simulator (FDS) Pyrolysis Model Analysis of Heavy Goods Vehicle Fires in Road Tunnels. Ph.D Thesis, University of Canterbury, Christchurch, New Zealand, 2017. [Google Scholar]
- Beji, T.; Merci, B. Numerical simulations of a full-scale cable tray fire using small-scale test data. Fire Mater. 2019, 43, 486–496. [Google Scholar] [CrossRef]
- Lannon, C.M.; Stoliarov, S.I.; Lord, J.M.; Leventon, I.T. A methodology for predicting and comparing the full-scale fire performance of similar materials based on small-scale testing. Fire Mater. 2018, 42, 710–724. [Google Scholar] [CrossRef]
- Suh, H.W.; Im, S.M.; Park, T.H.; Kim, H.J.; Kim, H.S.; Choi, H.K.; Chung, J.H.; Bae, S.C. Fire spread of thermal insulation materials in the ceiling of piloti-type structure: Comparison of numerical simulation and experimental fire tests using small-and real-scale models. Sustainability 2019, 11, 3389. [Google Scholar] [CrossRef]



| Combustion Efficiency () | Heat of Combustion | Density | Asymptotic Burning Rate () | Empirical Constant () |
|---|---|---|---|---|
| 0.993 | 719 | 40 |
| Burner Size | Methanol | Time | Mass Loss Rate | HRR |
|---|---|---|---|---|
| (mm) | (g) | (min:s) | (g/s) | (kW) |
| 55 × 55 | 26.7 | 10:07 | 0.043 | 0.85 |
| 55 × 55 | 29 | 11:32 | 0.042 | 0.83 |
| 55 × 55 | 33 | 12:44 | 0.043 | 0.85 |
| Thermocouple (center of room) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Height from floor (cm) | 5 | 8 | 11 | 14 | 17 | 20 | 23 | 26 | 29 |
| Thermocouple (center of door) | 10 | 11 | 12 | 13 | |||||
| Height from the floor (cm) | 1 | 13 | 15 | 24 |
| MATL ID | Dry Wood | Char | Moisture |
|---|---|---|---|
| Specific heat | 2.85 | 1.6 | 4.148 |
| Conductivity | 0.14 | 0.09 | 0.6 |
| Density | 640.0 | 200.0 | 1000.0 |
| Heat of combustion | - | - | |
| N Reactions | 1 | - | 1 |
| Heat of reaction | 300.0 | - | 2200.0 |
| NU MATL (1,1) | - | 0.15 | - |
| SPEC ID (1,1) | “REAC_FUEL” | - | “WATER VAPOR” |
| NU SPEC (1,1) | 0.85 | - | 1.0 |
| Reference temperature | 300.0 | - | - |
| A | - | - | |
| E | - | - |
| SURF ID | “Wet Wood” |
| Backing | “VOID” |
| MATL ID (1, 1:2) | “Dry Wood”, “Moisture” |
| MATL MASS FRACTION (1, 1:2) | 0.85, 0.15 |
| Thickness (1) | 0.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khattri, S.K.; Log, T.; Kraaijeveld, A. Influence of Wooden Compartment’s Fuel Moisture Content on Time to Flashover: An Experimental and Numerical Study. Fire 2024, 7, 17. https://doi.org/10.3390/fire7010017
Khattri SK, Log T, Kraaijeveld A. Influence of Wooden Compartment’s Fuel Moisture Content on Time to Flashover: An Experimental and Numerical Study. Fire. 2024; 7(1):17. https://doi.org/10.3390/fire7010017
Chicago/Turabian StyleKhattri, Sanjay Kumar, Torgrim Log, and Arjen Kraaijeveld. 2024. "Influence of Wooden Compartment’s Fuel Moisture Content on Time to Flashover: An Experimental and Numerical Study" Fire 7, no. 1: 17. https://doi.org/10.3390/fire7010017








