Theoretical Prediction Model of the Explosion Limits for Multi-Component Gases (Multiple Combustible Gases Mixed with Inert Gases) under Different Temperatures
Abstract
:1. Introduction
2. Materials and Methods
2.1. Prediction Model of Lower Explosion Limit of Two Combustible Gases Mixed with Inert Gas at Different Temperatures
2.2. Prediction Model of the Lower Explosion Limit of Multiple Combustible Gases Mixed with Inert Gases at Different Temperatures
3. Results
3.1. Model Verification
3.2. Analysis
4. Discussion
5. Conclusions
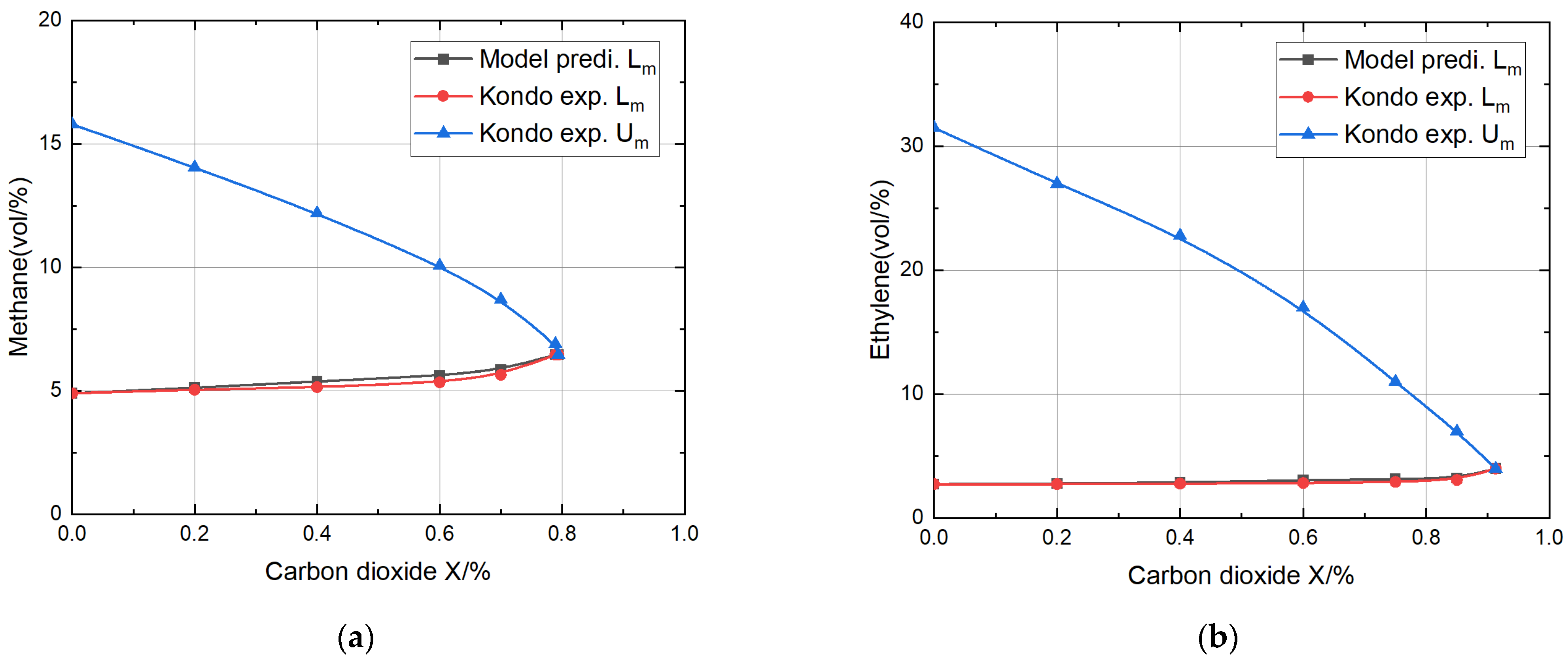
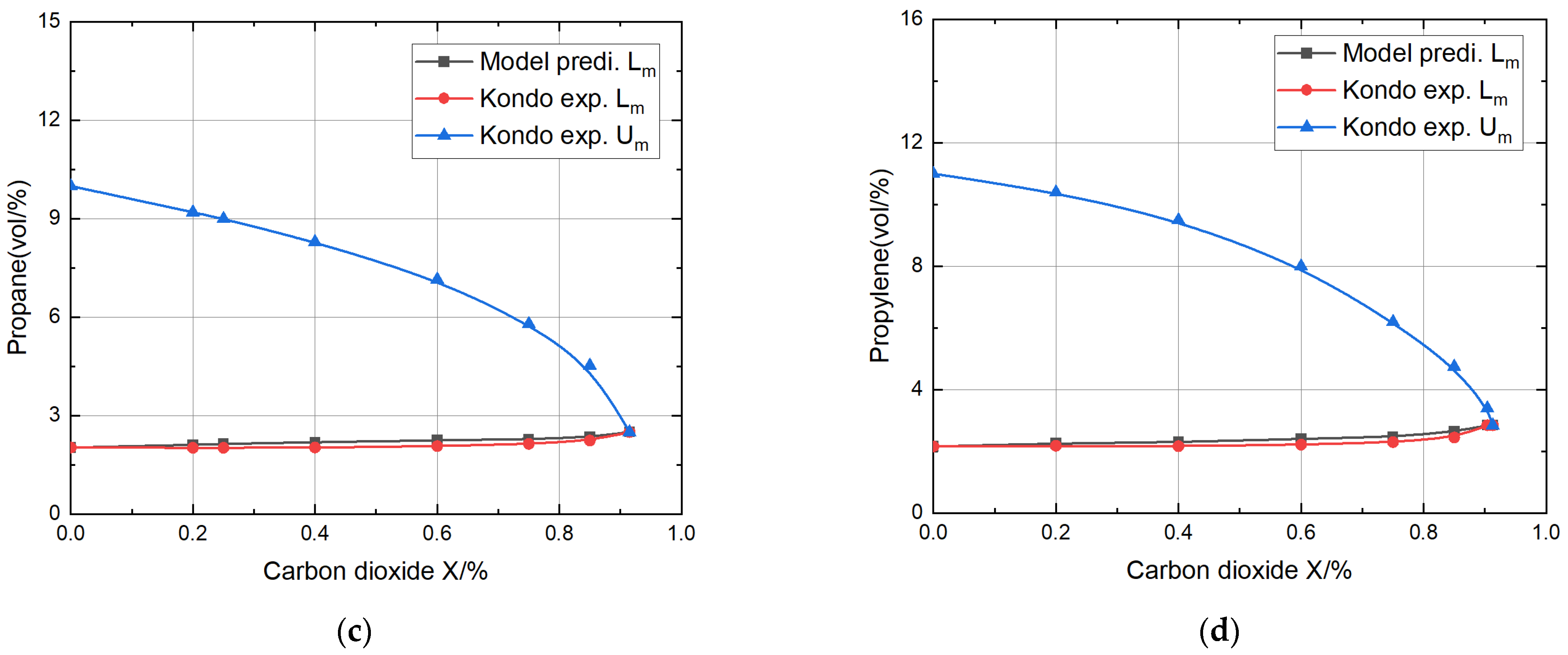
- The relative errors are all less than 8% when the proportion of inert gas is less than 70%, and the model’s accuracy was fully verified. Due to the higher specific heat of CO2 compared to N2, and the fact that CO2 directly participates in chemical reactions and thermal radiation, the theoretical model predicted that the CO2 dilution effect was better than that of N2, and the error was somewhat smaller.
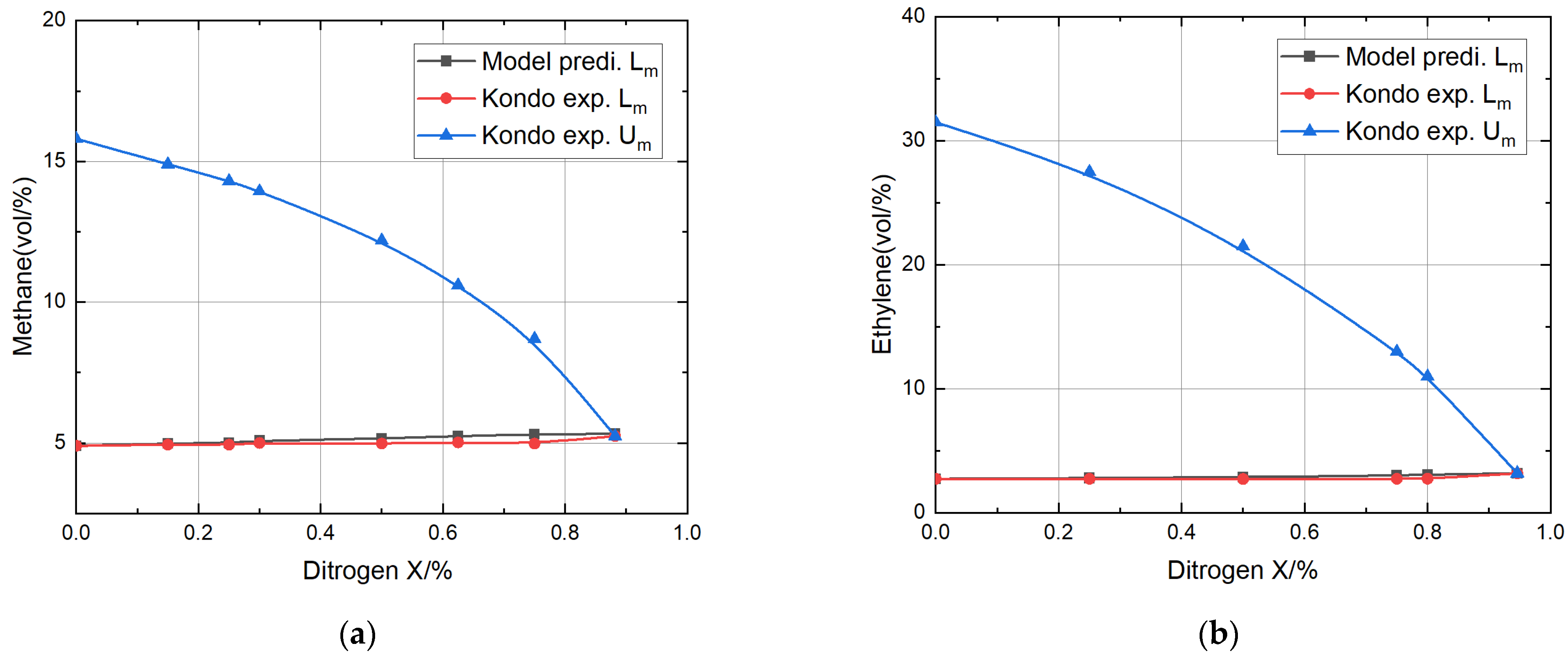
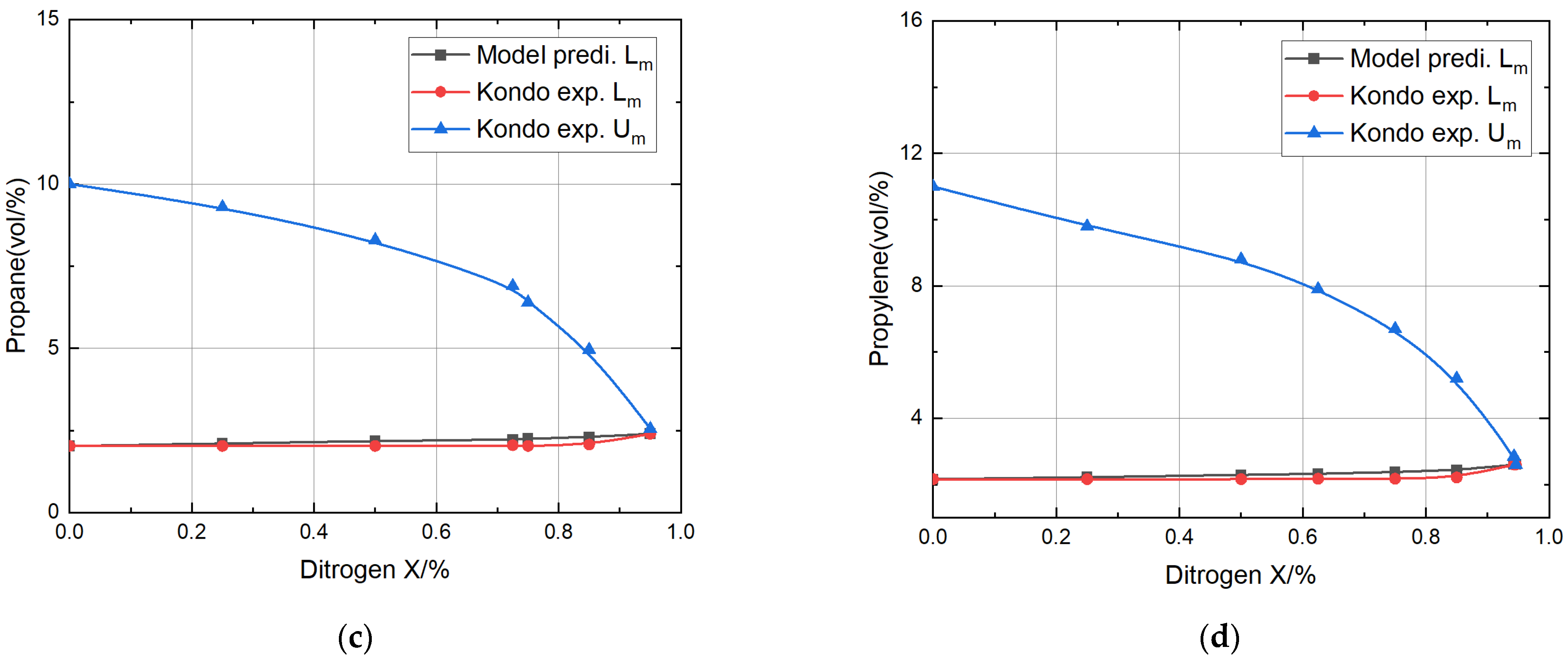
- Comparing the predicted explosion limits of four different combustible gases mixed with nitrogen with the experimental values, it was found that the relative error for the methane mixture was the smallest, at only 2.66% and 3.24%, respectively; the relative error for the propane mixture was the largest, reaching 6.82% and 6.19%, respectively.
- The theoretical model’s predictions for the lower explosion limits for methane, ethylene, propane, and propylene mixtures with nitrogen or carbon dioxide fell within the acceptable range of relative error compared to the experimental values of Kondo, thoroughly verifying the validity of the theoretical model.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| L | Lower explosive limit of the fuel | |
| D | Inert gas | |
| ∆Hc | Heat of combustion | kJ/mol |
| ∆H | Enthalpy change | J |
| ∆Hc,j | Heat of combustion of the reactants | J |
| Standard heat of combustion for 1 mole of fuel at 298 K | J | |
| The specific heat capacity of the reactants | J∙g−1K−1 | |
| Qr | Heat loss | J |
| a | Surface radiant heat transfer coefficient | W/(m2K) |
| e | Radiance | |
| As | Heat exchange surface area per mole of mixture | m2/mol |
| σ | Stefan–Boltzmann constant | W/(m2·K4) |
| Δt | Flame propagation duration | S |
| Φ | Radiation flux density | |
| Ti | Initial temperature | K |
| TL | Flame temperature of LFL | K |
| n | Chemical reaction order |
References
- Hao, Y.; Peizhi, W.; Xiangyun, W. Current situation and Influencing Factors of Gas and dust explosion accidents in China. Saf. Environ. Eng. 2008, 15, 97–99. [Google Scholar] [CrossRef]
- Bond, J. Sources of Ignition: Flammability Characteristics of Chemicals and Products; Butterworth-Heinemann: Oxford, UK, 1991; pp. 147–151. [Google Scholar]
- Lian, P.; Gao, X.; Mannan, M.S. Prediction of minimum ignition energy of aerosols using flame kernel modeling combined with flame front propagation theory. J. Loss Prevent. Proc. 2012, 25, 103–113. [Google Scholar] [CrossRef]
- Chen, T.; HU, S. Research progress of combustible gas explosion process. Sci. Technol. Inf. Dev. Econ. 2006, 16, 171–172. [Google Scholar] [CrossRef]
- Tian, G.; Ma, Y.; Yang, Z.; Feng, Y.; Wang, Z. Theoretical and Experimental Study on explosion Limit and Suppression of Combustible Refrigerant. J. Shandong Inst. Civ. Eng. Archit. 2001, 16, 58–63. [Google Scholar] [CrossRef]
- Barbosa, J.A.; Coronado, C.; Tuna, C.E.; Silva, M.H.; Mendiburu, A.Z.; Junior, J.; de Andrade, J.C. Experimental determination of lower flammability limits of Synthesized Iso-Paraffins (SIP), jet fuel and mixtures at atmospheric and reduced pressures with air. Fire Saf. J. 2021, 121, 103276. [Google Scholar] [CrossRef]
- Zhang, K.; Luo, T.; Li, Y.; Zhang, T.; Li, X.; Zhang, Z.; Shang, S.; Zhou, Y.; Zhang, C.; Chen, X.; et al. Effect of ignition, initial pressure and temperature on the lower flammability limit of hydrogen/air mixture. Int. J. Hydrogen Energy 2022, 47, 15107–15119. [Google Scholar] [CrossRef]
- Markus, D.; Schildberg, H.P.; Wildner, W.; Krdzalic, G.; Maas, U. Flammability limits of premixed methane/methanol/air flames. Combust. Sci. Technol. 2003, 175, 2095–2112. [Google Scholar] [CrossRef]
- Chen, X.; Bi, S.; Wu, J. Experimental study on explosion limit of dimethyl ether, methane and dimethyl ether/methane mixtures. J. Eng. Thermophys.-Rus. 2009, 30, 1267–1270. [Google Scholar] [CrossRef]
- Zabetakis, M.G. Flammability Characteristics of Combustion Gases and Vapors. US Bureau of Mines: Washington, DC, USA, 1965; pp. 97–107. [Google Scholar]
- Kondo, S.; Takizawa, K.; Takahashi, A.; Tokuhashi, K. On the temperature dependence of flammability limits of gases. J. Hazard. Mater. 2011, 187, 585–590. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Yang, X.; Lu, L.; Wang, X. Determination of explosion limit of alkanes at high temperature. Chem. Ind. Prog. 2002, 21, 496–498. [Google Scholar] [CrossRef]
- Besnard, S. Full Flammability Test of Gases and Gas Mixtures in Air; CERN: Meyrin, Switzerland, 1996; pp. 253–258. [Google Scholar]
- Li, S.; Zhang, Y.; Qiu, X.; Li, B.; Zhang, H. Effects of Inert Dilution and Preheating Temperature on Lean Flammability Limit of Syngas. Energ. Fuels 2014, 28, 3442–3452. [Google Scholar] [CrossRef]
- Hu, X.; Yu, Q.; Sun, N.; Qin, Q. Experimental study of flammability limits of oxy-methane mixture and calculation based on thermal theory. Int. J. Hydrogen Energy 2014, 39, 9527–9533. [Google Scholar] [CrossRef]
- Hu, X.; Xie, Q.; Yu, Q.; Liu, H.; Yan, F. Effect of Carbon Dioxide on the Lower Flammability Limit of Propane in O2/CO2 Atmosphere. Energ. Fuels 2020, 34, 4993–4998. [Google Scholar] [CrossRef]
- Hu, X.; Xie, Q.; Zhang, J.; Yu, Q.; Liu, H.; Sun, Y. Experimental study of the lower flammability limits of H2/O2/CO2 mixture. Int. J. Hydrogen Energy 2020, 45, 27837–27845. [Google Scholar] [CrossRef]
- Rowley, J.R.; Rowley, R.L.; Wilding, W.V. Estimation of the lower flammability limit of organic compounds as a function of temperature. J. Hazard. Mater. 2011, 186, 551–557. [Google Scholar] [CrossRef] [PubMed]
- Albahri, T.A. Flammability characteristics of pure hydrocarbons. Chem. Eng. Sci. 2003, 58, 3629–3641. [Google Scholar] [CrossRef]
- Albahri, T.A. Prediction of the lower flammability limit percent in air of pure compounds from their molecular structures. Fire Saf. J. 2013, 59, 188–201. [Google Scholar] [CrossRef]
- Vidal, M.; Wong, W.; Rogers, W.J.; Mannan, M.S. Evaluation of lower flammability limits of fuel–air–diluent mixtures using calculated adiabatic flame temperatures. J. Hazard. Mater. 2006, 130, 21–27. [Google Scholar] [CrossRef]
- Kondo, S.; Urano, Y.; Tokuhashi, K.; Takahashi, A.; Tanaka, K. Prediction of flammability of gases by using F-number analysis. J. Hazard. Mater. 2001, 82, 113–128. [Google Scholar] [CrossRef]
- Shebeko, Y.N.; Fan, W.; Bolodian, I.A.; Navzenya, V.Y. An analytical evaluation of flammability limits of gaseous mixtures of combustible–oxidizer–diluent. Fire Saf. J. 2002, 37, 549–568. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Z.; Xu, J.; Liu, H.; Hou, P.; He, L. Analysis of combustion characteristics and thermal characteristics of different gas fuels. Econ. Energy 2022, 41, 15–19. [Google Scholar] [CrossRef]
- Cui, S.; Sun, B.; Sun, X. General formula for the radiative brightness response of black bodies in the infrared band. Spectrosc. Spect. Anal. 2020, 40, 1329–1333. [Google Scholar] [CrossRef]
- Kondo, S.; Takizawa, K.; Takahashi, A.; Tokuhashi, K. Extended Le Chatelier’s formula and nitrogen dilution effect on the flammability limits. Fire Saf. J. 2006, 41, 406–417. [Google Scholar] [CrossRef]
- Kondo, S.; Takizawa, K.; Takahashi, A.; Tokuhashi, K. Extended Le Chatelier’s formula for carbon dioxide dilution effect on flammability limits. J. Hazard. Mater. 2006, 138, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Kondo, S.; Takizawa, K.; Takahashi, A.; Tokuhashi, K.; Sekiya, A. Flammability limits of isobutane and its mixtures with various gases. J. Hazard. Mater. 2007, 148, 640–647. [Google Scholar] [CrossRef] [PubMed]
- Poling, B.E.; Prausnitz, J.M.; Connell, J.P. The Properties of Gases and Liquids, 5th ed.; McGraw-Hill: New York, NY, USA, 2001; pp. 133–149. [Google Scholar]
- Dippro, A. DIPPR Project 801 Pure Component Data; Public Version; American Institute of Chemical Engineers: New York, NY, USA, 1996; pp. 209–233. [Google Scholar]
- Ma, T. Using critical flame temperature for estimating lower flammable limits of a mixture. Process Saf. Prog. 2013, 32, 387–392. [Google Scholar] [CrossRef]

| Compound | Mole Fraction before Combustion | Mole Fraction after Combustion |
|---|---|---|
| 0 | ||
| 0 | ||
| Inert gas | ||
| Nitrogen | ||
| Oxygen | ||
| Carbon dioxide | 0 | |
| Water | 0 |
| Gas Mixture | Inert Gas Ratio X/% | Poling TL/K | DIPPR TL/K | Model Prediction Lm | Kondo Experiment Lm | Relative Error/% | Kondo Experiment Um |
|---|---|---|---|---|---|---|---|
| Methane + Nitrogen | 0 | 1264 | 1264 | 4.90 | 4.90 | 0 | 15.8 |
| 0.15 | 4.98 | 4.94 | 0.8 | 14.9 | |||
| 0.25 | 5.01 | 4.94 | 1.4 | 14.3 | |||
| 0.30 | 5.08 | 5.00 | 1.6 | 13.94 | |||
| 0.50 | 5.16 | 4.98 | 3.6 | 12.19 | |||
| 0.625 | 5.25 | 5.02 | 4.6 | 10.6 | |||
| 0.75 | 5.31 | 4.98 | 6.6 | 8.7 | |||
| Ethylene + Nitrogen | 0 | 1209 | 1209 | 2.74 | 2.74 | 0 | 31.5 |
| 0.25 | 2.80 | 2.74 | 2.2 | 25.0 | |||
| 0.50 | 2.89 | 2.73 | 5.9 | 18.4 | |||
| 0.75 | 3.01 | 2.74 | 9.8 | 10.5 | |||
| 0.80 | 3.08 | 2.75 | 12 | 7.0 | |||
| Propane + Nitrogen | 0 | 1287 | 1287 | 2.03 | 2.03 | 0 | 10.0 |
| 0.25 | 2.10 | 2.03 | 3.3 | 9.1 | |||
| 0.50 | 2.18 | 2.03 | 7.4 | 8.2 | |||
| 0.725 | 2.22 | 2.05 | 8.3 | 7.53 | |||
| 0.75 | 2.25 | 2.03 | 10.8 | 6.4 | |||
| 0.85 | 2.30 | 2.07 | 11.1 | 4.96 | |||
| Propylene + Nitrogen | 0 | 1294 | 1294 | 2.16 | 2.16 | 0 | 11.0 |
| 0.25 | 2.22 | 2.16 | 2.8 | 9.8 | |||
| 0.50 | 2.29 | 2.16 | 6 | 8.8 | |||
| 0.625 | 2.32 | 2.17 | 6.9 | 7.9 | |||
| 0.75 | 2.38 | 2.17 | 9.6 | 6.7 | |||
| 0.85 | 2.43 | 2.21 | 9.95 | 5.2 | |||
| Methane + Carbon dioxide | 0 | 1264 | 1264 | 4.9 | 4.90 | 0 | 15.8 |
| 0.20 | 5.13 | 5.05 | 1.6 | 14.06 | |||
| 0.40 | 5.38 | 5.15 | 4.3 | 12.2 | |||
| 0.60 | 5.62 | 5.35 | 4.8 | 10.08 | |||
| 0.70 | 5.86 | 5.65 | 5.5 | 8.7 | |||
| Ethylene + Carbon dioxide | 0 | 1209 | 1209 | 2.74 | 2.74 | 0 | 31.5 |
| 0.20 | 2.79 | 2.74 | 1.8 | 24.1 | |||
| 0.40 | 2.87 | 2.77 | 3.6 | 18.5 | |||
| 0.60 | 3.04 | 2.83 | 7.4 | 12.75 | |||
| 0.75 | 3.15 | 2.92 | 7.9 | 8.8 | |||
| 0.85 | 3.23 | 3.08 | 10.1 | 6.03 | |||
| Propane + Carbon dioxide | 0 | 1287 | 1287 | 2.03 | 2.03 | 0 | 10 |
| 0.20 | 2.11 | 2.02 | 4.5 | 9.2 | |||
| 0.25 | 2.14 | 2.02 | 5.9 | 8.9 | |||
| 0.40 | 2.19 | 2.03 | 7.9 | 8.3 | |||
| 0.60 | 2.25 | 2.07 | 8.7 | 7.15 | |||
| 0.75 | 2.28 | 2.14 | 6.5 | 5.8 | |||
| 0.85 | 2.35 | 2.24 | 9.8 | 4.53 | |||
| Propylene + Carbon dioxide | 0 | 1294 | 1294 | 2.16 | 2.16 | 0 | 11 |
| 0.20 | 2.26 | 2.18 | 3.7 | 9.7 | |||
| 0.40 | 2.30 | 2.17 | 6.0 | 8.8 | |||
| 0.60 | 2.41 | 2.22 | 8.6 | 7.35 | |||
| 0.75 | 2.47 | 2.30 | 7.4 | 6.13 | |||
| 0.85 | 2.64 | 2.45 | 7.8 | 4.75 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Q.; Guo, Y.; Zhong, M.; You, J.; He, Y.; Chen, J.; Zhang, Z. Theoretical Prediction Model of the Explosion Limits for Multi-Component Gases (Multiple Combustible Gases Mixed with Inert Gases) under Different Temperatures. Fire 2022, 5, 143. https://doi.org/10.3390/fire5050143
Ma Q, Guo Y, Zhong M, You J, He Y, Chen J, Zhang Z. Theoretical Prediction Model of the Explosion Limits for Multi-Component Gases (Multiple Combustible Gases Mixed with Inert Gases) under Different Temperatures. Fire. 2022; 5(5):143. https://doi.org/10.3390/fire5050143
Chicago/Turabian StyleMa, Qiuju, Yuhao Guo, Mingyu Zhong, Jingfeng You, Ya He, Jianhua Chen, and Zhaokun Zhang. 2022. "Theoretical Prediction Model of the Explosion Limits for Multi-Component Gases (Multiple Combustible Gases Mixed with Inert Gases) under Different Temperatures" Fire 5, no. 5: 143. https://doi.org/10.3390/fire5050143




