Superspreading Surfactant on Hydrophobic Porous Substrates

Abstract

The wetting behavior of droplets of aqueous surfactant solutions over hydrophobic thin PVDF porous membrane and non-porous hydrophobic PVDF film is investigated for small (~10 μL) droplets of aqueous trisiloxane surfactant solutions: superspreader S 240. The time dependencies of contact angle, droplet radius, wetted area and volume were monitored as well as penetration into the porous substrate. It is shown that the fast spreading of droplets of trisiloxane solutions takes place both in the case of porous and non-porous substrates at a concentration above some critical concentration. It was found that the trisiloxane droplets penetrate into the hydrophobic porous substrates and disappear much faster than on a corresponding hydrophobic non-porous substrate, which was not observed before. This phenomenon is referred to as “superpenetration”.

1. Introduction

Wetting, spreading and penetration of liquid droplets into porous substrates are frequent phenomena observed in natural processes and applications [1,2]. A considerable number of substrates used in applications are porous: examples are inkjet printing [3,4,5], irrigation [6,7,8], oil recovery [9,10,11], waste water purification [12], medical treatments [13], painting of exterior surfaces [14], trickle bed reactors [12], and a range of other applications [15]. The vast majority of the experimental research and theory published on wetting and spreading is focussed on smooth and homogenous substrates [16]. The basics of wetting and spreading have been studied in the case of non-porous substrates [17,18,19]. Spreading over porous substrates has been reviewed recently [19]. Surfactant solutions are frequently used in a number of applications, for example, in enhanced oil recovery to extract oil or gas. The rocks where the oil/gas is located are usually porous [20], which is one of the reasons why spreading over porous substrates attracts so much attention.

Wetting and spreading of liquids on non-porous substrates includes two competing processes that occur simultaneously: spreading and evaporation. Similarly, wetting and spreading of liquids on porous substrates also includes two competing processes that occur simultaneously: spreading and imbibition into porous substrate, but the nature of these processes is substantially different.

1.1. Stages of Spreading/Penetration over Porous Substrates

Below the thickness of the porous layer, Δ is assumed to be much smaller than the drop height, that is, Δ << h*, where h* is the scale of the drop height. The influence of the gravity is neglected (small drops, Bond number ρgL*²/γ << 1, where ρ, g, and γ are the liquid density, gravity acceleration and the liquid-air interfacial tension, respectively). That is, only capillary forces are taken into account.

The porous layer is very thin (Figure 1), and the time for saturation in the vertical direction can be neglected relative to other time scales of the process. Let us calculate the time required for a complete saturation of the porous layer in the vertical direction. According to Darcy’s equation u = (K_p/µ)(p_c/z), −Δ < z < 0; u = dz/dt, where K_p and p_c are the permeability of the porous layer and the capillary pressure, respectively, and z is the position of the liquid front inside the porous layer. The solution of the latter equation results in: Δ² = 2K_pp_ct_Δ/µ, where t is the time of the complete saturation for the porous layer in the vertical direction and, hence, t_Δ = Δ²µ/2K_pp_c. Consideration below is restricted to t > t_Δ. Estimations show that t_Δ is much less than t_sp, which is the duration of spreading [19]. Accordingly, the porous layer beneath the spreading drop (0 < r < L(t)) is always assumed to be completely saturated: it is assumed below that the liquid wets at least partially the porous material.

1.2. Partial Wetting

The characteristic feature of partial wetting is the presence of contact angle hysteresis, that is, static advancing θ_ad, and smaller static receding contact angle, θ_r [19]. Hence, the whole process of spreading imbibition of droplets over porous substrates in the case of partial wetting can be schematically presented as shown in Figure 2.

During the first stage (Figure 2) immediately after the deposition, the droplet spreads over the porous substrate until the advancing contact angle is reached. Usually, the duration of the first stage is very small as compared with other stages of spreading/imbibition, and, hence, penetration into the porous substrate during this stage can be neglected. During the second stage, the liquid from the droplet penetrates into the porous substrate, but the three-phase contact line remains pinned at the position reached after the end of the first stage. During this period, the contact angle decreases from θ_ad to θ_r. The second stage lasts until the contact angle reaches the static receding contact angle. After the static receding contact angle is reached, the final third state of spreading/imbibition starts. During this stage, the contact angle remains constant and equal to the static receding contact angle, but the radius of the droplet base decreases until the complete disappearance of the droplet, t*, caused by the imbibition into the porous substrate. Note that precisely the same stages take place in the case of droplet spreading/evaporation over non-porous substrates [19]. That is, there is a remarkable similarity between these two processes: spreading/penetration and spreading/evaporation in spite of the completely different nature of those processes.

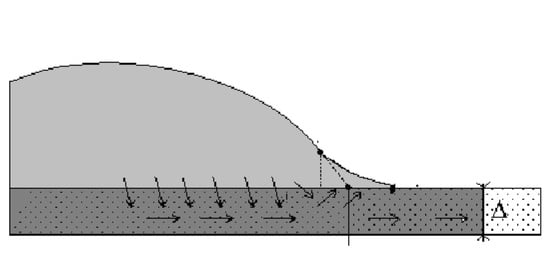
1.3. Complete Wetting Case

In the case of complete wetting, the spreading/imbibition process is substantially different from the case of partial wetting [2]. The main difference is the absence of contact angle hysteresis in the case of complete wetting. The spreading/imbibition stages in the case of complete wetting are shown in Figure 3.

Superspreaders are aqueous solutions of silicone-based non-ionic surfactants, which show superspreading behavior on hydrophobic substrates at concentrations that exceed the critical wetting concentration (CWC). The two important concentrations in the case of superspreaders are the critical aggregation concentration (CAC) and the critical wetting concentration (CWC). When the concentration of surfactants in aqueous solutions reaches the CAC, the surfactant molecules are no longer soluble and trisiloxane surfactant molecules spontaneously form dispersions of bilayer aggregates (vesicles) [21]. The most usable superspreading surfactants are trisiloxanes. Aggregates provide a supply of the trisiloxane molecules, which are necessary to support the process of superspreading [22]. Superspreaders can spread over large surface areas of hydrophobic substrates, forming in the end a film of micron thickness at concentrations above CWC. CWC represents the value of trisiloxane surfactants above which the transition from partial wetting to complete wetting is observed on some moderately hydrophobic surfaces. In all of the cases, it was found that CWC was greater than CAC [11]. CWC is very essential for herbicide delivery and in other deposition applications [22,23]. Superspreaders spread over large areas faster than pure liquids and other carbon or fluorine-based surfactants. The spreading of pure liquids in the case of complete wetting follows the power law S~t^0.2, where S is the spread area and t is time, whereas for superspreaders it is S~t [24]. There is no superspreading in dry air; therefore, humidity has an impact on the nature of superspreading [25]. Superspreaders contain a trisiloxane non-polar head group and an organic polar group. The trisiloxane surfactants used in this study have structures as shown in [16]. They have a bulky hydrophobic component, closely packed CH₃ groups, and a considerably lower air/water surface tension values than unbranched hydrocarbon surfactants [24].

Note again that, in the case of spreading/evaporation over non-porous substrates, the stages of the process are precisely the same as shown in Figure 2 [19].

2. Materials and Methods

2.1. Materials

Porous and non-porous PVDF materials with the same chemical structure were used. PVDF porous membrane was purchased from Merk Millipore Ltd. (average pore size of 0.45 µm and an average thickness of 0.01 mm), and PVDF film was purchased from GoodFellow (average thickness of 0.05 mm). Aqueous surfactant solutions were prepared using distilled water. Trisiloxane surfactant S 240 (purchased from Evonik) with critical aggregation concentration (CAC) of 0.2 g/L [25] were used. The surface tension above CAC is 22.5 mN/m S 240. S 240 is a superspreader. All solutions were used on the day when they were prepared, to avoid hydrolysis and loss of surface activity.

2.2. Contact Angle, Radius and Volume Measurements

The contact angle, spreading diameter and droplet volume were measured using the KRUSS DSA100 drop-shape analyser (Hamburg, Germany) described in [2]. It was operated via a purpose-designed ‘ADVANCE (KRUSS software, Hamburg, Germany)’ interfacial software package. The substrate is placed on the KRUSS DSA 100 table secured with double-sided tape to avoid liquid penetration under the membrane. A droplet was deposited manually on the porous (membrane) or non-porous substrate using a pipette which was set to a volume of 10 μL. The droplet was released once the droplet had contacted the substrate.

3. Results and Discussion

Preliminary experiments were carried out to prove that evaporation is negligible over the first 5 min after a droplet is deposited. A droplet of water was placed on a non-porous hydrophobic Teflon tape. The results show the decrease in volume of a droplet of water was 0.08%, which proves that evaporation is negligible. Therefore, a value of t* below or around 5 min for porous materials indicates that there is imbibition into the substrate.

3.1. Behavior of Water on PVDF Substrates

It was shown that on porous and non-porous substrates the characteristic time of complete disappearance of the pure aqueous droplet was above 3000 s, which is the time of complete evaporation of the droplet. The behavior of pure aqueous droplets on both substrates is considerably different. On porous substrates, the droplet shows complete non-wetting behavior: the droplet does not spread (the radius of the droplet base remains constant). However, on porous substrates the droplet shows partial wetting behavior (see Figure 2). Clearly, porosity influences the behavior of droplets on substrates. However, in both cases (non-porous and porous substrates) the time of the processes is more than 3000 s, that is, the kinetics is completely determined by evaporation.

3.2. S 240 on Non-Porous Hydrophobic Film of PVDF

The kinetics of the spreading of superspreader S 240 was investigated at concentrations of 0.5 CAC, 1 CAC and 2 CAC. It was shown that at a concentration of 0.5 CAC the spreading corresponds to the partial wetting regime (Figure 2). However, at concentrations of 1 CAC and 2 CAC the behavior corresponds to the complete wetting case (Figure 3). That is, the CWC is close to CAC in the case of S 240.

The kinetics of the spreading of S 240 on a hydrophobic non-porous substrate is presented in Figure 4. The initial stage of the spreading (Figure 4) is around 200 s and completely corresponds to the superspreading behavior. However, the total duration of the process is around 2000 s. That is, the tail of the process is completely determined by evaporation.

3.3. Behavior of Trisiloxane Surfactant Solutions S 240 on PVDF Membrane (Porous)

It was shown that at all concentrations of S 240 used, the initial deposition contact angles were found to be below 60°. At concentration of 0.5 CAC S 240 the droplet shows partial wetting behavior, as seen in Figure 2, while at 1 and 2 CAC the droplets show the complete wetting regime shown in Figure 3. Note, CWC is close to 1 CAC in the case under consideration.

Figure 5 shows that the duration of the process is around 500 s, that is, at least four times faster than for non-porous substrates. The process presented in Figure 5 proves that the process is completely determined by a fast penetration of the droplet inside a hydrophobic porous substrate, the process referred to as “superpenetration”. Very fast penetration into a hydrophobic porous substrate has never been found before.

4. Conclusions

It is well known that superspreader surfactants spread very fast over hydrophobic substrates. However, the complete disappearance of these penetrated droplets is caused in the end by slow evaporation. The latter could be a problem in printing, for example, where the fast disappearance of droplets from the surfaces is desirable. It is shown that complete disappearance of the droplets of superspreaders on hydrophobic porous substrate occurs very quickly, which is caused by a fast penetration of the droplets of superspreaders into the hydrophobic substrate. Spreading/imbibition of aqueous droplets of trisiloxane superspreading surfactant S 240 over a hydrophobic PVDF membrane and PVDF film were investigated. It is shown that at concentrations at or above CAC, fast spreading/penetration takes place in the case of porous hydrophobic substrates. We referee to this process as “superpenetration”.