Wettability and Adhesion Work Prediction in the Polymer–Aqueous Solution of Surface Active Agent Systems
Abstract
:1. Introduction
2. Utility Equations for the Data Treatment
3. Experimental
3.1. Materials
3.2. Methods
4. Results and Discussion
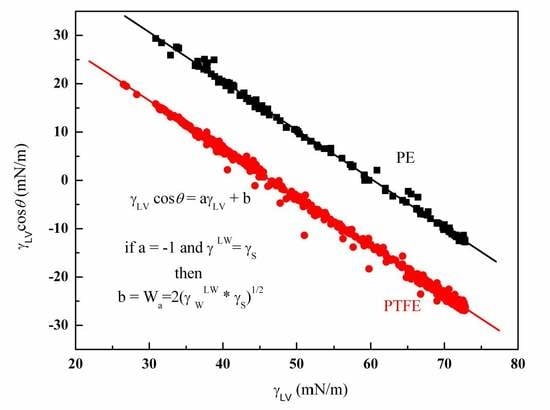
4.1. Wettability of PE
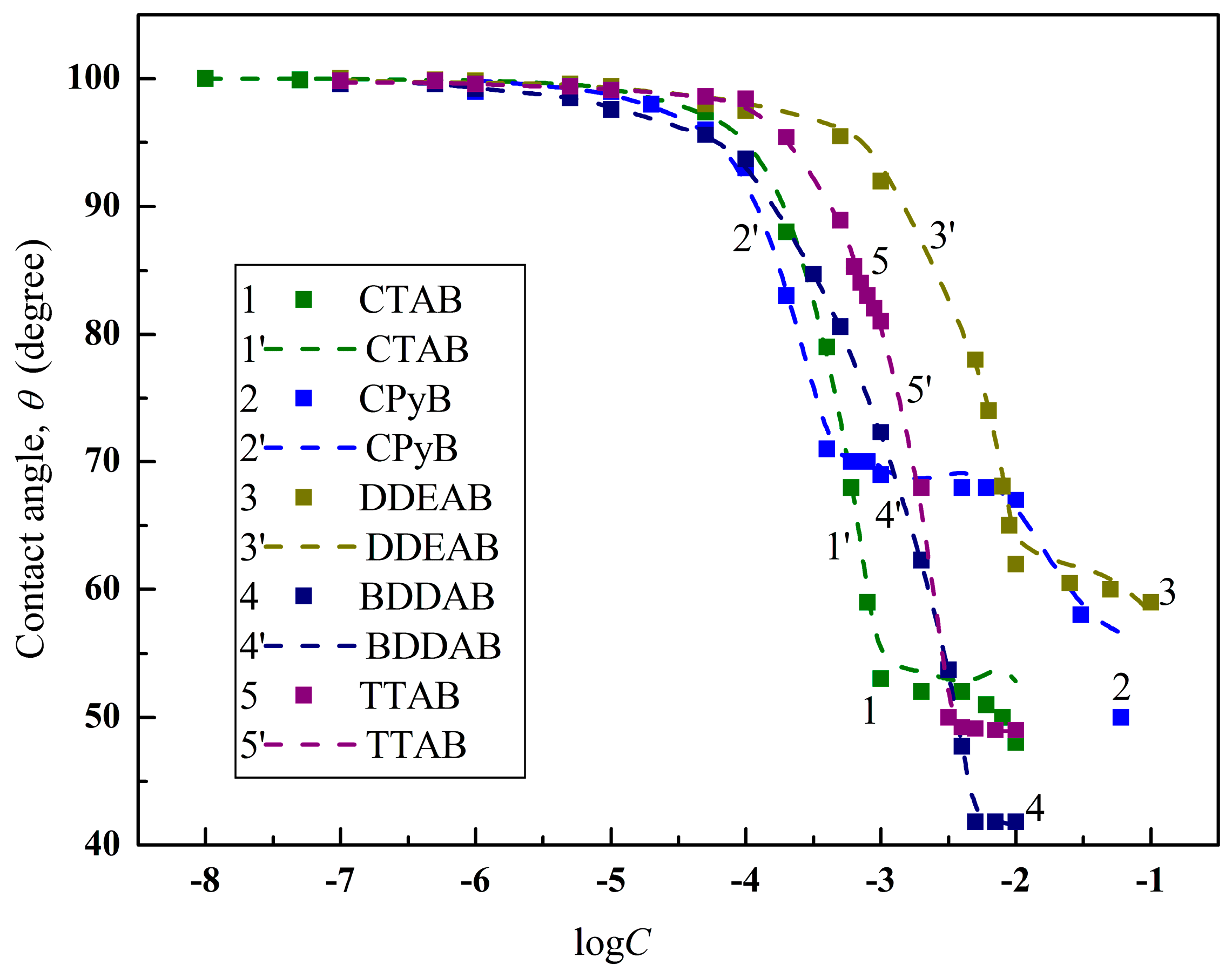
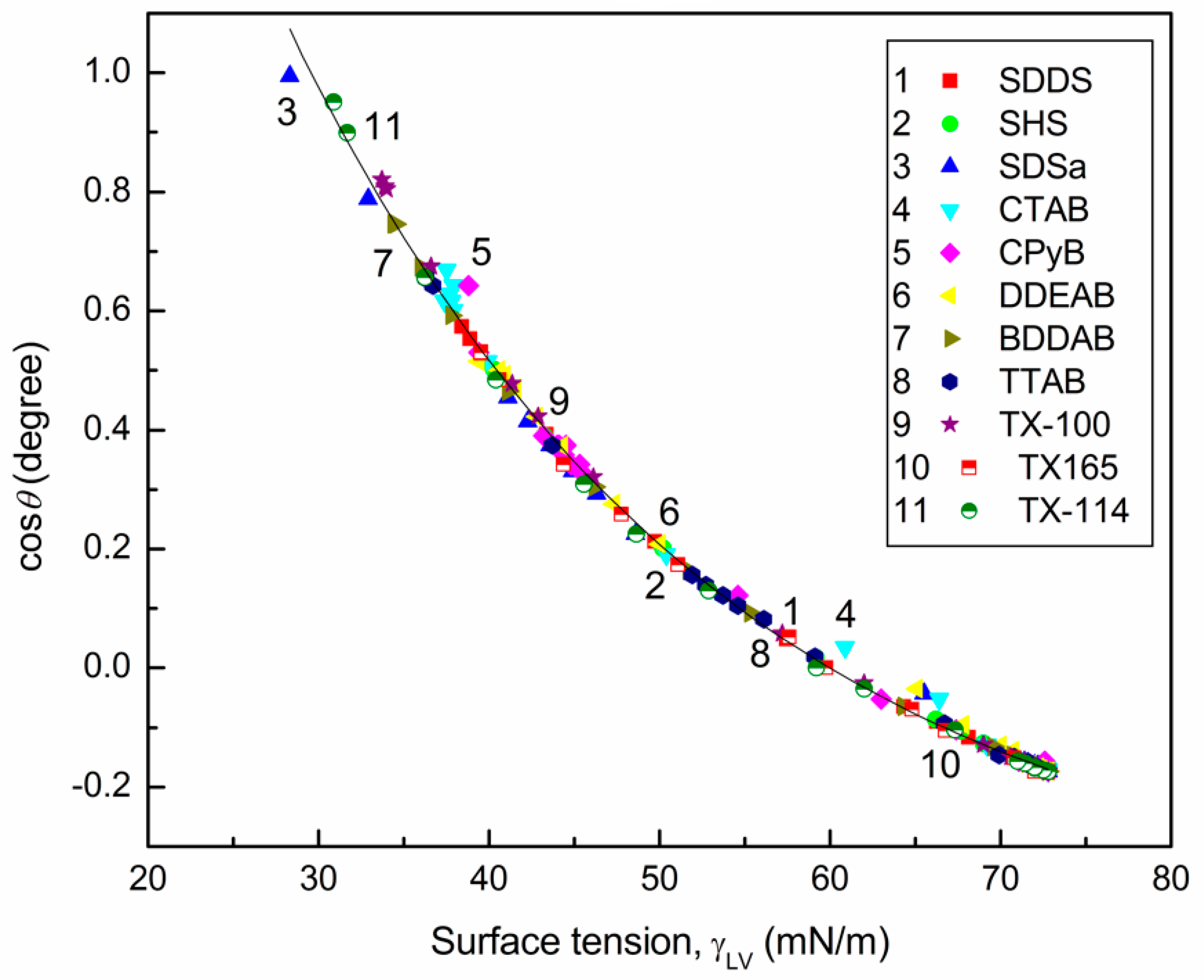
4.2. Prediction of the Contact Angles of Aqueous Solutions of Surface Active Agents on PTFE and PE Surfaces
4.3. Prediction of Adhesion Work of Surfactant Solutions to the Polymer Surface
5. Conclusions
Supplementary Materials
Author Contributions
Conflicts of Interest
References
- Tadros, T.F. Applied Surfactants: Principles and Applications; Wiley-VCH Verlag GmbH & Co., KGaA: Weinheim, Germany, 2005; pp. 85–113. [Google Scholar]
- Rosen, J.M. Surfactants and Interfacial Phenomena; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2004. [Google Scholar]
- Kumar Shah, S.; Bhattarai, A.; Kumar Chatterjee, S. Applications of Surfactants in Modern Science and Technology, Modern Trends in Science and Technology; Adhikari, D., Kumar Rai, S., Prassed Limbu, K., Eds.; National Nepal Biology Society, Nepal Physical Society (Easter Chapter): Kathmandu, Nepal, 2013; pp. 147–158. [Google Scholar]
- Adamson, A.W.; Gast, A.P. Physical Chemistry of Surfaces, 6th ed.; Wiley-Interscience: New York, NY, USA, 1997. [Google Scholar]
- Zisman, W.A. Contact Angle Wettability and Adhesion; Advances in Chemistry Series; American Chemical Society: Washington, DC, USA, 1964; Volume 43, pp. 1–51. [Google Scholar]
- Zisman, W.A. Contact Angle, Wettability and Adhesion. Adv. Chem. Ser. 1964, 43, 1–51. [Google Scholar]
- Bernett, M.K.; Zisman, W.A. Relation of wettability by aqueous solutions to the surface constitution of low-energy solids. J. Phys. Chem. 1959, 63, 1241–1246. [Google Scholar] [CrossRef]
- Bernett, M.K.; Zisman, W.A. Wetting of low-energy solids by aqueous solutions of highly fluorinated acid and salts. J. Phys. Chem. 1959, 63, 1911–1916. [Google Scholar] [CrossRef]
- Bargeman, D.; van Voorst Vader, F. Effect of surfactants on contact angles at nonpolar solids. J. Colloid Interface Sci. 1973, 42, 467–472. [Google Scholar] [CrossRef]
- Blake, T.D. Wetting. In Surfactants; Tadros, T.F., Ed.; Academic Press: London, UK, 1984. [Google Scholar]
- Zdziennicka, A.; Jańczuk, B.; Wójcik, W. The wettability of polytetrafluoroethylene by aqueous solutions of sodium dodecyl sulfate and propanol mixtures. J. Colloid Interface Sci. 2005, 281, 465–472. [Google Scholar] [CrossRef] [PubMed]
- Zdziennicka, A.; Jańczuk, B. The adsorption of cetyltrimethylammonium bromide and propanol mixtures with regard to wettability of polytetrafluoroethylene II. Adsorption at polytetrafluoroethylene–aqueous solution interface and wettability. J. Colloid Interface Sci. 2008, 318, 15–22. [Google Scholar] [CrossRef] [PubMed]
- Zdziennicka, A.; Jańczuk, B.; Wójcik, W. Wettability of polytetrafluoroethylene by aqueous solutions of two anionic surfactant mixtures. J. Colloid Interface Sci. 2003, 268, 200–207. [Google Scholar] [CrossRef]
- Szymczyk, K.; Zdziennicka, A.; Jańczuk, B.; Wójcik, W. The wettability of polytetrafluoroethylene and polymethyl methacrylate by aqueous solution of two cationic surfactants mixture. J. Colloid Interface Sci. 2006, 293, 172–180. [Google Scholar] [CrossRef] [PubMed]
- Szymczyk, K.; Jańczuk, B. The wettability of polytetrafluoroethylene by aqueous solution of cetyltrimethylammonium bromide and Triton X-100 mixture. J. Colloid Interface Sci. 2006, 303, 319–325. [Google Scholar] [CrossRef] [PubMed]
- Krawczyk, J.; Szymczyk, K.; Zdziennicka, A.; Jańczuk, B. Wettability of polymers by aqueous solution of binary surfactants mixture with regard to adhesion in polymer–solution system II. Critical surface tension of polymers wetting and work of adhesion. Int. J. Adhes. Ades. 2013, 45, 106–111. [Google Scholar] [CrossRef]
- Szymczyk, K.; Jańczuk, B. The wettability of poly(tetrafluoroethylene) by aqueous solutions of ternary surfactant mixtures. Appl. Surface Sci. 2010, 256, 478–483. [Google Scholar] [CrossRef]
- Szymczyk, K.; Zdziennicka, A.; Krawczyk, J.; Jańczuk, B. Wettability, adhesion, adsorption and interface tension in the polymer/surfactant aqueous solution system. I. Critical surface tension of polymer wetting and its surface tension. Colloids Surf. A 2012, 402, 132–138. [Google Scholar] [CrossRef]
- Szymczyk, K.; Jańczuk, B. Wettability of a polytetrafluoroethylene surface by an aqueous solution of two nonionic surfactant mixtures. Langmuir 2007, 23, 8740–8746. [Google Scholar] [CrossRef] [PubMed]
- Gray, V.R. Contact angles of mercury on low-energy solids. Nature 1966, 209, 608–609. [Google Scholar] [CrossRef]
- Rhee, S.K. A method for determining surface energy of solids. Mater. Sci. Eng. 1973, 11, 311–318. [Google Scholar] [CrossRef]
- Girifalco, F.A.; Good, R.J. A theory for the estimation of surface and interfacial energies. I. Derivation and application to interfacial tension. J. Phys. Chem. 1957, 61, 904–909. [Google Scholar] [CrossRef]
- Spelt, J.K.; Li, D.; Neumann, A.W. The equation of state approach to interfacial tensions. In Modern Approaches to Wettability; Schrader, M.E., Loeb, G.L., Eds.; Plenum Press: New York, NY, USA, 1992. [Google Scholar]
- Li, D.; Neumann, A.W. Equation of state for interfacial tensions of solid-liquid systems. Adv. Colloid Interface Sci. 1992, 39, 299–345. [Google Scholar] [CrossRef]
- Kwok, D.Y.; Neumann, A.W. Contact angle measurement and contact angle interpretation. Adv. Colloid Interface Sci. 1999, 81, 167–249. [Google Scholar] [CrossRef]
- Kwok, D.Y.; Neumann, A.W. Contact angle interpretation in terms of solid surface tension. Colloids Surf. A 2000, 161, 31–48. [Google Scholar] [CrossRef]
- Van Oss, C.J. Interfacial Forces in Aqueous Media; Marcel Dekker: New York, NY, USA, 1994. [Google Scholar]
- Van Oss, C.J.; Good, R.J. Surface tension and the solubility of polymers and biopolymers: The role of polar and apolar interfacial free energies. J. Macromol. Sci. 1989, 26, 1183–1203. [Google Scholar] [CrossRef]
- Van Oss, C.J.; Chaudhury, M.K.; Good, R.J. Monopolar surfaces. Adv. Colloid Interface Sci. 1987, 28, 35–64. [Google Scholar] [CrossRef]
- Van Oss, C.J.; Good, R.J.; Chaudhury, M.K. Additive and nonadditive surface tension components and the interpretation of contact angles. Langmuir 1988, 4, 884–891. [Google Scholar] [CrossRef]
- Van Oss, C.J.; Good, R.J. The modern theory of contact angles and the hydrogen bond components of surface energies. In Theory and Applications; Schrader, M.E., Loeb, G., Eds.; Plenum Press: New York, NY, USA, 1991. [Google Scholar]
- Zdziennicka, A.; Krawczyk, J.; Szymczyk, K.; Jańczuk, B. Components and parameters of liquids and some polymers surface tension at different temperature. Colloids Surf. A 2017, 529, 864–875. [Google Scholar] [CrossRef]
- Schrader, M.E. Spreading preassure in the Young equation and intermolecular force theory. Langmuir 1993, 9, 1959–1961. [Google Scholar] [CrossRef]
- Lucassen-Reynders, E.H. Contact angles and adsorption on solids. J. Phys. Chem. 1963, 67, 969–972. [Google Scholar] [CrossRef]
- Tsubone, K.; Rosen, M.J. Structural effect on surface activities of anionic surfactants having N-acyl-N-methylamide and carboxylate groups. J. Colloid Interface Sci. 2001, 244, 394–398. [Google Scholar] [CrossRef]
- Fowkes, F.M. Attractive forces at interfaces. Ind. Eng. Chem. 1964, 56, 40–52. [Google Scholar] [CrossRef]
- Bielawska, M.; Zdziennicka, A.; Jańczuk, B. Correlation between adhesion of aqueous solutions of nonionic and anionic surfactant mixture with short-chain alcohols to polymer surface and their adsorption at interfaces. II. Critical surface tension of polymer wetting and work of adhesion. Int. J. Adhes. Adhes. 2017, 74, 194–199. [Google Scholar] [CrossRef]



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zdziennicka, A.; Krawczyk, J.; Jańczuk, B. Wettability and Adhesion Work Prediction in the Polymer–Aqueous Solution of Surface Active Agent Systems. Colloids Interfaces 2018, 2, 21. https://doi.org/10.3390/colloids2020021
Zdziennicka A, Krawczyk J, Jańczuk B. Wettability and Adhesion Work Prediction in the Polymer–Aqueous Solution of Surface Active Agent Systems. Colloids and Interfaces. 2018; 2(2):21. https://doi.org/10.3390/colloids2020021
Chicago/Turabian StyleZdziennicka, Anna, Joanna Krawczyk, and Bronisław Jańczuk. 2018. "Wettability and Adhesion Work Prediction in the Polymer–Aqueous Solution of Surface Active Agent Systems" Colloids and Interfaces 2, no. 2: 21. https://doi.org/10.3390/colloids2020021