Flexural Characteristics of Functionally Layered Fiber-Reinforced Cementitious Composite with Polyvinyl Alcohol Fibers
Abstract
:1. Introduction
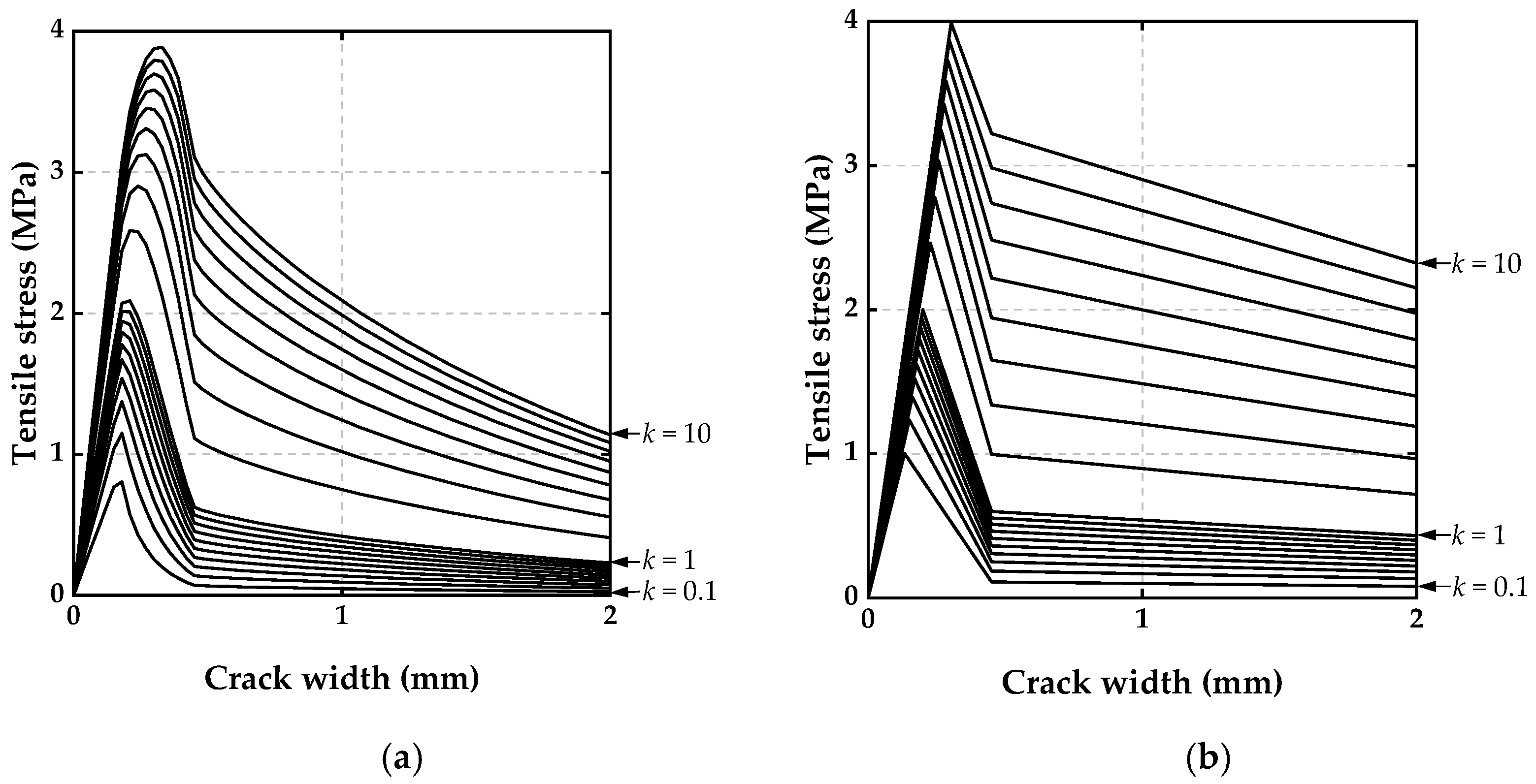
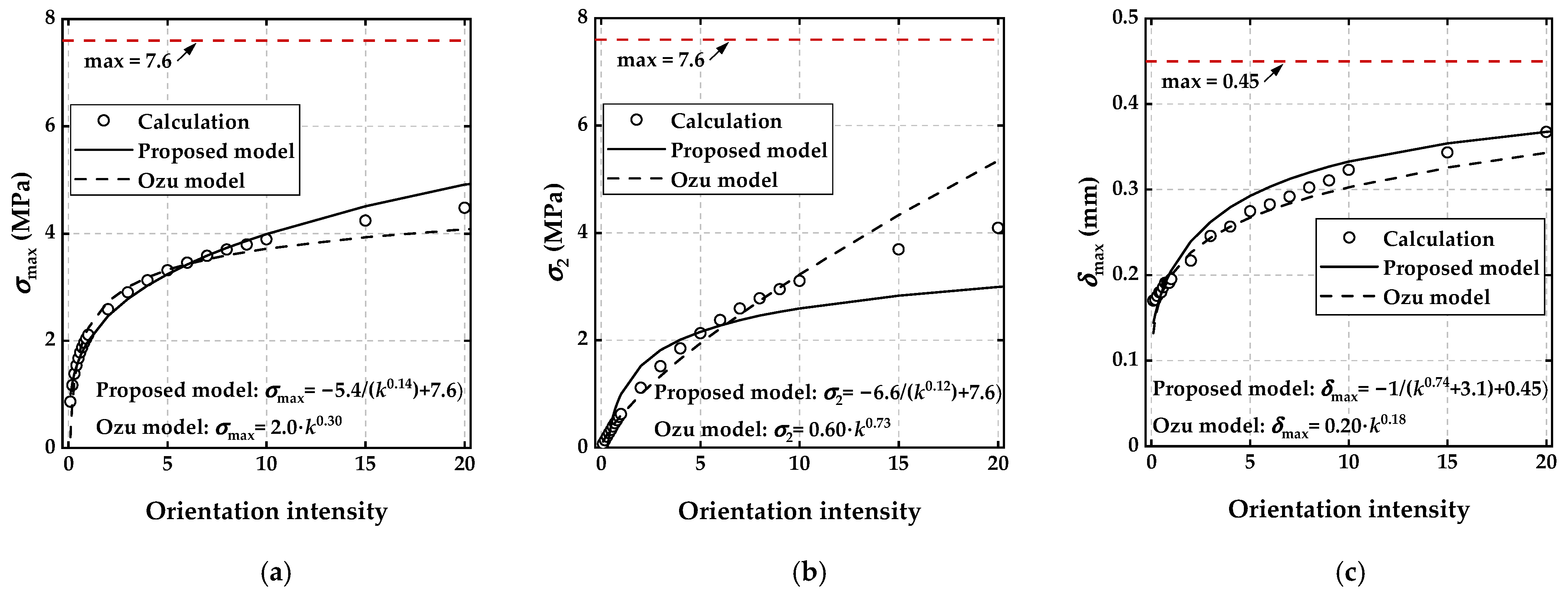
2. Modification of the Bridging Law for PVA-FRCC
3. Experiment Program
3.1. Materials
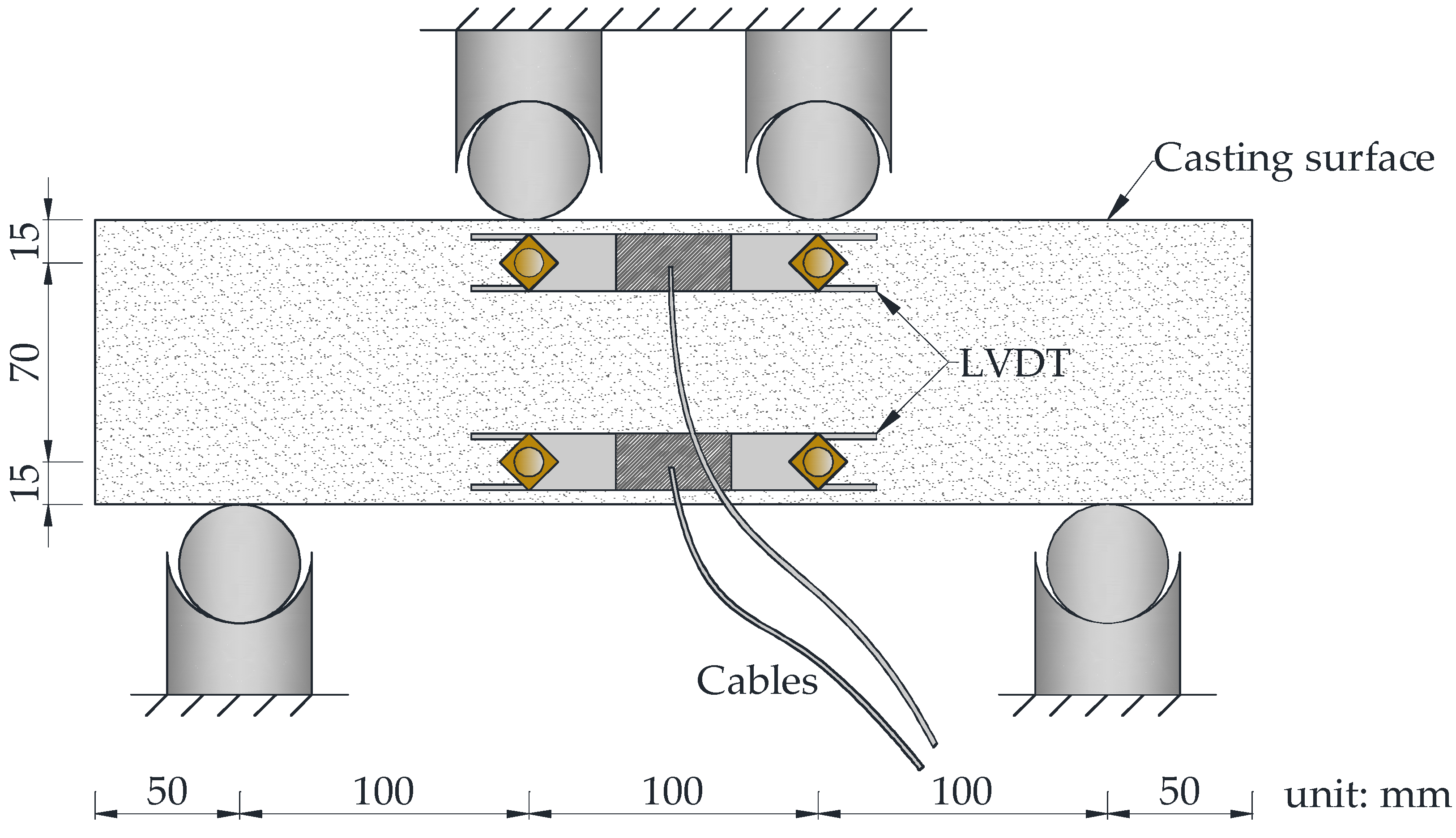
3.2. Specimen
4. Experiment Results
4.1. Failure Pattern
4.2. Bending Moment: A Curvature Relationship
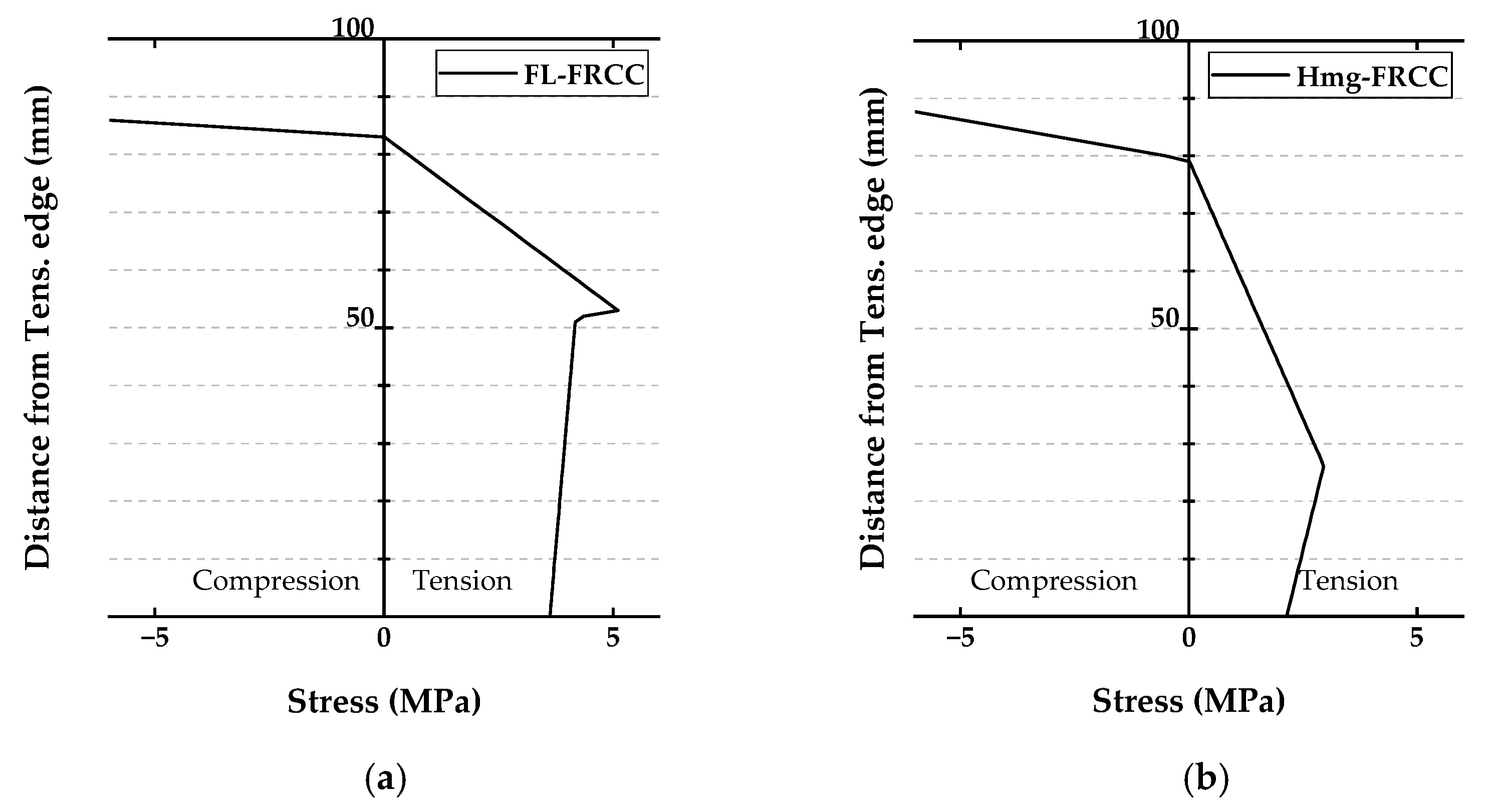
4.3. Comparison of the Section Analysis and Experiment Results
5. Conclusions
- Based on the previous visualization simulation results, a bridging law model is proposed with a wider range of fiber orientation intensity applications, including the situation of being infinite. Compared to the Ozu model, the proposed model has proven to have a better fitting and predicting effect;
- FL-FRCC specimens, in which the thickness of each layer is smaller than the fiber length and the mixed fibers tend to show a 2-D orientation, are fabricated. Bending tests were conducted and the results show that the average maximum bending moment of FL-FRCC specimens is nearly twice that of the Hmg-FRCC specimens. The bending moment-curvature curves of FL-FRCC specimens shows a steeper decline phase after reaching the maximum bending moment compared to that of Hmg-FRCC specimens. And the absorbed energy of FL-FRCC specimens is also larger than that of Hmg-FRCC specimens. These facts suggest the FL-FRCC specimens can lead to a larger bending capacity and also the relative brittleness compared to the Hmg-FRCC specimens;
- Section analysis based on the proposed stress–strain model was conducted. The ratio of the experiment to analysis ranged from 0.93 to 0.98, which can lead to the conclusion that the section analysis shows a good adaptability with the experiment result. Curvatures at the maximum bending moment calculated by the section analysis do not show good adaptability with the ones obtained by the experiment. The reasons for that are considered to be that the layered FRCC would cause a chain of fractures in each adjacent layer in the case of FL-FRCC specimens. In the case of Hmg-FRCC specimens, the wide constant moment region around the maximum bending moment leads to the scattering of the curvature at the maximum;
- For FL-FRCC specimens, the tensile stress reaches the maximum at approximately half of the cross-section height from the compression edge; it is considered that FL-FRCC specimens can effectively apply the bending capacity of the whole specimen compared to the Hmg-FRCC specimens.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, V.C. Engineered Cementitious Composites (ECC)—Bendable Concrete for Sustainable and Resilient Infrastructure; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Rokugo, K.; Kanda, T. Strain Hardening Cement Composites: Structural Design and Performance; RILEM State-of-the-Art Reports 6; E. & FN Spon: London, UK, 2013. [Google Scholar]
- Li, V.C. On Engineered Cementitious Composites (ECC)—A Review of the Material and Its Applications. J. Adv. Concr. Technol. 2003, 1, 215–230. [Google Scholar] [CrossRef] [Green Version]
- Li, V.C. Progress and Application of Engineered Cementitious Composites. J. Chin. Ceram. Soc. 2007, 35, 531–536. [Google Scholar]
- Balaguru, P.N.; Shah, S.P. Introduction, Fiber-Reinforced Cement Composites; McGraw-Hill: New York, NY, USA, 1992; pp. 1–15. [Google Scholar]
- Zollo, R.F. Collated Fibrillated Polypropylene Fibers in FRC. In Proceedings of the Fiber Reinforced Concrete International Symposium (ACI SP-81), Detroit, MI, USA, 1 November 1984; pp. 397–409. [Google Scholar]
- Naaman, A.E.; Reinhardt, H.W. High Performance Fiber Reinforced Cement Composites: HPFRCC 2; E. & FN Spon: London, UK, 1996. [Google Scholar]
- Li, V.C. Large volume, high-performance applications of fibers in civil engineering. J. Appl. Polym. Sci. 2002, 83, 660–686. [Google Scholar] [CrossRef] [Green Version]
- Laranjeira, F.; Aguado, A.; Molins, C.; Grünewald, S.; Walraven, J.; Cavalaro, S. Framework to predict the orientation of fibers in FRC: A novel philosophy. Cem. Concr. Res. 2012, 42, 752–768. [Google Scholar] [CrossRef]
- Krenchel, H. Fibre Spacing and Specific Fibre Surface. Fibre Reinf. Cem. Concr. 1975, 1975, 69–79. [Google Scholar]
- Laranjeira, F. Design Oriented Constitutive Model for Steel Fiber Reinforced Concrete. Ph.D. Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 26 March 2010. [Google Scholar]
- Li, V.C.; Wang, S. On High Performance Fiber Reinforced Cementitious Composites. In Proceedings of the JCI Symposium on Ductile Fiber-Reinforced Cementitious Composites, Tokyo, Japan, 4–5 December 2003; pp. 13–23. [Google Scholar]
- Kanakubo, T.; Miyaguchi, M.; Asano, K. Influence of Fiber Orientation on Bridging Performance of Polyvinyl Alcohol Fiber-Reinforced Cementitious Composite. ACI Mater. J. 2016, 113, 131–141. [Google Scholar] [CrossRef]
- Duque, L.F.M.; Grayeal, B. Fiber orientation distribution and tensile mechanical response in UHPFRC. Mater Struct. 2017, 50, 55. [Google Scholar] [CrossRef]
- Kang, S.T.; Kim, J.K. Investigation on the flexural behavior of UHPCC considering the effect of fiber orientation distribution. Const. Bldg. Mater. 2012, 28, 57–65. [Google Scholar] [CrossRef]
- Gupta, A.; Talha, M. Recent development in modeling and analysis of functionally graded materials and structures. Prog. Aerosp. Sci. 2015, 79, 1–14. [Google Scholar] [CrossRef]
- Pompe, W.; Worch, H.; Epple, M. Functionally Graded Materials for Biomedical Applications. Mater. Sci. Eng. A 2003, 362, 40–60. [Google Scholar] [CrossRef]
- El-Galy, I.M.; Saleh, B.I.; Ahmed, M.H. Functionally Graded Materials Classifications and Development Trends from Industrial Point of View. SN Appl. Sci. 2019, 1, 1378. [Google Scholar] [CrossRef] [Green Version]
- Zhou, F.; Zhou, R.; Du, Y.; Wang, Y. Flexural Behavior of Layered CTRC-ECC Reinforced Cementitious Composite Plates. J. Bldg. Eng. 2022, 62, 105283. [Google Scholar] [CrossRef]
- Yuan, H.; Fu, X.H.; Fan, Y.C.; Fu, B.; Zou, Q.Q. Flexural Performance of Layered Macro Fiber Reinforced Concrete Beams. Const. Bldg. Mater. 2022, 357, 129314. [Google Scholar] [CrossRef]
- Rydval, M.; Čítek, D.; Kolísko, J.; Nenadálová, Š.; Bittner, T. Functionally Layered Thin Slabs Made from UHPC and ECC Composites. Solid State Phenom. 2017, 259, 90–96. [Google Scholar] [CrossRef]
- Akshaya, S.L.; Prakash, A.; Bharati Raj, J. Applications of Functionally Graded Materials in Structural Engineering—A Review. In Proceedings of SECON 2020; Lecture Notes in Civil Engineering; Springer: Berlin/Heidelberg, Germany, 2020; Volume 97. [Google Scholar]
- Liu, Q.; Zhang, H.; Hong, P.; Han, S. A Brief Review on the Fabrication and Mechanical Behavior of Functionally Graded Concrete Materials. IOP Conf. Ser. Earth Environ. Sci. 2020, 525, 012142. [Google Scholar] [CrossRef]
- Torelli, G.; Lees, J.M. Interface bond strength of lightweight low-cement functionally layered concrete elements. Const. Bldg. Mater. 2020, 249, 118614. [Google Scholar] [CrossRef]
- Dias, C.; Savastano, H.; John, V.M. Exploring the potential of functionally graded materials concept for the development of fiber cement. Const. Bldg. Mater. 2010, 24, 140–146. [Google Scholar] [CrossRef]
- Lai, J.; Zhou, J.; Yin, X.; Zheng, X. Dynamic behavior of functional graded cementitious composite under the coupling of high speed penetration and explosion. Compos. Struct. 2021, 274, 114326. [Google Scholar] [CrossRef]
- Bao, S.; Zhang, Y.; Liu, H.; Zeng, K.; Zhang, W. Optimization design of functionally graded ultra-high performance cementitious composite on flexural behavior. Struct. Concr. 2023, 24, 2245–2259. [Google Scholar] [CrossRef]
- Kanakubo, T.; Koba, T. Flexural characteristics of functionally graded fiber-reinforced cementitious composite with polyvinyl alcohol fiber. J. Compos. Sci. 2021, 5, 94. [Google Scholar] [CrossRef]
- Zhang, H.; Kanakubo, T. Influence of Placing Thickness on Fiber Orientation and Bridging Law of FRCC. In Strain Hardening Cementitious Composites; SHCC 2022; RILEM Bookseries; Springer: Berlin/Heidelberg, Germany, 2022; Volume 39. [Google Scholar]
- Ozu, Y.; Miyaguchi, M.; Kanakubo, T. Modeling of Bridging Law for PVA Fiber-Reinforced Cementitious Composite Considering Fiber Orientation. J. Civ. Eng. Archit. 2018, 12, 651–661. [Google Scholar]
- JSCE-F 531-2013; Standard Specifications for Concrete Structures — 2013, Test Methods and Specifications. Japan Society of Civil Engineers: Tokyo, Japan, 2013; pp. 281–282. (In Japanese)
- JIS K 5400; Testing Methods for Paints. Japanese Industrial Standard. Japanese Standards Association (JSA): Tokyo, Japan, 1990. (In Japanese)
- ISO 21914: 2019; Test Methods for Fibre-Reinforced Cementitious Composites—Bending Moment—Curvature Curve by Four-Point Bending Test. ISO: Geneva, Switzerland, 2019.
- ISO 1920-4: 2020; Testing of Concrete—Part 4: Strength of Hardened Concrete. ISO: Geneva, Switzerland, 2020.
- Popovics, S. A numerical approach to the complete stress-strain curve of concrete. Cem. Concr. Res. 1973, 3, 583–599. [Google Scholar] [CrossRef]










| Type | Diameter (mm) | Length (mm) | Tensile Strength (MPa) | Elastic Modulus (GPa) |
|---|---|---|---|---|
| PVA | 0.10 | 12 | 1200 | 28 |
| Water to Binder Ratio | Sand by Binder Ratio | Unit Weight (kg/m3) | ||||
|---|---|---|---|---|---|---|
| Water | Cement | Fly Ash | Sand | PVA Fiber | ||
| 0.39 | 0.50 | 380 | 678 | 291 | 484 | 26 |
| Specimen Type | Dimensions L × W × H (mm) | Number of Specimens |
|---|---|---|
| FL-FRCC | 400 × 100 × 10 × 9 layers | 3 |
| Hmg-FRCC | 400 × 100 × 100 | 5 |
| Specific Gravity (Hardened Product) | Viscosity | Concrete Adhesive Strength * (N/mm2) | |
|---|---|---|---|
| Test value | 1.92 | Putty-liked | 3.2 |
| Specimen No. | Height at Measuring Point (mm) | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | Average | |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 | ||
| 1 | 103.2 | 100.8 | 99.2 | 97.8 | 105.1 | 101.6 | 101.7 | 100.9 |
| 99.1 | 97.1 | 98.0 | 99.2 | 104.2 | 103.1 | 103.0 | ||
| 2 | 100.4 | 100.7 | 100.8 | 99.7 | 100.2 | 99.7 | 101.7 | 100.0 |
| 99.6 | 98.8 | 99.0 | 99.0 | 100.0 | 100.0 | 100.0 | ||
| 3 | 101.8 | 101.8 | 101.6 | 101.3 | 101.4 | 101.6 | 101.8 | 101.8 |
| 102.6 | 102.4 | 102.3 | 102.6 | 102.0 | 101.8 | 100.5 | ||
| Experiment | Section Analysis | ||||||
|---|---|---|---|---|---|---|---|
| Specimen Type | Max. Bending Moment | Curvature at | Absorbed Energy (N·m) | Max Bending Moment | Curvature at | Ratio of Experiment to Analysis | |
| Avg. | STDV | Avg. | Avg. | ||||
| FL-FRCC | 1.62 | 0.176 | 0.022 | 47.3 | 1.66 | 0.136 | 0.98 |
| Hmg-FRCC | 0.87 | 0.036 | 0.119 | 41.6 | 0.94 | 0.048 | 0.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Kanakubo, T. Flexural Characteristics of Functionally Layered Fiber-Reinforced Cementitious Composite with Polyvinyl Alcohol Fibers. J. Compos. Sci. 2023, 7, 293. https://doi.org/10.3390/jcs7070293
Zhang H, Kanakubo T. Flexural Characteristics of Functionally Layered Fiber-Reinforced Cementitious Composite with Polyvinyl Alcohol Fibers. Journal of Composites Science. 2023; 7(7):293. https://doi.org/10.3390/jcs7070293
Chicago/Turabian StyleZhang, Hang, and Toshiyuki Kanakubo. 2023. "Flexural Characteristics of Functionally Layered Fiber-Reinforced Cementitious Composite with Polyvinyl Alcohol Fibers" Journal of Composites Science 7, no. 7: 293. https://doi.org/10.3390/jcs7070293






