Influence on the Flexural Behaviour of High-Volume Fly-Ash-Based Concrete Slab Reinforced with Sustainable Glass-Fibre-Reinforced Polymer Sheets
Abstract
:1. Introduction
2. Materials and Methods
2.1. Ingredients of OPC/HVFA Concrete
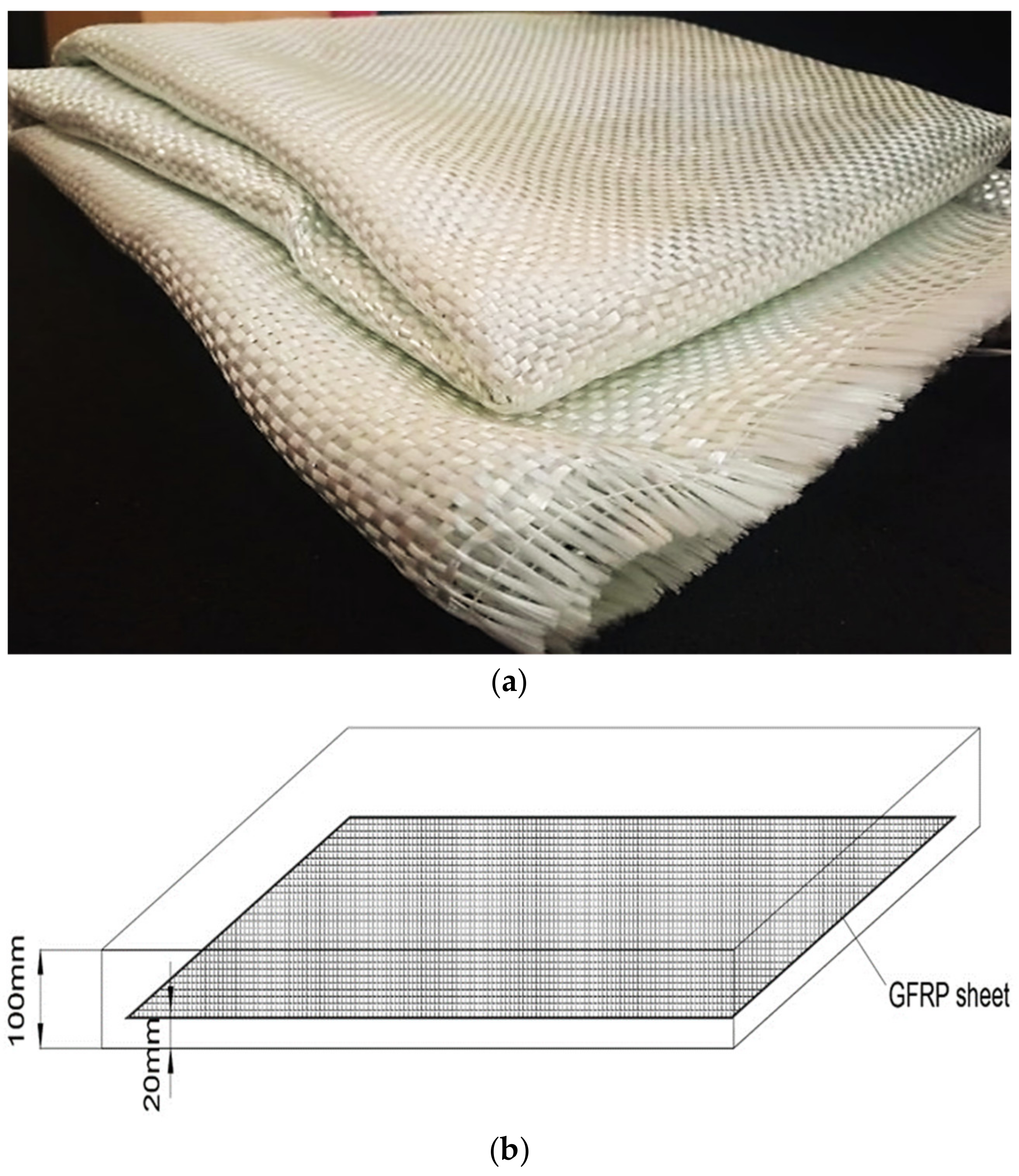
2.2. Reinforcing System
3. Experimental Investigation
3.1. Specimen Geometry and Detailing
3.2. Experimental Set-Up
4. Results and Discussion
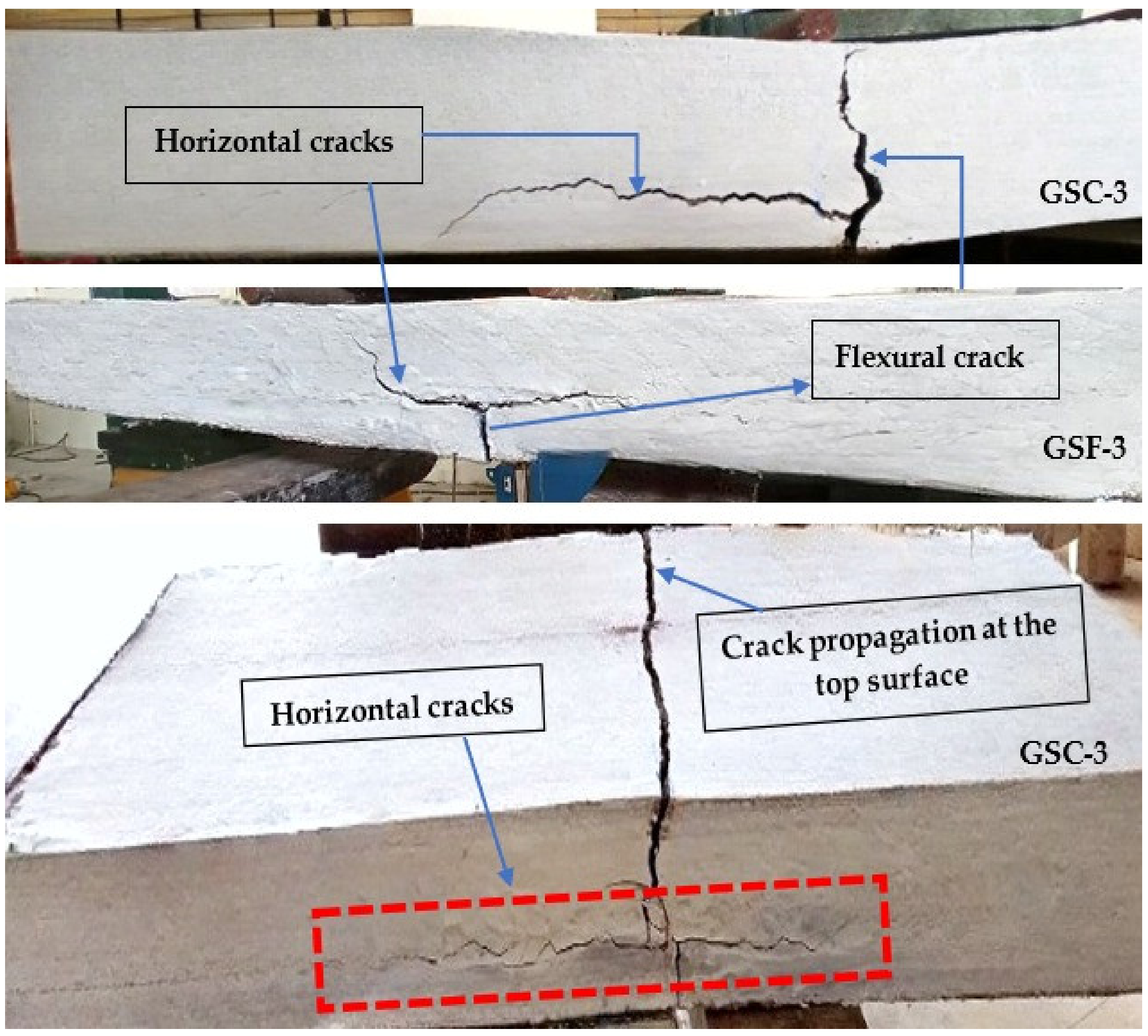
4.1. Cracking Behaviour
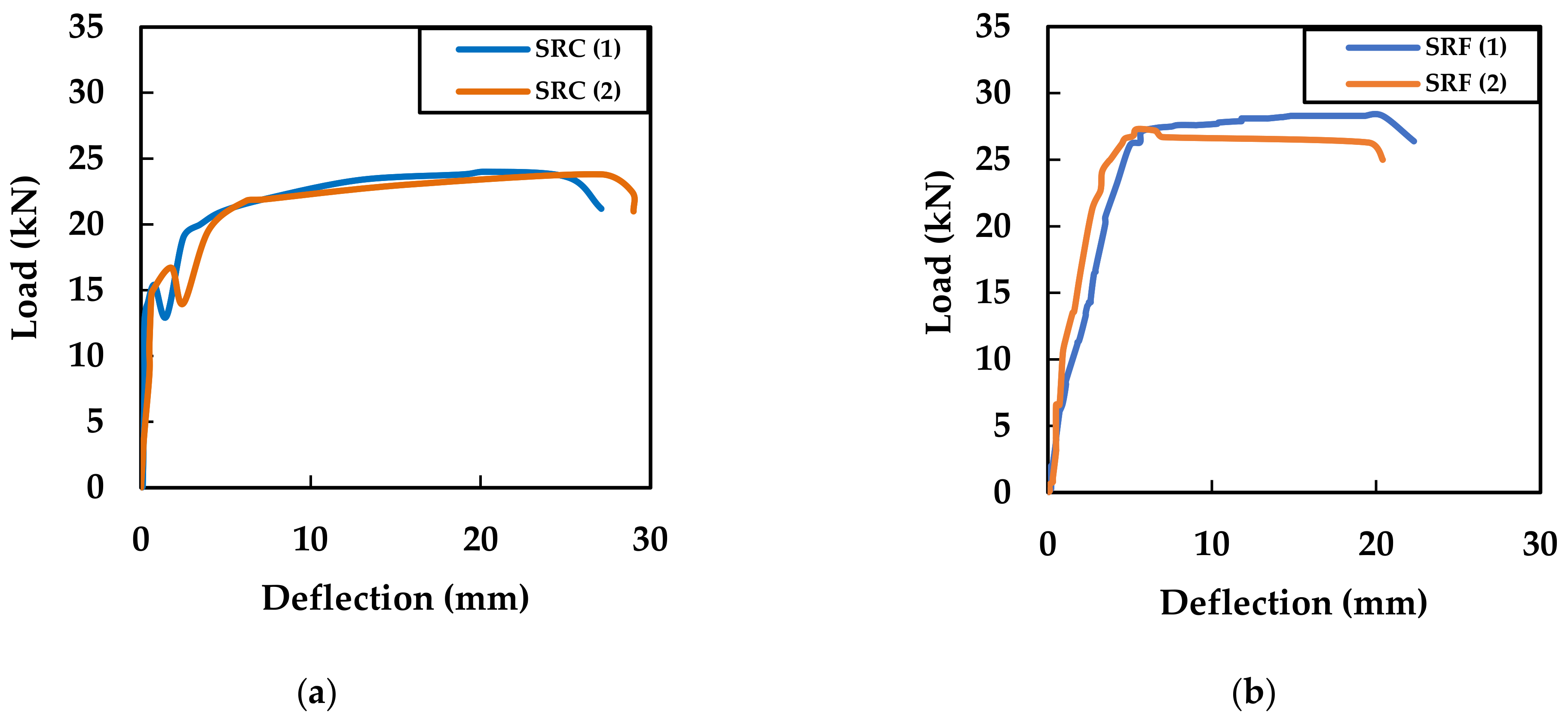
4.2. Load–Deflection Behaviour
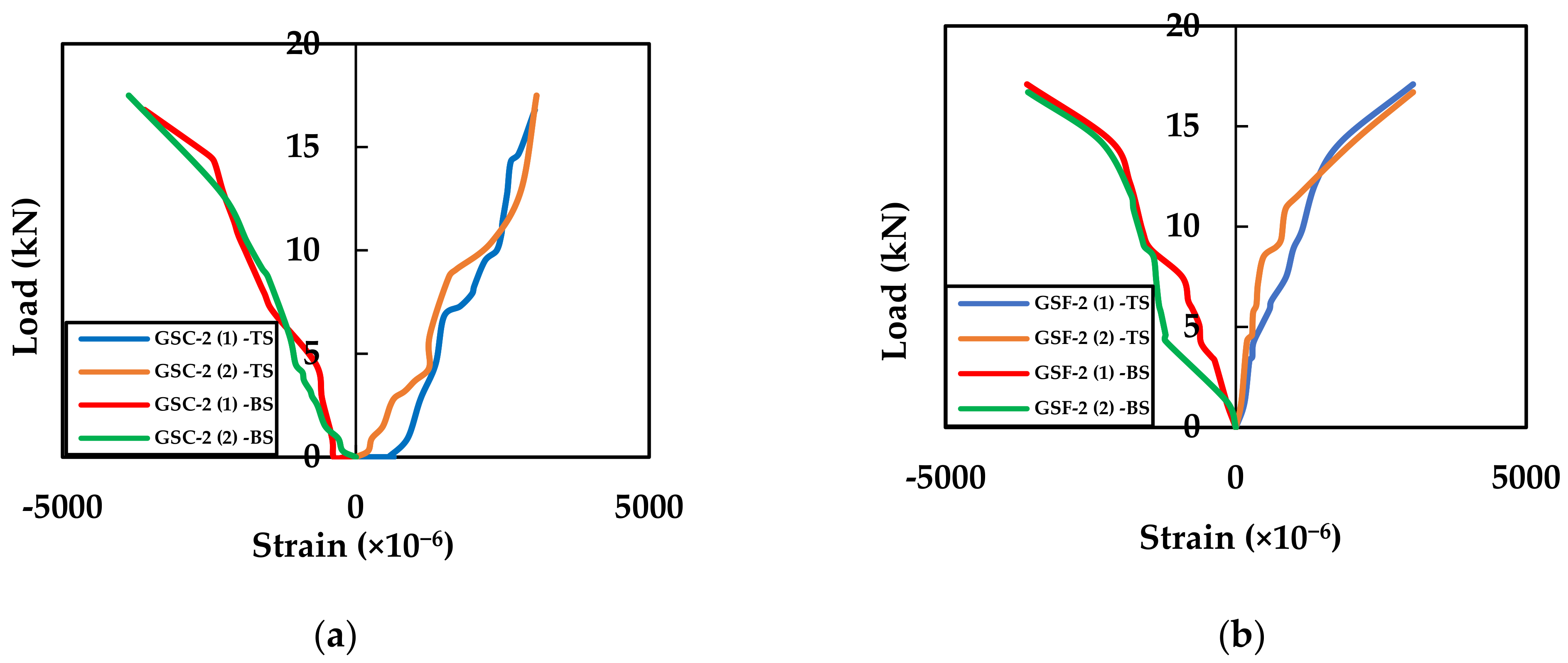
4.3. Strain Distribution
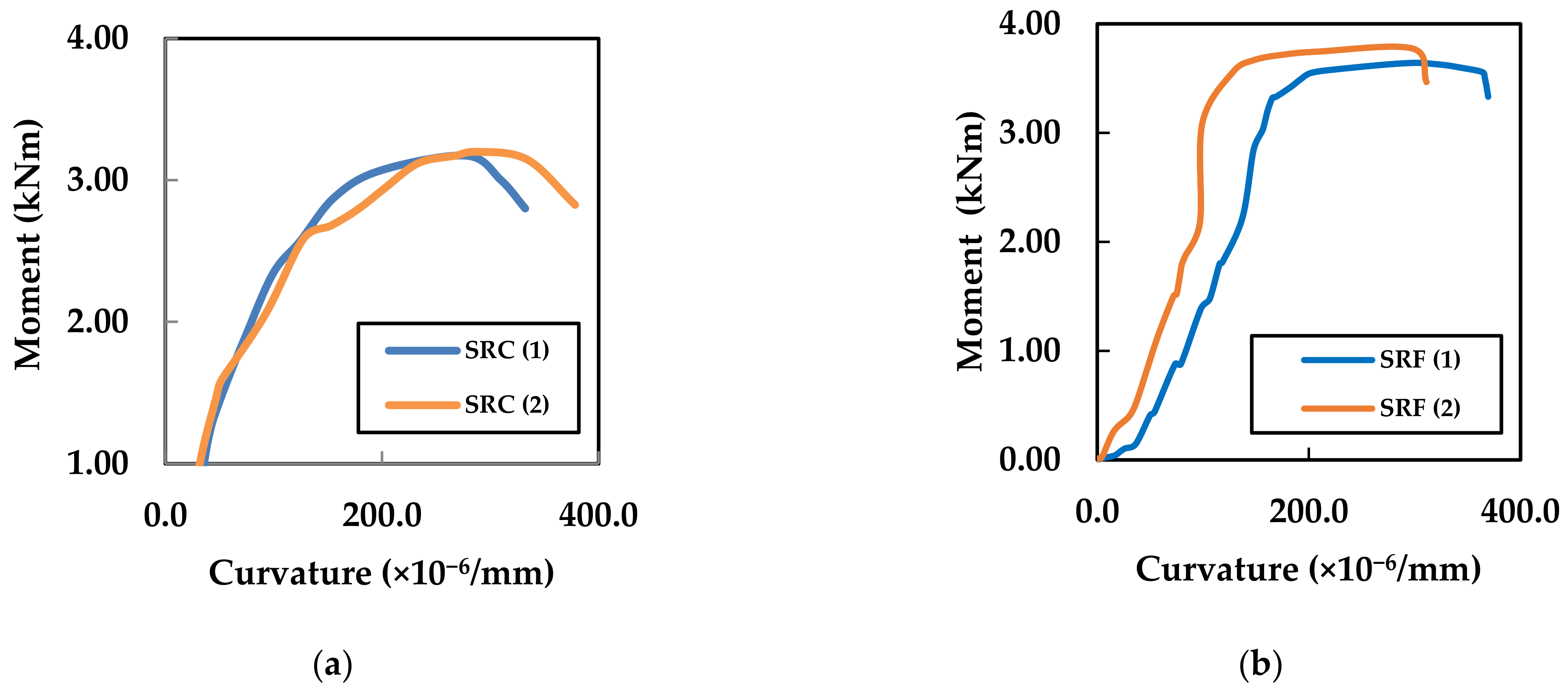
4.4. Moment–Curvature
5. Numerical Analysis and Consecutive Models
5.1. Considerations for Element Types
5.2. Modelling and Numerical Solution
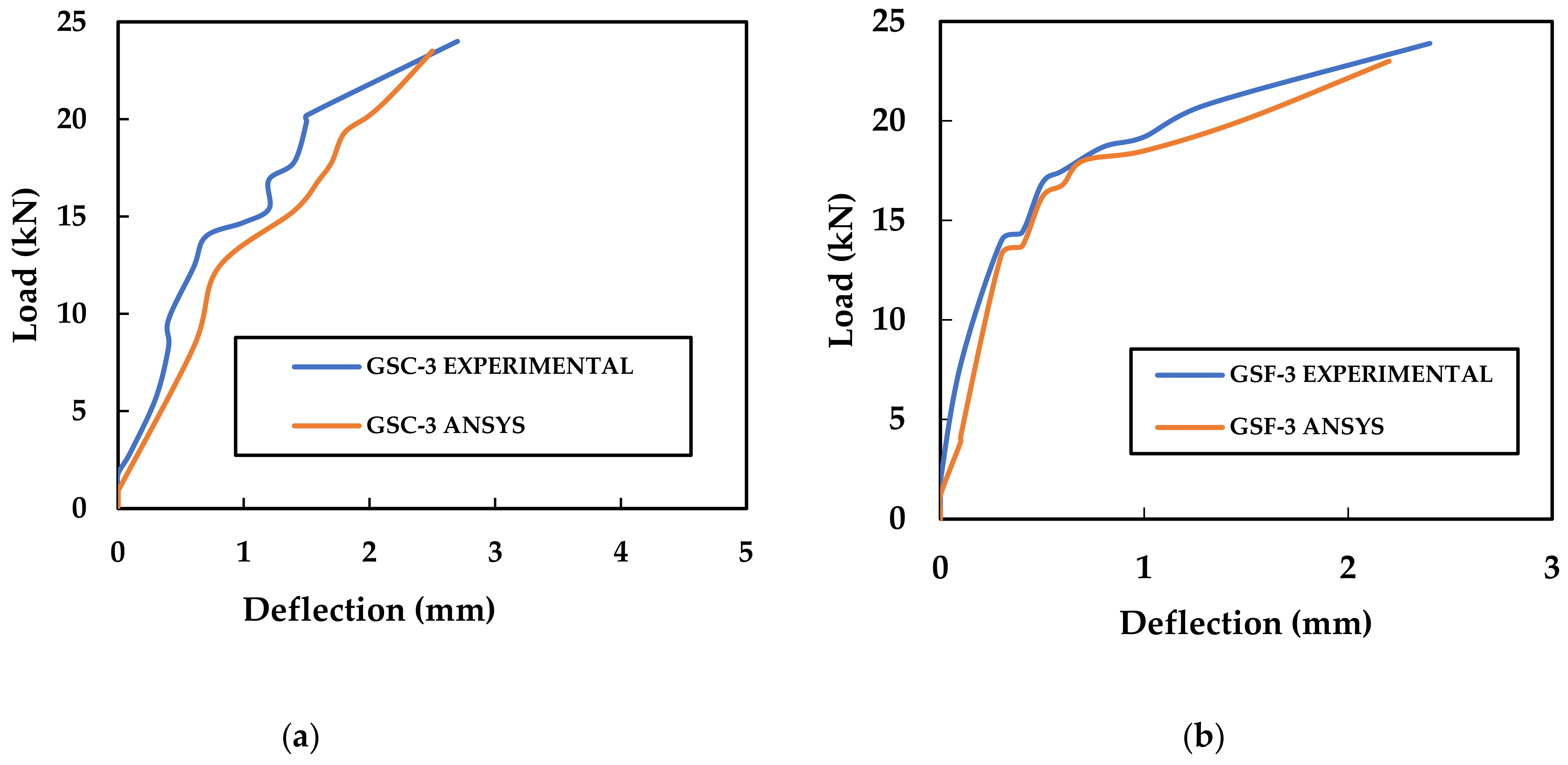
5.3. Comparison of Experimental Results with NLFEA Results
6. Conclusions
- HVFA slabs reinforced with the steel bars (SRF) recorded a 17% increase in their ultimate load-carrying capacity compared with the OPC slabs reinforced with the steel bars (SRC).
- All the specimens failed due to the formation of flexural cracks that propagate to the top surface at failure with concrete crushing. Slabs reinforced with two layers of GFRP sheets failed in the formation of flexural cracks under the two-loading point. However, the slab reinforced with three layers and four layers of GFRP sheets showed flexural cracks as well as horizontal cracks.
- The average ultimate load-carrying capacity of OPC/HVFA concrete slabs reinforced with three layers of GFRP sheets (GSC-3/GSF-3) has the same strength as that of slabs reinforced with the steel bars (SRC).
- The ultimate average load-carrying capacity of a slab reinforced with three layers of GFRP sheets (GSC-3 and GSF-3) is more than that of the slabs reinforced with two and four layers (GSC-2, GSC-4, GSF-2 and GSF-4) by 39%, 49%, 41% and 53%, respectively.
- Less than 10% difference in the ultimate load and ultimate deflection of SRC, SRF, GSC-3 and GSF-3 was observed between the experimental and NLFEM results. Hence, ANSYS Workbench 2022-R1 software could be used for the numerical analysis of fly-ash concrete slabs reinforced with a GFRP sheet.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ji, H.; Son, B.; Ma, Z. Evaluation of Composite Sandwich Bridge Decks with Hybrid FRP-Steel Core. J. Bridg. Eng. 2009, 14, 36–44. [Google Scholar] [CrossRef]
- Shin, Y.S.; Lee, C. Flexural behaviour of reinforced concrete beams strengthened with carbon fibre-reinforced polymer laminates at different levels of sustaining load. ACI Struct. J. 2003, 100, 231–239. [Google Scholar]
- Teng, J.G.; Chen, J.F.; Smith, S.T.; Lam, L. Behaviour and strength of FRP-strengthened RC structures: A state-of-the-art review. Proc. Inst. Civ. Eng.-Struct. Build. 2003, 156, 51–62. [Google Scholar] [CrossRef]
- Djamaluddin, R.; Irmawaty, R.; Tata, A. Flexural Capacity of Reinforced Concrete Beams Strengthened Using GFRP Sheet after Fatigue Loading for Sustainable Construction. Key Eng. Mater. 2016, 692, 66–73. [Google Scholar] [CrossRef]
- Sethi, A.K.; Kinjawadekar, T.A.; Nagarajan, P.; Shashikala, A.P. Design of Flexural Members Reinforced with GFRP Bars. IOP Conf. Ser. Mater. Sci. Eng. 2020, 936, 012036. [Google Scholar] [CrossRef]
- Abdalla, H.A. Evaluation of deflection in concrete members reinforced with fibre reinforced polymer (FRP) bars. Compos. Struct. 2002, 56, 63–71. [Google Scholar] [CrossRef]
- Ferdous, W.; Manalo, A.; Aravinthan, T. Effect of beam orientation on the static behaviour of phenolic core sandwich composites with different shear span-to-depth ratios. Compos. Struct. 2017, 168, 292–304. [Google Scholar] [CrossRef]
- Manalo, A. Behaviour of fibre composite sandwich structures under short and asymmetrical beam shear tests. Compos. Struct. 2013, 99, 339–349. [Google Scholar] [CrossRef]
- Maranan, G.; Manalo, A.; Benmokrane, B.; Karunasena, W.; Mendis, P. Evaluation of the flexural strength and serviceability of geopolymer concrete beams reinforced with glass-fibre-reinforced polymer (GFRP) bars. Eng. Struct. 2015, 101, 529–541. [Google Scholar] [CrossRef]
- Bouguerra, K.; Ahmed, E.; El-Gamal, S.; Benmokrane, B. Testing of full-scale concrete bridge deck slabs reinforced with fibre-reinforced polymer (FRP) bars. Constr. Build. Mater. 2011, 25, 3956–3965. [Google Scholar] [CrossRef]
- ACI. ACI Guide for the Design and Construction of Concrete Reinforced with FRP Bars; Report 440R-96; ACI: Detroit, MI, USA, 2001; pp. 1023–1034. [Google Scholar]
- ACI. State-of-the-Art Report on Fibre Reinforced Plastic (FRP) Reinforcement for Concrete Structures; ACI: Detroit, MI, USA, 2004. [Google Scholar]
- Grace, N.F.; Abdel-Sayed, G.; Ragheb, W.F. Strengthening of Concrete Beams Using Innovative Fibre-Reinforced Polymer Fabric. ACI Struct. J. 2002, 99, 692–700. [Google Scholar]
- Li, V.C.; Wang, S. Flexural behaviours of glass fibre reinforced polymer (GFRP) reinforced engineered cementitious composite beams. ACI Mater. J. 2002, 99, 11–20. [Google Scholar]
- Razaqpur, A.G.; Sevecova, D.; Cheung, M.S. Rational method for calculating deflection of fibre-reinforced polymer reinforced beams. ACI Struct. J. 2000, 97, 175–184. [Google Scholar]
- Sen, R.; Mullins, G.; Salem, T. Durability of E-glass/vinyl ester reinforcement in alkaline solution. ACI Struct. J. 2002, 99, 369–375. [Google Scholar]
- Chinnasamy, M.; Ajithkumar, R.; Singh, A.; Yangzom, D.; Parvati, T.; Joanna, P. Comparative study on the behaviour of textile reinforced concrete slab with engineered cementitious composite slab. Mater. Today Proc. 2020, 33, 1175–1180. [Google Scholar] [CrossRef]
- Laila, L.R.; Gurupatham, B.G.A.; Roy, K.; Lim, J.B.P. Effect of super absorbent polymer on microstructural and mechanical properties of concrete blends using granite pulver. Struct. Concr. 2020, 22, E898–E915. [Google Scholar] [CrossRef]
- He, Z.; Zhu, X.; Wang, J.; Mu, M.; Wang, Y. Comparison of CO2 emissions from OPC and recycled cement production. Constr. Build. Mater. 2019, 211, 965–973. [Google Scholar] [CrossRef]
- Sivaramakrishnan, R.; Anbarasu, E. Experimental Study on High-Performance Concrete by 40% Partial Replacement of Cementitious Material with Micro Silica, GGBS & Fly-Ash. IJESC 2020, 10, 25227–25231. [Google Scholar]
- Joanna, P.S.; Rooby, J.; Prabhavathy, A.; Preetha, R.; Pillai, C.S. Behaviour of reinforced concrete beams with 50 per cent fly ash. Int. J. Civ. Eng. Technol. 2013, 4, 36–48. [Google Scholar]
- Partha, S.D.; Pradip, N.; Prabir, K.S. Strength and Permeation Properties of Slag Blended Fly Ash Based Geopolymer Concrete. Adv. Mater. Res. 2013, 651, 168–173. [Google Scholar] [CrossRef]
- Nazari, A.; Riahi, S. Improvement compressive strength of concrete in different curing media by Al2O3 nanoparticles. Mater. Sci. Eng. A 2011, 528, 1183–1191. [Google Scholar] [CrossRef]
- Hosseini, P.; Hosseinpourpia, R.; Pajum, A.; Khodavirdi, M.M.; Izadi, H.; Vaezi, A. Effect of nano-particles and aminosilane interaction on the performances of cement-based composites: An experimental study. Constr. Build. Mater. 2014, 66, 113–124. [Google Scholar] [CrossRef]
- Maravelaki-Kalaitzaki, P.; Agioutantis, Z.; Lionakis, E.; Stavroulaki, M.; Perdikatsis, V. Physico-chemical and mechanical characterization of hydraulic mortars containing nano-titania for restoration applications. Cem. Concr. Compos. 2013, 36, 33–41. [Google Scholar] [CrossRef]
- Laila, L.R.; Gurupatham, B.G.A.; Roy, K.; Lim, J.B.P. Influence of super absorbent polymer on mechanical, rheological, durability, and microstructural properties of self-compacting concrete using non-biodegradable granite pulver. Struct. Concr. 2020, 22, E1093–E1116. [Google Scholar] [CrossRef]
- Rana, A.K.; Rana, S.; Kumari, A.; Kiran, V. Significance of nanotechnology in construction engineering. IJRTE 2009, 1, 46. [Google Scholar]
- Arezoumandi, M.; Volz, J.S.; Myers, J.J. Shear Behavior of High-Volume Fly Ash Concrete versus Conventional Concrete. J. Mater. Civ. Eng. 2013, 25, 1506–1513. [Google Scholar] [CrossRef]
- Rao, R.M.; Mohan, S.; Sekar, S.K. Shear Resistance of High Volume Fly ash Reinforced Concrete Beams without Web Reinforcement. Int. J. Civ. Struct. Eng. 2001, 1, 986–993. [Google Scholar]
- Agarwal, V.; Gupta, S.M.; Sachdeva, S.N. High volume fly ash concrete—A green concrete. J. Environ. Res. Dev. 2012, 6, 884–887. [Google Scholar]
- Lowe, D.; Roy, K.; Das, R.; Clifton, C.; Lim, J. Full-scale experiments on splitting behaviour of concrete slabs in steel-concrete composite beams with shear stud connection. Structures 2020, 23, 126–138. [Google Scholar] [CrossRef]
- Madan, C.S.; Munuswamy, S.; Joanna, P.S.; Gurupatham, B.G.A.; Roy, K. Comparison of the Flexural Behavior of High-Volume Fly AshBased Concrete Slab Reinforced with GFRP Bars and Steel Bars. J. Compos. Sci. 2022, 6, 157. [Google Scholar] [CrossRef]
- Kim, H.-K.; Lee, H. Use of power plant bottom ash as fine and coarse aggregates in high-strength concrete. Constr. Build. Mater. 2011, 25, 1115–1122. [Google Scholar] [CrossRef]
- Balakrishnan, B.; Awal, A.A. Mechanical Properties and Thermal Resistance of High Volume Fly Ash Concrete for Energy Efficiency in Building Construction. Key Eng. Mater. 2016, 678, 99–108. [Google Scholar] [CrossRef]
- Aravind Raj, P.S.; Divahar, R.; Sangeetha, S.P.; Naveen Kumar, K.; Ganesh, D.; Sabitha, S. Sustainable Development of Structural Joint made using High Volume Fly-Ash concrete. Int. J. Adv. Sci. Technol. 2020, 29, 6850–6857. [Google Scholar]
- Abadel, A.; Abbas, H.; Albidah, A.; Almusallam, T.; Al-Salloum, Y. Effectiveness of GFRP strengthening of normal and high strength fibre reinforced concrete after exposure to heating and cooling. Eng. Sci. Technol. Int. J. 2022, 36, 101147. [Google Scholar] [CrossRef]
- Shukla, S.; Waghmare, M.V. Strengthening of RC Column Using GFRP. Int. J. Res. Appl. Sci. Eng. Technol. 2022, 10, 1217–1224. [Google Scholar] [CrossRef]
- ANSYS Mechanical APDL Verification Set; ANSYS Inc.: Canonsburg, PA, USA, 2014.
- Sandrasekaran, S.; Praveen Kumar, A. Numerical Modeling of Square Steel Members Wrapped by CFRP Composites. Int. J. Innov. Technol. Explor. Eng. 2019, 8, 3082–3087. [Google Scholar] [CrossRef]
- Adam, M.A.; Erfan, A.M.; Habib, F.A.; El-Sayed, T.A. Structural Behavior of High-Strength Concrete Slabs Reinforced with GFRP Bars. Polymers 2021, 13, 2997. [Google Scholar] [CrossRef]
- Jayajothi, P.; Kumutha, R.; Vijai, K. Finite element analysis of FRP strengthened RC beams using Ansys. Asian J. Civ. Eng. 2013, 14, 631–642. [Google Scholar]
- Gherbi, A.; Dahmani, L.; Boudjemia, A. Study on two way reinforced concrete slab using Ansys with different boundary conditions and loading. World Acad. Sci. Eng. Technol. Int. J. Civ. Environ. Eng. 2018, 12, 1151–1156. [Google Scholar]

















| Materials/Type of Concrete | Cement | Fly Ash | Microsilica | M Sand | Aggregate | Water | Super Plasticiser (%) |
|---|---|---|---|---|---|---|---|
| OPC concrete | 1 | - | - | 2.16 | 3.42 | 0.5 | 0.3 |
| 60% HVFA | 0.4 | 0.6 | 0.1 | 2.1 | 3.32 | 0.5 | 0.3 |
| Chemical Composition | Content (% by Mass) |
|---|---|
| SiO2 | 52.52 |
| Al2O3 | 32.63 |
| Fe2O2 | 6.16 |
| SO3 | 4.95 |
| LOI | 1.08 |
| MnO | 0.03 |
| NAI-20 | 0.02 |
| Cao | Nil |
| Particulars | Specification |
|---|---|
| Aerial weight (GSM) | 400 |
| Tensile strength (N/mm2) | 2700 |
| Modulus of elasticity (kN/mm2) | 73 |
| Poisson’s ratio | 0.3 |
| The thickness of GFRP sheet (mm) | 1 |
| Elongation at break (%) | 5 |
| Fibre density (g/cm3) | 2.6 |
| Category | Slab Designation | Trial Numbers | Initial Crack Load (KN) | Ultimate Load (KN) | Modes of Failure |
|---|---|---|---|---|---|
| GROUP-I | GSC-2 | Trial 1 Trial 2 | 8.3 8.7 | 16.8 17.5 | Mode-II Mode-II |
| GSC-3 | Trial 1 Trial 2 | 14.2 14.7 | 23.7 24 | Mode-III Mode-III | |
| GSC-4 | Trial 1 Trial 2 | 6.7 6.3 | 16.4 15.5 | Mode-IV Mode-IV | |
| SRC | Trial 1 Trial 2 | 16.3 15.7 | 23.8 24 | Mode-I Mode-I | |
| GROUP-II | GSF-2 | Trial 1 Trial 2 | 5.9 5.7 | 17.1 16.7 | Mode-II Mode-II |
| GSF-3 | Trial 1 Trial 2 | 14.1 14 | 23.9 23.7 | Mode-II Mode-II | |
| GSF-4 | Trial 1 Trial 2 | 5.2 5.6 | 15.3 15.9 | Mode-IV Mode-IV | |
| SRF | Trial 1 Trial 2 | 18.5 19.1 | 27.3 28.5 | Mode-I Mode-I |
| Category | Slab Designation | Max. Load (Pu) (kN) | Ultimate Moment (MExp) (kNm) | Ultimate Strain in Concrete at Max Load % | Ultimate Strain in Reinforcement at Max Load % |
|---|---|---|---|---|---|
| GROUP-I | GSC-2 (1) | 16.8 | 2.24 | 0.31 | 0.36 |
| GSC-2 (2) | 17.5 | 2.33 | 0.31 | 0.39 | |
| GSC-3 (1) | 23.7 | 3.16 | 0.31 | 0.43 | |
| GSC-3 (2) | 24 | 3.20 | 0.31 | 0.43 | |
| GSC-4 (1) | 16.4 | 2.19 | 0.30 | 0.35 | |
| GSC-4 (2) | 15.5 | 2.07 | 0.30 | 0.34 | |
| SRC (1) | 23.8 | 3.17 | 0.29 | 2.01 | |
| SRC (2) | 24.0 | 3.20 | 0.31 | 1.91 | |
| GROUP-II | GSF-2 (1) | 17.1 | 2.28 | 0.31 | 0.36 |
| GSF-2 (2) | 16.7 | 2.22 | 0.30 | 0.36 | |
| GSF-3 (1) | 23.9 | 3.19 | 0.31 | 0.41 | |
| GSF-3 (2) | 23.7 | 3.16 | 0.31 | 0.42 | |
| GSF-4 (1) | 15.3 | 2.04 | 0.30 | 0.33 | |
| GSF-4 (2) | 15.9 | 2.12 | 0.30 | 0.33 | |
| SRF (1) | 27.3 | 3.70 | 0.30 | 2.03 | |
| SRF (2) | 28.5 | 3.64 | 0.31 | 2.19 |
| Specimen | Ultimate Load (kN) | Deflection at Mid-Span (mm) | ||
|---|---|---|---|---|
| Experimental | NLFEA (ANSYS) | Experimental | NLFEA (ANSYS) | |
| SRC | 24 | 23 | 16.2 | 15.9 |
| SRF | 28.5 | 27 | 17.9 | 16.4 |
| GSC-3 | 24 | 23.5 | 2.7 | 2.5 |
| GSF-3 | 23.9 | 23 | 2.4 | 2.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Madan, C.S.; Panchapakesan, K.; Anil Reddy, P.V.; Joanna, P.S.; Rooby, J.; Gurupatham, B.G.A.; Roy, K. Influence on the Flexural Behaviour of High-Volume Fly-Ash-Based Concrete Slab Reinforced with Sustainable Glass-Fibre-Reinforced Polymer Sheets. J. Compos. Sci. 2022, 6, 169. https://doi.org/10.3390/jcs6060169
Madan CS, Panchapakesan K, Anil Reddy PV, Joanna PS, Rooby J, Gurupatham BGA, Roy K. Influence on the Flexural Behaviour of High-Volume Fly-Ash-Based Concrete Slab Reinforced with Sustainable Glass-Fibre-Reinforced Polymer Sheets. Journal of Composites Science. 2022; 6(6):169. https://doi.org/10.3390/jcs6060169
Chicago/Turabian StyleMadan, Chinnasamy Samy, Krithika Panchapakesan, Potlapalli Venkata Anil Reddy, Philip Saratha Joanna, Jessy Rooby, Beulah Gnana Ananthi Gurupatham, and Krishanu Roy. 2022. "Influence on the Flexural Behaviour of High-Volume Fly-Ash-Based Concrete Slab Reinforced with Sustainable Glass-Fibre-Reinforced Polymer Sheets" Journal of Composites Science 6, no. 6: 169. https://doi.org/10.3390/jcs6060169







