Validation of Deep Learning Segmentation of CT Images of Fiber-Reinforced Composites
Abstract
:1. Introduction
2. Material and Imaging


3. Analysis Methods
3.1. Image Segmentation and Correlation
3.2. Measurements of Fiber Coating Thicknesses
4. Results
4.1. Deep Learning Segmentation Validation
4.1.1. Ground Truth from Synthetic Data
4.1.2. Ground Truth from Manually Segmented CT Images
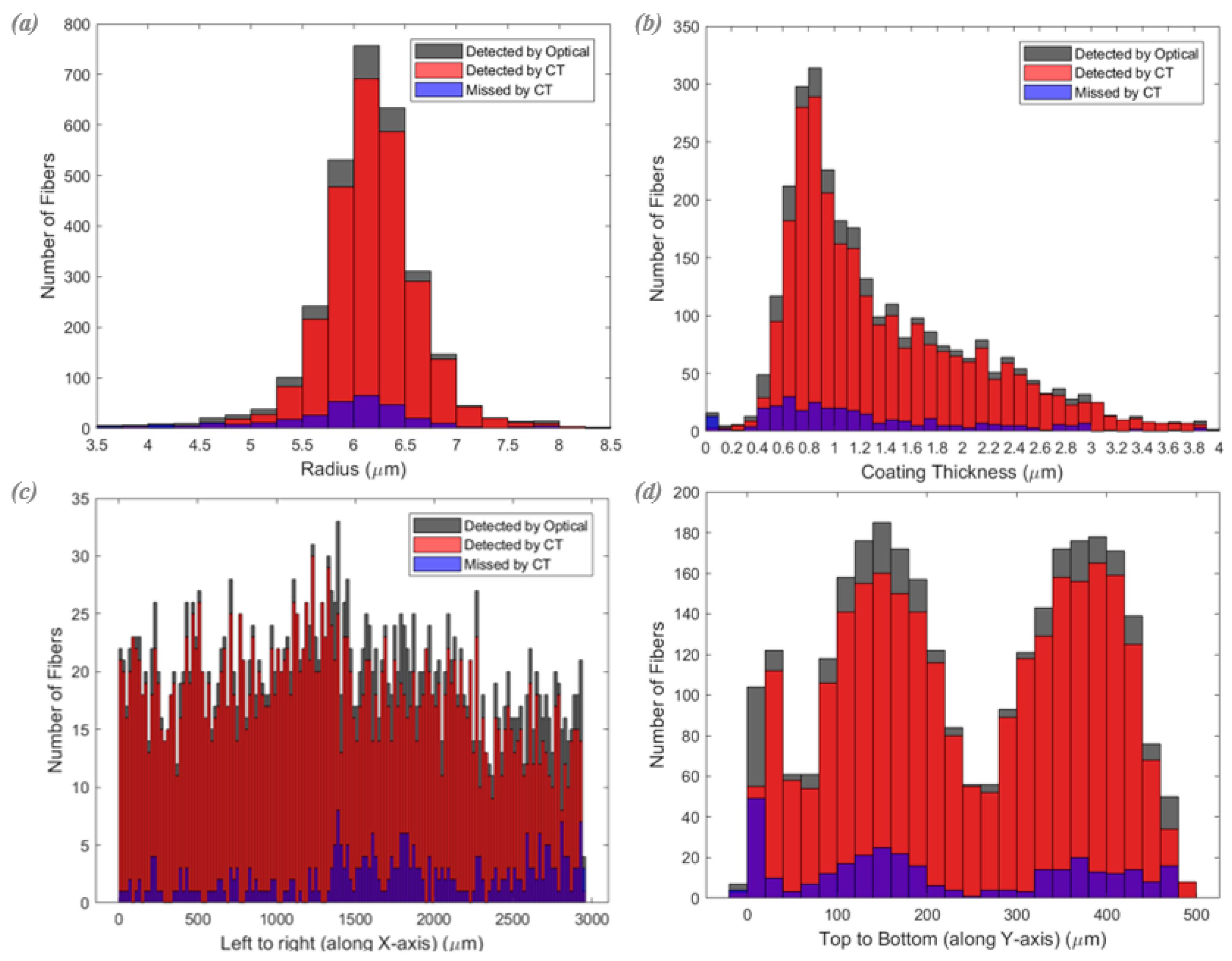
4.1.3. Ground Truth from High-Resolution Optical Images
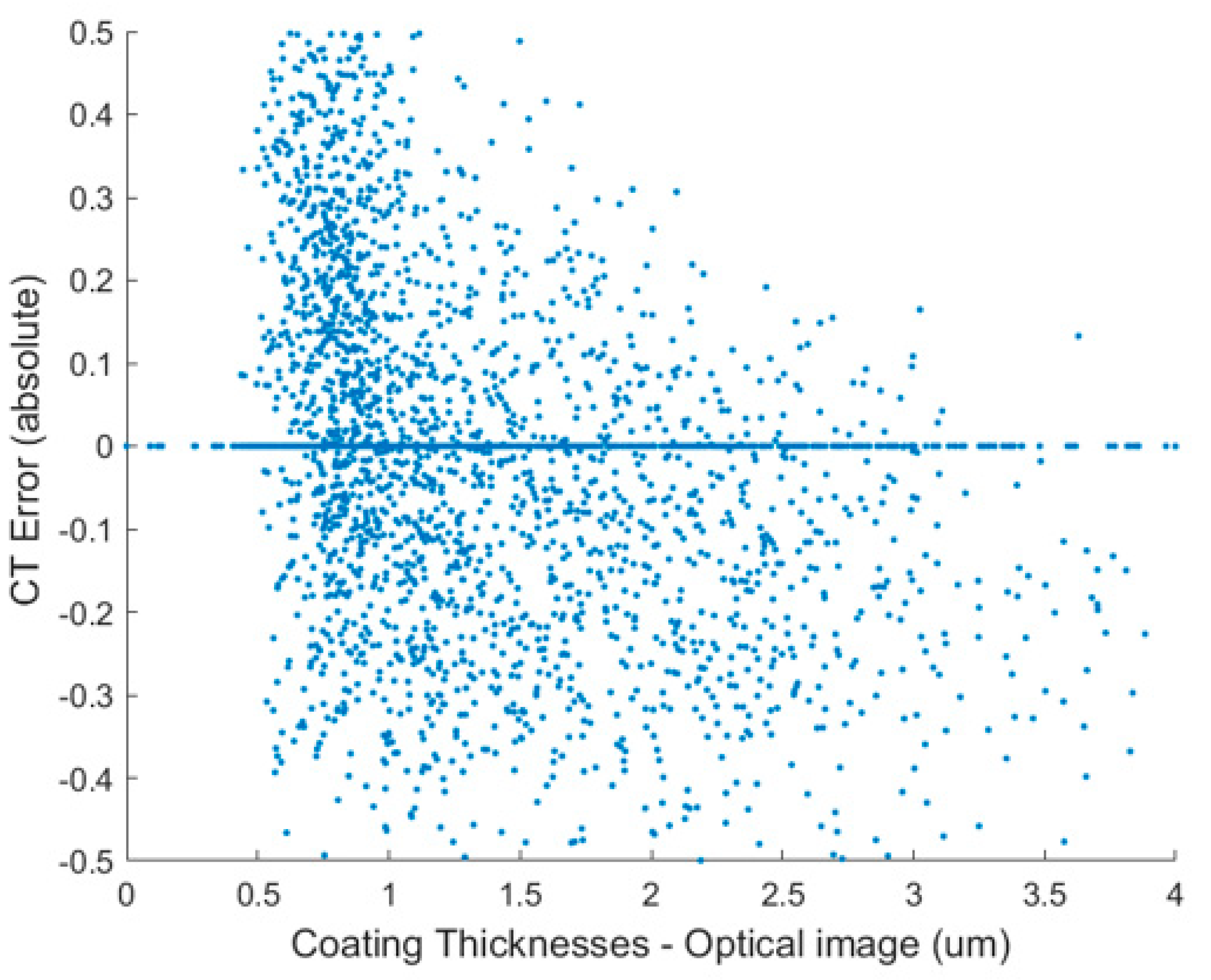
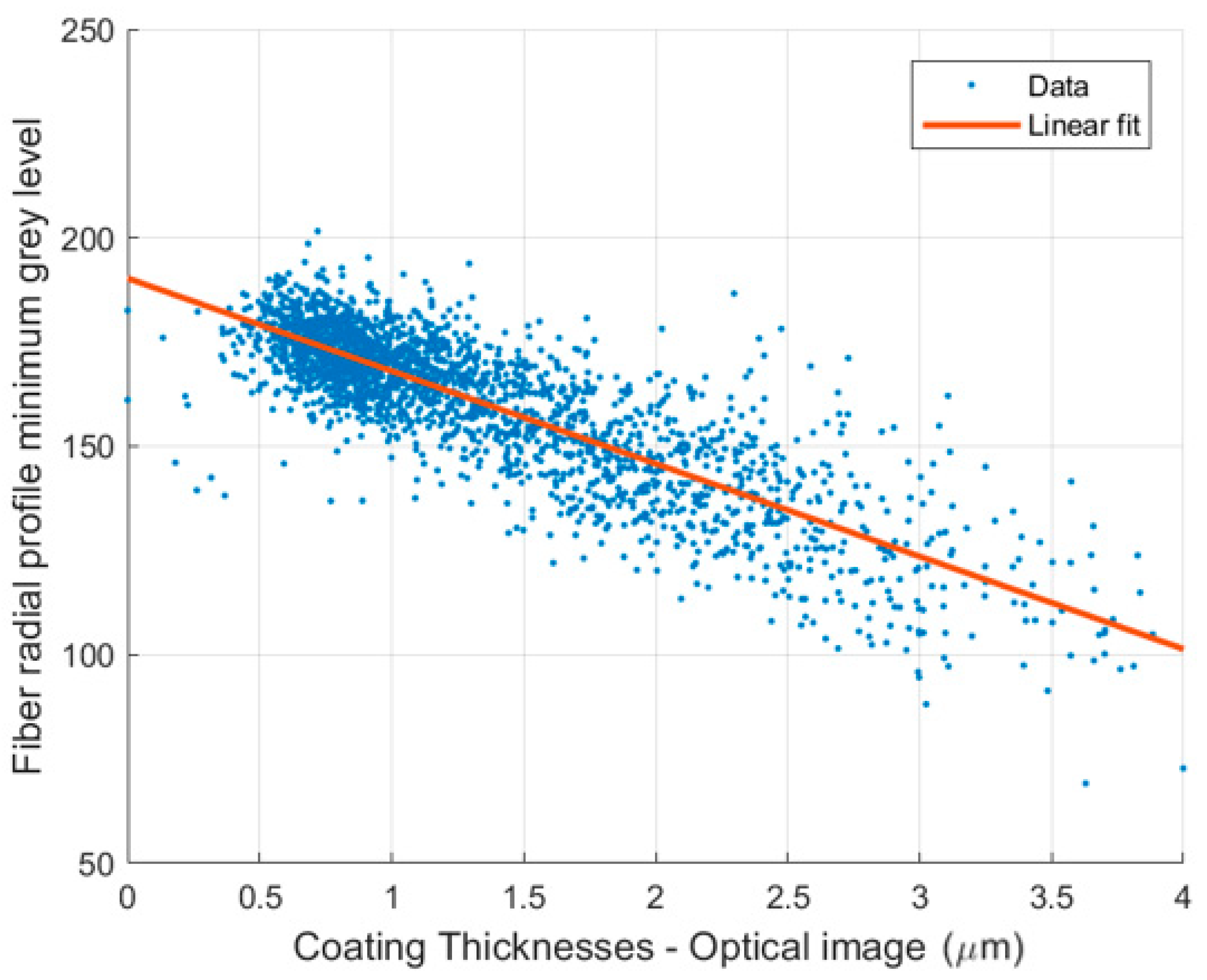
4.2. Calibration of CT Measurements of Coating Thickness with Optical Measurements
5. Discussion
5.1. Ground Truth from Synthetic Data
5.2. Ground Truth from Manually Segmented Images
5.3. Ground Truth from High-Resolution Optical Images
5.4. Measurements from CT Image
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Details of Analysis Methods
Appendix A.1. Deep Learning Image Segmentation

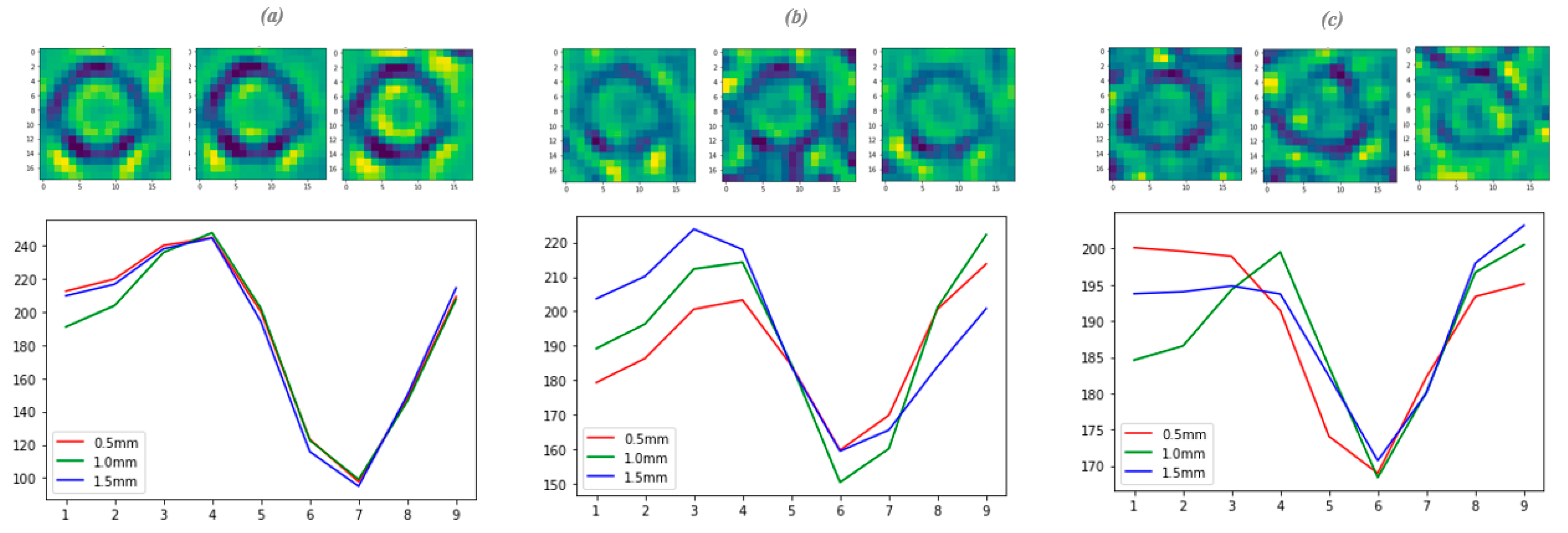
Appendix A.2. Hough Transform

References
- Bale, H.A.; Blacklock, M.; Begley, M.R.; Marshall, D.B.; Cox, B.N.; Ritchie, R.O. Characterizing three-dimensional textile ceramic composites using synchrotron x-ray micro-computed-tomography. J. Am. Ceram. Soc. 2012, 95, 392–402. [Google Scholar] [CrossRef]
- Bale, H.A.; Haboub, A.; Macdowell, A.A.; Nasiatka, J.R.; Parkinson, D.Y.; Cox, B.N.; Marshall, D.B.; Ritchie, R.O. Real-time quantitative imaging of failure events in materials under load at temperatures above 1600 °C. Nat. Mater. 2013, 12, 40–46. [Google Scholar] [CrossRef]
- Chateau, C.; Gélébart, L.; Bornert, M.; Crépin, J.; Boller, E.; Sauder, C.; Ludwig, W. In situ X-ray microtomography characterization of damage in SiCf/SiC minicomposites. Compos. Sci. Technol. 2011, 71, 916–924. [Google Scholar] [CrossRef] [Green Version]
- Wright, P.; Moffat, A.; Sinclair, I.; Spearing, S.M.; High, S.M.S. High resolution tomographic imaging and modelling of notch tip damage in a laminated composite. Compos. Sci. Technol. 2012, 70, 1444–1452. [Google Scholar] [CrossRef] [Green Version]
- Mazars, V.; Caty, O.; Couégnat, G.; Bouterf, A.; Roux, S.; Denneulin, S.; Pailhès, J.; Vignoles, G.L. Damage investigation and modeling of 3D woven ceramic matrix composites from X-ray tomography in-situ tensile tests. Acta Mater. 2017, 140, 130–139. [Google Scholar] [CrossRef] [Green Version]
- Cox, B.N.; Bale, H.A.; Begley, M.R.; Blacklock, M.; Do, B.-C.; Fast, T.; Naderi, M.; Novak, M.D.; Rajan, V.P.; Rinaldi, R.G.; et al. Stochastic Virtual Tests for High-Temperature Ceramic Matrix Composites. Annu. Rev. Mater. Res. 2014, 44, 479–529. [Google Scholar] [CrossRef]
- Saucedo-Mora, L.; Lowe, T.; Zhao, S.; Lee, P.D.; Mummery, P.M.; Marrow, T.J. In situ observation of mechanical damage within a SiC-SiC ceramic matrix composite. J. Nucl. Mater. 2016, 481, 13–23. [Google Scholar] [CrossRef]
- Barnard, H.S.; MacDowell, A.A.; Parkinson, D.Y.; Mandal, P.; Czabaj, M.W.; Gao, Y.; Maillet, E.; Blank, B.; Larson, N.M.; Ritchie, R.O.; et al. Synchrotron X-ray micro-tomography at the Advanced Light Source: Developments in high-temperature in-situ mechanical testing. J. Phys. Conf. Ser. 2017, 849. [Google Scholar] [CrossRef] [Green Version]
- Larson, N.M.; Cuellar, C.; Zok, F.W. X-ray computed tomography of microstructure evolution during matrix impregnation and curing in unidirectional fiber beds. Compos. Part A Appl. Sci. Manuf. 2019, 117, 243–259. [Google Scholar] [CrossRef]
- Garcea, S.C.; Wang, Y.; Withers, P.J. X-ray computed tomography of polymer composites. Compos. Sci. Technol. 2018, 156, 305–319. [Google Scholar] [CrossRef]
- Mardia, K.V.; Hainsworth, T.J. A Spatial Thresholding Method for Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 1988, 10, 919–927. [Google Scholar] [CrossRef]
- Pham, D.L.; Xu, C.; Prince, J.L. Current Methods in Medical Image Segmentation. Ann. Rev. Biomed. Eng. 2000, 2, 315–337. [Google Scholar] [CrossRef] [PubMed]
- Perciano, T.; Ushizima, D.M.; Krishnan, H.; Parkinson, D.Y.; Larson, N.M.; Pelt, D.M.; Bethel, W.; Zok, F.W.; Sethian, J. Insight into 3D micro-CT data: Exploring segmentation algorithms through performance metrics. J. Synchrotron Radiat. 2017, 24, 1065–1077. [Google Scholar] [CrossRef] [PubMed]
- Straumit, I.; Lomov, S.V.; Wevers, M. Quantification of the internal structure and automatic generation of voxel models of textile composites from X-ray computed tomography data. Compos. Part A Appl. Sci. Manuf. 2015, 69, 150–158. [Google Scholar] [CrossRef]
- Ushizima, D.; Perciano, T.; Krishnan, H.; Loring, B.; Bale, H.A.; Parkinson, D.Y.; Sethian, J. Structure recognition from high resolution images of ceramic composites. In Proceedings of the 2014 IEEE International Conference on Big Data, Washington, DC, USA, 27–30 October 2014; pp. 683–691. [Google Scholar] [CrossRef] [Green Version]
- Czabaj, M.W.; Riccio, M.L.; Whitacre, W.W. Numerical reconstruction of graphite/epoxy composite microstructure based on sub-micron resolution X-ray computed tomography. Compos. Sci. Technol. 2014, 105, 174–182. [Google Scholar] [CrossRef]
- Emerson, M.J.; Jespersen, K.M.; Dahl, A.B.; Conradsen, K.; Mikkelsen, L.P. Individual fibre segmentation from 3D X-ray computed tomography for characterising the fibre orientation in unidirectional composite materials. Compos. Part A Appl. Sci. Manuf. 2017, 97, 83–92. [Google Scholar] [CrossRef]
- Badran, A.; Marshall, D.B.; Legault, Z.; Makovetsky, R.; Provencher, B.; Piché, N.; Marsh, M. Automated segmentation of computed tomography images of fiber-reinforced composites by deep learning. J. Mater. Sci. 2020, 55, 16273–16289. [Google Scholar] [CrossRef]
- Creveling, P.J.; Whitacre, W.W.; Czabaj, M.W. A fiber-segmentation algorithm for composites imaged using X-ray microtomography: Development and validation. Compos. Part A Appl. Sci. Manuf. 2019, 126, 105606. [Google Scholar] [CrossRef]
- Sinchuk, Y.; Kibleur, P.; Aelterman, J.; Boone, M.N.; Paepegem, W. Van Geometrical and Deep Learning Approaches for Instance Segmentation of CFRP Fiber Bundles in Textile Composites. Compos. Struct. 2021, 277, 114626. [Google Scholar] [CrossRef]
- Emerson, M.J.; Dahl, V.A.; Conradsen, K.; Mikkelsen, L.P.; Dahl, A.B. Statistical validation of individual fibre segmentation from tomograms and microscopy. Compos. Sci. Technol. 2018, 160, 208–215. [Google Scholar] [CrossRef]
- Padture, N.P. Advanced structural ceramics in aerospace propulsion. Nat. Mater. 2016, 15, 804–809. [Google Scholar] [CrossRef] [PubMed]
- Zok, F.W. Ceramic-matrix composites enable revolutionary gains in tubeine engine efficiency. Am. Ceram. Soc. Bull. 2016, 95, 22–28. [Google Scholar]
- Spitsberg, I.; Steibel, J. Thermal and Environmental Barrier Coatings for SiC/SiC CMCs in Aircraft Engine Applications. Int. J. Appl. Ceram. Technol. 2004, 1, 291–301. [Google Scholar] [CrossRef]
- Steibel, J. Ceramic Matrix Composites Taking Flight at GE Aviation, (n.d.). Available online: www.ceramics.org (accessed on 16 September 2021).
- Hilmas, A.M.; Sevener, K.M.; Halloran, J.W. Damage evolution in SiC/SiC unidirectional composites by X-ray tomography. J. Am. Ceram. Soc. 2020, 103, 3436–3447. [Google Scholar] [CrossRef]
- Maillet, E.; Singhal, A.; Hilmas, A.M.; Gao, Y.; Zhou, Y.; Henson, G.; Wilson, G. Combining in-situ synchrotron X-ray microtomography and acoustic emission to characterize damage evolution in ceramic matrix composites. J. Eur. Ceram. Soc. 2019, 39, 3546–3556. [Google Scholar] [CrossRef]
- Haboub, A.; Bale, H.A.; Nasiatka, J.R.; Cox, B.N.; Marshall, D.B.; Ritchie, R.O.; Macdowell, A.A. Tensile testing of materials at high temperatures above 1700 °C with in situ synchrotron X-ray micro-tomography. Rev. Sci. Instrum. 2014, 85, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Brada, R.S.; Ron Wein, R.; Wilson, G.; Santamaria-Pang, A.; Gugel, L. Multi-Stage Segmentation using Synthetic Images. U.S. Patent 10991101, 27 April 2021. [Google Scholar]
- Creveling, P.J.; Whitacre, W.; Czabaj, M. Synthetic X-ray Microtomographic Image Data of Fiber-Reinforced Composites. 2019. Available online: https://materialsdata.nist.gov/handle/11256/988 (accessed on 9 June 2021).
- Ros, G.; Sellart, L.; Materzynska, J.; Vazquez, D.; Lopez, A.M. The Synthia Dataset: A Large Collection of Synthetic Images for Semantic Segmentation of Urban Scenes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 3234–3243. [Google Scholar]
- Hinterstoisser, S.; Lepetit, V.; Wohlhart, P.; Konolige, K. On Pre-Trained Image Features and Synthetic Images for Deep Learning. In Proceedings of the European Conference on Computer Vision (ECCV) Workshops 2018, Munich, Germany, 8–14 September 2018. [Google Scholar]
- Badran, A.; Marshall, D.B.; Maillet, E. Effect of Microstructural Variability on Matrix Cracking and Fiber Fracture in Unidirectional SiC-SiC Composites. Unpublished work. 2022; in preparation. [Google Scholar]
- Badran, A.; Marshall, D.B.; Legault, Z.; Makovetsky, R.; Provencher, B.; Piché, N.; Marsh, M. XCT dataset and Deep Learning Models for Automated Segmentation of Computed Tomography Images of Fiber-Reinforced Composites. Mater. Data Facil. Open 2020. [Google Scholar] [CrossRef]





| Metric | ||||||
|---|---|---|---|---|---|---|
| Method | Detection Rate % | Precision % | Recall % | Accuracy % | DICE % | IOU % |
| Synthetic | 100 | 99.8 | 99.6 | 100 | 99.7 | 99.5 |
| GT from Manual | 89.6 | 93.9 | 86.5 | 76.2 | 93.3 | 80.6 |
| GT from Optical | 93.7 | 88.4 | 89.2 | NA | 88.8 | 80.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Badran, A.; Parkinson, D.; Ushizima, D.; Marshall, D.; Maillet, E. Validation of Deep Learning Segmentation of CT Images of Fiber-Reinforced Composites. J. Compos. Sci. 2022, 6, 60. https://doi.org/10.3390/jcs6020060
Badran A, Parkinson D, Ushizima D, Marshall D, Maillet E. Validation of Deep Learning Segmentation of CT Images of Fiber-Reinforced Composites. Journal of Composites Science. 2022; 6(2):60. https://doi.org/10.3390/jcs6020060
Chicago/Turabian StyleBadran, Aly, Dula Parkinson, Daniela Ushizima, David Marshall, and Emmanuel Maillet. 2022. "Validation of Deep Learning Segmentation of CT Images of Fiber-Reinforced Composites" Journal of Composites Science 6, no. 2: 60. https://doi.org/10.3390/jcs6020060






