Two-Dimensional Shallow-Water Model with Porosity for Urban Flood Modeling ^†

Abstract

In the world, floods are at the forefront of natural hazard. Urban areas are often at risk of flooding and just as often unprepared for management. Flood modeling is nowadays a very important topic in the theme of water, it inevitably involves the numerical resolution of the shallow water equations derived from the Navier Stocks equations governing flows. Two-dimensional shallow water models with porosity appear as an interesting path for the large-scale modeling of floodplains with urbanized areas. The porosity accounts for the reduction in storage and in the exchange sections due to the presence of buildings and other structures in the floodplain. The introduction of a porosity into the two-dimensional shallow water equations leads to modified expressions for the fluxes and source terms. An extra source term appears in the momentum equation. The developed solution method consists in solving the two-dimensional shallow water equations with porosity via a finite volume scheme solving the conservative form of the equations which can be reduced to a calculation of flux through an edge, a problem that can be approached by a one-dimensional problem in the normal direction at the edge (Riemann problem).

1. Introduction

The theme of this work concerns the control of floods and inundation, especially in the case of sudden events: dam break. Urban areas are often exposed to these flood risks (presence of watercourses, impervious surfaces) but also often poorly prepared to manage these risks. Numerical modeling makes it possible to map flows in a given site, with different possible applications: knowledge of risk exposure, regulation of urban development, definitions of crisis management scenarios. Models of shallow water equations with porosity were initially proposed by Defina et al. [1] and Hervouet et al. [2]. In this work, we present a numerical model with porosity for the simulation of free surface flows. To do this, we adopt a finite volume method based on the resolution of the conservative form of the shallow water equations, a problem that can be approached by a one-dimensional problem in the normal direction at the edge (Riemann problem). The algorithm comprises two steps: a predictor step for the discretization of the gradient terms and a corrective step for the processing of the source terms. The digital flows at the interfaces of each control volume are reconstructed using biassed scheme. The proposed method is implemented on unstructured meshes. As an application, the solver is tested for dam break study.

2. Material and Methods

2.1. Mathematical Model

The resolution method consists in solving two-dimensional shallow water equations using a finite volume scheme solving the conservative form of equations on an unstructured mesh composed of quadrilaterals and triangles.

The shallow water equations are written in conservative form with the concept of porosity in the form [Soares-Frazão] [3]:

$$\frac{\partial W}{\partial t}+\frac{\partial f_1}{\partial x}+\frac{\partial f_2}{\partial y}=S$$

(1)

with

$$W=\left[\begin{array}{c}\varphi h\\ \varphi hu\\ \varphi hv\end{array}\right] f_1=\left[\varphi \begin{array}{c}\varphi hu\\ h{u}^2+\varphi \frac{g{h}^2}{2}\\ \varphi huv\end{array}\right] f_2=\left[\begin{array}{c}\varphi hv\\ \varphi huv \\ \varphi h{v}^2+\varphi \frac{g{h}^2}{2}\end{array}\right] S=\left[\begin{array}{c}0\\ S_{p,x} \\ S_{p,y}\end{array}\right]$$

(2)

where ϕ is the porosity, g is the gravitational acceleration, h is the water depth, u and v are the velocities in the x and y directions, S_p,x and S_p,y are the source terms resulting from the variations in the bottom slope and variations of porosity in the directions x and y.

The source terms are given by:

$$S_{p,x}=\varphi gh S_{0,x}+g\frac{h^2}{2}\frac{\partial \varphi }{\partial x}=-\varphi gh\frac{\partial z}{\partial x}+g\frac{h^2}{2}\frac{\partial \varphi }{\partial x}$$

(3)

$$S_{p,y}=\varphi gh S_{0,y}+g\frac{h^2}{2}\frac{\partial \varphi }{\partial y}=-\varphi gh\frac{\partial z}{\partial y}+g\frac{h^2}{2}\frac{\partial \varphi }{\partial y}$$

(4)

z is the dimension of the bottom, and S_0,x, S_0,y are the source terms of the bottom slope in the x and y directions.

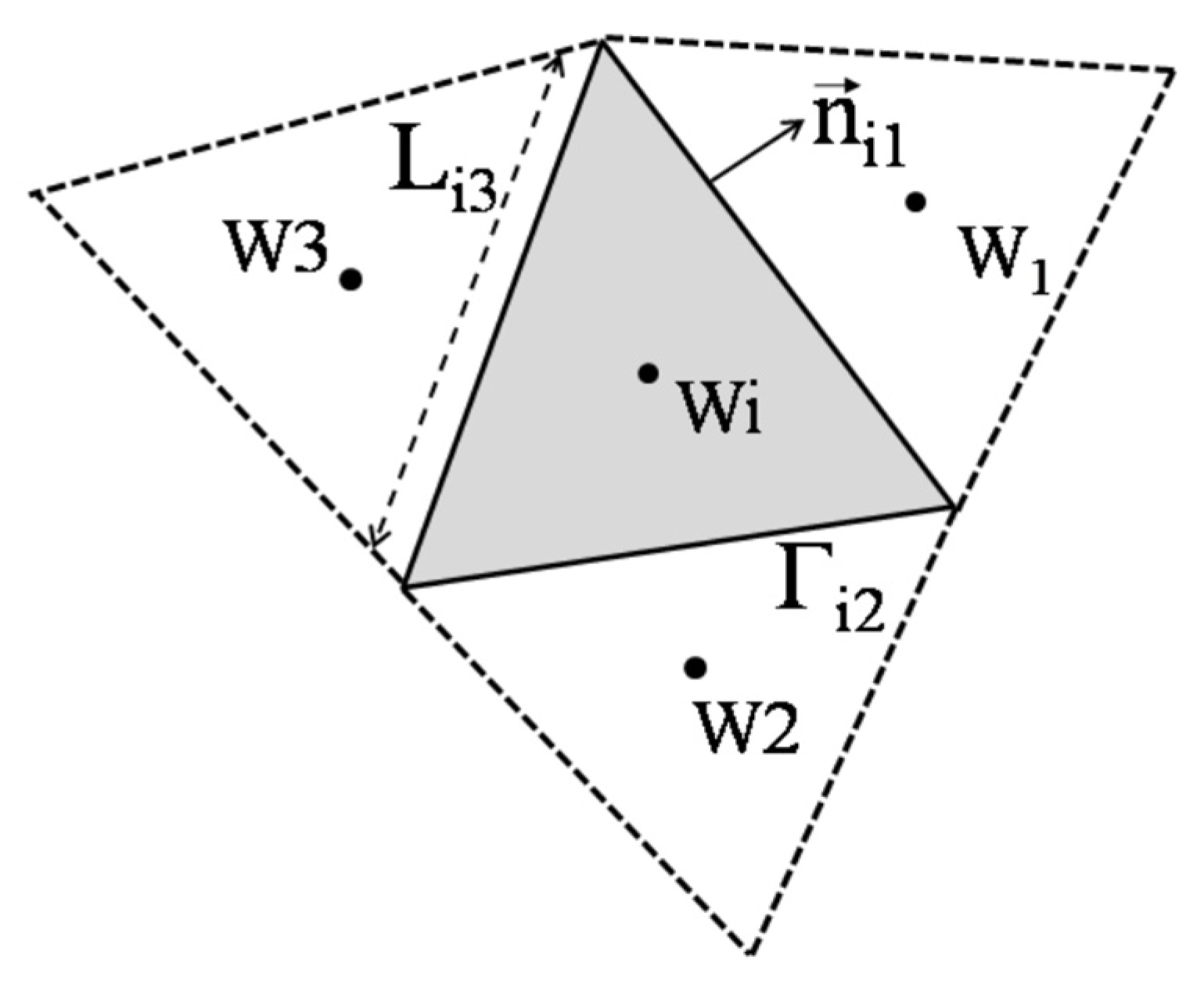
2.2. Numerical Methods

This is a widely used technique for the numerical resolution of fluid flow equations. This method relies on the integral discretization of the equations and requires the subdivision of the domain into a finite number of cells called control volume. The integral is applicable locally on each control volume and keeps the same value in each calculation cell. In our case, the domain of computation is discretized in triangular mesh and the control volumes are defined by the triangles T_i of the mesh. We speak of formulation finite volume (see Figure 1).

The integration of the system (1) on each control volume T_i and the use of the Green divergence formula make it possible to write:

$${{\displaystyle \int }}_{T_i}\frac{\partial W}{\partial t}dV+{\displaystyle \sum }_{j\in N\left(i\right)}{{\displaystyle \int }}_{{\mathsf{\Gamma }}_{ij}}{f}_1\left(W, n\right)d\sigma ={{\displaystyle \int }}_{T_i}S\left(W\right)dV$$

(5)

where N(i) denotes the set of neighboring triangles of T_i per edge and Γ_ij the edge separating two neighboring triangles T_i and T_j.

3. Results and Discussion

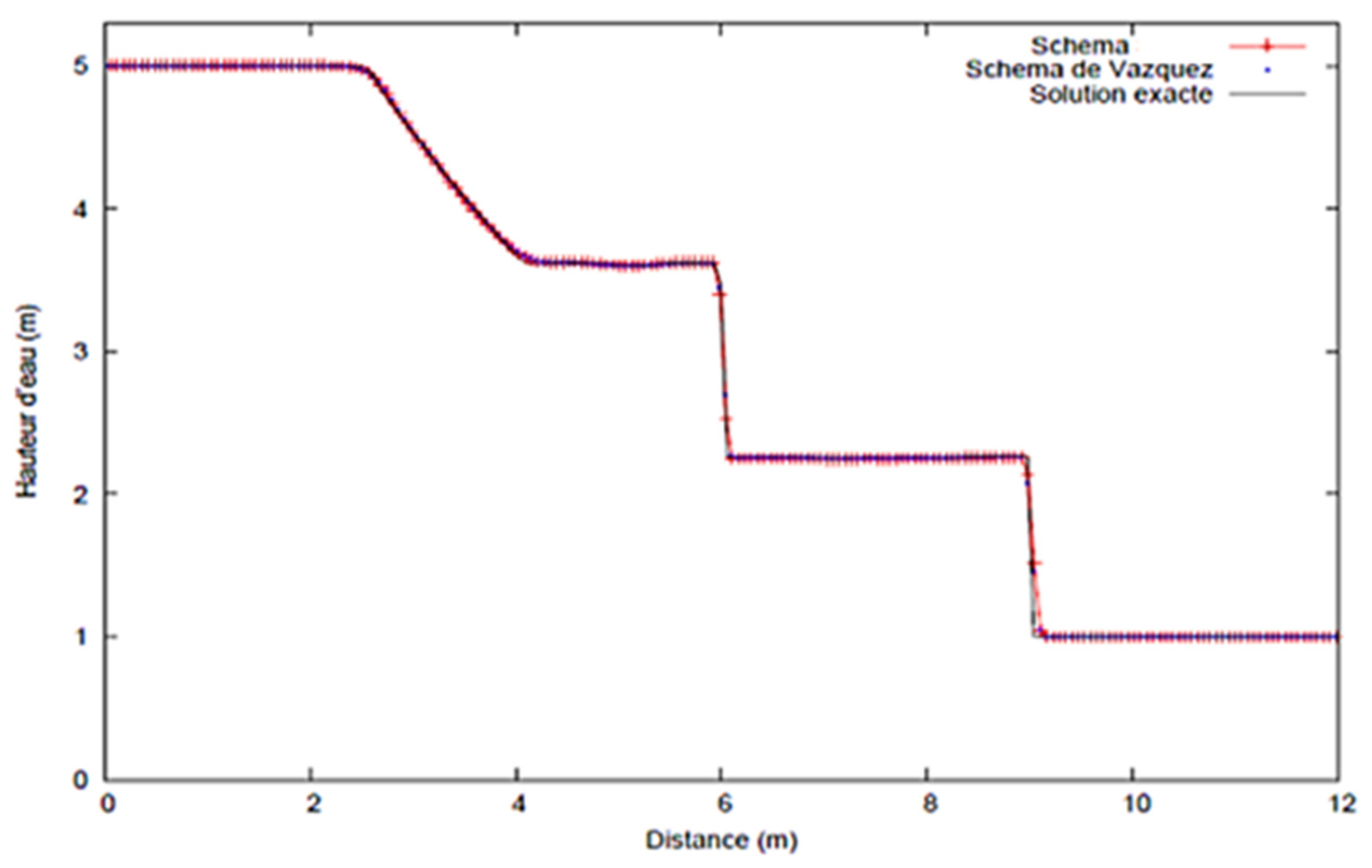
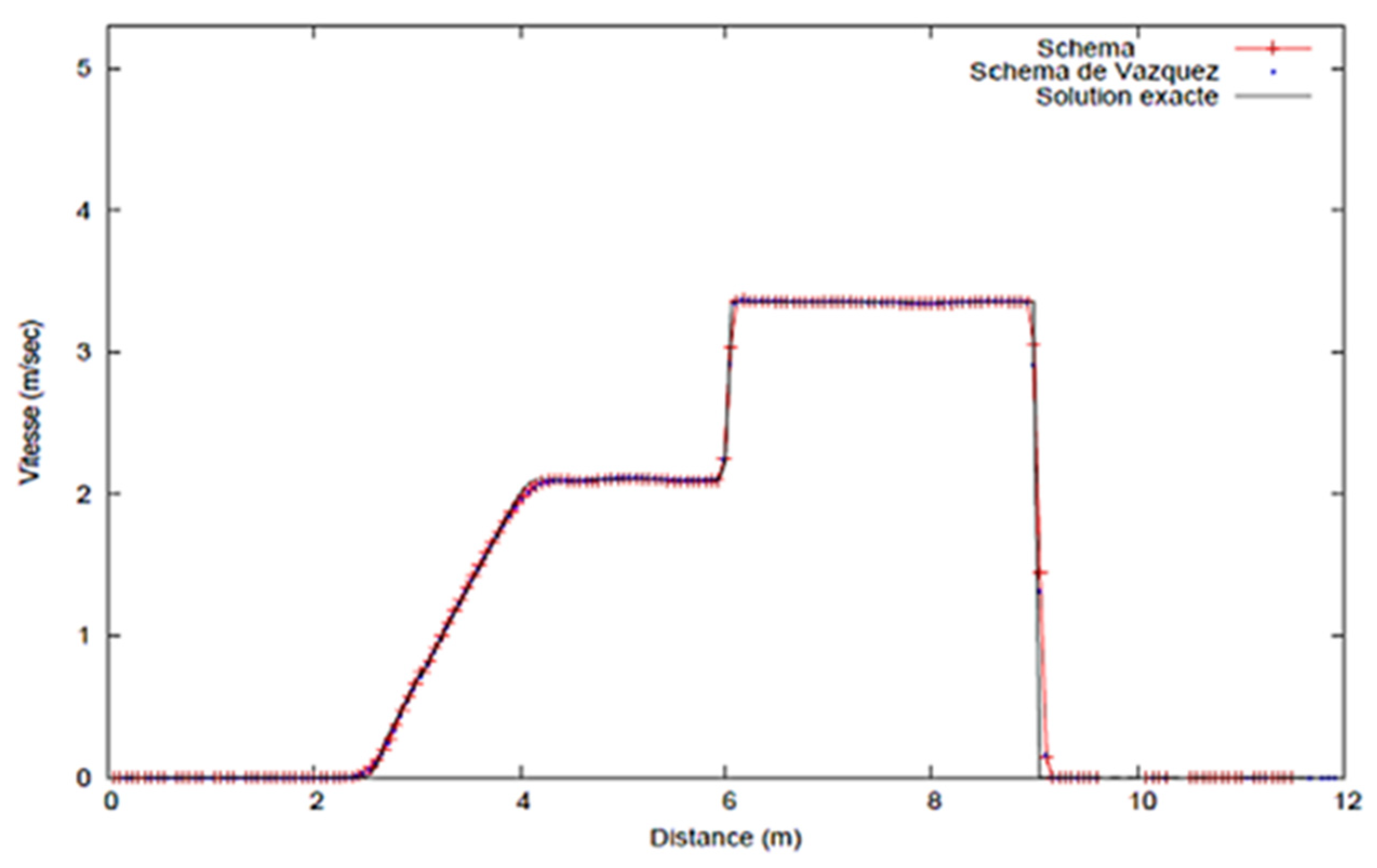
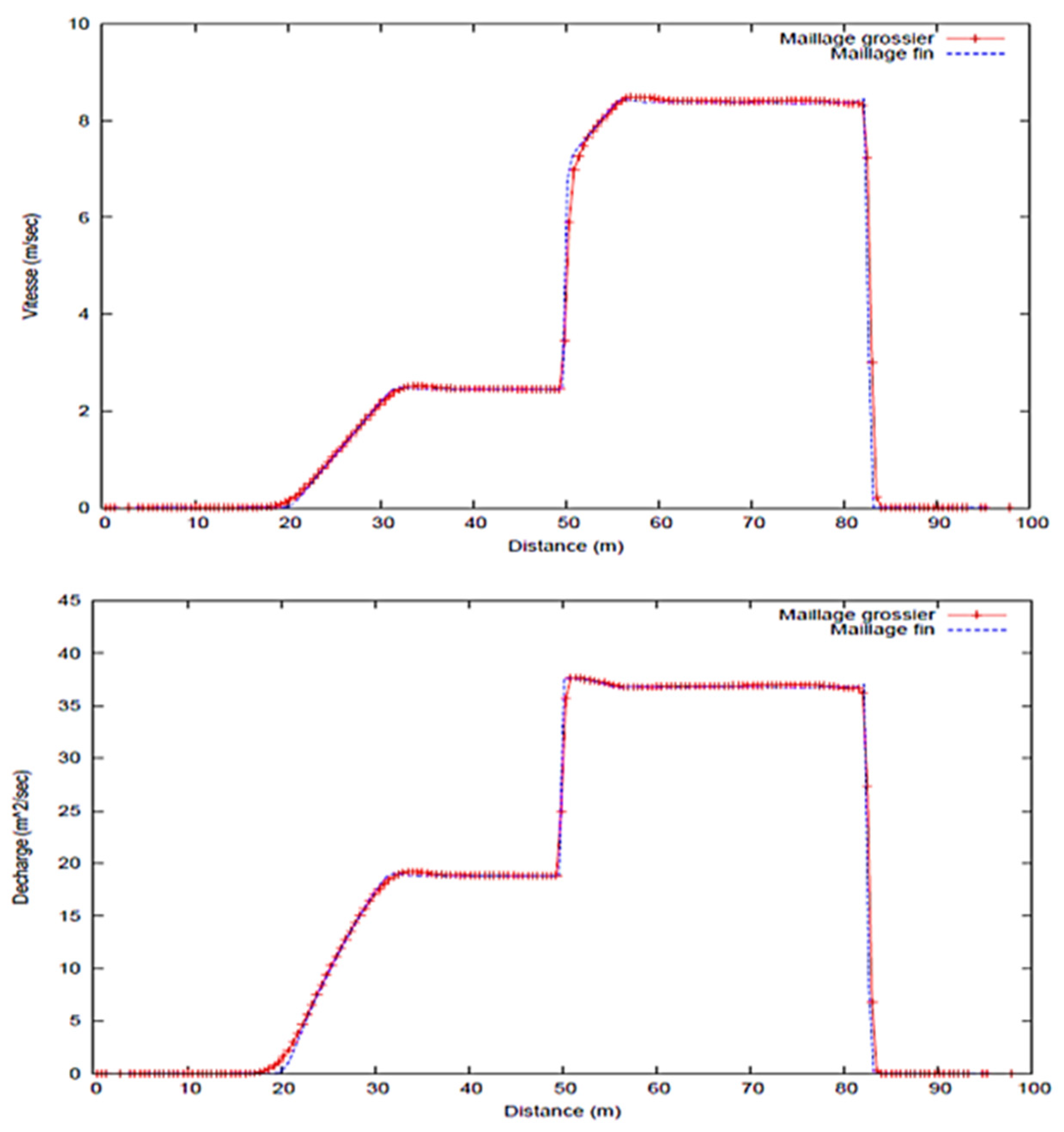
3.1. Dam Break with Constant Porosity

This first test case consists of a dam break in a rectangular channel with a constant porosity ϕ = 1. The channel length is L = 12 m and the break occurs at x₀ = 6 m. The channel mesh is unstructured and consists of 3257 knots and 4328 triangles. The bottom has the form of a step, it is defined by:

$$Z\left(x,y\right)=\{\begin{array}{c}0 \mathrm{m} si x\le x_0 \\ 1 \mathrm{m} si x>x_0 \end{array}$$

In the initial state, the flow is assumed at repose (u = v = 0 m/s) and the water height is:

$$h\left(x,y,0\right)=\{\begin{array}{c}5 \mathrm{m} si x\le x_0 \\ 1 \mathrm{m} si x>x_0 \end{array}$$

The exact solution of this problem consists of a rarefaction wave moving with a negative velocity, a nonlinear discontinuity on the step and a shock wave moving with a positive velocity. Figure 2 show comparisons between our solution and that of Vazquez’s equilibrium scheme [4] and the exact solution at physical time t = 0.5 s. These figures clearly show a very high precision of the schema and a very good agreement with the exact solution.

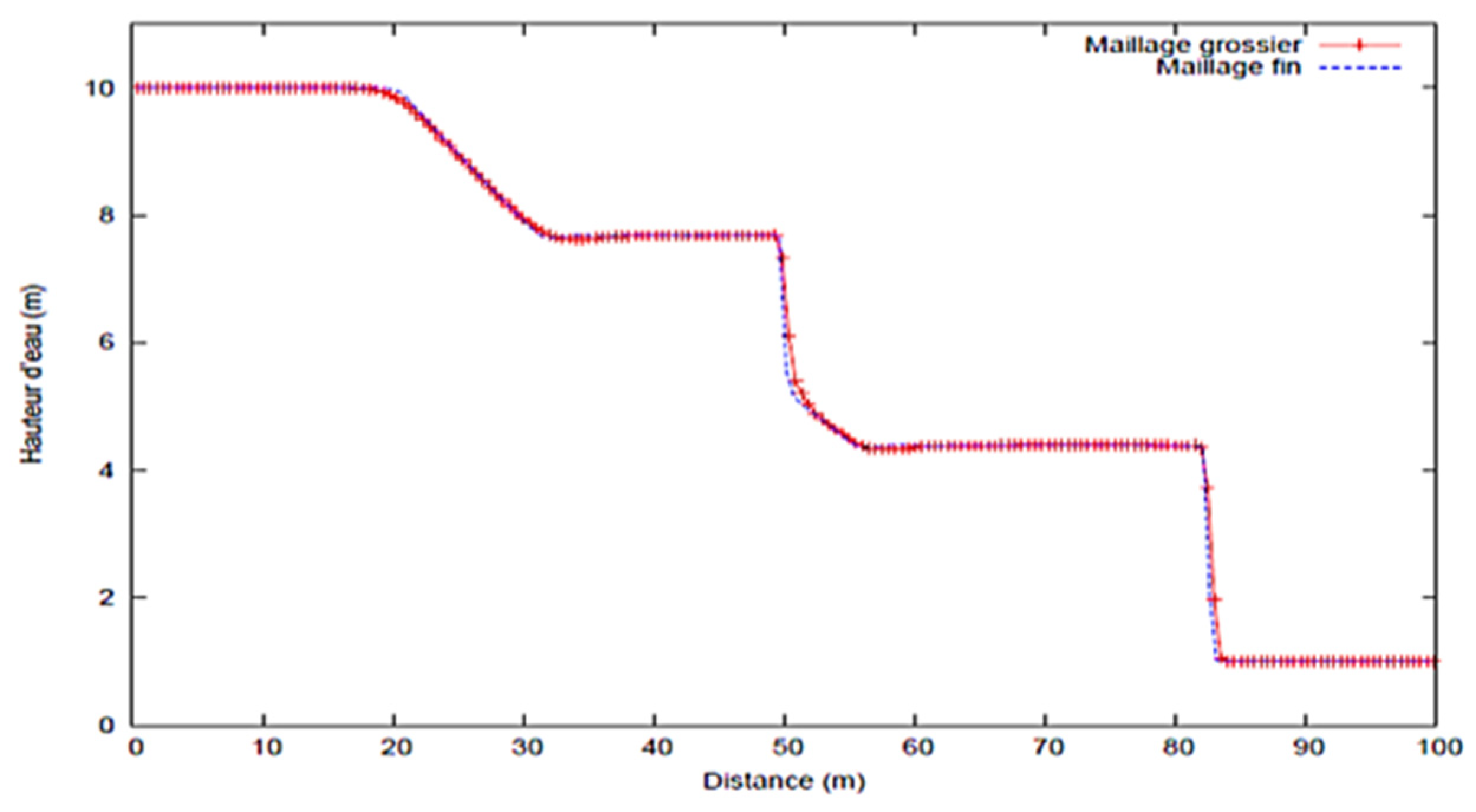
3.2. Dam Break with Variable Porosity

This test consists of a dam break in a rectangular channel with a constant bottom, but this time with discontinuous porosity ϕ. The channel length is L = 100 m and the break occurs at x₀ = 50 m. The porosity is:

$$\varphi \left(x,y\right)=\{\begin{array}{c}1 si x\le x_0 \\ 0.5 si x>x_0 \end{array}$$

and the height of water in the initial state is:

$$\mathit{h}\left(\mathit{x},\mathit{y},\mathit{0}\right)=\{\begin{array}{c}\mathit{10} \mathrm{m} \mathit{s}\mathit{i} \mathit{x}\le {\mathit{x}}_{\mathit{0}} \\ \mathit{1} \mathrm{m} \mathit{s}\mathit{i}\mathit{ }\mathit{x}>{\mathit{x}}_{\mathit{0}} \end{array}$$

Note that the solution for this problem consists of a rarefaction wave, a constant state, a stationary discontinuity, a constant state and finally a shock wave. This problem is simulated here on two types of meshes: a first rough mesh consisting of nodes and triangles and a second fine mesh consisting of nodes and triangles. Here again, the results are very satisfactory. We find in Figure 3 the five states of the solution. In addition, these results are in very good agreement with those presented in [5], which further confirms the accuracy of the scheme for dam break simulation with variable porosity.

4. Conclusions

In this work, a finite volume method dedicated to non-homogeneous problems has been extended for the numerical simulation of dam break in free surface flows with variable porosity. The scheme is used on unstructured meshes and preserves the equilibrium property. The two test cases considered here as well as the comparisons with the existing solutions showed the precision of the method. The next step will be to simulate large scale floods involving urbanized areas, considering the shallow water model with porosity.