European Vanilla Option Pricing Model of Fractional Order without Singular Kernel
Abstract
:1. Introduction and Some Preliminaries
2. Description of the Method Using the Caputo–Fabrizio Fractional Operator
3. Solution of the European Option Pricing Problem
3.1. Fractional European Option Pricing Problem in the Sense of the Caputo–Fabrizio Derivative
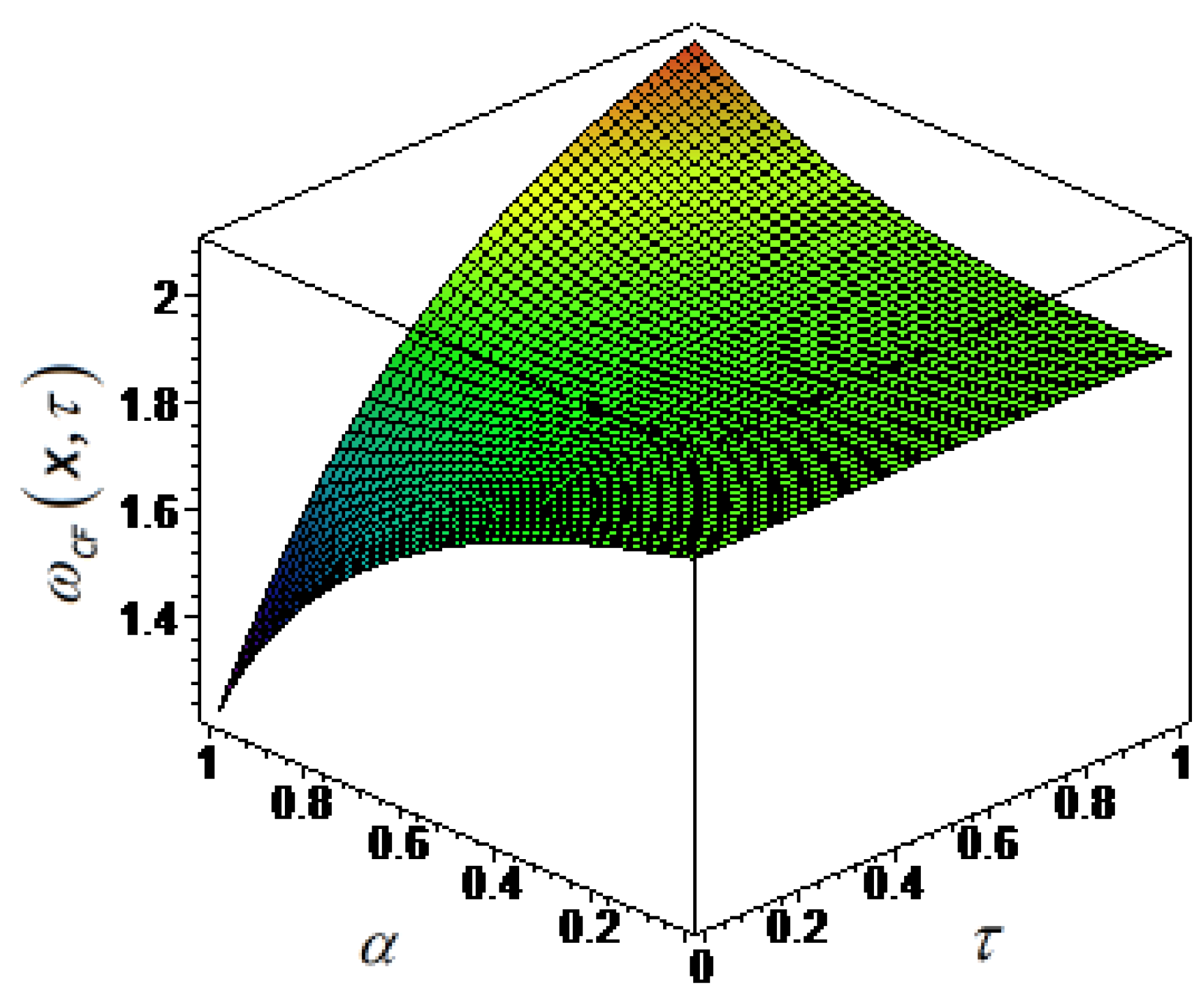
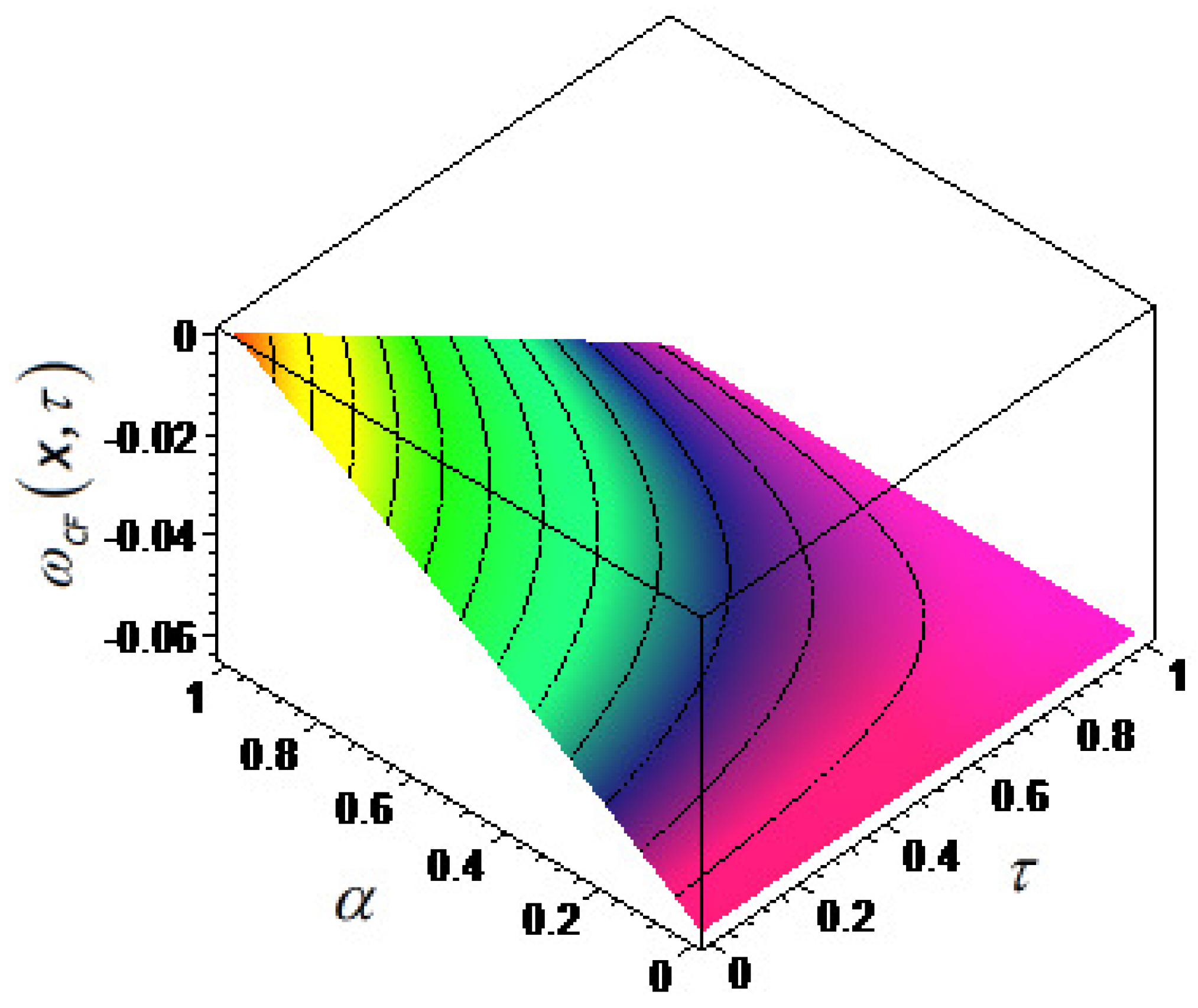
3.2. Fractional Generalized European Option Pricing Problem in the Sense of the Caputo–Fabrizio Derivative
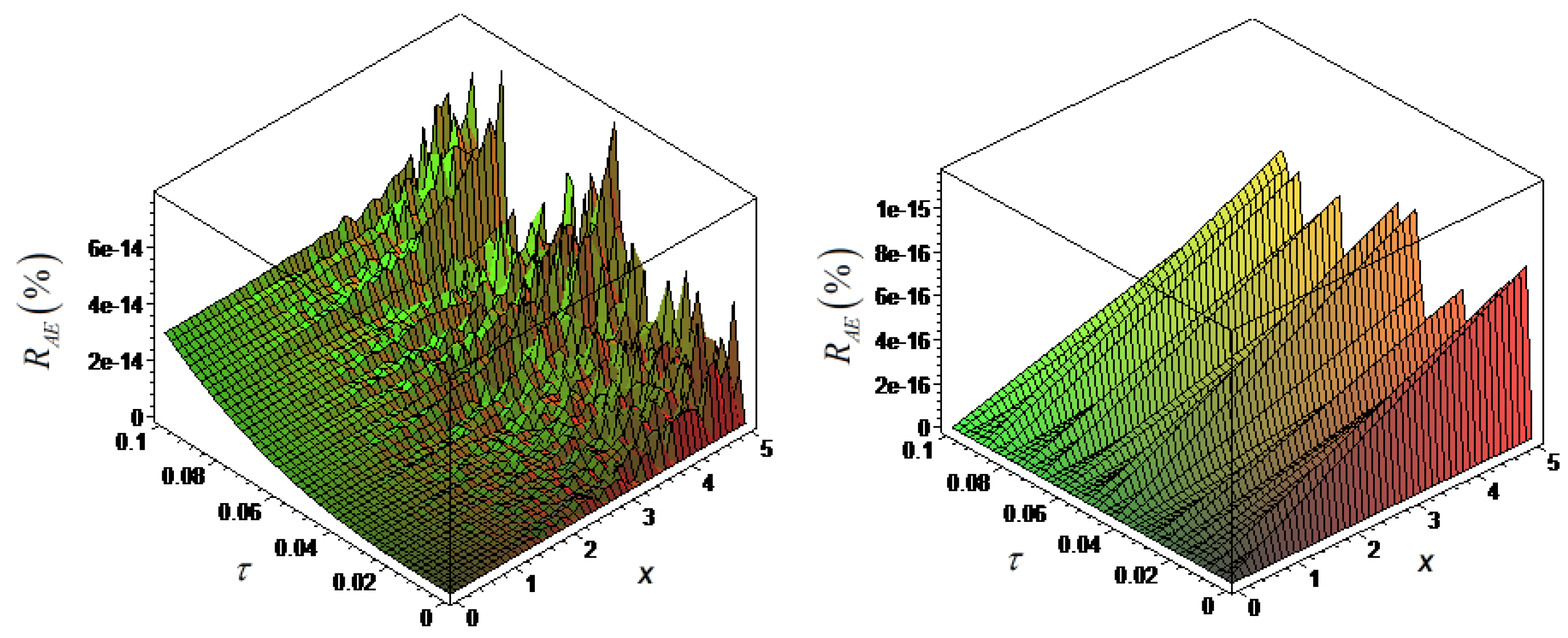
4. Determining Stabilization and Convergence of Suggested Method
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| FDE | Fractional differential equation |
| LHAM | Laplace homotopy analysis method |
| CF | Caputo–Fabrizio |
| AB | Atangana–Baleanu |
| LT | Laplace transform |
| FC | Fractional calculus |
| ENSO | El Niño–Southern Oscillation |
| FBSE | Fractional Black–Scholes equation |
| GFBSE | Generalized fractional Black–Scholes equation |
References
- Gómez-Aguilar, J.F.; Morales-Delgado, V.F.; Taneco-Hernández, M.A.; Baleanu, D.; Escobar-Jiménez, R.F.; Al Qurashi, M.M. Analytical solutions of the electrical RLC circuit via Liouville–Caputo operators with local and non-local kernels. Entropy 2016, 18, 402. [Google Scholar] [CrossRef]
- Özdemir, N.; Yavuz, M. Numerical solution of fractional Black–Scholes equation by using the multivariate Padé approximation. Acta Phys. Pol. A. 2017, 132, 1050–1053. [Google Scholar] [CrossRef]
- Yavuz, M.; Özdemir, N.; Okur, Y.Y. Generalized differential transform method for fractional partial differential equation from finance. In Proceedings of the International Conference on Fractional Differentiation and its Applications, Novi Sad, Serbia, 18–20 July 2016; pp. 778–785. [Google Scholar]
- Alkahtani, B.S.T.; Koca, I.; Atangana, A. Analysis of a new model of H1N1 spread: Model obtained via Mittag-Leffler function. Adv. Mech. Eng. 2017, 9, 1–8. [Google Scholar] [CrossRef]
- Momani, S.; Qaralleh, R. Numerical approximations and Padé approximants for a fractional population growth model. App. Math. Model. 2007, 31, 1907–1914. [Google Scholar] [CrossRef]
- Hashim, I.; Abdulaziz, O.; Momani, S. Homotopy analysis method for fractional IVPs. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 674–684. [Google Scholar] [CrossRef]
- Evirgen, F.; Özdemir, N. Multistage Adomian decomposition method for solving NLP problems over a nonlinear fractional dynamical system. J. Comput. Nonlinear Dyn. 2011, 6. [Google Scholar] [CrossRef]
- Yavuz, M.; Özdemir, N. A quantitative approach to fractional option pricing problems with decomposition series. Konuralp J. Math. 2018, in press. [Google Scholar]
- Elbeleze, A.A.; Kılıçman, A.; Taib, B.M. Homotopy perturbation method for fractional Black–Scholes European option pricing equations using sumudu transform. Math. Prob. Eng. 2013, 2013, 1–7. [Google Scholar] [CrossRef]
- Yavuz, M. Novel solution methods for initial boundary value problems of fractional order with conformable differentiation. Int. J. Opt. Control Theor. Appl. 2018, 8, 1–7. [Google Scholar] [CrossRef]
- Yavuz, M.; Yaşkıran, B. Approximate-analytical solutions of cable equation using conformable fractional operator. New Trends Math. Sci. 2017, 5, 209–219. [Google Scholar] [CrossRef]
- Odibat, Z.; Momani, S.; Erturk, V.S. Generalized differential transform method: Application to differential equations of fractional order. App. Math. Comput. 2008, 197, 467–477. [Google Scholar] [CrossRef]
- Chen, W.; Wang, S. A finite difference method for pricing European and American options under a geometric Lévy process. Management 2015, 11, 241–264. [Google Scholar] [CrossRef]
- Turut, V.; Güzel, N. On solving partial differential equations of fractional order by using the variational iteration method and multivariate Padé approximations. Eur. J. Pure Appl. Math. 2013, 6, 147–171. [Google Scholar]
- Eroğlu, B.İ.; Avcı, D.; Özdemir, N. Optimal control problem for a conformable fractional heat conduction equation. Acta Phys. Pol. A. 2017, 132, 658–662. [Google Scholar] [CrossRef]
- Evirgen, F. Conformable fractional gradient based dynamic system for constrained optimization problem. Acta Phys. Pol. A. 2017, 132, 1066–1069. [Google Scholar] [CrossRef]
- Hu, Y.; Øksendal, B.; Sulem, A. Optimal consumption and portfolio in a Black–Scholes market driven by fractional Brownian motion. Infin. Dimens. Anal. Quantum Prob. Relat. Top. 2003, 6, 519–536. [Google Scholar] [CrossRef]
- Özdemir, N.; Agrawal, O.P.; Karadeniz, D.; Iskender, B.B. Analysis of an axis-symmetric fractional diffusion-wave problem. J. Phys. A Math. Theor. 2009, 42, 355208. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 1–13. [Google Scholar] [CrossRef]
- Atangana, A.; Alkahtani, B.S.T. New model of groundwater flowing within a confine aquifer: Application of Caputo–Fabrizio derivative. Arab. J. Geosci. 2016, 9, 1–8. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Nieto, J.J. Analysis of an El Nino-Southern Oscillation model with a new fractional derivative. Chaos Solitons Fractals 2017, 99, 109–115. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Nieto, J.J. Application of Caputo–Fabrizio derivatives to mhd free convection flow of generalized Walters’-B fluid model. Eur. Phys. J. Plus 2016, 131, 377. [Google Scholar] [CrossRef]
- Morales-Delgado, V.F.; Gómez-Aguilar, J.F.; Yépez-Martínez, H.; Baleanu, D.; Escobar-Jimenez, R.F.; Olivares-Peregrino, V.H. Laplace homotopy analysis method for solving linear partial differential equations using a fractional derivative with and without kernel singular. Adv. Differ. Equ. 2016, 2016, 164. [Google Scholar] [CrossRef]
- Sheikh, N.A.; Ali, F.; Saqib, M.; Khan, I.; Jan, S.A.A.; Alshomrani, A.S.; Alghamdi, M.S. Comparison and analysis of the Atangana–Baleanu and Caputo–Fabrizio fractional derivatives for generalized Casson fluid model with heat generation and chemical reaction. Res. Phys. 2017, 7, 789–800. [Google Scholar] [CrossRef]
- Koca, I.; Atangana, A. Solutions of Cattaneo–Hristov model of elastic heat diffusion with Caputo–Fabrizio and Atangana–Baleanu fractional derivatives. Therm. Sci. 2017, 21, 2299–2305. [Google Scholar] [CrossRef]
- Hristov, J. Steady-state heat conduction in a medium with spatial non-singular fading memory: Derivation of Caputo–Fabrizio space-fractional derivative with Jeffrey’s kernel and analytical solutions. Therm. Sci. 2017, 21, 827–839. [Google Scholar] [CrossRef]
- Alkahtani, B.S.T.; Atangana, A. Controlling the wave movement on the surface of shallow water with the Caputo–Fabrizio derivative with fractional order. Chaos Solitons Fractals 2016, 89, 539–546. [Google Scholar] [CrossRef]
- Alkahtani, B.S.T.; Atangana, A. Analysis of non-homogeneous heat model with new trend of derivative with fractional order. Chaos Solitons Fractals 2016, 89, 566–571. [Google Scholar] [CrossRef]
- Hristov, J. Transient heat diffusion with a non-singular fading memory: From the Cattaneo constitutive equation with Jeffrey’s kernel to the Caputo–Fabrizio time-fractional derivative. Therm. Sci. 2016, 20, 757–762. [Google Scholar] [CrossRef]
- Atangana, A.; Koca, I. On the new fractional derivative and application to nonlinear Baggs and Freedman model. J. Nonlinear Sci. Appl. 2016, 9, 2467–2480. [Google Scholar]
- Ghandehari, M.A.M.; Ranjbar, M. European option pricing of fractional Black–Scholes model with new Lagrange multipliers. Comput. Methods Differ. Equ. 2014, 2, 1–10. [Google Scholar]
- Yerlikaya-Özkurt, F.; Vardar-Acar, C.; Yolcu-Okur, Y.; Weber, G.W. Estimation of the Hurst parameter for fractional Brownian motion using the CMARS method. J. Comput. Appl. Math. 2014, 259, 843–850. [Google Scholar] [CrossRef]
- Black, F.; Scholes, M. The pricing of options and corporate liabilities. J. Political Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef]
- Wilmott, P.; Howison, S.; Dewynne, J. The Mathematics of Financial Derivatives: A Student Introduction; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Ahmed, E.; Abdusalam, H.A. On modified Black–Scholes equation. Chaos Solitons Fractals 2004, 22, 583–587. [Google Scholar] [CrossRef]
- Cen, Z.; Le, A. A robust and accurate finite difference method for a generalized Black–Scholes equation. J. Comput. Appl. Math. 2011, 235, 3728–3733. [Google Scholar] [CrossRef]
- Meng, L.; Wang, M. Comparison of Black–Scholes formula with fractional Black–Scholes formula in the foreign exchange option market with changing volatility. Asia-Pac. Finan Markets 2010, 17, 99–111. [Google Scholar] [CrossRef]
- Yavuz, M.; Özdemir, N. A different approach to the European option pricing model with new fractional operator. Math. Model. Nat. Phenom. 2018, in press. [Google Scholar] [CrossRef]
- Madani, M.; Fathizadeh, M.; Khan, Y.; Yildirim, A. On the coupling of the homotopy perturbation method and Laplace transformation. Math. Comput. Model. 2011, 53, 1937–1945. [Google Scholar] [CrossRef]



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yavuz, M.; Özdemir, N. European Vanilla Option Pricing Model of Fractional Order without Singular Kernel. Fractal Fract. 2018, 2, 3. https://doi.org/10.3390/fractalfract2010003
Yavuz M, Özdemir N. European Vanilla Option Pricing Model of Fractional Order without Singular Kernel. Fractal and Fractional. 2018; 2(1):3. https://doi.org/10.3390/fractalfract2010003
Chicago/Turabian StyleYavuz, Mehmet, and Necati Özdemir. 2018. "European Vanilla Option Pricing Model of Fractional Order without Singular Kernel" Fractal and Fractional 2, no. 1: 3. https://doi.org/10.3390/fractalfract2010003