Modeling, Simulation and Control of the Walking of Biped Robotic Devices, Part II: Rectilinear Walking
Abstract
:1. Introduction
- An inner one, embedding admittance control in a position loop, which closes a feedback from exoskeleton joint positions and velocities. This is solved by the linearization of the model of the exoskeleton and patient joined together. A two degrees of freedom approach is adopted using ∞ multivariable robust control theory. The exoskeleton is compliant with the patient’s efforts in the neighborhood of given joint angle reference positions, and this is according to an imposed admittance driven by the patient’s EMG signals.
- An outer control loop, closing a feedback from measurements performed on the feet-sole center of pressure (CoP) (i.e., zero moment point (ZMP)), corrects the joint angle reference positions in the inner loop, in order to maintain postural equilibrium.
1.1. State of the Art of Bipedal Gait Control
1.2. Gait Control
- Modeling a multi-body dynamical system switching periodically between the two phases of gait: single and double stance. The dynamical behavior of the multi-body system driven by joint torques and ground reaction forces/torques is given by a system of second order non-linear differential equations, referred to as hybrid complementarity dynamical systems (see, for example, [19] Chapter 16, Section 3). This mechanical system is subject to changing unilateral constraints represented by the contact of the soles of the supporting foot/feet with the ground. The resulting reactions forces/torques are important for balancing the weight and postural control, as they define the ZMP, i.e., the CoP under the soles of the feet, which is the primary measure and objective of postural equilibrium.
- Implementing gait so that nominal (open loop) trajectories of the projection of the center of gravity (COG) on the ground (and consequently, trajectories of the joint angles) satisfy, at each instant of time, precise ZMP constraints to maintain equilibrium during a dynamic walking. This requires a certain degree of motion anticipation.
- Designing a switching feedback control to offer acceptable gait trajectories under uncertainty. This means managing compliance with the swing foot when entering in double stance and for transferring weight load.
- Transferring reference trajectories (defined in terms of positions, velocities, constraint reaction forces and torques) from the Cartesian space to the joint space for closed loop motion control. This involves inverse kinematics in a highly non-linear dynamical environment, in the presence of singularities.
2. Controlling Gait
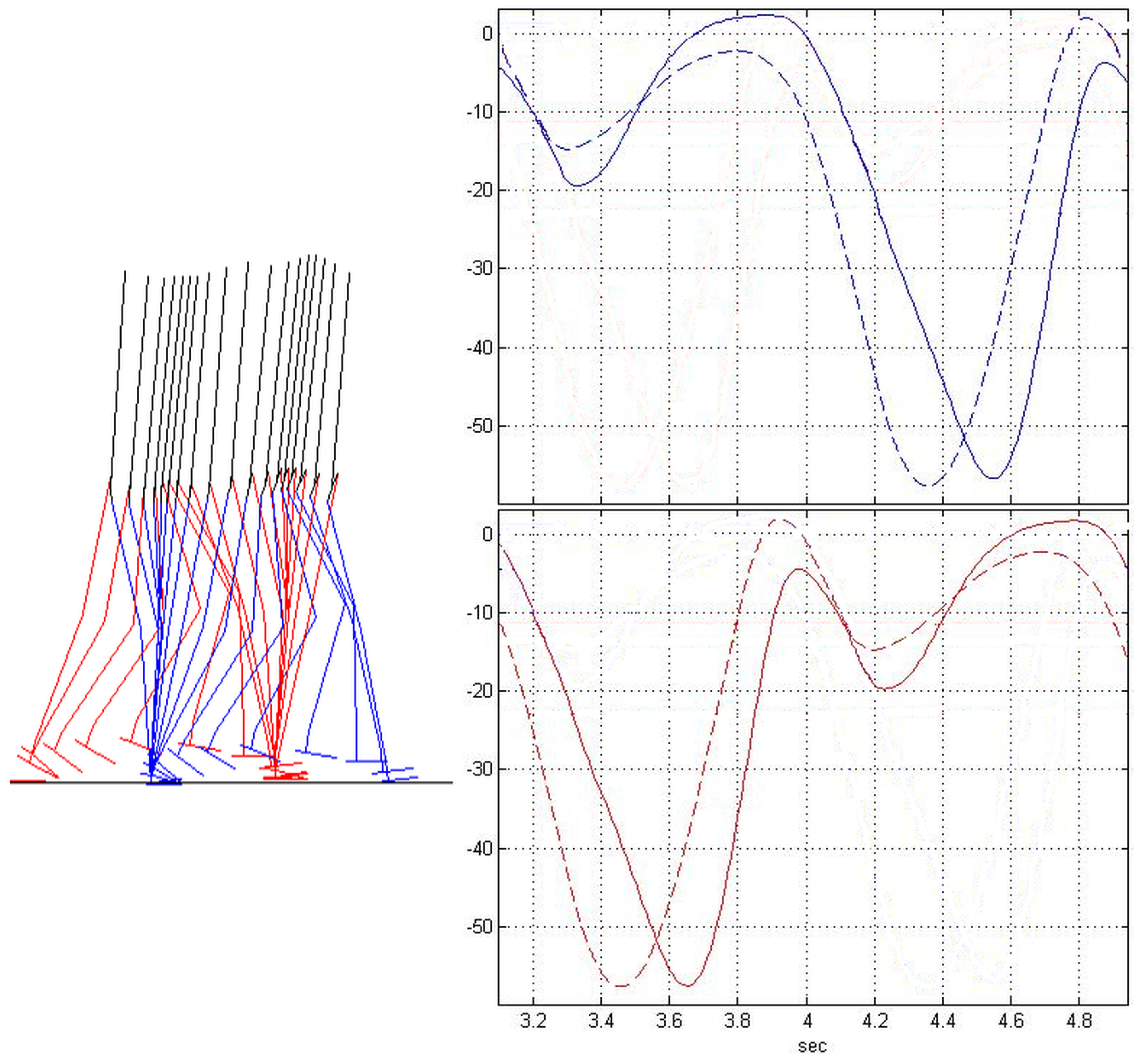
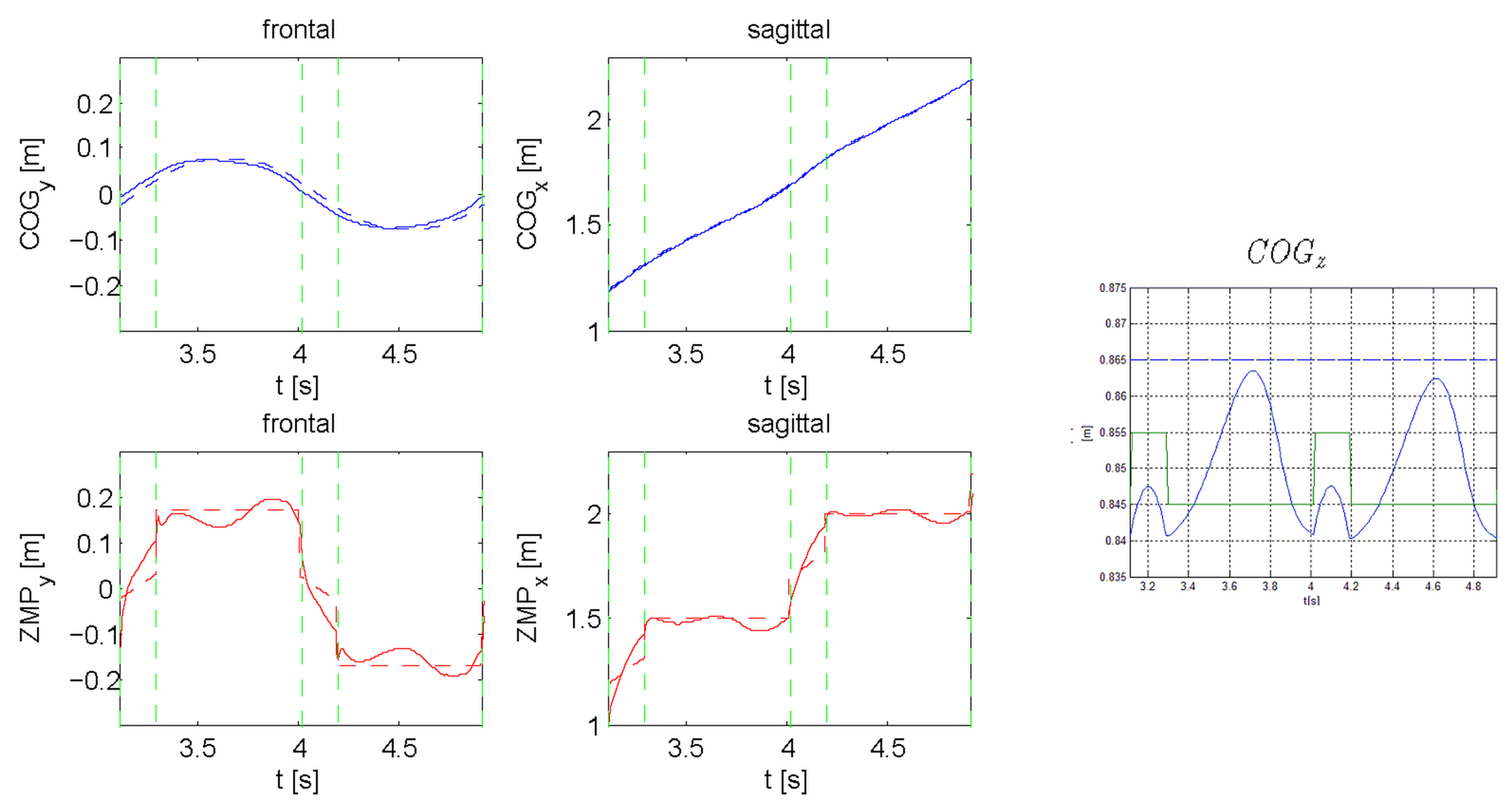
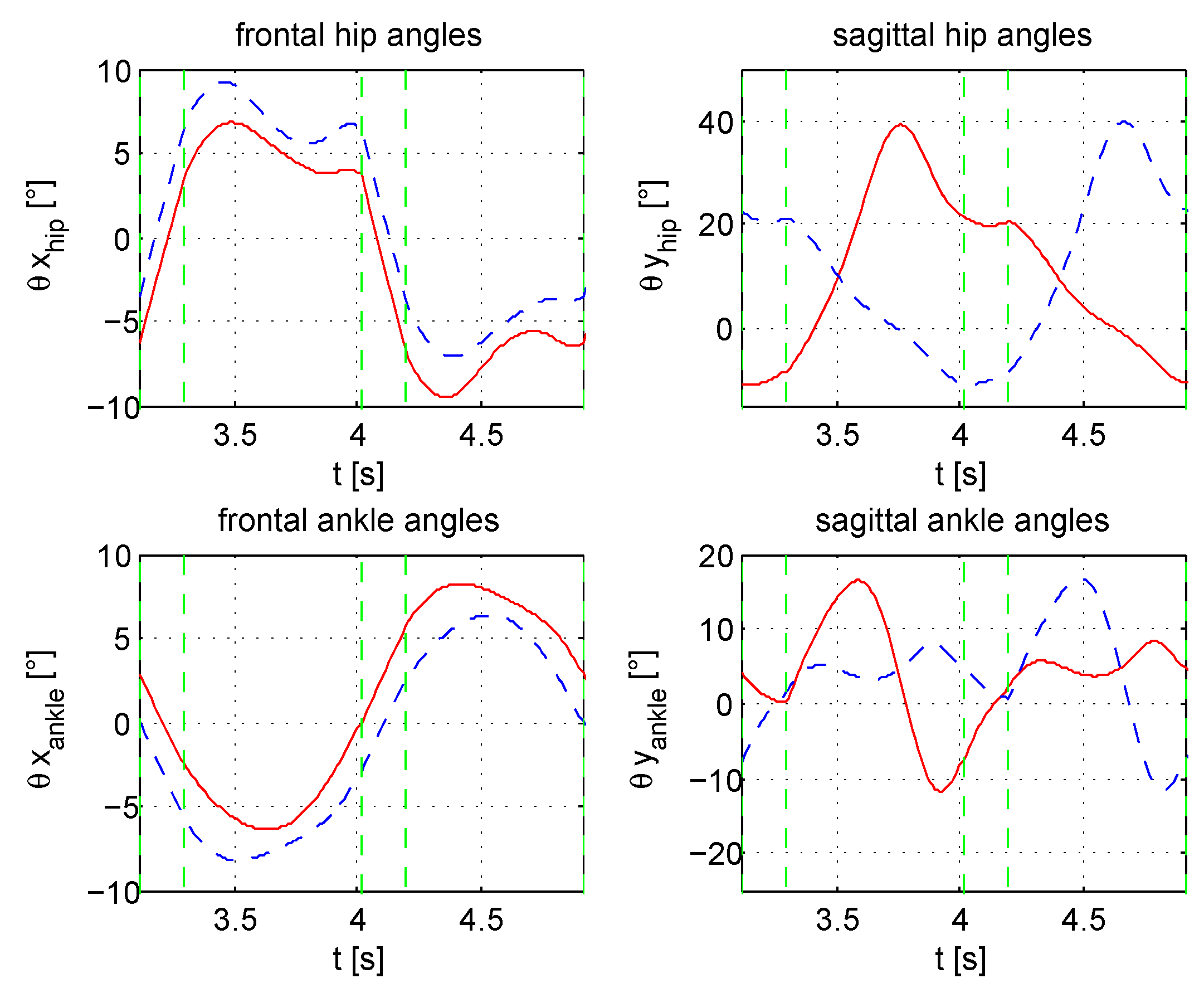
2.1. Equilibrium, Posture and Preview Signals
2.2. The Jacobian Matrices
The Extended Jacobian
- It copes with the occasional singularity of the standard Jacobian matrices, which occurs when the knees are fully stretched during gait.
- It copes with possible kinematical inconsistencies between knee angles, the vertical coordinate of the COG and swinging foot coordinates arising in the real-time synthesis. These inconsistencies are due to approximate modeling and simplified reference functions.
- It allows the patient’s walking style to be embedded in the control of the exoskeleton by explicitly assigning the trajectories of the knee joint velocities, when interacting with the patient through compliance.
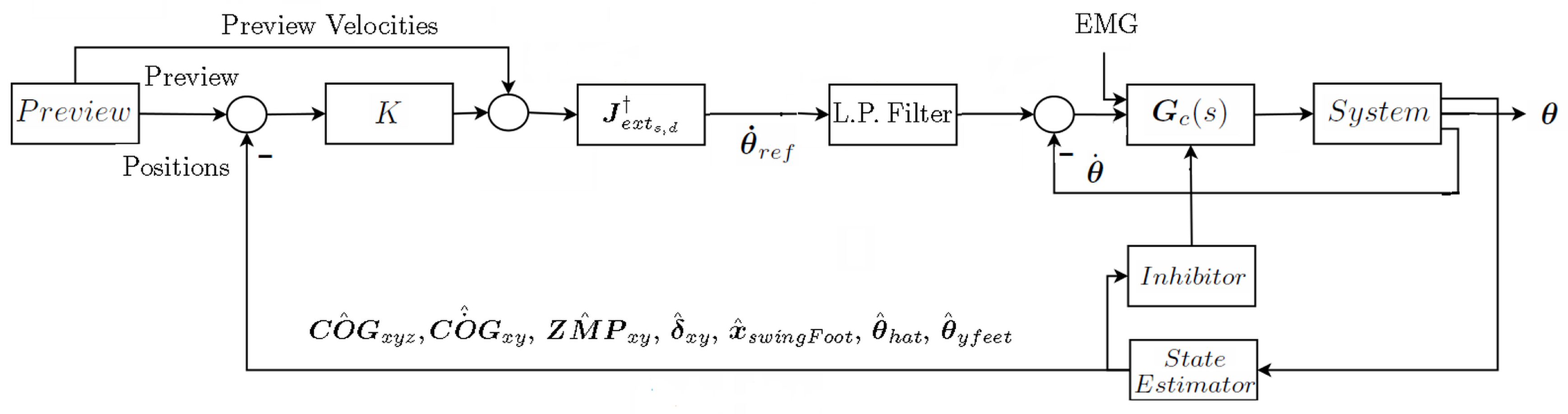
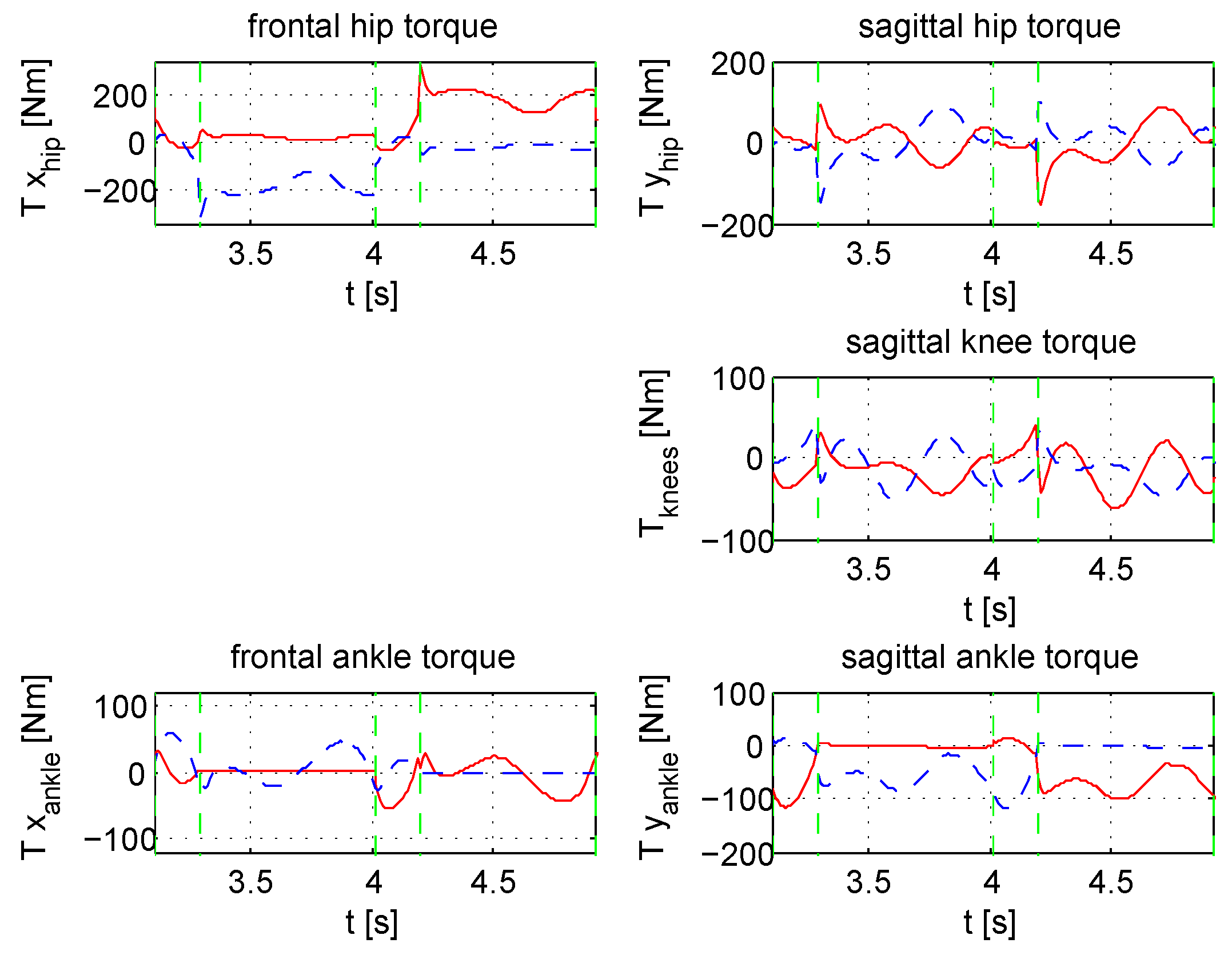
2.3. Closing the Loop
- is the pseudoinverse of the extended Jacobian matrix , as described in Section 2.2;
- Vi is the vector of the preview velocities and acts as feed-forward;
- Es is a vector containing the feedback tracking errors, computed as the difference between the preview/reference and the estimates of the corresponding Cartesian variables.
2.3.1. Knee References
2.3.2. Filtering or Integrating
2.3.3. Further Comments on the Extended Jacobian Matrix
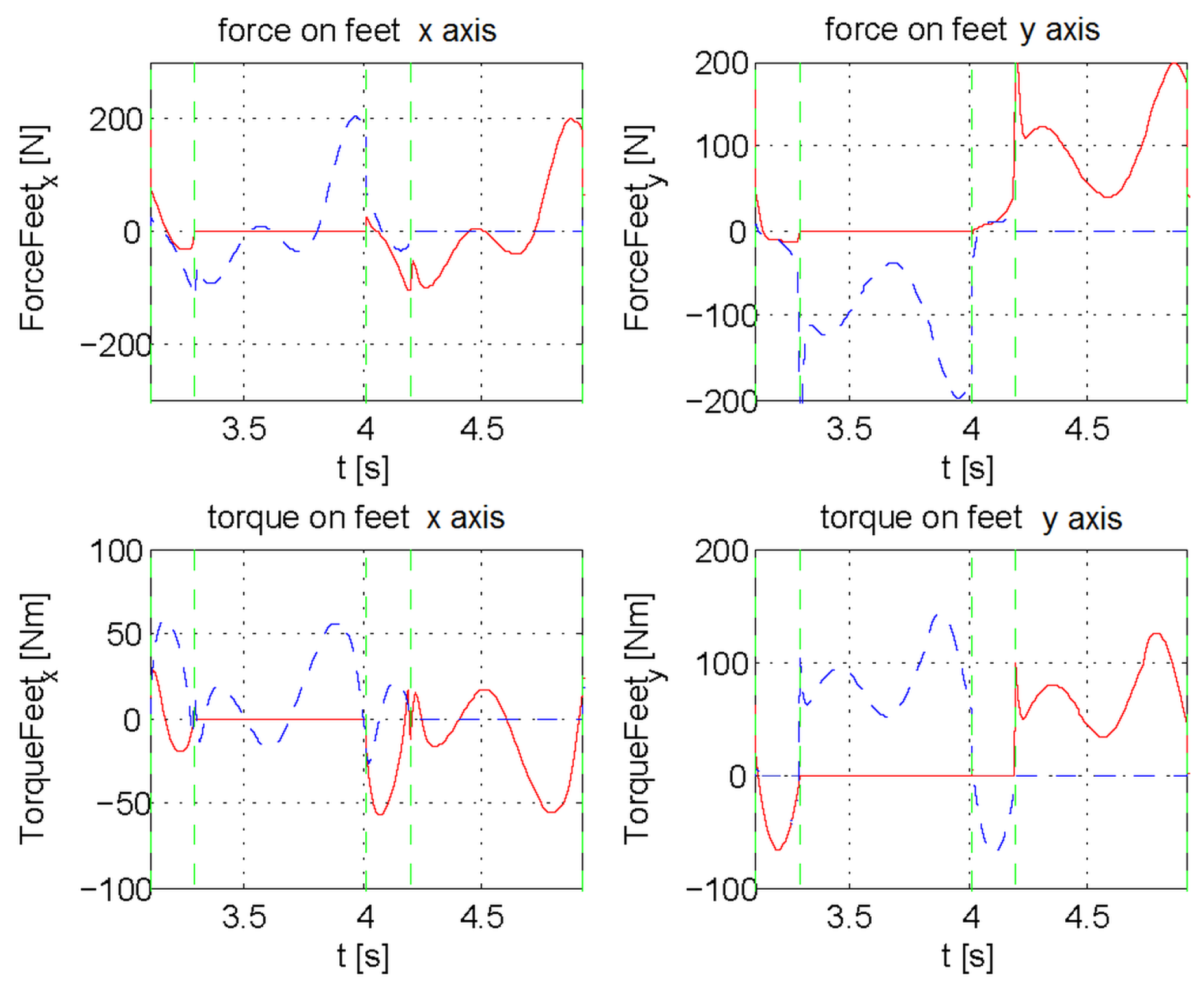
3. Reaction Force Control of the Feet
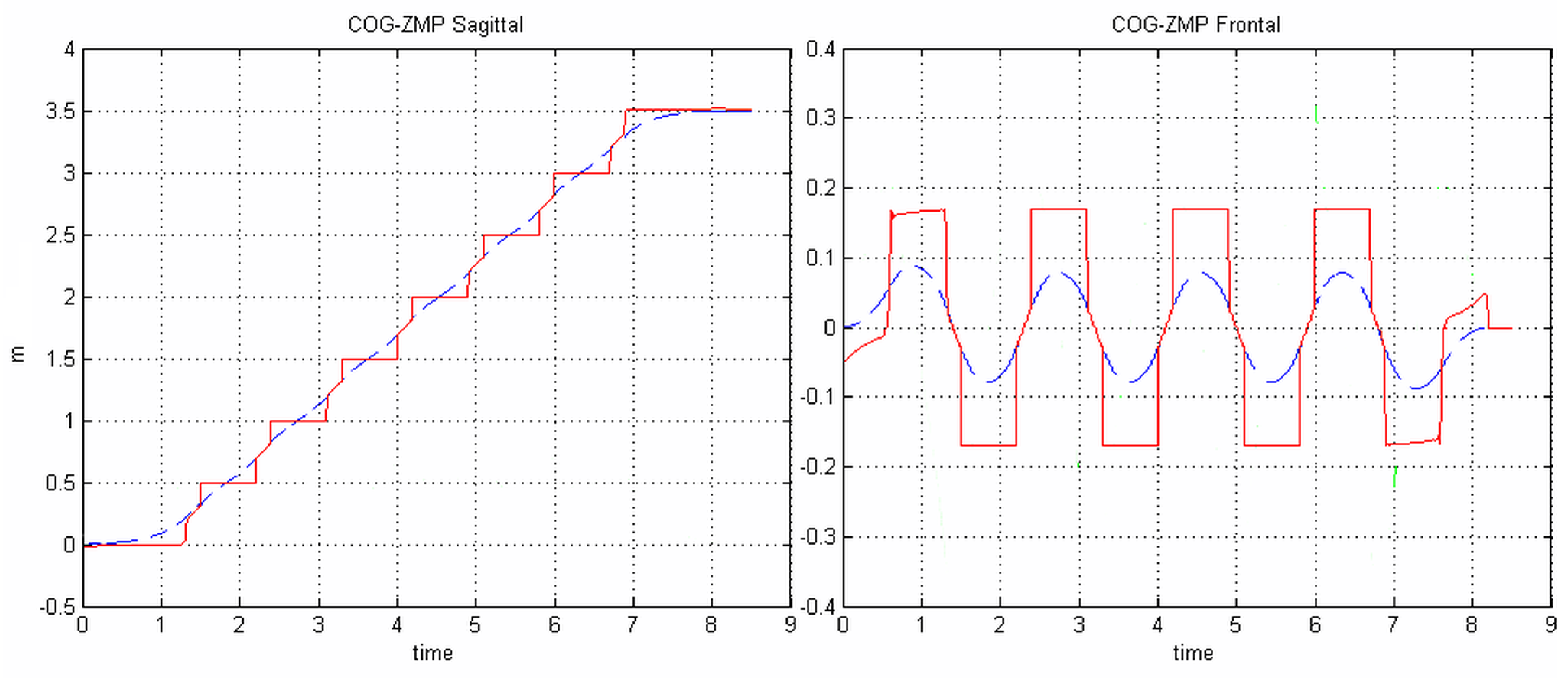
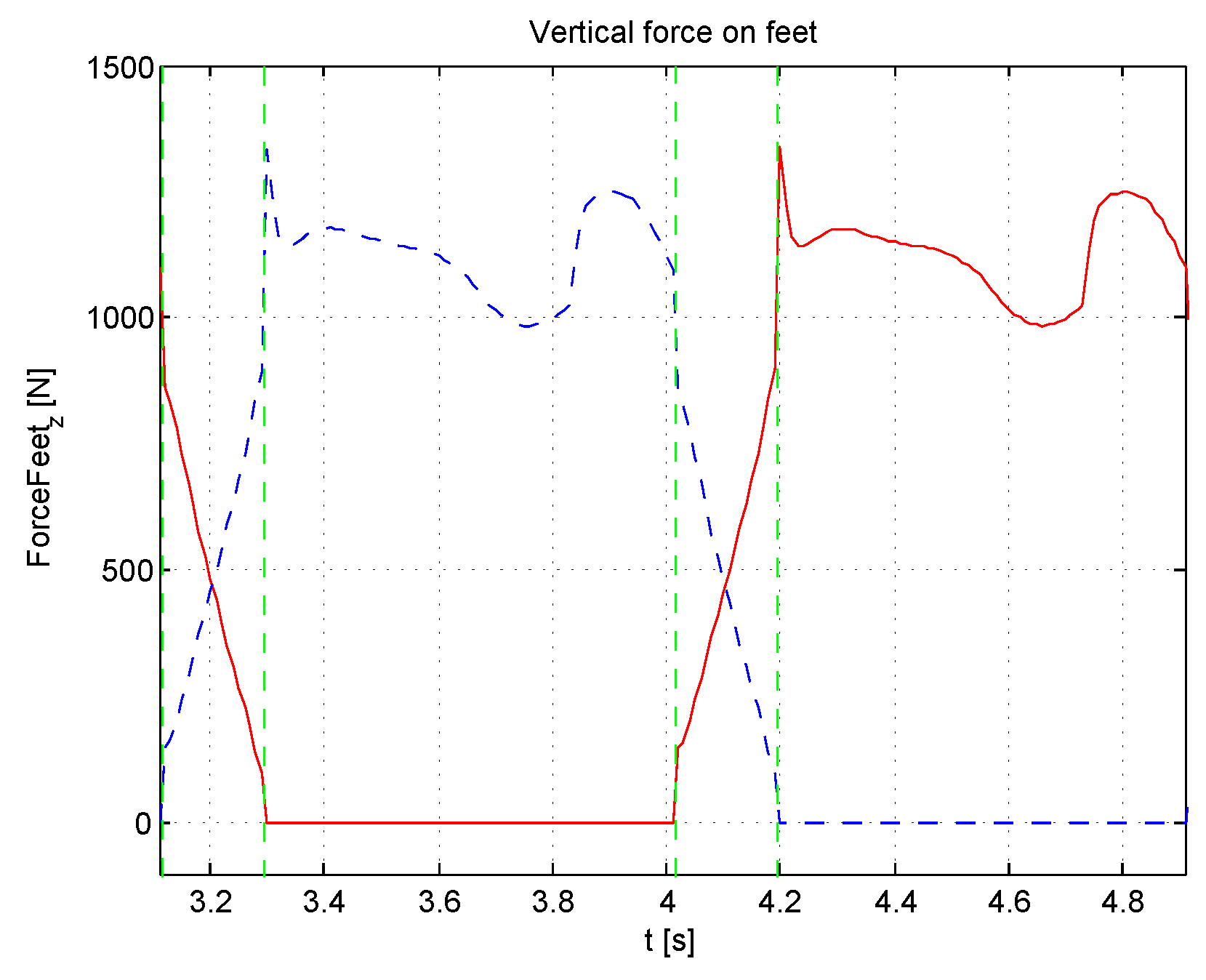
3.1. Balancing Weight
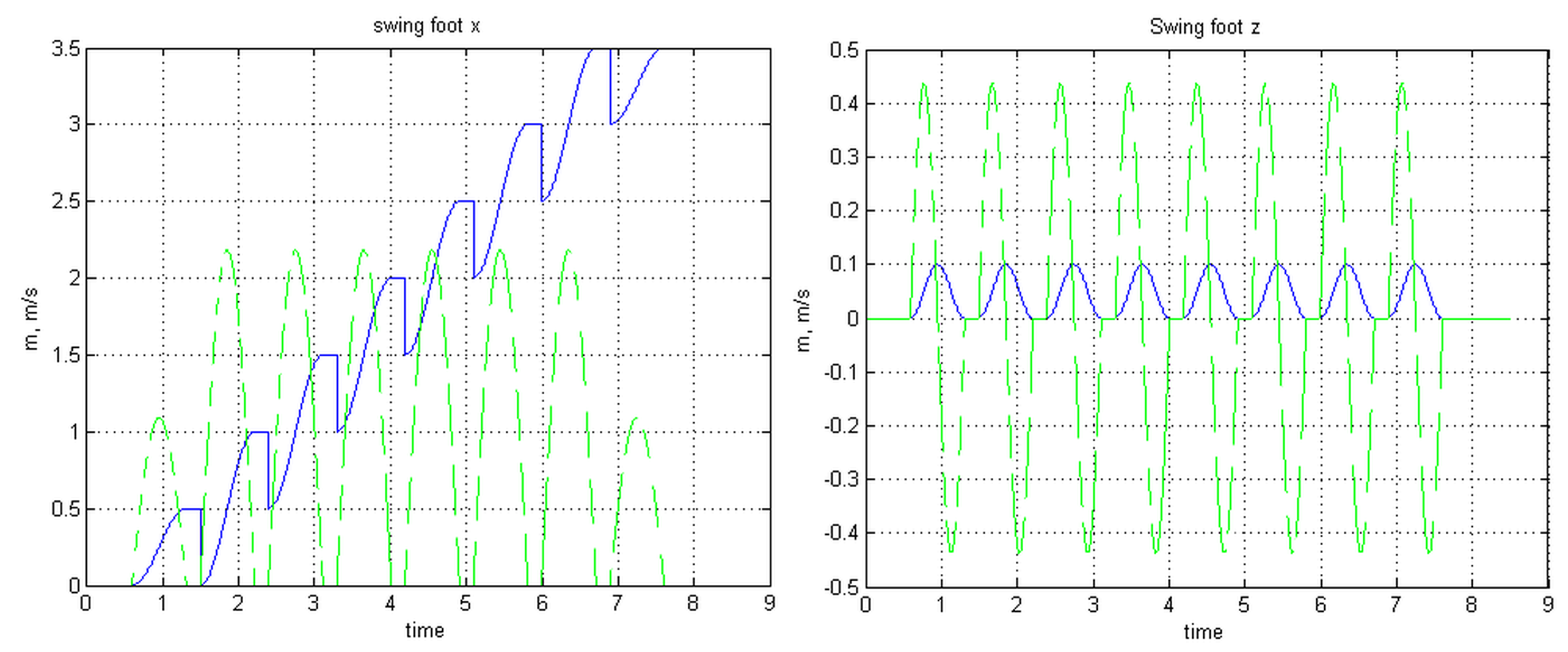
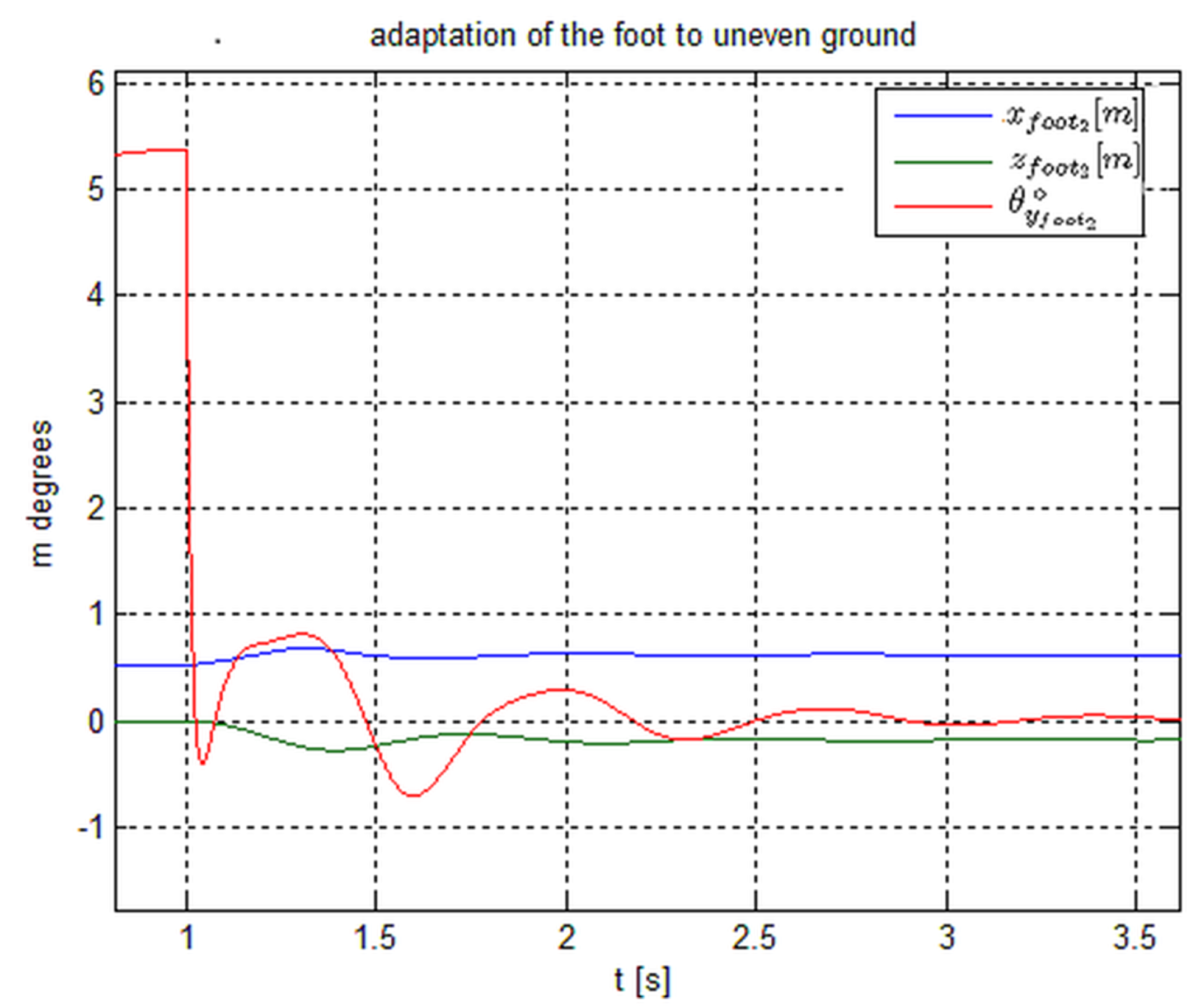
3.2. Adapting the Swing Foot on Uneven Ground at the End of a Single Stance
- the switching of the control from single to double stance is anticipated with respect to the event Heel2 strike of an interval of time compatible with the time response of the joint actuators.
- The small adjustments of the swing foot in the instants just before and after the contact, during the adaptation, are ignored by the postural control, which treats them as disturbances.
- A virtual force/torque is imagined as being applied to the swing foot (still flying) with a desired spring admittance () attracting the foot toward the real future contact position and soil attitude that have just been measured. They may have slightly different values than those of the reference trajectory planned in advance.
- The reaction force control for is activated, acting on Taux with a scheme similar to Equation (14), driven by the virtual force/torque before the contact, and then, after the contact by the real ones, with the objective to home to the contact point and adapting the foot to the ground by bringing reaction forces/torques to a minimum.
4. The Case Study
5. Conclusions
- to resolve the singularity in the inverse kinematics and allow the knees to be fully stretched, by introducing fake knee joint trajectories;
- to accommodate kinematics inconsistency due to model and preview trajectories’ approximations;
- to take into account the actions and style of the wearer, in the case of an exoskeleton with a partially able patient, ending up in a hybrid control system.
Acknowledgments
Author Contributions
Conflicts of Interest
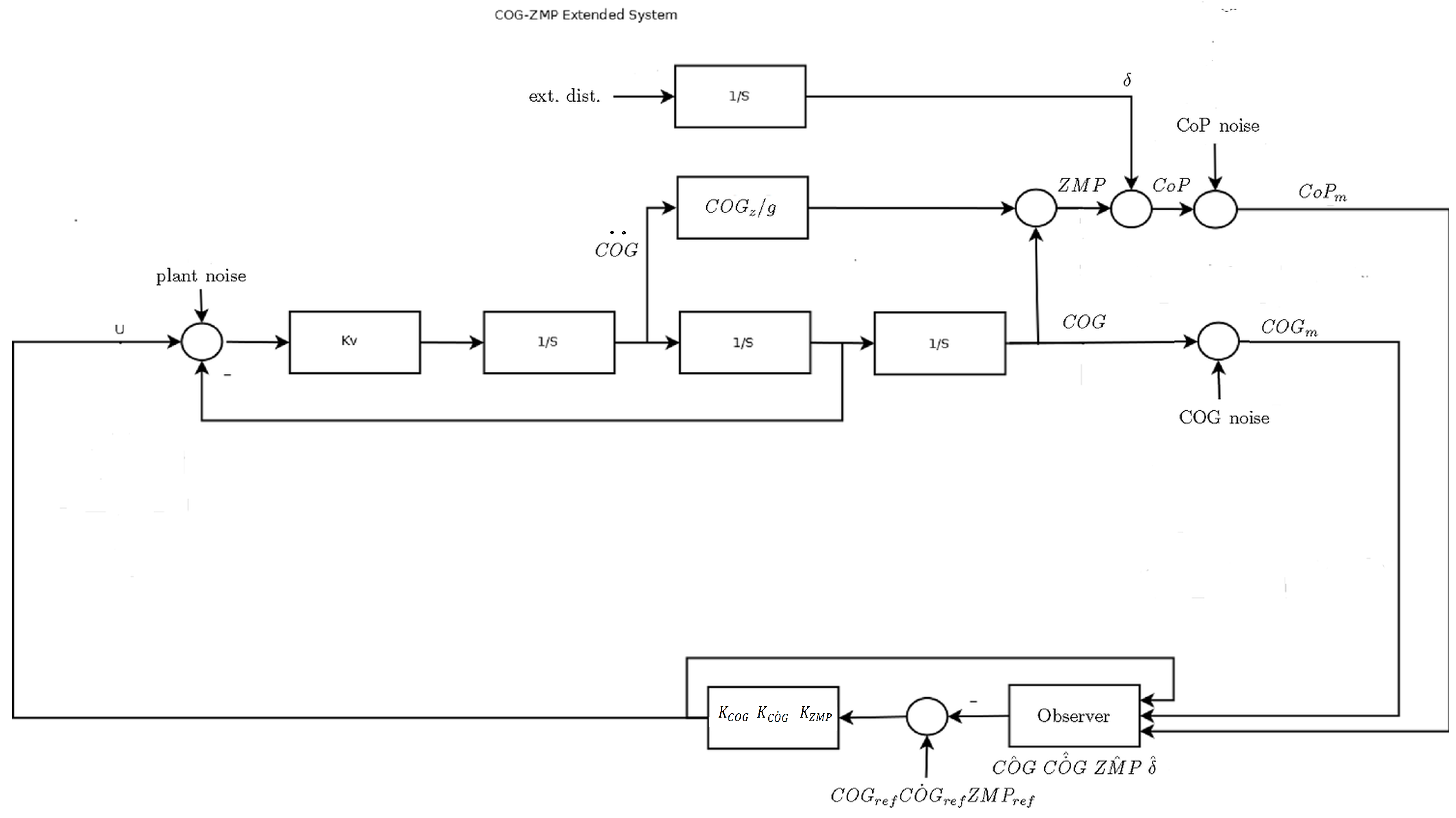
Appendix A. COG/ZMP Estimator and Control
- As the weight distribution is seldom well known, especially in the case of an exoskeleton, an a priori calibration of the kinematics, with static and dynamic experiments, is suggested, adopting the same feet sensors that will be used for the control.
- An extended estimator is introduced by adding in its simplest form one more state to the original model, to take into account the disturbances.
References
- Menga, G.; Ghirardi, M. Lower Limb Exoskeleton with postural equilibrium enhancement for rehabilitation purposes. Internal Report DAUIN—Politecnico di Torino. Available online: https://dl.dropboxusercontent.com/u/26129003/SUBM1.pdf (accessed on 17 March 2016).
- Hirai, K.; Hirose, M.; Haikawa, Y.; Takenaka, T. The development of honda humanoid robot. In Proceedings of the 1998 IEEE International Conference on Robotics and Automation, Leuven, Belgium, 16–20 May 1998.
- Sakagami, Y.; Watanabe, R.; Aoyama, C.; Matsunaga, S.; Higaki, N.; Fujimura, K. The intelligent ASIMO: System overview and integration. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Lausanne Switzerland, October 2002; pp. 2478–2483.
- Endo, G.; Nakanishi, J.; Morimoto, J.; Cheng, G. Experimental studies of a neural oscillator for biped Locomotion with QRIO. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcellona, Spain, 18–22 April 2005.
- Lohmeier, S.; Loffler, K.; Gienger, M.; Ulbrich, H.; Pfeiffer, F. Computer system and control of biped “Johnnie”. In Proceedings of the 2004 IEEE International Conference on Robotics and Automation, New Orleans, USA, 26 April–1 May 2004; pp. 4222–4227.
- Yokoi, K.; Kanehiro, F.; Kaneko, K.; Kajita, S.; Fujiwara, K.; Hirukawa, H. Experimental study of humanoid robot HRP-1S. Int. J. Robot. Res. 2004, 23, 351–362. [Google Scholar] [CrossRef]
- Park, I.W.; Kim, J.Y.; Lee, J.; Oh, J.H. Online free walking trajectory generation for biped humanoid robot HR-3(HUBO). In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–19 May 2006.
- Sentis, L.; Khatib, O. Synthesis of whole-body behaviors through hierarchical control of behavioral primitives. Int. J. Humanoid Robot. 2005, 2, 505–518. [Google Scholar] [CrossRef]
- Choi, Y.; Kim, D.; Oh, Y.; You, B. Posture/walking control for humanoid robot based on kinematic resolution of CoM jacobian with embedded motion. IEEE Trans. Robot. 2007, 22, 1285–1293. [Google Scholar] [CrossRef]
- Sentis, L.; Park, J.; Khatib, O. Compliant control of multicontact and center-of-mass behaviors in humanoid robots. IEEE Trans. Robot. 2010, 26, 483–501. [Google Scholar] [CrossRef]
- Azevedo, C.; Poignet, P. Artificial locomotion control: From human to robots. Robot. Auton. Syst. 2004, 47, 203–223. [Google Scholar] [CrossRef]
- Vukobratovic, M. Humanoids robots: Past, present state, future. In Proceedings of the SISY—Serbian-Hungarian Joint Symposium on Intelligent Systems, Subotica, Serbia, 29–30 September 2006.
- Katayama, T.; Ohki, T.; Inoue, T.; Kato, T. Design of an optimal controller for a discrete time system subject to previewable demand. Int. J. Control 1985, 41, 677–699. [Google Scholar] [CrossRef]
- Yang, W.; Chong, N.Y.; Ra, S.; Kim, C.; You, B.J. Self-stabilizing bipedal locomotion employing neural oscillators. In Proceedings of the 2008 8th IEEE-RAS International Conference on Humanoid Robots, Daejeon, Korea, 1–3 December 2008.
- Righetti, L.; Ijspeert, A. Programmable central pattern generators: An application to biped locomotion control. In Proceedings of the IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–19 May 2006.
- Kajita, S.; Espiau, B. Legged Robots; Springer Handbook of Robotics; Springer Berlin Heidelberg: Heidelberg, Germany, 2008; pp. 361–389. [Google Scholar]
- Hurmuzlu, Y.; Genot, F.; Brogliato, B. Modeling, stability and control of biped robots-a general framework. Automatica 2004, 40, 1647–1664. [Google Scholar] [CrossRef]
- Azevedo, C.; Espiau, B.; Amblard, B.; Assaiante, C. Bipedal locomotion; toward a unified concept in robotics and neuroscience. Biol. Cybern. 2007, 96, 209–228. [Google Scholar] [CrossRef] [PubMed]
- Siciliano, B.; Khatib, O. Springer Handbook of Robotics; Springer: Berlin, Germany; Heidelberg, Germany, 2008; Chapter 16. [Google Scholar]
- Kane, T.R.; Levinson, D.A. Dynamics: Theory and Applications; McGraw-Hill: New York, NY, USA, 1985. [Google Scholar]
- Kajita, S.; Kanehiro, F.; Kaneko, K.; Fujiwara, K.; Harada, K.; Yokoi, K.; Hirukawa, H. Biped walking pattern generation by using preview control of zero-moment point. In Proceedings of the 2003 IEEE International Conference on Robotics and Automation, Taipei, Taiwan, 14–19 September 2003.
- Yamane, K.; Nakamura, Y. Natural motion animation through constraining and deconstraining at will. IEEE Trans. Vis. Comput. Graph. 2003, 9, 352–360. [Google Scholar] [CrossRef]
- Saunders, J.B.; Inman, V.T.; Eberhardt, D.H. The major determinants in normal and pathological gait. J. Bone Joint Surg. 1953, 35-A, 543–558. [Google Scholar] [PubMed]
- Ortega, J.; Farley, C.T. Minimizing center of mass vertical movement increases metabolic cost in walking. J. Appl. Physiol. 2005, 99, 2099–2107. [Google Scholar] [CrossRef] [PubMed]
- Srinivasan, M.; Ruina, A. Idealized walking and running gaits minimize work. Proc. R. Soc. A 2007, 463, 2429–2446. [Google Scholar] [CrossRef]
- Kuo, A. The six determinants of gait and the inverted pendulum analogy: A dynamic walking perspective. Hum. Mov. Sci. 2007, 26, 617–56. [Google Scholar] [CrossRef] [PubMed]
- Menga, G.; Ghirardi, M. Modeling, Simulation and Control of the Walking of Biped Robotic Devices—Part I: Modeling and Simulation using Autolev. Inventions 2016, 1, 6. [Google Scholar]
- Patton, J. Normal Gait Part of Kinesiology. 2002. Available online: http://www.smpp.northwestern.edu/~jim/kinesiology/partA_introGait.ppt.pdf (accessed on 17 March 2016).
- Patton, J. Gait Section, Part B, Kinesiology. Available online: http://www.smpp.northwestern.edu/~jim/kinesiology/partB_GaitMechanics.ppt.pdf (accessed on 17 March 2016).
- Menga, G.; Ghirardi, M. Estimation and Closed Loop Control of COG/ZMP in Biped Devices Blending CoP Measures and Kinematic Information. Internal Report DAUIN—Politecnico di Torino. Available online: https://dl.dropboxusercontent.com/u/26129003/COGZMP.pdf (accessed on 17 March 2016).


© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Menga, G.; Ghirardi, M. Modeling, Simulation and Control of the Walking of Biped Robotic Devices, Part II: Rectilinear Walking. Inventions 2016, 1, 7. https://doi.org/10.3390/inventions1010007
Menga G, Ghirardi M. Modeling, Simulation and Control of the Walking of Biped Robotic Devices, Part II: Rectilinear Walking. Inventions. 2016; 1(1):7. https://doi.org/10.3390/inventions1010007
Chicago/Turabian StyleMenga, Giuseppe, and Marco Ghirardi. 2016. "Modeling, Simulation and Control of the Walking of Biped Robotic Devices, Part II: Rectilinear Walking" Inventions 1, no. 1: 7. https://doi.org/10.3390/inventions1010007





