Marine Predator Algorithm-Based Optimal PI Controllers for LVRT Capability Enhancement of Grid-Connected PV Systems
Abstract
:1. Introduction
1.1. General Overview of PV Grid-Connected Systems
1.2. Incitement and Motivation
1.3. Literature Review and Research Gaps
1.4. Contribution and Paper Organization
2. Materials and Methods
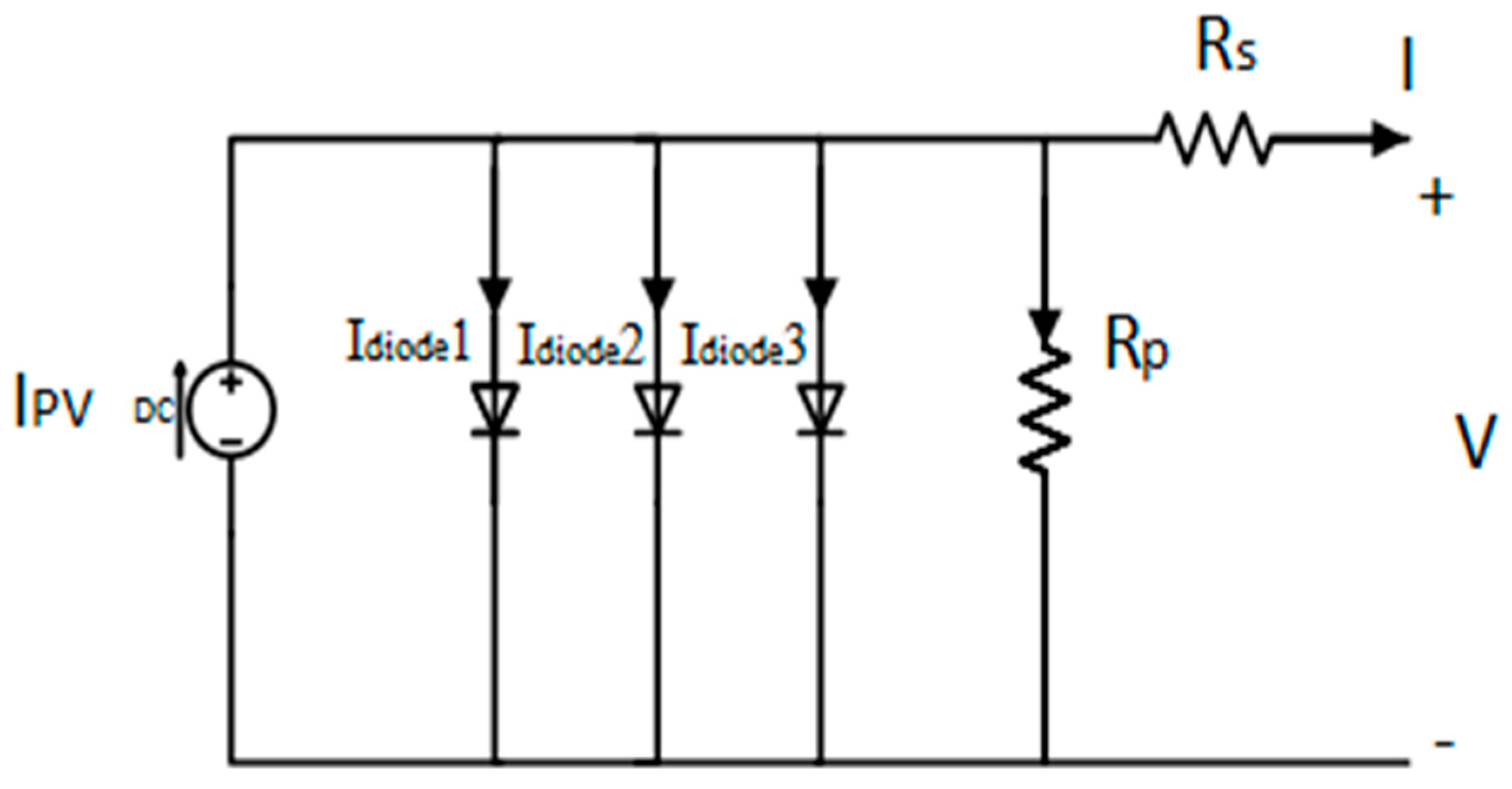
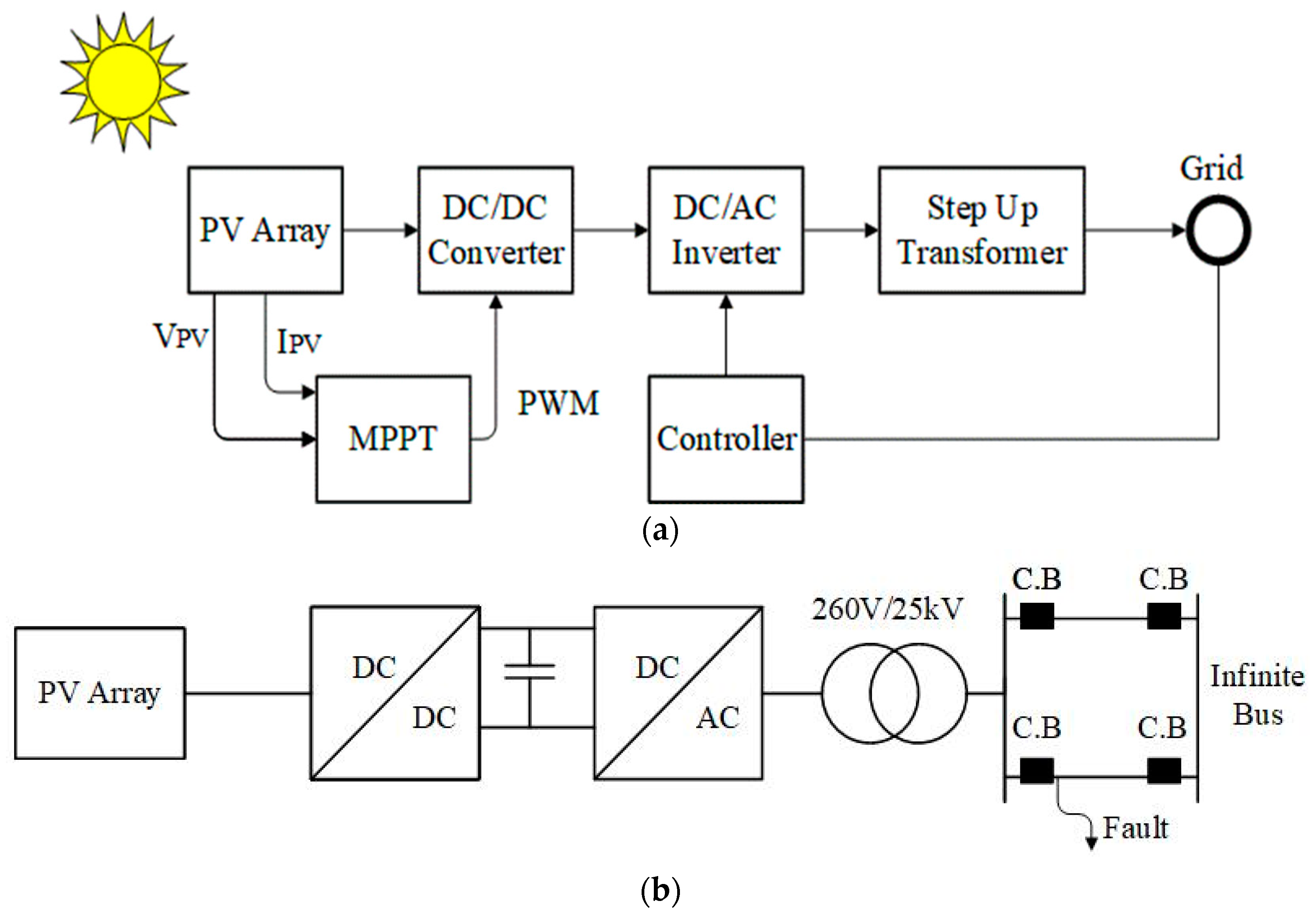
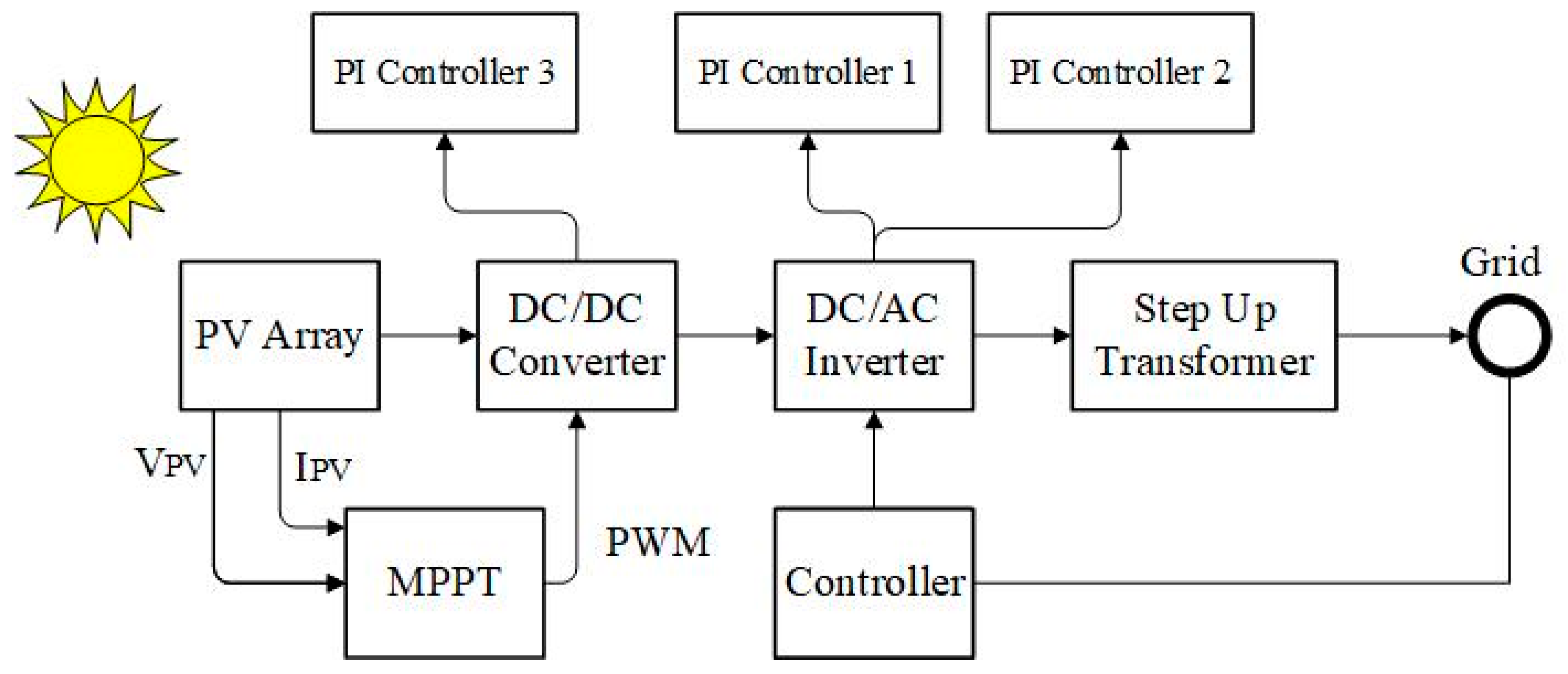
2.1. System Modelling
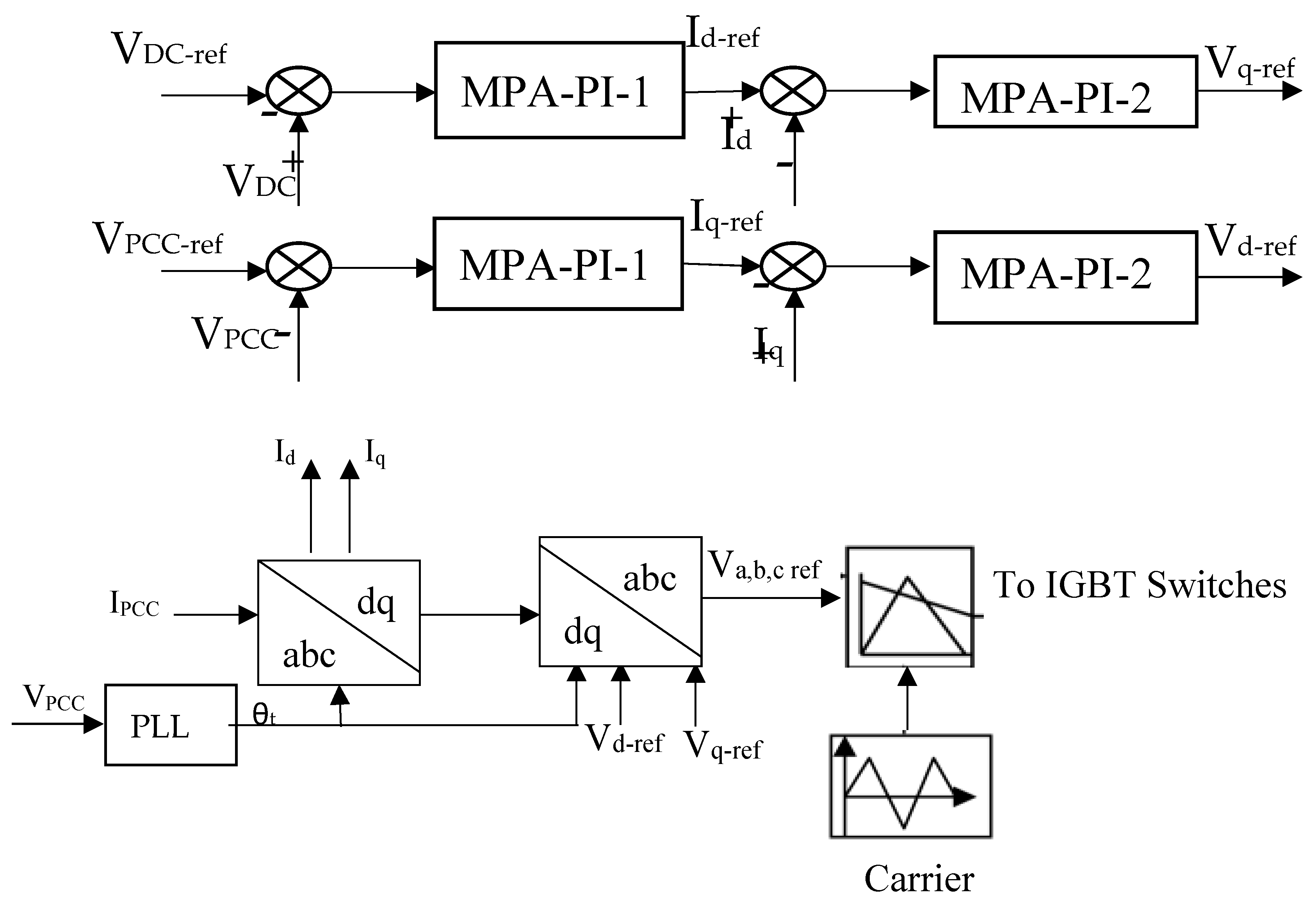
2.2. Control Strategy of the System
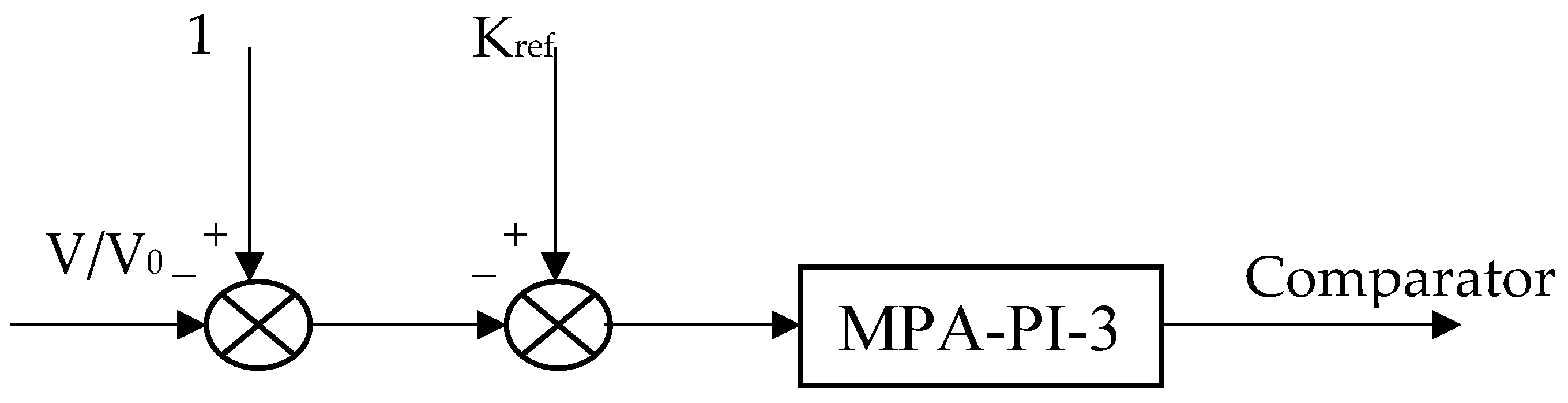
2.2.1. DC–DC Boost Converter
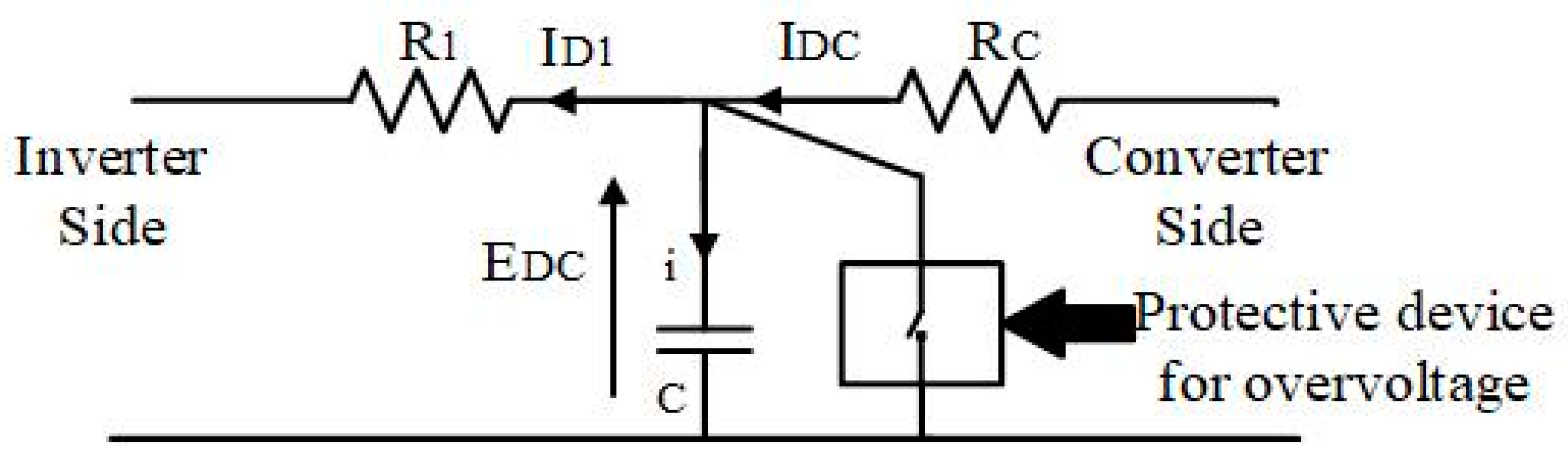
2.2.2. Overvoltage Protection
2.2.3. Grid-Side Inverter
3. Used Optimization Algorithms
3.1. Marine Predator Algorithm
3.1.1. MPA Interpretation
3.1.2. MPA Optimization Scenarios
3.1.3. FAD’s Effect and Eddy Formation
3.1.4. Marine Memory
3.2. Grey Wolf Optimization Algorithm
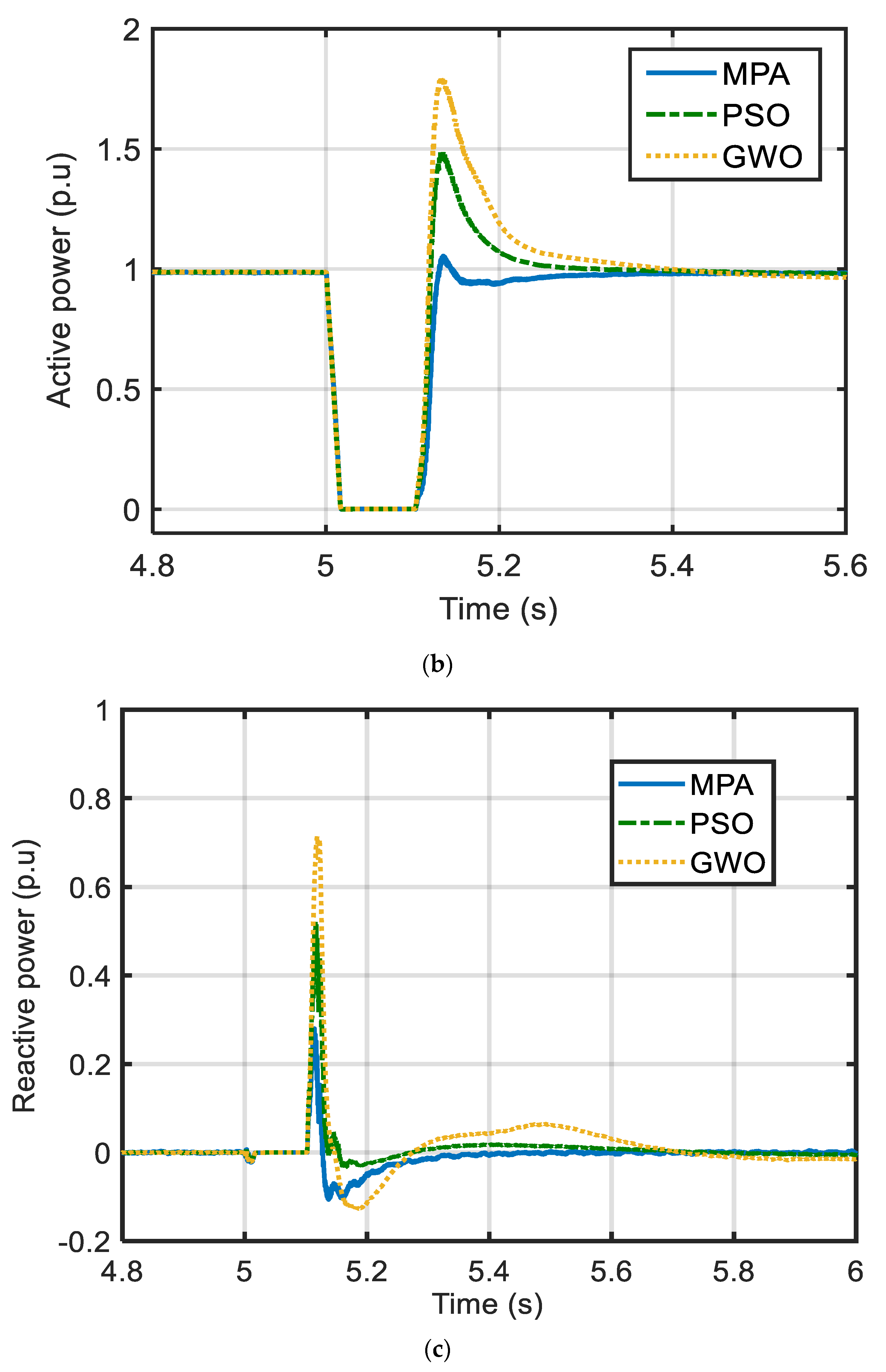
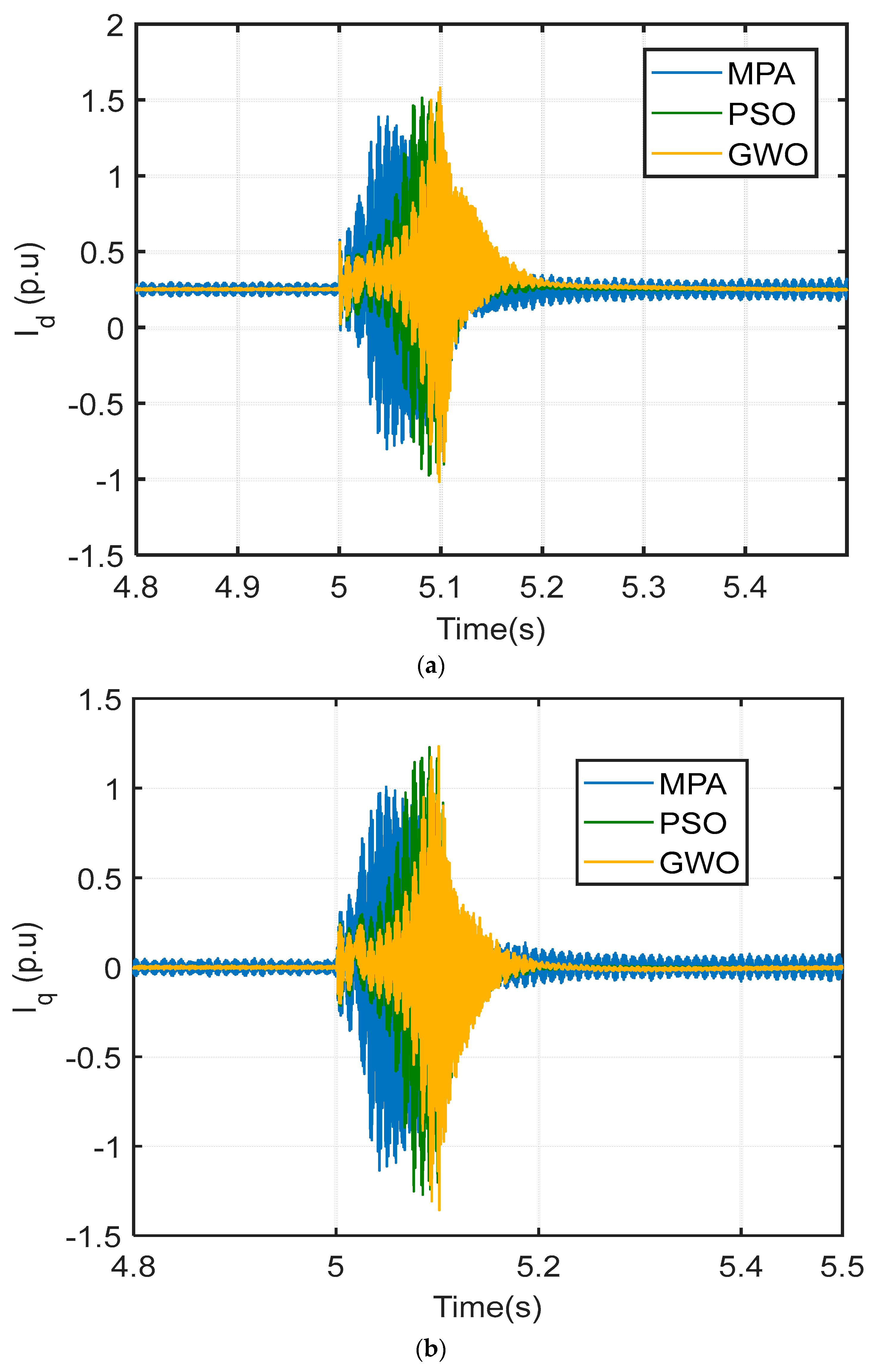
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| a | Ideality factor of diode |
| Im | Maximum output current of PV Array (A) |
| Io | Reverse saturation current of diode (A) |
| Iph | Photo-generated current (A) |
| Isc | Short circuit current of PV module (A) |
| k | Boltzmann constant (1.38065e-23 J/K) |
| Ki | Short-circuit current coefficient |
| Ns | Number of the series connected cells in the module |
| Pm | Maximum Output power of PV Module (W) |
| q | Electron charge (1.6022e-19C) |
| Rs | Series resistance (Ω) |
| Rp | Shunt resistance (Ω) |
| T | Cell Temperature (K) |
| Vm | Maximum output voltage of PV Array (V) |
| Voc | Open circuit voltage of PV module (V) |
| Vth | Thermal voltage |
| Kref | Reference Duty Cycle |
| KM | Proportionality constant |
| VOC-Pilot | Pilot Module Open circuit voltage |
| VO-conv | DC Converter Output Voltage |
| Id-ref | Reference current of direct axis |
| Iq-ref | Reference current of quadrature axis |
| Id | Actual current of direct axis |
| Iq | Quadrature current of direct axis |
| VPCC | Voltage of point of common coupling |
| Kp1 | Proportional Gain of controller 1 |
| Ki1 | Integral Gain of controller 1 |
| Kp2 | Proportional Gain of controller 2 |
| Ki2 | Integral Gain of controller 2 |
| Kp3 | Proportional Gain of controller 3 |
| Ki3 | Integral Gain of controller 3 |
| VDC | DC-link Voltage |
| PPCC | Real Power Output at point of common coupling |
| QPCC | Reactive power injected at point of common coupling |
Appendix A
- Used Code
References
- Gielen, D.; Boshell, F.; Saygin, D.; Bazilian, M.D.; Wagner, N.; Gorini, R. The role of renewable energy in the global energy transformation. Energy Strategy Rev. 2019, 24, 38–50. [Google Scholar] [CrossRef]
- Ufa, R.A.; Malkova, Y.Y.; Rudnik, V.E.; Andreev, M.V.; Borisov, V.A. A review on distributed generation impacts on electric power system. Int. J. Hydrogen Energy 2022, 47, 20347–20361. [Google Scholar] [CrossRef]
- Chen, X.; Mcelroy, M.B.; Wu, Q.; Shu, Y.; Xue, Y. Transition towards higher penetration of renewables: An overview of interlinked technical, environmental and socio-economic challenges. J. Mod. Power Syst. Clean Energy 2018, 7, 1–8. [Google Scholar] [CrossRef]
- Tang, J.; Ni, H.; Peng, R.-L.; Wang, N.; Zuo, L. A review on energy conversion using Hybrid Photovoltaic and Thermoelectric Systems. J. Power Sources 2023, 562, 232785. [Google Scholar] [CrossRef]
- Liao, S. The Russia–Ukraine outbreak and the value of renewable energy. Econ. Lett. 2023, 225, 111045. [Google Scholar] [CrossRef]
- REN21. (n.d.). Renewables 2022 Global Status Report. REN21. Available online: https://www.ren21.net/gsr-2022/chapters/chapter_01/chapter_01/ (accessed on 1 January 2021).
- REN21. (n.d.-a). Renewables 2022 Global Status Report. REN21. Available online: https://www.ren21.net/gsr-2022/chapters/chapter_03/chapter_03/#sub_6 (accessed on 1 January 2021).
- Ibrahim, N.F.; Alkuhayli, A.; Beroual, A.; Khaled, U.; Mahmoud, M.M. Enhancing the functionality of a grid-connected photovoltaic system in a distant Egyptian region using an optimized dynamic voltage restorer: Application of artificial rabbits optimization. Sensors 2023, 23, 7146. [Google Scholar] [CrossRef]
- Elfeky, K.E.; Wang, Q. Techno-Environ-Economic Assessment of photovoltaic and CSP with storage systems in China and Egypt under various climatic conditions. Renew. Energy 2023, 215, 118930. [Google Scholar] [CrossRef]
- D’Adamo, I.; Dell’Aguzzo, A.; Pruckner, M. Residential Photovoltaic and Energy Storage Systems for Sustainable Development: An economic analysis applied to Incentive Mechanisms. Sustain. Dev. 2023. [Google Scholar] [CrossRef]
- Tse, C.K.; Huang, M.; Zhang, X.; Liu, D.; Li, X.L. Circuits and systems issues in power electronics penetrated power grid. IEEE Open J. Circuits Syst. 2020, 1, 140–156. [Google Scholar] [CrossRef]
- Alrumayh, O.; Sayed, K.; Almutairi, A. LVRT and reactive power/voltage support of utility-scale PV power plants during disturbance conditions. Energies 2023, 16, 3245. [Google Scholar] [CrossRef]
- García-Sánchez, T.; Gómez-Lázaro, E.; Molina-García, A. A review and discussion of the grid-code requirements for renewable energy sources in Spain. Renew. Energy Power Qual. J. 2014, 1, 565–570. [Google Scholar] [CrossRef]
- Teodorescu, R.; Liserre, M.; Rodríguez, P. Grid Converters for Photovoltaic and Wind Power Systems; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar] [CrossRef]
- Landera, Y.G.; Zevallos, O.C.; Neto, R.C.; Castro, J.F.d.C.; Neves, F.A.S. A review of grid connection requirements for photovoltaic power plants. Energies 2023, 16, 2093. [Google Scholar] [CrossRef]
- Brooks, D.L.; Patel, M. Panel: Standards & interconnection requirements for wind and solar generation NERC integrating Variable Generation Task Force. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Orlando, FL, USA, 7–10 May 2012. [Google Scholar] [CrossRef]
- Al-Shetwi, A.Q.; Sujod, M.Z.; Blaabjerg, F.; Yang, Y. Fault ride-through control of grid-connected photovoltaic power plants: A Review. Sol. Energy 2019, 180, 340–350. [Google Scholar] [CrossRef]
- Daravath, R.; Sandepudi, S.R. Low voltage ride through control strategy for grid-tied solar photovoltaic inverter. Int. J. Emerg. Electr. Power Syst. 2023. [Google Scholar] [CrossRef]
- Yadav, M.; Pal, N.; Saini, D.K. Low voltage ride through capability for Resilient Electrical Distribution System integrated with Renewable Energy Resources. Energy Rep. 2023, 9, 833–858. [Google Scholar] [CrossRef]
- Talha, M.; Amir, A.; Raihan, S.R.; Abd Rahim, N. Grid-connected photovoltaic inverters with low-voltage ride through for a residential-scale system: A Review. Int. Trans. Electr. Energy Syst. 2020, 31, e12630. [Google Scholar] [CrossRef]
- Abo-Khalil, A.G. Impacts of wind farms on power system stability. In Modeling and Control Aspects of Wind Power Systems; InTechOpen: London, UK, 2013. [Google Scholar] [CrossRef]
- Gatavi, E.; Hellany, A.; Nagrial, M.; Rizk, J. An integrated reactive power control strategy for improving low voltage ride-through capability. Chin. J. Electr. Eng. 2019, 5, 1–14. [Google Scholar] [CrossRef]
- Joshi, P.N.; Dadaso Patil, S. Improving low voltage ride through capabilities of grid connected residential solar PV system using Reactive Power Injection Strategies. In Proceedings of the 2017 International Conference on Technological Advancements in Power and Energy (TAP Energy), Kollam, India, 21–23 December 2017. [Google Scholar] [CrossRef]
- Ntare, R.; Abbasy, N.H.; Youssef, K.H. Low voltage ride through control capability of a large grid connected PV system combining DC Chopper and current limiting techniques. J. Power Energy Eng. 2019, 7, 62–79. [Google Scholar] [CrossRef]
- Çelik, E.; Öztürk, N.; Houssein, E.H. Improved Load frequency control of interconnected power systems using energy storage devices and a new cost function. Neural Comput. Appl. 2022, 35, 681–697. [Google Scholar] [CrossRef]
- Wang, W.; Ge, B.; Bi, D.; Qin, M.; Liu, W. Energy storage based LVRT and stabilizing power control for direct-drive wind power system. In Proceedings of the 2010 International Conference on Power System Technology, Hangzhou, China, 24–28 October 2010. [Google Scholar] [CrossRef]
- Mitali, J.; Dhinakaran, S.; Mohamad, A.A. Energy Storage Systems: A Review. Energy Storage Sav. 2022, 1, 166–216. [Google Scholar] [CrossRef]
- Rincon, D.J.; Mantilla, M.A.; Rey, J.M.; Garnica, M.; Guilbert, D. An overview of flexible current control strategies applied to LVRT capability for grid-connected inverters. Energies 2023, 16, 1052. [Google Scholar] [CrossRef]
- Alhejji, A.; Mosaad, M.I. Performance enhancement of grid-connected PV systems using Adaptive Reference Pi Controller. Ain Shams Eng. J. 2021, 12, 541–554. [Google Scholar] [CrossRef]
- Attou, N.; Zidi, S.-A.; Khatir, M.; Hadjeri, S. Grid-connected photovoltaic system. In ICREEC 2019, Proceedings of the 1st International Conference on Renewable Energy and Energy Conversion; Springer: Berlin/Heidelberg, Germany, 2020; pp. 101–107. [Google Scholar] [CrossRef]
- Elkady, D.A.; Azazy, H.Z.; Mansour, A.S.; Shokrallah, S.S. Adaptive Pi Speed Controller for a universal motor. ERJ. Eng. Res. J. 2015, 38, 101–108. [Google Scholar] [CrossRef]
- Vu, T.N.; Chuong, V.L.; Truong, N.T.; Jung, J.H. Analytical design of fractional-order Pi Controller for Parallel Cascade Control Systems. Appl. Sci. 2022, 12, 2222. [Google Scholar] [CrossRef]
- Celik, E.; Dalcali, A.; Ozturk, N.; Canbaz, R. An adaptive pi controller schema based on Fuzzy Logic Controller for speed control of permanent magnet synchronous motors. In Proceedings of the 4th International Conference on Power Engineering, Energy and Electrical Drives, Istanbul, Turkey, 13–17 May 2013. [Google Scholar] [CrossRef]
- Hasanien, H.M. An adaptive control strategy for low voltage ride through capability enhancement of grid-connected photovoltaic power plants. IEEE Trans. Power Syst. 2016, 31, 3230–3237. [Google Scholar] [CrossRef]
- Çelik, E.; Öztürk, N.; Houssein, E.H. Influence of energy storage device on load frequency control of an interconnected dual-area thermal and Solar Photovoltaic Power System. Neural Comput. Appl. 2022, 34, 20083–20099. [Google Scholar] [CrossRef]
- Deželak, K.; Bracinik, P.; Sredenšek, K.; Seme, S. Proportional-integral controllers performance of a grid-connected solar PV system with particle swarm optimization and Ziegler–Nichols tuning method. Energies 2021, 14, 2516. [Google Scholar] [CrossRef]
- El Moursi, M.S.; Xiao, W.; Kirtley, J.L. Fault ride through capability for grid interfacing large scale PV power plants. IET Gener. Transm. Distrib. 2013, 7, 1027–1036. [Google Scholar] [CrossRef]
- Hossain, K.; Ali, M.H. Low voltage ride through capability enhancement of Grid Connected PV system by SDBR. In Proceedings of the 2014 IEEE PES T&D Conference and Exposition, Chicago, IL, USA, 14–17 April 2014. [Google Scholar] [CrossRef]
- Roslan, M.F.; Al-Shetwi, A.Q.; Hannan, M.A.; Ker, P.J.; Zuhdi, A.W. Particle swarm optimization algorithm-based PI inverter controller for a grid-connected PV system. PLoS ONE 2020, 15, e0243581. [Google Scholar] [CrossRef]
- Prioste, F.B. Optimal Power Flow Using Genetic Algorithm. Anais Do 15. Congresso Brasileiro de Inteligência Computacional. 2021. Available online: https://sbic.org.br/wp-content/uploads/2021/09/pdf/CBIC_2021_paper_144.pdf (accessed on 13 January 2024). [CrossRef]
- AlRashidi, M.R.; AlHajri, M.F.; Al-Othman, A.K.; El-Naggar, K.M. Particle swarm optimization and its applications in Power Systems. In Computational Intelligence in Power Engineering; Springer: Berlin/Heidelberg, Germany, 2010; pp. 295–324. [Google Scholar] [CrossRef]
- Moraes, C.H.; Vilas Boas, J.L.; Lambert-Torres, G.; Andrade, G.C.; Costa, C.I. Intelligent Power Distribution Restoration based on a multi-objective bacterial foraging optimization algorithm. Energies 2022, 15, 1445. [Google Scholar] [CrossRef]
- Ullah, K.; Jiang, Q.; Geng, G.; Rahim, S.; Khan, R.A. Optimal power sharing in microgrids using the artificial bee colony algorithm. Energies 2022, 15, 1067. [Google Scholar] [CrossRef]
- El-Dabah, M.; Ebrahim, M.A.; El-Sehiemy, R.A.; Alaas, Z.; Ramadan, M.M. A modified whale optimizer for single- and multi-objective opf frameworks. Energies 2022, 15, 2378. [Google Scholar] [CrossRef]
- Maaroof, B.B.; Rashid, T.A.; Abdulla, J.M.; Hassan, B.A.; Alsadoon, A.; Mohammadi, M.; Khishe, M.; Mirjalili, S. Current studies and applications of shuffled Frog Leaping Algorithm: A Review. Arch. Comput. Methods Eng. 2022, 29, 3459–3474. [Google Scholar] [CrossRef]
- Mahapatra, S.; Panda, S.; Swain, S.C. A hybrid firefly algorithm and pattern search technique for SSSC based power oscillation damping controller design. Ain Shams Eng. J. 2014, 5, 1177–1188. [Google Scholar] [CrossRef]
- Baghaee, H.R.; Mirsalim, M.; Gharehpetian, G.B. Application of harmony search algorithm in power engineering. In Search Algorithms for Engineering Optimization; InTechOpen: London, UK, 2013. [Google Scholar] [CrossRef]
- Salkuti, S.R. Artificial fish swarm optimization algorithm for Power System State Estimation. Indones. J. Electr. Eng. Comput. Sci. 2020, 18, 1130. [Google Scholar] [CrossRef]
- Rigo-Mariani, R.; Sareni, B.; Roboam, X. Fast power flow scheduling and sensitivity analysis for sizing a microgrid with storage. Math. Comput. Simul. 2017, 131, 114–127. [Google Scholar] [CrossRef]
- Nguyen, K.P.; Fujita, G.; Dieu, V.N. Cuckoo search algorithm for optimal placement and sizing of static var compensator in large-scale power systems. J. Artif. Intell. Soft Comput. Res. 2016, 6, 59–68. [Google Scholar] [CrossRef]
- Houssein, E.; Oliva, D.; Samee, N.; Mahmoud, N.; Emam, M. Liver cancer algorithm: A novel bio-inspired optimizer. Comput. Biol. Med. 2023, 165, 107389. [Google Scholar] [CrossRef]
- Gharehchopogh, F.S.; Ucan, A.; Ibrikci, T.; Arasteh, B.; Isik, G. Slime mould algorithm: A comprehensive survey of its variants and applications. Arch. Comput. Methods Eng. 2023, 30, 2683–2723. [Google Scholar] [CrossRef]
- Wang, G.-G. Moth search algorithm: A bio-inspired metaheuristic algorithm for Global Optimization Problems. Memetic Comput. 2016, 10, 151–164. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, H.; Heidari, A.A.; Gandomi, A.H. Hunger games search: Visions, Conception, implementation, deep analysis, perspectives, and towards performance shifts. Expert Syst. Appl. 2021, 177, 114864. [Google Scholar] [CrossRef]
- Katok, A.; Hasselblatt, B. (Eds.) Handbook of Dynamical Systems; Elsevier: Amsterdam, The Netherlands, 2002. [Google Scholar]
- Tu, J.; Chen, H.; Wang, M.; Gandomi, A.H. The colony predation algorithm. J. Bionic Eng. 2021, 18, 674–710. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Heidari, A.A.; Noshadian, S.; Chen, H.; Gandomi, A.H. Info: An efficient optimization algorithm based on weighted mean of vectors. Expert Syst. Appl. 2022, 195, 116516. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris Hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Lin, F.-J.; Lu, K.-C.; Ke, T.-H. Probabilistic wavelet fuzzy neural network based reactive power control for grid-connected three-phase PV system during grid faults. Renew. Energy 2016, 92, 437–449. [Google Scholar] [CrossRef]
- Lin, F.-J.; Lu, K.-C.; Ke, T.-H.; Yang, B.-H.; Chang, Y.-R. Reactive power control of three-phase grid-connected PV system during grid faults using Takagi-Sugeno Kang probabilistic fuzzy neural network control. IEEE Trans. Ind. Electron. 2015, 62, 5516–5528. [Google Scholar] [CrossRef]
- Li, Z.; Wong, S.-C.; Liu, X.; Huang, Y. Discrete fourier series-based dual-sequence decomposition control of doubly-fed induction generator wind turbine under unbalanced grid conditions. J. Renew. Sustain. Energy 2015, 7, 023130. [Google Scholar] [CrossRef]
- Jaalam, N.; Haidar, A.; Ramli, N.; Ismail, N.; Sulaiman, A. A neuro-fuzzy approach for stator resistance estimation of induction motor. In Proceedings of the International Conference on Electrical, Control and Computer Engineering 2011 (InECCE), Kuantan, Malaysia, 21–22 June 2011; pp. 394–398. [Google Scholar]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Marine Predators Algorithm: A nature-inspired metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar] [CrossRef]
- Sobhy, M.A.; Abdelaziz, A.Y.; Hasanien, H.M.; Ezzat, M. Marine predators algorithm for load frequency control of modern interconnected power systems including renewable energy sources and Energy Storage Units. Ain Shams Eng. J. 2021, 12, 3843–3857. [Google Scholar] [CrossRef]
- Awad, N.H.; Ali, M.Z.; Liang, J.J.; Qu, B.Y.; Suganthan, P.N. Problem definitions and evaluation criteria for the CEC 2017 special session and competition on single objective bound constrained real-parameter numerical optimization. In Technical Report; Nanyang Technological University: Singapore, 2016; pp. 1–34. [Google Scholar]
- Villalva, M.G.; Gazoli, J.R.; Filho, E.R. Modeling and circuit-based simulation of photovoltaic arrays. In Proceedings of the 2009 Brazilian Power Electronics Conference, Bonito-Mato Grosso do Sul, Brazil, 27 September–1 October 2009. [Google Scholar] [CrossRef]
- Ismaeel, A.A.; Houssein, E.H.; Oliva, D.; Said, M. Gradient-based optimizer for parameter extraction in photovoltaic models. IEEE Access 2021, 9, 13403–13416. [Google Scholar] [CrossRef]
- Elazab, O.S.; Hasanien, H.M.; Elgendy, M.A.; Abdeen, A.M. Parameters estimation of single- and multiple-diode photovoltaic model using whale optimisation algorithm. IET Renew. Power Gener. 2018, 12, 1755–1761. [Google Scholar] [CrossRef]
- Hara, S. Parameter extraction of single-diode model from module datasheet information using temperature coefficients. IEEE J. Photovolt. 2021, 11, 213–218. [Google Scholar] [CrossRef]
- Ellithy, H.H.; Taha, A.M.; Hasanien, H.M.; Attia, M.A.; El-Shahat, A.; Aleem, S.H. Estimation of parameters of triple diode photovoltaic models using hybrid particle swarm and grey wolf optimization. Sustainability 2022, 14, 9046. [Google Scholar] [CrossRef]
- Anowar, M.H.; Roy, P. A modified incremental conductance based photovoltaic MPPT Charge Controller. In Proceedings of the 2019 International Conference on Electrical, Computer and Communication Engineering (ECCE), Cox’sBazar, Bangladesh, 7–9 February 2019. [Google Scholar] [CrossRef]
- Islam, G.M.S.; Al-Durra, A.; Muyeen, S.; Tamura, J. Low voltage ride through capability enhancement of grid connected large scale photovoltaic system. In Proceedings of the IECON 2011—37th Annual Conference of the IEEE Industrial Electronics Society, Melbourne, Australia, 7–10 November 2011. [Google Scholar] [CrossRef]
- Takahashi, R.; Tamura, J.; Futami, M.; Kimura, M.; Ide, K. A new control method for wind energy conversion system using a doubly-fed synchronous generator. IEEE Trans. Power Energy 2006, 126, 225–235. [Google Scholar] [CrossRef]
- Elazab, O.S.; Debouza, M.; Hasanien, H.M.; Muyeen, S.M.; Al-Durra, A. Salp Swarm algorithm-based optimal control scheme for LVRT capability improvement of grid-connected photovoltaic power plants: Design and experimental validation. IET Renew. Power Gener. 2020, 14, 591–599. [Google Scholar] [CrossRef]
- Alepuz, S.; Busquets-Monge, S.; Bordonau, J.; Gago, J.; Gonzalez, D.; Balcells, J. Interfacing renewable energy sources to the utility grid using a three-level inverter. IEEE Trans. Ind. Electron. 2006, 53, 1504–1511. [Google Scholar] [CrossRef]
- Filmalter, J.D.; Dagorn, L.; Cowley, P.D.; Taquet, M. First descriptions of the behavior of silky sharks, carcharhinus falciformis, around drifting fish aggregating devices in the Indian Ocean. Bull. Mar. Sci. 2011, 87, 325–337. [Google Scholar] [CrossRef]
- Parouha, R.P.; Das, K.N. A memory based differential evolution algorithm for unconstrained optimization. Appl. Soft Comput. 2016, 38, 501–517. [Google Scholar] [CrossRef]
- Al-Tashi, Q.; Rais, H.; Jadid, S. Feature Selection Method Based on Grey Wolf Optimization for Coronary Artery Disease Classification. In Proceedings of the 2023 Third International Conference on Advances in Electrical, Computing, Communication and Sustainable Technologies (ICAECT), Bhilai, India, 5–6 January 2023; pp. 257–266. [Google Scholar]
- Hasanien, H.M. Performance Improvement of Photovoltaic Power Systems Using an Optimal Control Strategy Based on Whale Optimization Algorithm. Electr. Power Syst. Res. 2018, 157, 168–176. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995. [Google Scholar]
- E.ON Netz. GmbH, Bayreuth, Grid Code-High and Extra-High Voltage, April 2006. Available online: https://docplayer.net/17055474-Grid-code-high-and-extra-high-voltage-tennet-tso-gmbh-bernecker-strasse-70-95448-bayreuth.html (accessed on 13 January 2024).
- Jaalam, N.; Ahmad, A.Z.; Khalid, A.M.; Abdullah, R.; Saad, N.M.; Ghani, S.A.; Muhammad, L.N. Low voltage ride through enhancement using Grey Wolf Optimizer to reduce overshoot current in the grid-connected PV system. Math. Probl. Eng. 2022, 2022, 3917775. [Google Scholar] [CrossRef]
- Han, P.; Fan, G.; Sun, W.; Shi, B.; Zhang, X. Research on identification of LVRT characteristics of photovoltaic inverters based on Data Testing and PSO algorithm. Processes 2019, 7, 250. [Google Scholar] [CrossRef]




| Manufacturer | Kyocera |
|---|---|
| Model | KC200GT |
| Cell Type | Multicrystal |
| Pm (W) | 200 |
| Vm (V) | 26.3 |
| Im (A) | 7.61 |
| VOC (V) | 32.9 |
| ISC (A) | 8.21 |
| Number of series cells | 54 |
| Ki | 0.00318 A/°C |
| Kv | −0.123 V/°C |
| Pm (kW) | 100 |
| Vm (V) | 263 |
| Im (A) | 380.5 |
| Number of series-connected modules | 10 |
| Number of parallel strings | 50 |
| DC-link voltage | 500 V |
| DC-link capacitor | 50,000 µF |
| Limiting reactor (machine base) | 0.2 + j1.0 pu |
| Power converter’s device | IGBT |
| Carrier frequency of PWM | 1 kHz |
| Higher DC voltage limit | 0.75 kV (150% of rating) |
| Lower DC voltage limit | 0.25 kV (50% of rating) |
| Protective device short-circuit parameter for overvoltage | Rsh = 0.2 ohm |
| System Boundaries | Higher Boundaries | Lower Boundaries |
|---|---|---|
| kp1 | 9 | 0.1 |
| ki1 | 9 | 0.1 |
| kp2 | 9 | 0.1 |
| ki2 | 9 | 0.1 |
| kp3 | 9 | 0.1 |
| ki3 | 9 | 0.1 |
| Factor | Integral Square Error |
|---|---|
| Minimum | 2.201 × 10−7 |
| Maximum | 2.35738 × 10−7 |
| Median | 2.24159 × 10−7 |
| Average | 2.24759 × 10−7 |
| Standard Deviation | 3.93938 × 10−10 |
| Variance | 1.55187 × 10−19 |
| Design Variables | MPA | PSO | GWO |
|---|---|---|---|
| kp1 | 0.3042 | 0.2641 | 0.2494 |
| ki1 | 7.4268 | 3.4492 | 6.7142 |
| kp2 | 6.0533 | 1.4964 | 2.4104 |
| ki2 | 6.8165 | 5.9161 | 8.1074 |
| kp3 | 1.75 | 1.5 | 1.4 |
| ki3 | 0.82 | 0.7 | 0.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ellithy, H.H.; Hasanien, H.M.; Alharbi, M.; Sobhy, M.A.; Taha, A.M.; Attia, M.A. Marine Predator Algorithm-Based Optimal PI Controllers for LVRT Capability Enhancement of Grid-Connected PV Systems. Biomimetics 2024, 9, 66. https://doi.org/10.3390/biomimetics9020066
Ellithy HH, Hasanien HM, Alharbi M, Sobhy MA, Taha AM, Attia MA. Marine Predator Algorithm-Based Optimal PI Controllers for LVRT Capability Enhancement of Grid-Connected PV Systems. Biomimetics. 2024; 9(2):66. https://doi.org/10.3390/biomimetics9020066
Chicago/Turabian StyleEllithy, Hazem Hassan, Hany M. Hasanien, Mohammed Alharbi, Mohamed A. Sobhy, Adel M. Taha, and Mahmoud A. Attia. 2024. "Marine Predator Algorithm-Based Optimal PI Controllers for LVRT Capability Enhancement of Grid-Connected PV Systems" Biomimetics 9, no. 2: 66. https://doi.org/10.3390/biomimetics9020066







