A Study on Site Selection for Regional Air Rescue Centers Based on Multi-Objective Jellyfish Search Algorithm
Abstract
:1. Introduction
2. Air Rescue Site
2.1. Definition of the Air Rescue Site
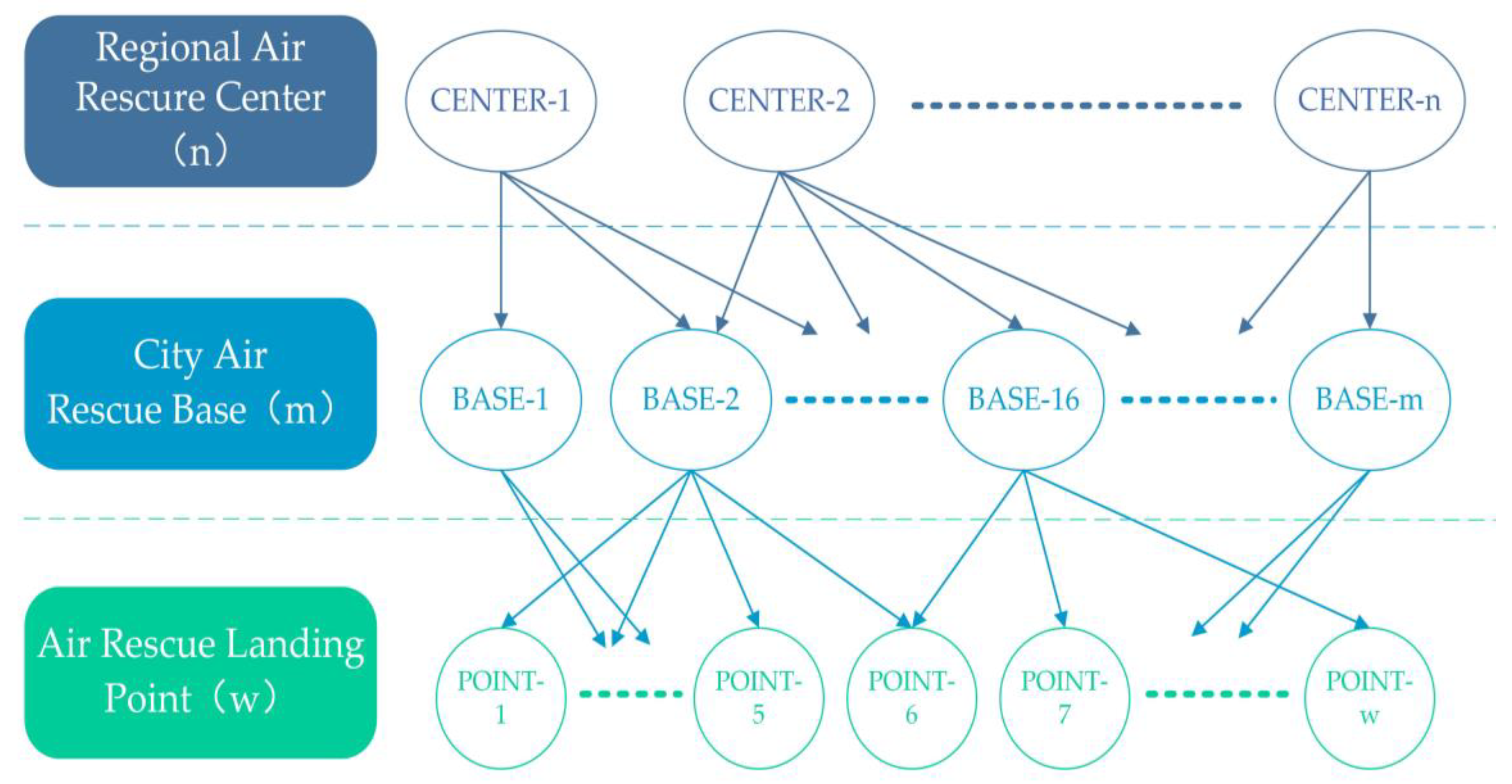
2.2. Classification of the Air Rescue Site
2.2.1. Regional Air Rescue Center
2.2.2. City Air Rescue Base
2.2.3. Air Rescue Landing Point
2.3. Features of Regional Air Rescue Center
- Regional aviation emergency rescue centers must be equipped with runways, aprons, hangars, command centers, office buildings, training centers, material warehouses, maintenance stations, small aviation parts warehouses, medical stations, and fire stations for use in executing aviation emergency rescue tasks. If these facilities already exist within an airport and their operation does not interfere with aviation emergency rescue functions, they may be used; otherwise, additional facilities must be constructed.
- Regional aviation emergency rescue centers require call centers, which may also utilize civil aviation airports adjacent to the rescue site or other relevant municipal call centers in the area.
- The types of aircraft commonly available at regional aviation emergency rescue centers are fixed-wing aircraft and helicopters. The number of rescue helicopters required in different regions will be determined based on demand, with a minimum of three for rescue purposes and two for training purposes, and at least one fixed-wing aircraft.
- The types of materials commonly available at regional aviation emergency rescue centers should meet the needs of implementing aviation emergency rescue tasks for public health emergencies, traffic emergencies, fire emergencies, earthquake emergencies, industrial emergencies, medical assistance, etc. The number of materials available at regional aviation emergency rescue centers will be determined based on the population of the region, with a minimum requirement of 0.0001% of the total population, multiplied by the corresponding multiple based on the type and frequency of use of the materials.
- Personnel will be allocated based on their job positions and the number of aircraft, divided into ground personnel and onboard personnel. Ground personnel will be allocated according to their job positions to meet minimum requirements, while on-board personnel will be allocated based on the operating requirements of the rescue aircraft and the number of aircraft used.
3. Regional Air Rescue Center Site Selection Issues
3.1. Problem Description
3.2. Analysis of Influencing Factors
3.2.1. Construction Cost Factor
3.2.2. Radiation Factor
3.2.3. Response Time Factor
4. Establishment of Site Selection Model for Regional Air Rescue Center
4.1. Mathematical Description of Site Selection Problem
- It can make full use of the implementation equipment and various resources of existing civil transport airports, thus saving costs.
- China has a large number of civil transport airports, providing sufficient alternative options for the site selection of emergency rescue centers.
- China’s civil transport airports are located in densely populated, economically developed, or strategically important areas where there is a greater demand for emergency rescue, making it logical to establish emergency rescue centers in these areas.
4.2. Model Assumptions
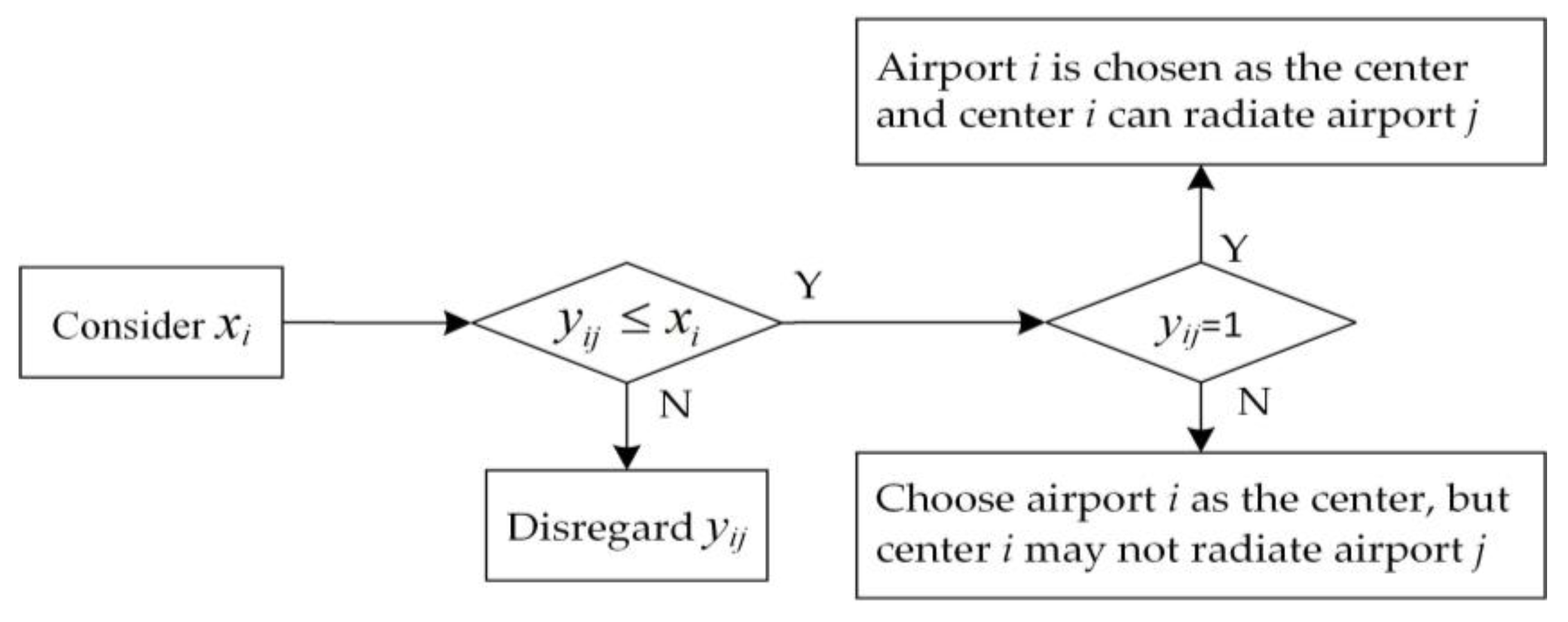
4.3. Definition of Decision Variables
4.4. Establishment of Objective Function
4.4.1. Construction Cost Objective
4.4.2. Response Time Objective
4.4.3. Radiation Degree Objective
- Radiation degree coefficient
- 2.
- Vulnerability coefficient
4.5. Constraint Construction

5. Model Solution
5.1. Methods for Solving Multi-Objective Problems
- The model is nonlinear, which can be observed from Equations (7) and (11).
- The decision variables xi and yij are high-dimensional variables.
- The time complexity of an algorithm is a measure of the amount of time required for the algorithm to solve a problem of a given size. In the case of an n-dimensional 0–1 vector, the time complexity of the algorithm is O(2n), which is a characteristic of exponential time complexity. In contrast, polynomial time complexity implies that the running time of the algorithm grows polynomially with the size of the input, making it more efficient than exponential time complexity. Despite the algorithm’s exponential time complexity, it is still possible to verify a feasible solution within polynomial time. Therefore, the problem addressed in this paper is classified as an NP-hard problem. NP-hard problems are a class of problems that are known to be difficult to solve and are thought to require exponential time complexity.
- It has only two internal parameters;
- It is easy to encode;
- JS can search for the optimal position better than other algorithms;
- It requires less time and has a faster convergence rate than other algorithms [32];
- JS is significantly better than the firefly Algorithm (FA), gravitational search algorithm (GSA), artificial bee colony algorithm (ABC), differential evolution (DE), particle swarm optimization (PSO), and genetic algorithm (GA) in mathematical benchmark tests [30].
- Initialization of population generation;
- Determination of the initial optimal position;
- Updating time control parameter C(t);
- Updating jellyfish positions based on the direction of ocean currents;
- Updating the movement types of individuals based on their movement type;
- Evaluating new fitness and updating the optimal position;
- Evaluating the fitness of the latest jellyfish position;
- Determining whether the maximum number of iterations has been reached.

5.2. Algorithm Design
5.2.1. Population Initialization
5.2.2. Time Control Mechanism
5.2.3. Boundary Constraint Mechanism
5.2.4. Optimization Search Stage
- Flow-following search
- 2.
- Population movement
5.2.5. Update Location Stage
6. Case Study
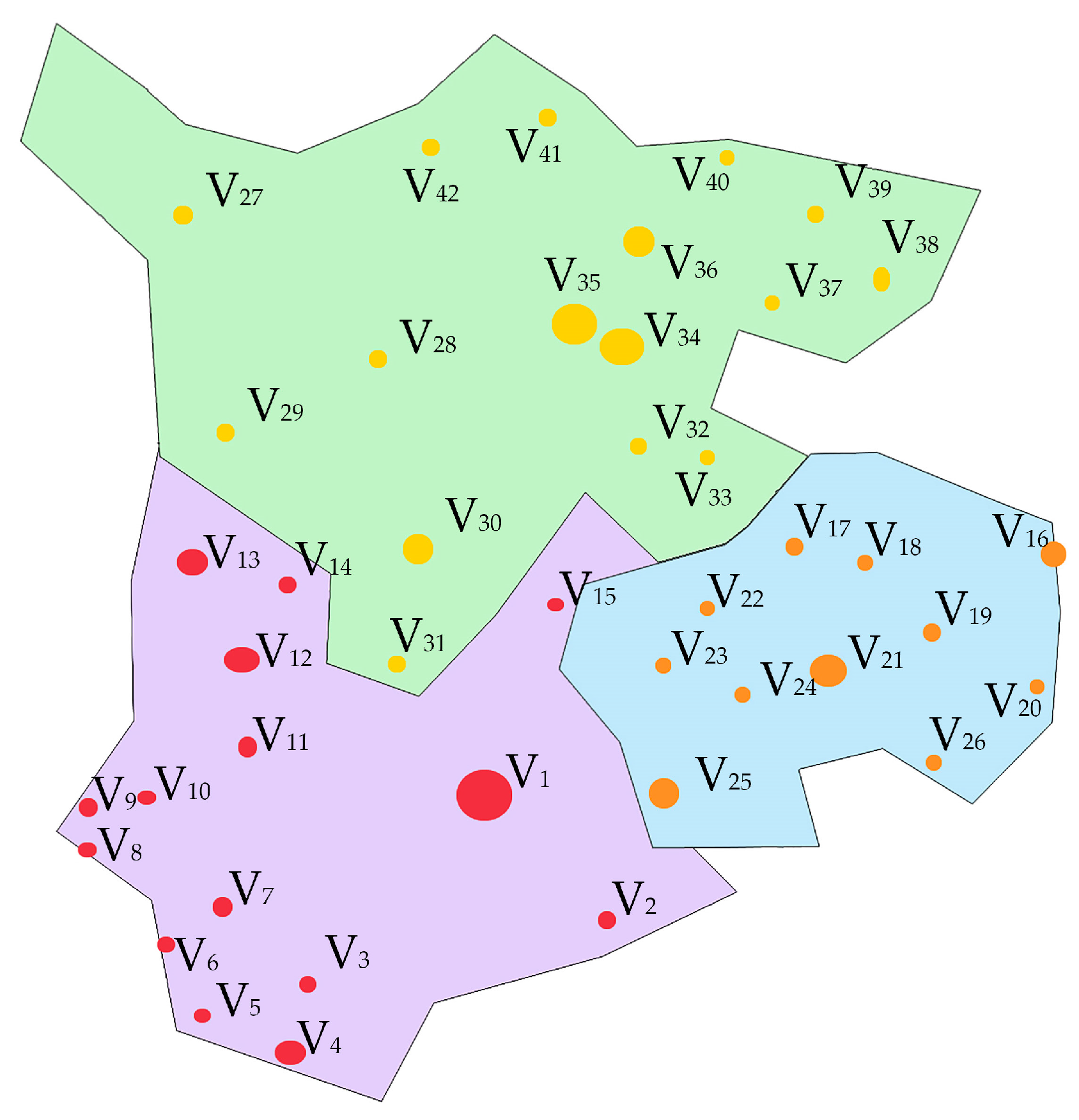
6.1. Case Background
6.2. Model Parameter Determination
6.2.1. Construction Cost Coefficient
6.2.2. Fragility Coefficient
6.2.3. Radiation Degree
6.3. Multi-Objective Jellyfish Search Algorithm for Site Selection
6.3.1. Algorithm Parameter Setting
6.3.2. Algorithmic Solution Search and Update
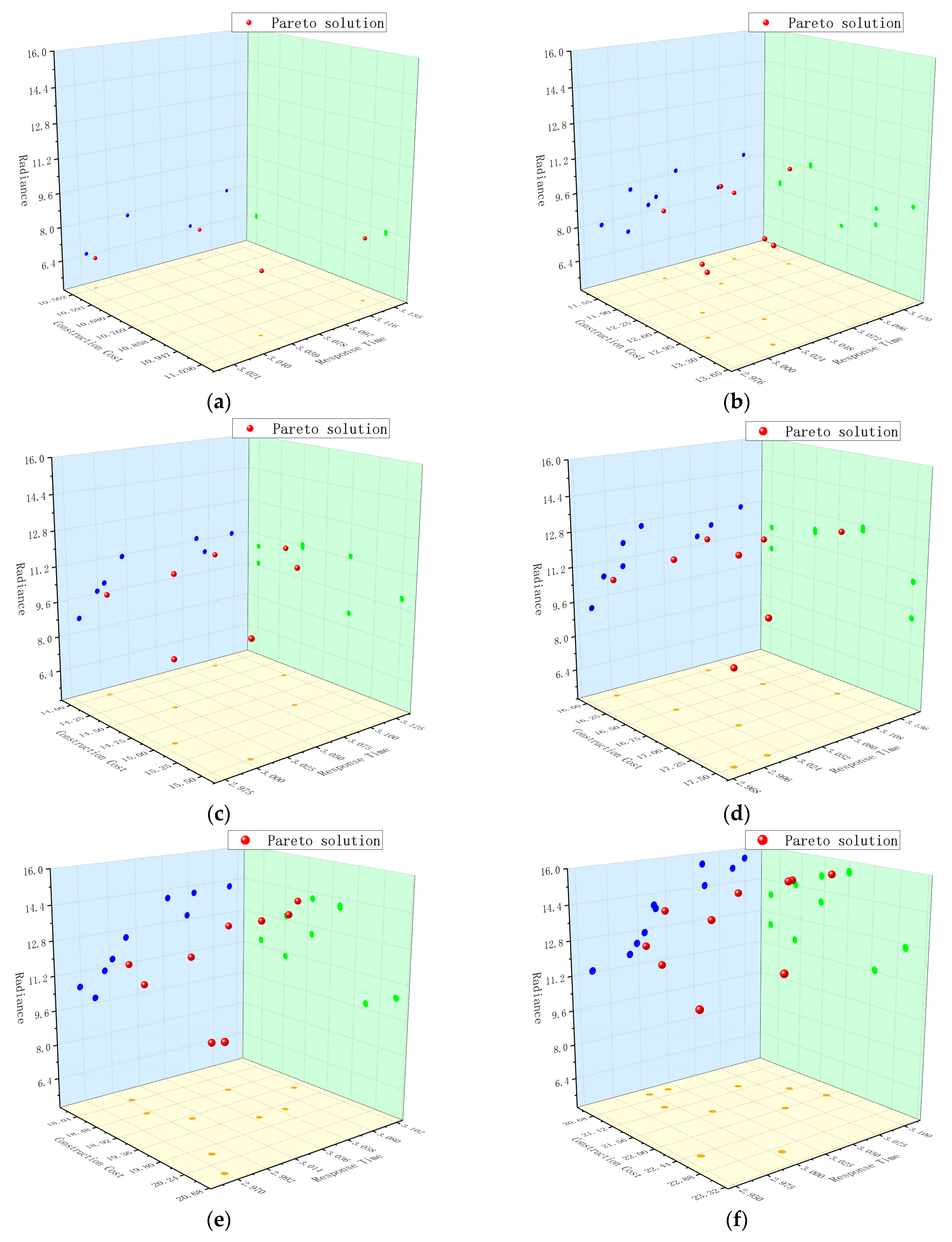
6.3.3. Example Analysis of Site Selection Results
7. Conclusions
- The paper proposes a solution approach that considers the construction cost, response time, and radiance objectives among the programs that meet the constraints of full coverage and siting points.
- The paper establishes a mathematical siting model using a multi-objective 0–1 optimization model, vulnerability coefficient, construction cost coefficient, and radiance coefficient. The model aims to minimize the construction cost and response time, maximize regional radiance as objective functions, and take different siting options as decision variables, and full coverage, central point effectiveness, and the number of siting points as constraints.
- The paper designs a multi-objective jellyfish search algorithm to solve the developed model, which is a multi-objective nonlinear optimization model and an NP-hard problem. The algorithm is designed to solve the model by initializing the population, time control mechanism, boundary restriction mechanism, merit-seeking search, and update position.
- The paper selects a region for the case study of the siting model. Through the multi-objective jellyfish search algorithm, the corresponding Pareto solution sets for different site selection points are solved, and the results demonstrate that the proposed method is well-applied to the regional aviation emergency rescue center siting problem.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Acronyms & Symbols | Implication |
| ABC | Artificial bee colony algorithm |
| AHP | Analytic hierarchy process |
| DE | Differential evolution |
| FA | Firefly algorithm |
| GA | Genetic algorithm |
| GIS | Geographic information system |
| GSA | Gravitational search algorithm |
| JS | Artificial jellyfish search algorithm |
| MOJS | Multi-objective jellyfish search algorithm |
| NSGA-II | Non-dominated sorting genetic algorithm II |
| PSO | Particle swarm optimization |
| Ai | The construction cost coefficient of node i |
| Bi | The response time coefficient |
| M | The maximum number of regional air rescue centers that can be selected |
| Npop | Population size |
| Ti | The maximum response time that can be radiated within the radiation range of node i |
| tij | The rescue response time from node i to node j |
| TR | The flexible time for emergency rescue maneuvers |
| V | The set of nodes to be selected |
| τij | The radiation degree coefficient from the central node i to the radiation node j |
References
- Zhong, Z.; Zhang, M. Prospect of “14th Five-Year Plan” Aviation Emergency Rescue. Civ. Aviat. Today 2022, 1, 68–73. [Google Scholar]
- Available online: http://www.aopa.org.cn/usr/1/upload/file/20200617/15923799789831740.pdf (accessed on 3 October 2022).
- Cao, Q.; Chen, W.X. A review of research on siting of emergency facilities. Comput. Eng. 2019, 45, 26–37. [Google Scholar]
- Maleki, M.; Majlesinasab, N.; Sepehri, M.M. Two new models for the redeployment of ambulances. Comput. Ind. Eng. 2014, 78, 271–284. [Google Scholar] [CrossRef]
- Su, Q.; Luo, Q.; Huang, S.H. Cost-effective analyses for emergency medical services deployment: A case study in Shanghai. Int. J. Prod. Econ. 2015, 163, 112–123. [Google Scholar] [CrossRef]
- Sudtachat, K.; Mayorga, M.E.; Mclay, L.A. A nested-compliance table policy for emergency medical service systems under relocation. Omega 2016, 58, 154–168. [Google Scholar] [CrossRef]
- Chanta, S.; Mayorga, M.E.; Mclay, L.A. The minimum p-envy location problem with a requirement on minimum survival rate. Comput. Ind. Eng. 2014, 74, 228–239. [Google Scholar] [CrossRef]
- Zheng, B.; Ma, Z.; Li, S. The site-intermodal problem of emergency logistics system based on two-level planning. Syst. Sci. Math. 2013, 33, 1045–1060. [Google Scholar]
- Zheng, B.; Ma, Z.; Li, S. Optimization of emergency logistics system based on two-layer planning in the early post-earthquake period. J. Syst. Eng. 2014, 29, 113–125. [Google Scholar]
- Chen, P.; Zhang, J.; Sun, Y.; Zhang, L.; Liu, J. Optimal layout of urban fire emergency supplies storage. Fire Sci. Technol. 2015, 34, 110–113. [Google Scholar]
- Song, Y.H.; Su, B.B.; Huo, F.Z.; Ning, J.; Fang, D. Rapid site selection for emergency material distribution center considering dynamic demand. Chin. J. Saf. Sci. 2019, 29, 172–177. [Google Scholar]
- Kilci, F.; Kara, B.Y.; Bozkaya, B. Locating temporary shelter areas after an earthquake: A case for Turkey. Eur. J. Oper. Res. 2015, 243, 323–332. [Google Scholar] [CrossRef]
- Bayram, V.; Tansel, B.; Yaman, H. Compromising system and user interests in shelter location and evacuation planning. Transp. Res. Part B Methodol. 2015, 72, 146–163. [Google Scholar] [CrossRef]
- Pi, J.; Jia, M.; Qi, F. Optimization of mega-city aviation emergency rescue site layout. Saf. Environ. Eng. 2020, 27, 140–146. [Google Scholar]
- Li, Z.; Jiao, Q.Q.; Zhou, Y.F. A multi-objective dynamic localization-allocation model for post-earthquake emergency supplies supply points. Comput. Eng. 2017, 43, 281–288. [Google Scholar]
- Kessler, C. Helicopter emergency medical service motivation for focused research. CEAS Aeronaut. J. 2015, 6, 337–394. [Google Scholar] [CrossRef]
- Li, Y.; Li, R. Research on the construction of aviation emergency rescue standard system in China. Chin. J. Saf. Sci. 2019, 29, 178–184. [Google Scholar]
- Yang, W.J.; Liu, S.J. Research on the layout of general aviation emergency rescue sites. China Civ. Aviat. 2009, 6, 27–29. [Google Scholar]
- Li, H. China’s aviation emergency rescue status and development strategy. Sci. Technol. Innov. Appl. 2019, 6, 135–136. [Google Scholar]
- Zhu, L. Research on the Site Selection of Emergency Rescue Stations for Urban Rail Transportation Based on Complex Network Theory. Master’s Thesis, Southeast University, Nanjing, China, May 2018. [Google Scholar]
- Wang, H.; Shao, T.; Xu Chen, C. Research on the siting of civil aviation emergency rescue regional support center. Henan Sci. 2018, 36, 1119–1125. [Google Scholar]
- Tang, D.H.; Wei, X. E-commerce distribution center site selection based on an economical genetic algorithm. Comput. Simul. 2022, 39, 158–162. [Google Scholar]
- Feng, Y.; Xie, Q. Siting and scheduling of emergency logistics facilities based on genetic algorithm. Technol. Ind. 2021, 21, 102–106. [Google Scholar]
- Chen, Y.; Zhang, H. Two-tier medical facility siting problem and taboo search algorithm. Oper. Res. Manag. 2021, 30, 56–63. [Google Scholar]
- Xu, Y. Optimization Study of Multi-Objective Urban Domestic Waste Reverses Logistics Network. Master’s Thesis, Shanghai University, Shanghai, China, 2021. [Google Scholar]
- Wang, K. Distributed Power Source Siting and Capacity Determination Based on Whale Particle Swarm Hybrid Algorithm. Master’s Thesis, Shenyang Agricultural University, Shenyang, China, 2022. [Google Scholar]
- Yao, J. A multi-objective fire station siting planning model based on particle swarm algorithm. Electron. Technol. Softw. Eng. 2021, 20, 114–116. [Google Scholar]
- Liu, J.; Yang, C. Application of particle swarm Drosophila hybrid improvement algorithm in base station siting optimization problem. Comput. Digit. Eng. 2021, 49, 1341–1345+1356. [Google Scholar]
- Ge, C.; Wang, X.; Guan, X. A multi-covering model and its algorithm for facility location response for large-scale emergencies. Oper. Res. Manag. Sci. 2011, 20, 50–56. [Google Scholar]
- Chou, J.S.; Truong, D.N. Multi-objective optimization inspired by the behavior of jellyfish for solving structural design problems. Chaos Solitons Fractals 2020, 135, 109738. [Google Scholar] [CrossRef]
- Hassan, B.A.; Rashid, T.A. Operational framework for recent advances in backtracking search optimization algorithm: A systematic review and performance evaluation. Appl. Math. Comput. 2020, 370, 124919. [Google Scholar]
- Pramudita, A.; Taniguchi, E.; Qureshi, A.G. Location and routing problems of debris collection operation after disasters with realistic case study. Procedia-Soc. Behav. Sci. 2014, 125, 445–458. [Google Scholar] [CrossRef] [Green Version]
- Chou, J.S.; Truong, D.N. A novel metaheuristic optimizer inspired by the behavior of jellyfish in the ocean. Appl. Math. Comput. 2021, 389, 125535. [Google Scholar] [CrossRef]
- Fu, R.H.; Qin, T.; Zhang, Q.; Xing, J.S. Research on control of electro-hydraulic servo system based on improved artificial jellyfish search algorithm [J/OL]. Mach. Tools Hydraul. 2022, 50, 1–6. [Google Scholar]
- Zhao, X.; Wang, H.; Liu, C.; Li, L.; Bo, S.; Ji, J. An artificial jellyfish search optimization algorithm for human brain function division. Comput. Sci. Explor. 2022, 16, 1829–1841. [Google Scholar]







| Node | Node | ||||||
|---|---|---|---|---|---|---|---|
| 0.836 | V4 | 0.786 | 6.57096 | 0.545 | V7 | 0.343 | 1.86935 |
| 0.836 | V5 | 0.322 | 2.69192 | 0.545 | V8 | 0.712 | 3.8804 |
| 0.836 | V6 | 0.336 | 2.80896 | 0.326 | V12 | 0.283 | 0.92258 |
| 0.836 | V8 | 0.124 | 1.03664 | 0.326 | V11 | 0.452 | 1.47352 |
| 0.836 | V9 | 0.833 | 6.96388 | 0.326 | V13 | 0.251 | 0.81826 |
| 0.836 | V11 | 0.116 | 6.78832 | 0.326 | V14 | 0.097 | 0.31622 |
| 0.836 | V10 | 0.812 | 0.96976 | Total | 37.11 | ||
| Node | Ai | Node | Ai | Node | Ai | Node | Ai | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| V1 | 1 | 0.994 | V12 | 2 | 0.78 | V23 | 2.5 | 0.762 | V34 | 1 | 0.926 |
| V2 | 2.5 | 0.694 | V13 | 2 | 0.702 | V24 | 2 | 0.811 | V35 | 1 | 0.938 |
| V3 | 2.5 | 0.716 | V14 | 2.5 | 0.707 | V25 | 2.5 | 0.691 | V36 | 2 | 0.815 |
| V4 | 2 | 0.762 | V15 | 2.5 | 0.7 | V26 | 2.5 | 0.512 | V37 | 2.5 | 0.689 |
| V5 | 2.5 | 0.693 | V16 | 2 | 0.786 | V27 | 2.5 | 0.603 | V38 | 2.5 | 0.677 |
| V6 | 2.5 | 0.705 | V17 | 2.5 | 0.682 | V28 | 2.5 | 0.536 | V39 | 2.5 | 0.615 |
| V7 | 2.5 | 0.68 | V18 | 2.5 | 0.725 | V29 | 2 | 0.732 | V40 | 2.5 | 0.623 |
| V8 | 2.5 | 0.731 | V19 | 2.5 | 0.703 | V30 | 2.5 | 0.653 | V41 | 2.5 | 0.582 |
| V9 | 2.5 | 0.713 | V20 | 2.5 | 0.701 | V31 | 2.5 | 0.702 | V42 | 2.5 | 0.568 |
| V10 | 2.5 | 0.728 | V21 | 1.5 | 0.895 | V32 | 2.5 | 0.693 | |||
| V11 | 2.5 | 0.714 | V22 | 2.5 | 0.722 | V33 | 1 | 0.926 |
| V1 | V2 | V3 | V4 | V5 | V6 | V7 | V8 | V9 | V10 | V11 | V12 | V13 | V14 | V15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| V1 | 1.000 | 0.715 | 0.394 | 0.000 | 0.000 | 0.000 | 0.309 | 0.000 | 0.000 | 0.000 | 0.535 | 0.360 | 0.000 | 0.279 | 0.630 |
| V2 | 0.715 | 1.000 | 0.123 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| V3 | 0.394 | 0.123 | 1.000 | 1.000 | 0.940 | 0.830 | 0.916 | 0.445 | 0.272 | 0.457 | 0.440 | 0.000 | 0.000 | 0.000 | 0.000 |
| V4 | 0.000 | 0.000 | 1.000 | 1.000 | 0.981 | 0.764 | 0.762 | 0.258 | 0.000 | 0.104 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| V5 | 0.000 | 0.000 | 0.940 | 0.981 | 1.000 | 1.000 | 0.912 | 0.637 | 0.474 | 0.521 | 0.271 | 0.000 | 0.000 | 0.000 | 0.000 |
| V6 | 0.000 | 0.000 | 0.830 | 0.764 | 1.000 | 1.000 | 1.000 | 0.896 | 0.770 | 0.796 | 0.572 | 0.000 | 0.000 | 0.000 | 0.000 |
| V7 | 0.309 | 0.000 | 0.916 | 0.762 | 0.912 | 1.000 | 1.000 | 0.837 | 0.751 | 0.854 | 0.757 | 0.433 | 0.000 | 0.000 | 0.000 |
| V8 | 0.000 | 0.000 | 0.445 | 0.258 | 0.637 | 0.896 | 0.837 | 1.000 | 1.000 | 1.000 | 0.687 | 0.471 | 0.000 | 0.000 | 0.000 |
| V9 | 0.000 | 0.000 | 0.272 | 0.000 | 0.474 | 0.770 | 0.751 | 1.000 | 1.000 | 1.000 | 0.747 | 0.599 | 0.368 | 0.117 | 0.000 |
| V10 | 0.000 | 0.000 | 0.457 | 0.104 | 0.521 | 0.796 | 0.854 | 1.000 | 1.000 | 1.000 | 0.924 | 0.752 | 0.493 | 0.428 | 0.000 |
| V11 | 0.535 | 0.000 | 0.440 | 0.000 | 0.271 | 0.572 | 0.757 | 0.687 | 0.747 | 0.924 | 1.000 | 0.993 | 0.671 | 0.754 | 0.000 |
| V12 | 0.360 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.433 | 0.471 | 0.599 | 0.752 | 0.993 | 1.000 | 0.935 | 0.998 | 0.000 |
| V13 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.368 | 0.493 | 0.671 | 0.935 | 1.000 | 0.972 | 0.000 |
| V14 | 0.279 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.117 | 0.428 | 0.754 | 0.998 | 0.972 | 1.000 | 0.408 |
| V15 | 0.630 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.408 | 1.000 |
| Number of Sites | Z1 | Z2 | Z3 | Site Selection Results | Number of Sites | Z1 | Z2 | Z3 | Site Selection Results |
|---|---|---|---|---|---|---|---|---|---|
| 5 | 8.5 | 3.1096 | 5.73 | 1,10,21,29,34 | 9 | 16 | 3.0871 | 11.589 | 1,6,9,16,21,25,29,34,35 |
| 6 | 11 | 3.1284 | 7.939 | 1,6,9,21,29,34 | 9 | 17.5 | 3.0111 | 10.819 | 1,6,12,16,18,21,29,35,38 |
| 6 | 11 | 3.0537 | 7.846 | 1,3,9,21,29,34 | 9 | 16 | 2.9926 | 10.511 | 1,6,9,16,18,21,29,34,35 |
| 6 | 10.5 | 3.0995 | 6.547 | 1,6,12,21,29,34 | 9 | 17.5 | 2.9802 | 9.159 | 1,6,12,16,18,21,25,29,34,35 |
| 6 | 10.5 | 3.0248 | 6.454 | 1,3,12,21,29,34 | 10 | 19 | 3.0945 | 14.104 | 1,6,9,16,18,21,23,29,34,35 |
| 7 | 12 | 3.1189 | 9.803 | 1,6,9,21,29,34,35 | 10 | 19.5 | 3.0629 | 14.036 | 1,3,6,9,18,21,23,29,34,35 |
| 7 | 12 | 3.0549 | 9.71 | 1,3,9,21,29,34,35 | 10 | 19.5 | 3.0404 | 13.968 | 1,6,12,16,18,21,27,29,35,38 |
| 7 | 13.5 | 3.0152 | 9.253 | 1,6,9,18,21,29,34 | 10 | 18.5 | 3.0568 | 12.996 | 1,6,9,16,18,21,25,29,34,35 |
| 7 | 13 | 3.0371 | 8.632 | 1,6,12,18,21,29,34 | 10 | 19 | 3.0057 | 12.415 | 1,6,8,9,17,18,21,29,34,35 |
| 7 | 11.5 | 3.0942 | 8.411 | 1,6,12,21,29,34,35 | 10 | 18 | 2.9946 | 11.511 | 1,6,12,16,18,21,27,29,34,35 |
| 7 | 11.5 | 3.0302 | 8.318 | 1,3,12,21,29,34,35 | 10 | 18.5 | 2.9884 | 11.023 | 1,6,9,16,18,21,27,29,34,35 |
| 7 | 13 | 2.9905 | 7.861 | 1,6,9,16,21,29,34 | 10 | 20.5 | 2.9691 | 10.488 | 1,6,12,16,18,21,27,29,32,34,35 |
| 7 | 12.5 | 3.0124 | 7.24 | 1,6,12,16,21,29,34 | 10 | 20 | 2.9804 | 9.836 | 1,6,12,18,21,22,27,29,34,38 |
| 8 | 15 | 3.0884 | 11.315 | 1,3,9,18,25,29,34,35 | 11 | 22 | 3.0995 | 15.511 | 1,3,6,8,9,10,18,21,29,34,35 |
| 8 | 14.5 | 3.1227 | 11.247 | 1,6,9,18,21,29,34,35 | 11 | 22 | 3.0586 | 15.477 | 1,6,12,16,18,21,22,27,29,35,38 |
| 8 | 14.5 | 3.0211 | 11.117 | 1,6,12,16,18,21,29,34 | 11 | 21.5 | 3.0877 | 15.089 | 1,3,6,9,16,18,21,23,29,34,35 |
| 8 | 14 | 3.0963 | 10.589 | 1,6,12,18,21,29,34,35 | 11 | 21 | 3.0608 | 14.434 | 1,6,12,16,18,21,23,27,29,34,35 |
| 8 | 15.5 | 3.0055 | 10.039 | 1,6,12,16,18,21,29,34,35 | 11 | 21.5 | 3.0143 | 13.853 | 1,3,6,8,9,18,21,23,29,34,35 |
| 8 | 14 | 2.9994 | 9.725 | 1,3,9,16,21,29,34,35 | 11 | 20.5 | 3.0159 | 13.683 | 1,6,12,16,18,21,25,29,34,35,38 |
| 8 | 15 | 2.9839 | 8.647 | 1,6,9,16,18,21,29,34 | 11 | 23 | 3.0058 | 12.635 | 1,6,9,16,17,18,21,27,29,35,38 |
| 9 | 17 | 3.1350 | 12.688 | 1,3,6,9,18,21,29,34,35 | 11 | 20.5 | 2.9989 | 12.188 | 1,6,9,12,16,18,21,25,29,34,35 |
| 9 | 17 | 3.0299 | 12.555 | 1,6,12,16,18,21,27,29,34 | 11 | 21 | 2.9926 | 11.725 | 1,6,9,16,18,21,23,27,29,34,35 |
| 9 | 16.5 | 3.1021 | 12.033 | 1,6,9,16,21,23,29,34,35 | 11 | 22.5 | 2.9609 | 11.274 | 1,6,9,16,18,21,22,27,29,35,38 |
| 9 | 16.5 | 3.0118 | 11.903 | 1,6,9,18,21,23,29,34,35 |
| Regional Center Point | Construction Cost | Radiation Point | Radiation Intensity | Regional Center Point | Construction Cost | Radiation Point | Radiation Intensity |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 0.71094 | 21 | 1.5 | 19 | 0.835035 |
| 3 | 0.391298 | 20 | 0.567248 | ||||
| 15 | 0.626637 | 22 | 0.777097 | ||||
| 10 | 2.5 | 4 | 0.075634 | 23 | 0.703301 | ||
| 5 | 0.379504 | 24 | 0.895 | ||||
| 6 | 0.579144 | 25 | 0.570339 | ||||
| 7 | 0.621756 | 26 | 0.758657 | ||||
| 8 | 0.728 | 34 | 1 | 28 | 0.481791 | ||
| 9 | 0.728 | 32 | 0.81762 | ||||
| 11 | 0.67252 | 33 | 0.772973 | ||||
| 12 | 0.547789 | 35 | 0.926 | ||||
| 13 | 0.358833 | 36 | 0.888472 | ||||
| 14 | 0.311779 | 37 | 0.736854 | ||||
| 29 | 2.5 | 27 | 0.317826 | 38 | 0.345245 | ||
| 30 | 0.313934 | 39 | 0.509028 | ||||
| 31 | 0.145489 | 40 | 0.567362 | ||||
| 21 | 1.5 | 16 | 0.421572 | 41 | 0.499575 | ||
| 17 | 0.787821 | 42 | 0.358454 | ||||
| 18 | 0.815967 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, Y.; Zhao, Y.; Fang, N.; Huang, J. A Study on Site Selection for Regional Air Rescue Centers Based on Multi-Objective Jellyfish Search Algorithm. Biomimetics 2023, 8, 254. https://doi.org/10.3390/biomimetics8020254
Liao Y, Zhao Y, Fang N, Huang J. A Study on Site Selection for Regional Air Rescue Centers Based on Multi-Objective Jellyfish Search Algorithm. Biomimetics. 2023; 8(2):254. https://doi.org/10.3390/biomimetics8020254
Chicago/Turabian StyleLiao, Yong, Yiyang Zhao, Na Fang, and Jie Huang. 2023. "A Study on Site Selection for Regional Air Rescue Centers Based on Multi-Objective Jellyfish Search Algorithm" Biomimetics 8, no. 2: 254. https://doi.org/10.3390/biomimetics8020254





