3D Zero Poisson’s Ratio Honeycomb Structure for Morphing Wing Applications
Abstract
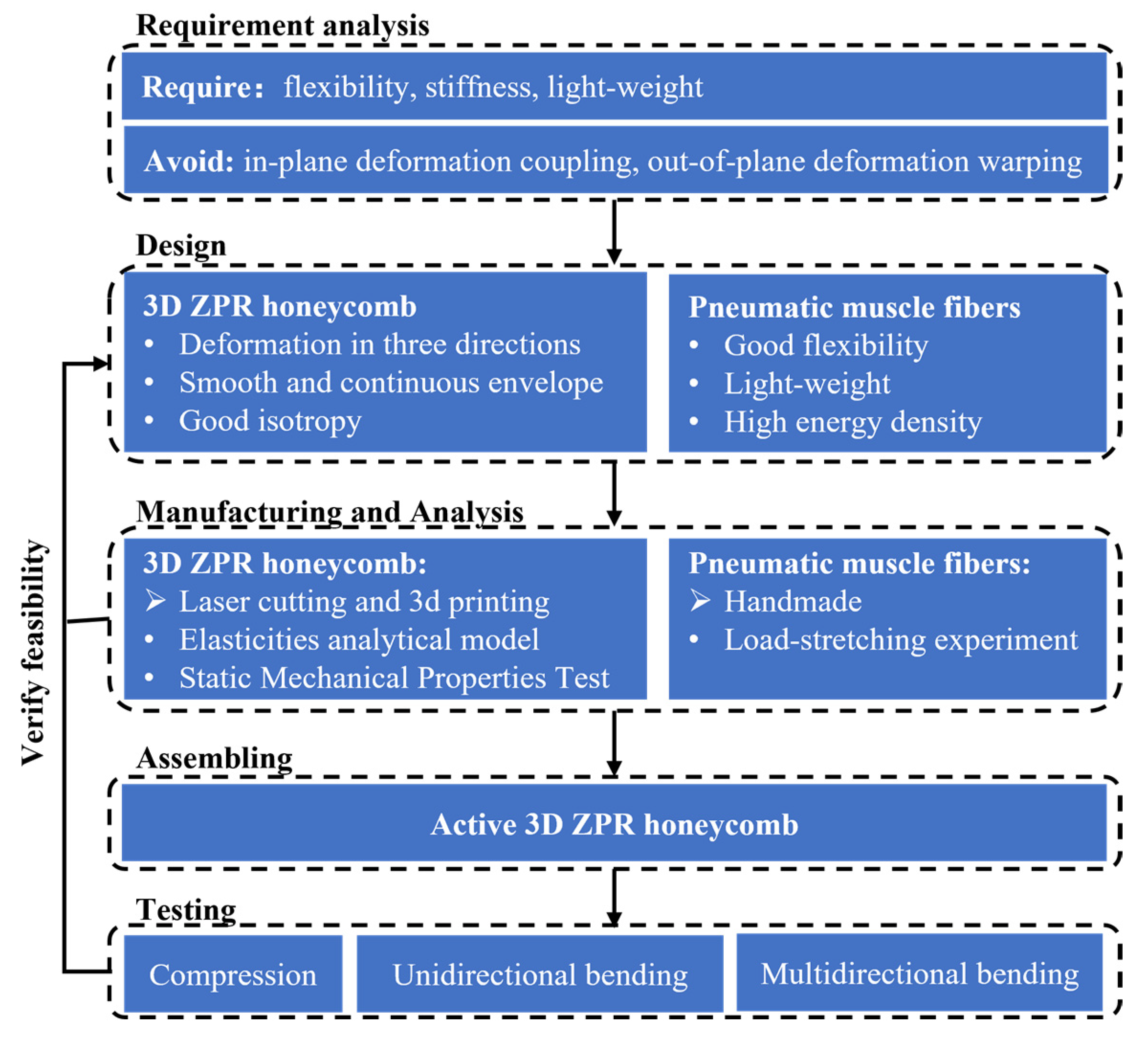
:1. Introduction
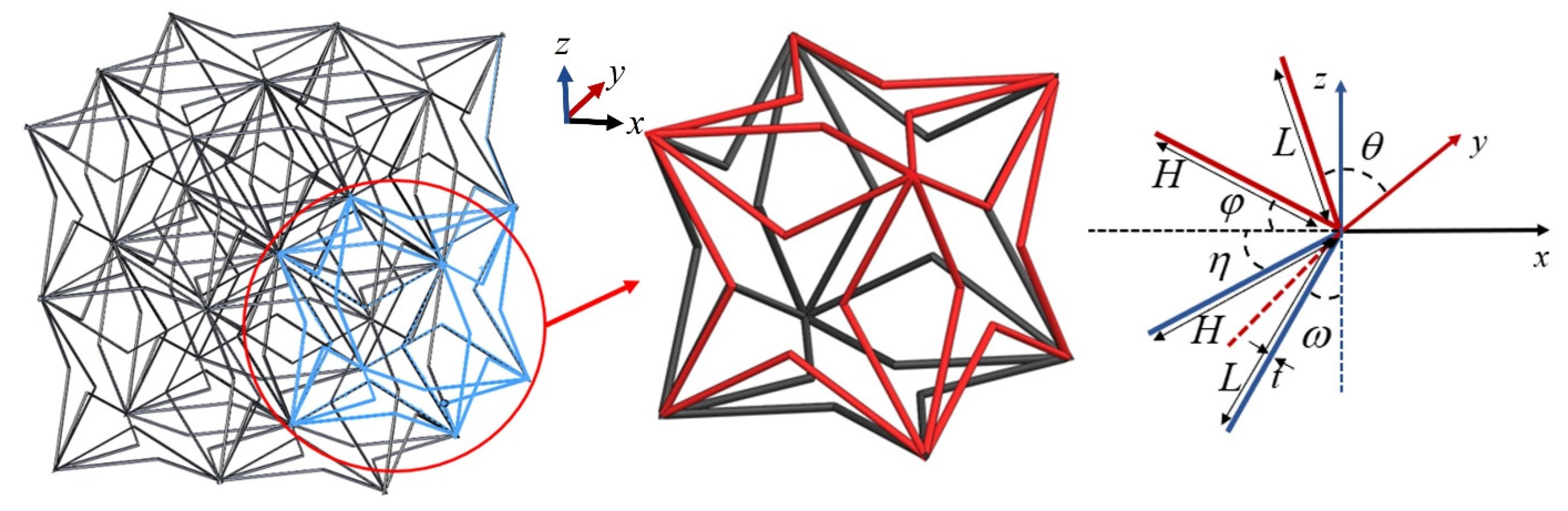
2. 3D ZPR Honeycomb Design
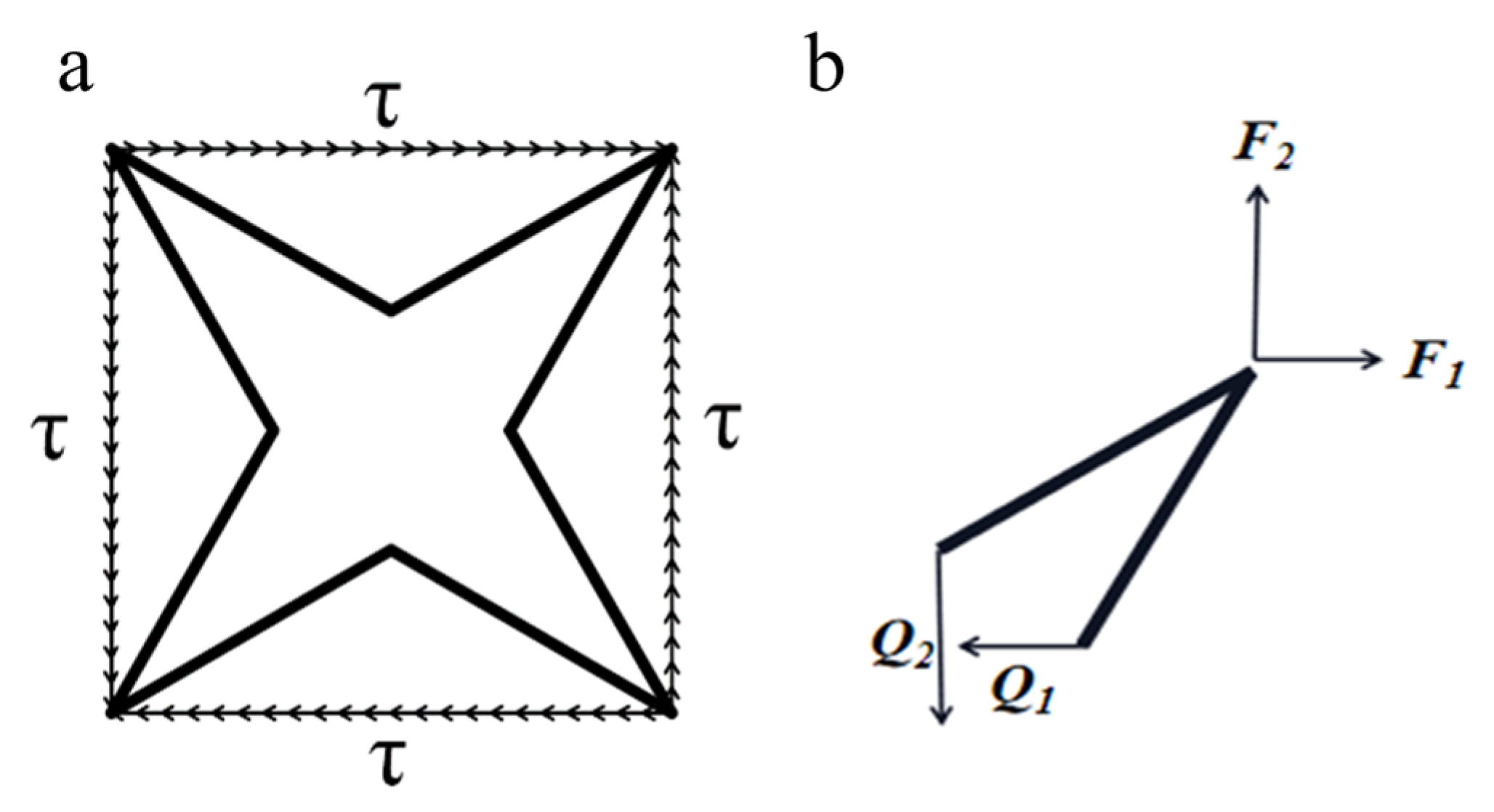
3. Elasticities Analytical Model
4. Static Mechanical Properties Test
4.1. Young’s Modulus Test
4.2. Poisson’s Ratio Test
4.3. 3D ZPR Honeycomb Compression Test
5. Design and Test of Deformation Driving Method for 3D ZPR Honeycomb
5.1. Active 3D ZPR Honeycomb Design
5.2. Pneumatic Muscle Fiber Actuation Testing
5.3. Compression Deformation
5.4. Unidirectional Bending Deformation
5.5. Multidirectional Bending Deformation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| 3D | Three-dimensional |
| A | Section area of inertia of cell wall |
| b | Wall Heights |
| Es | Young’s modulus of raw materials used to make honeycomb structures |
| Ex | Equivalent elastic modulus in the x-direction |
| Ex/Es | Nondimensional elastic modulus in the x-direction |
| Ey | Equivalent elastic modulus in the y-direction |
| Ey/Es | Nondimensional elastic modulus in the y-direction |
| Ez | Equivalent elastic modulus in the z-direction |
| Ez/Es | Nondimensional elastic modulus in the z-direction |
| Gxy | Shear modulus of x-o-y plane |
| H | Wall length in the x-o-y plane |
| I | Section moment of inertia of cell wall |
| L | Wall length in the x-o-y plane |
| LA−B | Length between points A and B |
| Lxi | Original lengths between the marker points in the x-direction |
| L’xi | Lengths between the marker points in the x-direction |
| Lyi | Original lengths between the marker points in the y-direction |
| L’yi | Lengths between the marker points in the y-direction |
| M1 | Bending moment at endpoint 1 |
| M2 | Bending moment at endpoint 1 |
| N | Force of cell wall along the x-direction |
| N1 | Force parallel to cell wall at endpoint 1 |
| N2 | Force perpendicular to cell wall at endpoint 1 |
| NA−B | Number of pixels between points A and B |
| NPR | Negative Poisson’s ratios |
| PLC | Programmable Logic Controller |
| PPR | Positive Poisson’s ratios |
| SLS | Selective Laser Sintering technology |
| t | Wall thickness |
| ZPR | Zero Poisson’s Ratio |
| α | Nondimensional length, α = H/L |
| β | Nondimensional length, α = t/L |
| γ | Nondimensional length, α = b/L |
| γxy | Shear strain in the x-o-y plane |
| δx | Deflection under σx |
| Δx | Displacements in the x-direction at wall endpoints |
| Δy | Displacements in the y-direction at wall endpoints |
| εx | Normal strain in the x-direction |
| εy | Normal strain in the y-direction |
| η | Wall slope angle in the x-o-z plane |
| θ | Wall slope angle in the x-o-y plane |
| κ | Shear stress shape coefficient of the rectangular section |
| νxy | Poisson’s ratio in the x-o-y plane |
| σx | Stress in the x direction |
| τ | Pure shear stress |
| φ | Wall slope angle in the x-o-y plane |
| ω | Wall slope angle in the x-o-z plane |
References
- Ajaj, R.M.; Parancheerivilakkathil, M.S.; Amoozgar, M.; Friswell, M.I.; Cantwell, W.J. Recent developments in the aeroelasticity of morphing aircraft. Prog. Aerosp. Sci. 2021, 120, 100682. [Google Scholar]
- Weisshaar, T.A. Morphing Aircraft Systems: Historical Perspectives and Future Challenges. J. Aircr. 2013, 50, 337–353. [Google Scholar] [CrossRef]
- Sun, J.; Guan, Q.; Liu, Y.; Leng, J. Morphing aircraft based on smart materials and structures: A state-of-the-art review. J. Intell. Mater. Syst. Struct. 2016, 27, 2289–2312. [Google Scholar] [CrossRef]
- Jha, A.K.; Kudva, J.N. Morphing aircraft concepts, classifications, and challenges. In Proceedings of the Smart Structures and Materials 2004: Industrial and Commercial Applications of Smart Structures Technologies, San Diego, CA, USA, 14–18 March 2004; Volume 5388, pp. 213–224. [Google Scholar]
- Sofla, A.; Meguid, S.; Tan, K.; Yeo, W. Shape morphing of aircraft wing: Status and challenges. Mater. Des. 2010, 31, 1284–1292. [Google Scholar] [CrossRef]
- Barbarino, S.; Bilgen, O.; Ajaj, R.M.; Friswell, M.I.; Inman, D.J. A review of morphing aircraft. J. Intell. Mater. Syst. Struct. 2011, 22, 823–877. [Google Scholar] [CrossRef]
- Chu, L.; Li, Q.; Gu, F.; Du, X.; He, Y.; Deng, Y. Design, modeling, and control of morphing aircraft: A review. Chin. J. Aeronaut. 2022, 35, 220–246. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Olympio, K.R.; Gandhi, F. Flexible skins for morphing aircraft using cellular honeycomb cores. J. Intell. Mater. Syst. Struct. 2009, 21, 1719–1735. [Google Scholar] [CrossRef]
- Masters, I.; Evans, K. Models for the elastic deformation of honeycombs. Compos. Struct. 1996, 35, 403–422. [Google Scholar] [CrossRef]
- Bitzer, T. Honeycomb Technology: Materials, Design, Manufacturing, Applications and Testing; Springer Science & Business Media: Berlin, Germany, 1997. [Google Scholar]
- Almgren, R.F. An isotropic three-dimensional structure with Poisson’s ratio = −1. J. Elast. 1985, 15, 427–430. [Google Scholar]
- Lira, C.; Innocenti, P.; Scarpa, F. Transverse elastic shear of auxetic multi re-entrant honeycombs. Compos. Struct. 2009, 90, 314–322. [Google Scholar] [CrossRef]
- Chen, Y.; Scarpa, F.; Liu, Y.; Leng, J. Elasticity of anti-tetrachiral anisotropic lattices. Int. J. Solids Struct. 2013, 50, 996–1004. [Google Scholar] [CrossRef] [Green Version]
- Lorato, A.; Innocenti, P.; Scarpa, F.; Alderson, A.; Alderson, K.; Zied, K.; Ravirala, N.; Miller, W.; Smith, C.; Evans, K. The transverse elastic properties of chiral honeycombs. Compos. Sci. Technol. 2010, 70, 1057–1063. [Google Scholar] [CrossRef]
- Airoldi, A.; Bettini, P.; Panichelli, P.; Sala, G. Chiral topologies for composite morphing structures—Part II: Novel configurations and technological processes. Phys. Status Solidi B Basic Solid State Phys. 2015, 252, 1446–1454. [Google Scholar] [CrossRef]
- Theocaris, P.; Stavroulakis, G.; Panagiotopoulos, P. Negative Poisson’s ratios in composites with star-shaped inclusions: A numerical homogenization approach. Arch. Appl. Mech. 1997, 67, 274–286. [Google Scholar] [CrossRef]
- Duan, S.; Xi, L.; Wen, W.; Fang, D. A novel design method for 3D positive and negative Poisson’s ratio material based on tension-twist coupling effects. Compos. Struct. 2020, 236, 111899. [Google Scholar] [CrossRef]
- Larsen, U.D.; Signund, O.; Bouwsta, S. Design and fabrication of compliant micromechanisms and structures with negative Poisson’s ratio. J. Microelectromechanical Syst. 1997, 6, 99–106. [Google Scholar] [CrossRef] [Green Version]
- Olympio, K.R.; Gandhi, F. Zero Poisson’s ratio cellular honeycombs for flex skins undergoing one-dimensional morphing. J. Intell. Mater. Syst. Struct. 2010, 21, 1737–1753. [Google Scholar] [CrossRef]
- Alderson, A.; Alderson, K.L.; Chirima, G.; Ravirala, N.; Zied, K.M. The in-plane linear elastic constants and out-of-plane bending of 3-coordinated ligament and cylinder-ligament honeycombs. Compos. Sci. Technol. 2010, 70, 1034–1041. [Google Scholar] [CrossRef] [Green Version]
- Attard, D.; Grima, J.N. Modelling of hexagonal honeycombs exhibiting zero Poisson’s ratio. Phys. Status Solidi 2011, 248, 52–59. [Google Scholar] [CrossRef]
- Virk, K.; Monti, A.; Trehard, T.; Marsh, M.; Hazra, K.; Boba, K.; Remillat, C.; Scarpa, F.; Farrow, I. SILICOMB PEEK Kirigami cellular structures: Mechanical response and energy dissipation through zero and negative stiffness. Smart Mater. Struct. 2013, 22, 084014. [Google Scholar] [CrossRef]
- Liu, W.; Li, H.; Yang, Z.; Zhang, J.; Xiong, C. Mechanics of a novel cellular structure for morphing applications. Aerosp. Sci. Technol. 2019, 95, 105479. [Google Scholar] [CrossRef]
- Liu, W.; Li, H.; Zhang, J.; Bai, Y. In-plane mechanics of a novel cellular structure for multiple morphing applications. Compos. Struct. 2019, 207, 598–611. [Google Scholar] [CrossRef]
- Gong, X.; Huang, J.; Scarpa, F.; Liu, Y.; Leng, J. Zero Poisson’s ratio cellular structure for two-dimensional morphing applications. Compos. Struct. 2015, 134, 384–392. [Google Scholar] [CrossRef] [Green Version]
- Bubert, E.A.; Woods, B.K.; Lee, K.; Kothera, C.S.; Wereley, N.M. Design and fabrication of a passive 1D morphing aircraft skin. J. Intell. Mater. Syst. Struct. 2010, 21, 1699–1717. [Google Scholar] [CrossRef]
- Farrokhabadi, A.; Ashrafian, M.M.; Fotouhi, M. Design and characterization of an orthotropic accordion cellular honeycomb as one-dimensional morphing structures with enhanced properties. J. Sandw. Struct. Mater. 2022, 24, 1726–1745. [Google Scholar] [CrossRef]
- Bishay, P.L.; Burg, E.; Akinwunmi, A.; Phan, R.; Sepulveda, K. Development of a New Span-Morphing Wing Core Design. Designs 2019, 3, 12. [Google Scholar] [CrossRef] [Green Version]
- Lira, C.; Scarpa, F.; Olszewska, M.; Celuch, M. The SILICOMB cellular structure: Mechanical and dielectric properties. Phys. Status Solidi 2009, 246, 2055–2062. [Google Scholar] [CrossRef]
- Naghavi Zadeh, M.; Dayyani, I.; Yasaee, M. Fish Cells, a new zero Poisson’s ratio metamaterial-Part I: Design and experiment. J. Intell. Mater. Syst. Struct. 2020, 31, 1617–1637. [Google Scholar] [CrossRef]
- Liu, W.; Yang, Z.; Du, S.; Li, H.; Zhang, Q. Theoretical, numerical and experimental study on the in-plane elastic behavior of a 2D chiral cellular structure. Compos. Struct. 2022, 296, 115889. [Google Scholar] [CrossRef]
- Liu, W.; Jiang, H.; Chen, Y. 3D Programmable Metamaterials Based on Reconfigurable Mechanism Modules. Adv. Funct. Mater. 2022, 32, 2109865. [Google Scholar] [CrossRef]
- Liu, W.; Zhu, H.; Zhou, S.; Bai, Y.; Wang, Y.; Zhao, C. In-plane corrugated cosine honeycomb for 1D morphing skin and its application on variable camber wing. Chin. J. Aeronaut. 2013, 26, 935–942. [Google Scholar] [CrossRef] [Green Version]
- Vocke, R.D.; Kothera, C.S.; Woods, B.K.; Wereley, N.M. Development and Testing of a Span-Extending Morphing Wing. J. Intell. Mater. Syst. Struct. 2011, 22, 879–890. [Google Scholar] [CrossRef]
- Liu, W.; Li, H.; Zhang, J.; Gong, X.; Wang, Y.; Ge, X. Tensile and shear properties of star-shaped cellular lattice structure. Mech. Adv. Mater. Struct. 2021, 28, 2605–2617. [Google Scholar] [CrossRef]
- Gao, Y.-K. Auxetic metamaterials and structures. Cailiao Gongcheng J. Mater. Eng. 2021, 49, 38–47. [Google Scholar]
- Ma, P.; Chang, Y.; Boakye, A.; Jiang, G. Review on the knitted structures with auxetic effect. J. Text. Inst. 2016, 108, 947–961. [Google Scholar] [CrossRef]
- Mir, M.; Ali, M.N.; Sami, J.; Ansari, U. Review of Mechanics and Applications of Auxetic Structures. Adv. Mater. Sci. Eng. 2014, 2014, 753496. [Google Scholar] [CrossRef] [Green Version]
- Ren, X.; Shen, J.; Phuong, T.; Ngo, T.D.; Xie, Y.M. Design and characterisation of a tuneable 3D buckling-induced auxetic metamaterial. Mater. Des. 2018, 139, 336–342. [Google Scholar] [CrossRef]
- Xue, Y.; Wang, X.; Wang, W.; Zhong, X.; Han, F. Compressive property of Al-based auxetic lattice structures fabricated by 3-D printing combined with investment casting. Mater. Sci. Eng. A Struct. Mater. Prop. Microstruct. Process. 2018, 722, 255–262. [Google Scholar] [CrossRef]
- Li, D.; Ma, J.; Dong, L.; Lakes, R.S. Three-Dimensional Stiff Cellular Structures With Negative Poisson’s Ratio. Phys. Status Solidi B Basic Solid State Phys. 2017, 254, 1600785. [Google Scholar] [CrossRef]
- Lei, M.; Hong, W.; Zhao, Z.; Hamel, C.; Chen, M.; Lu, H.; Qi, H.J. 3D Printing of Auxetic Metamaterials with Digitally Reprogrammable Shape. Acs Appl. Mater. Interfaces 2019, 11, 22768–22776. [Google Scholar] [CrossRef]
- Feng, N.; Liu, L.; Liu, Y.; Leng, J. A bio-inspired, active morphing skin for camber morphing structures. Smart Mater. Struct. 2015, 24, 035023. [Google Scholar] [CrossRef]


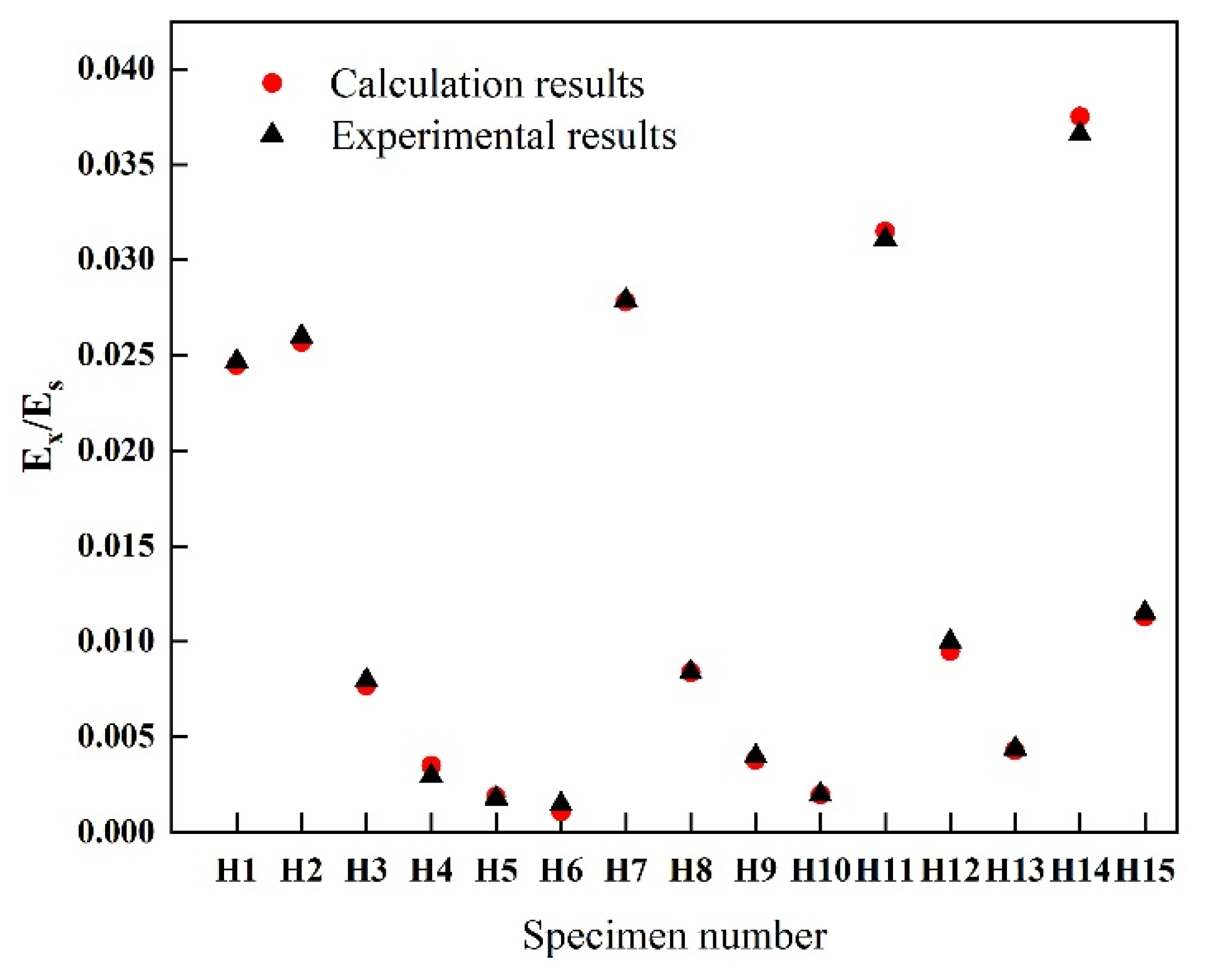
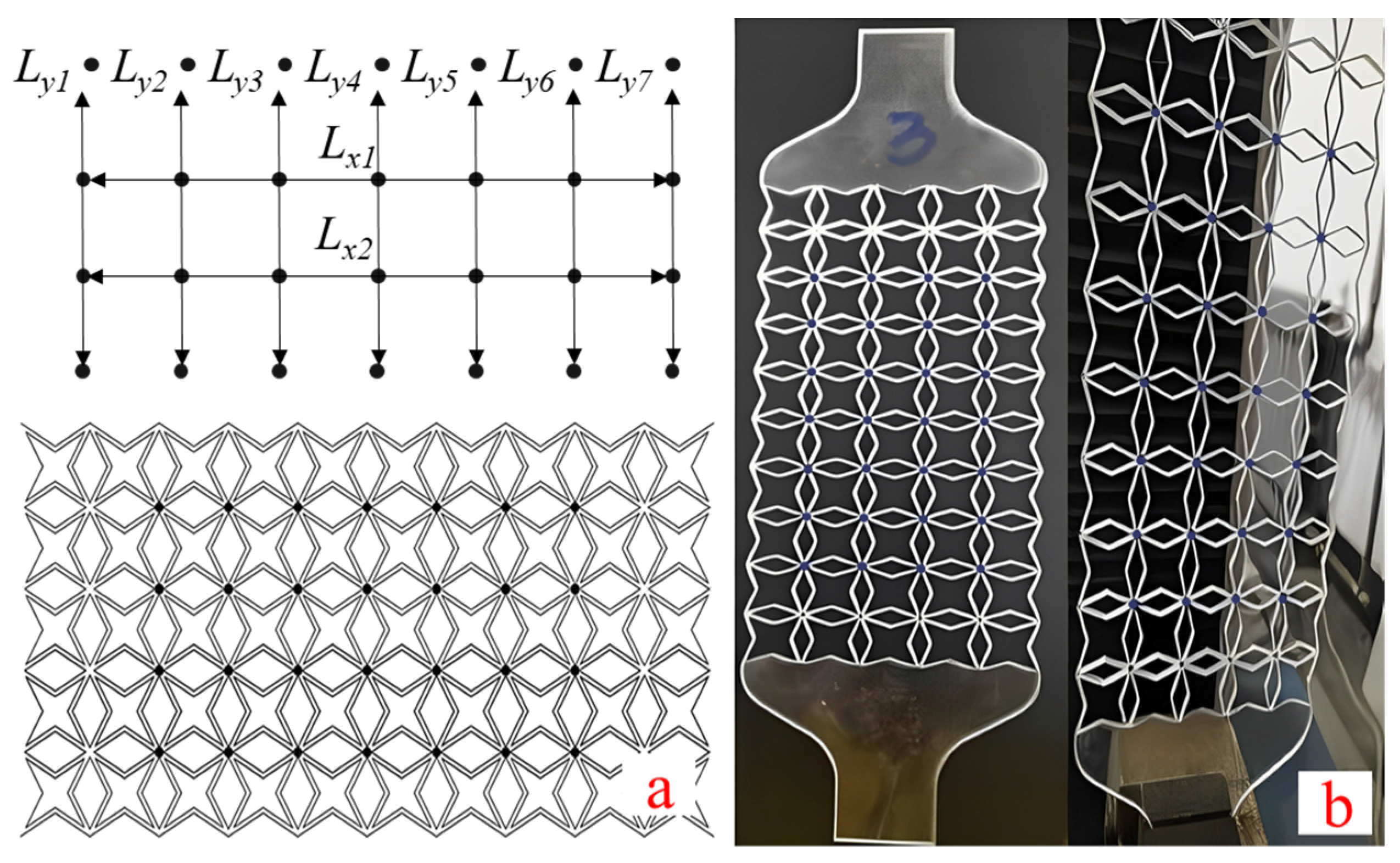
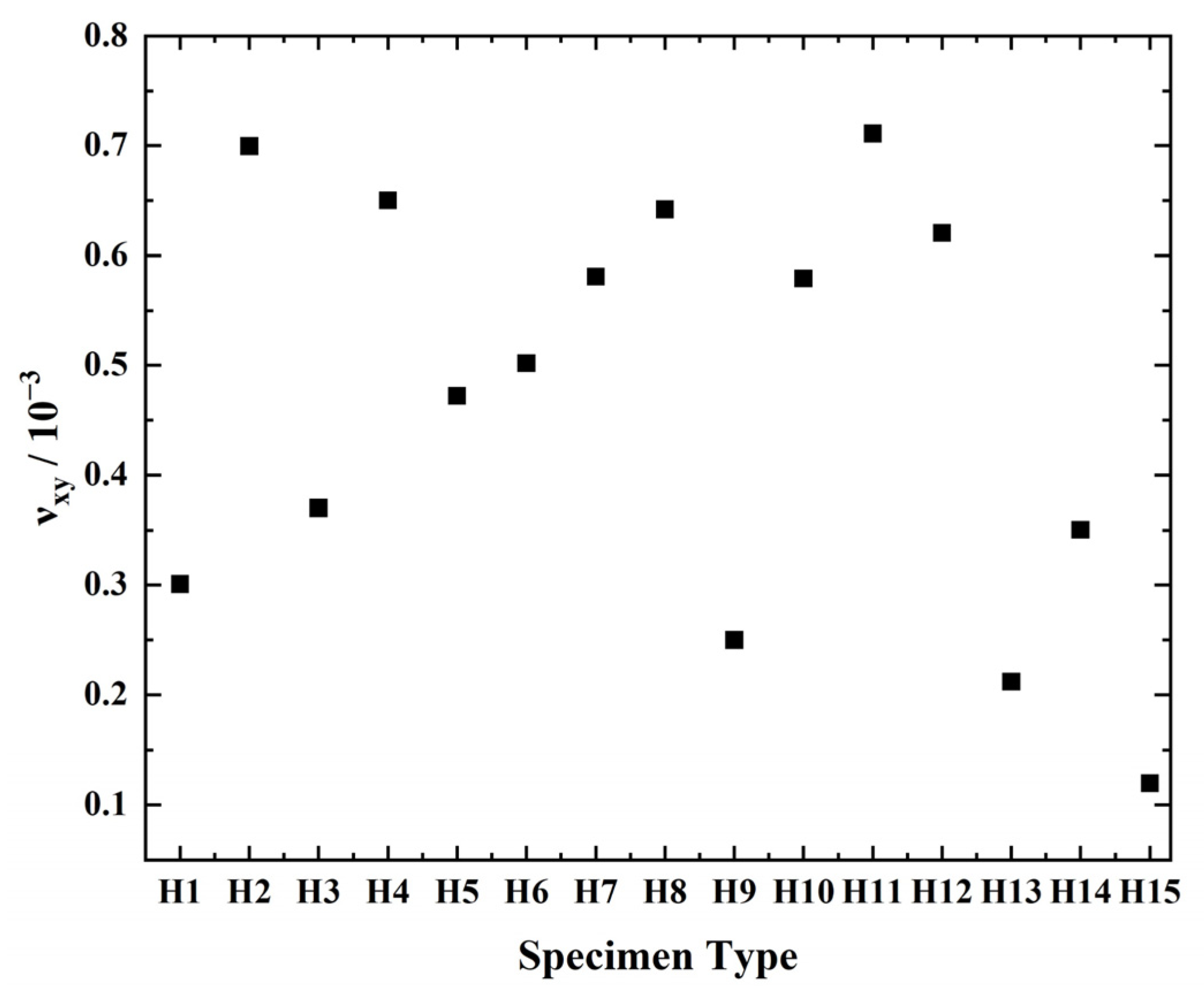



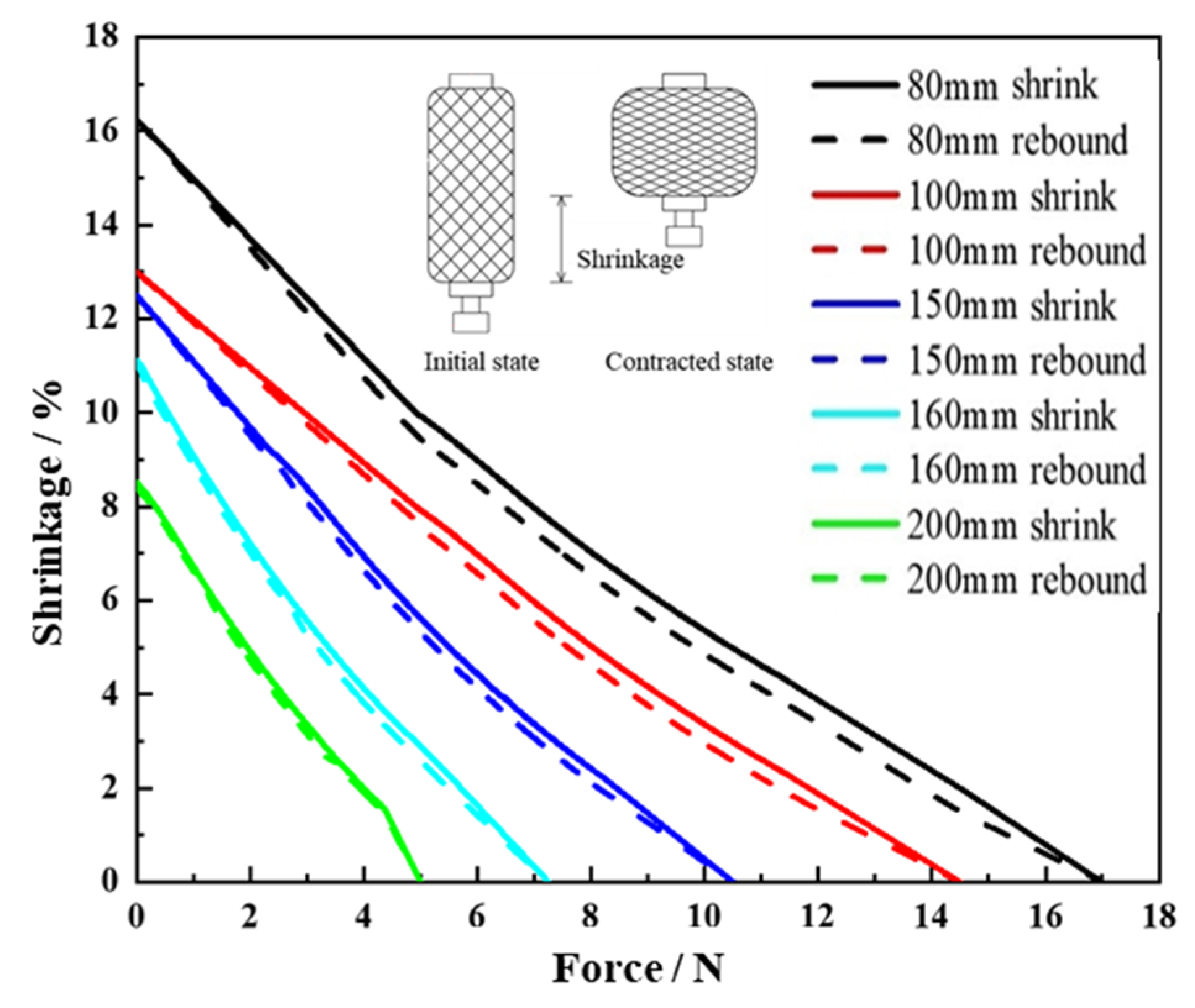



| No. | H1 | H2 | H3 | H4 | H5 | H6 | H7 | H8 | H9 | H10 | H11 | H12 | H13 | H14 | H15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| θ | 10 | 20 | 20 | 20 | 20 | 20 | 30 | 30 | 30 | 30 | 40 | 40 | 40 | 50 | 50 |
| φ | 10 | 10 | 20 | 30 | 40 | 50 | 10 | 20 | 30 | 40 | 10 | 20 | 30 | 10 | 20 |
| Specimen No. | Specimen Size (mm) | Experiment (MPa) | Theory (MPa) | Error (%) | |||
|---|---|---|---|---|---|---|---|
| ω (°) | η (°) | H (mm) | L (mm) | ||||
| R1 | 10 | 30 | 17 | 17 | 3.102 | 3.175 | 2.35 |
| R2 | 20 | 30 | 17 | 17 | 0.891 | 0.919 | 3.14 |
| R3 | 30 | 30 | 17 | 17 | 0.434 | 0.41 | 5.53 |
| R4 | 40 | 30 | 17 | 17 | 0.279 | 0.222 | 20.43 |
| Program | Prediction (°) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | Test (°) | Error (°) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| A1 | −45 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | −44 | −1 |
| A2 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 2 | 1.5 |
| A3 | 45 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 47 | 2 |
| A4 | 90 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 88 | −2 |
| A5 | 135 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 136 | 1 |
| A6 | 180 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 178 | −2 |
| A7 | 225 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 223 | −2.5 |
| A8 | 270 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 269 | −1.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, X.; Ren, C.; Sun, J.; Zhang, P.; Du, L.; Xie, F. 3D Zero Poisson’s Ratio Honeycomb Structure for Morphing Wing Applications. Biomimetics 2022, 7, 198. https://doi.org/10.3390/biomimetics7040198
Gong X, Ren C, Sun J, Zhang P, Du L, Xie F. 3D Zero Poisson’s Ratio Honeycomb Structure for Morphing Wing Applications. Biomimetics. 2022; 7(4):198. https://doi.org/10.3390/biomimetics7040198
Chicago/Turabian StyleGong, Xiaobo, Chengwei Ren, Jian Sun, Peiru Zhang, Lei Du, and Fang Xie. 2022. "3D Zero Poisson’s Ratio Honeycomb Structure for Morphing Wing Applications" Biomimetics 7, no. 4: 198. https://doi.org/10.3390/biomimetics7040198





