Structure and Frictional Properties of the Leg Joint of the Beetle Pachnoda marginata (Scarabaeidae, Cetoniinae) as an Inspiration for Technical Joints
Abstract
1. Introduction
- The coefficient of sliding friction µk has a dependence on the real contact area for a low contact stress;
- There is a directional dependence of the μk that is given by the microstructure with an asymmetric cross-section.
2. Materials and Methods
2.1. Sample Preparation of Insects
2.2. Scanning Electron Microscopy of Insects
2.3. Confocal Laser Scanning Microscopy
2.4. Friction Measurements of Beetle Joints Using Nanotribometer
2.5. Friction Measurements of Bioinspired Joints Using Tribometer
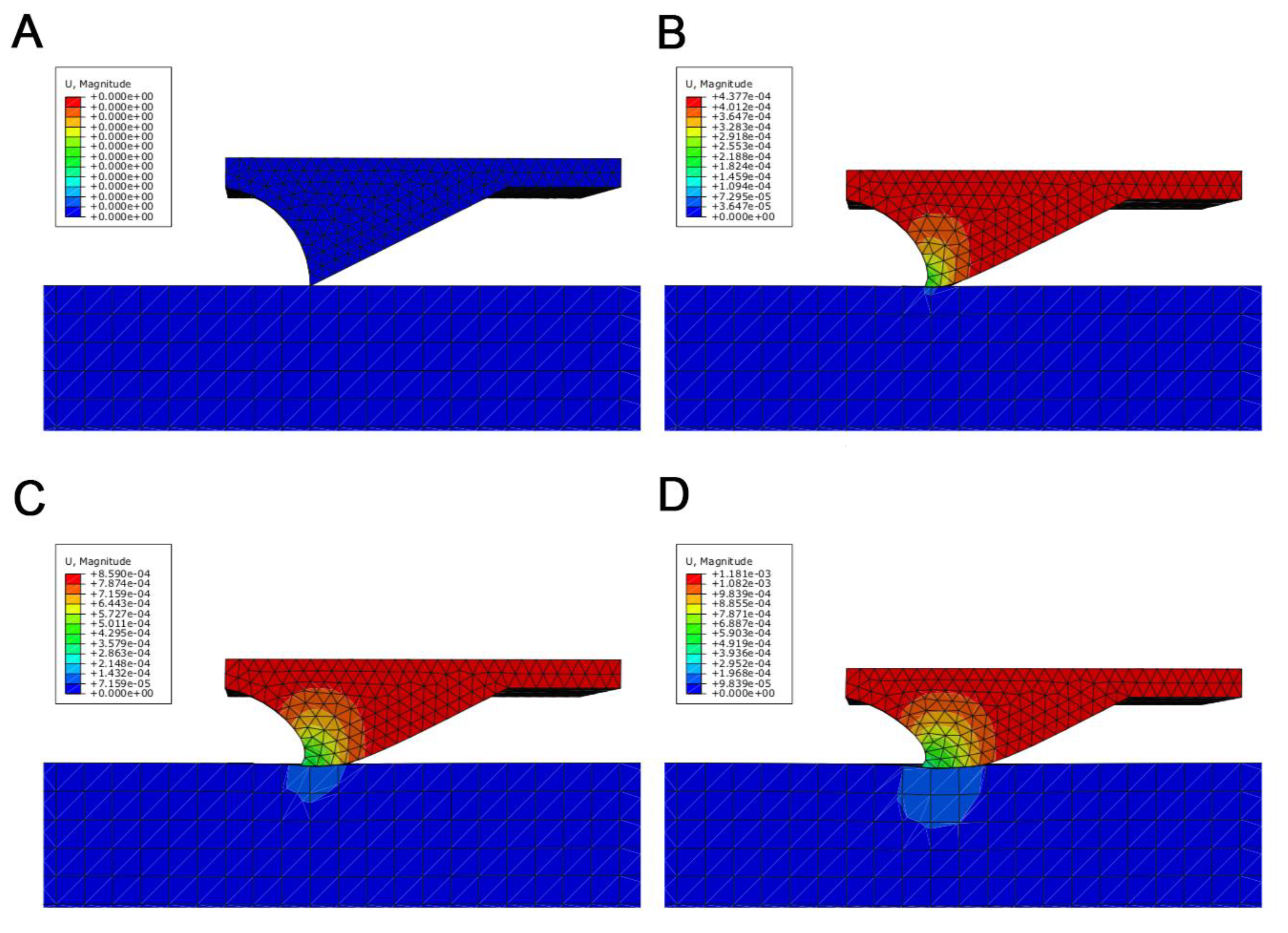
2.6. Finite Element Analysis
2.7. Preparation of Bioinspired Surfaces Using Selective Laser Melting
2.8. Statistical Analysis
3. Results
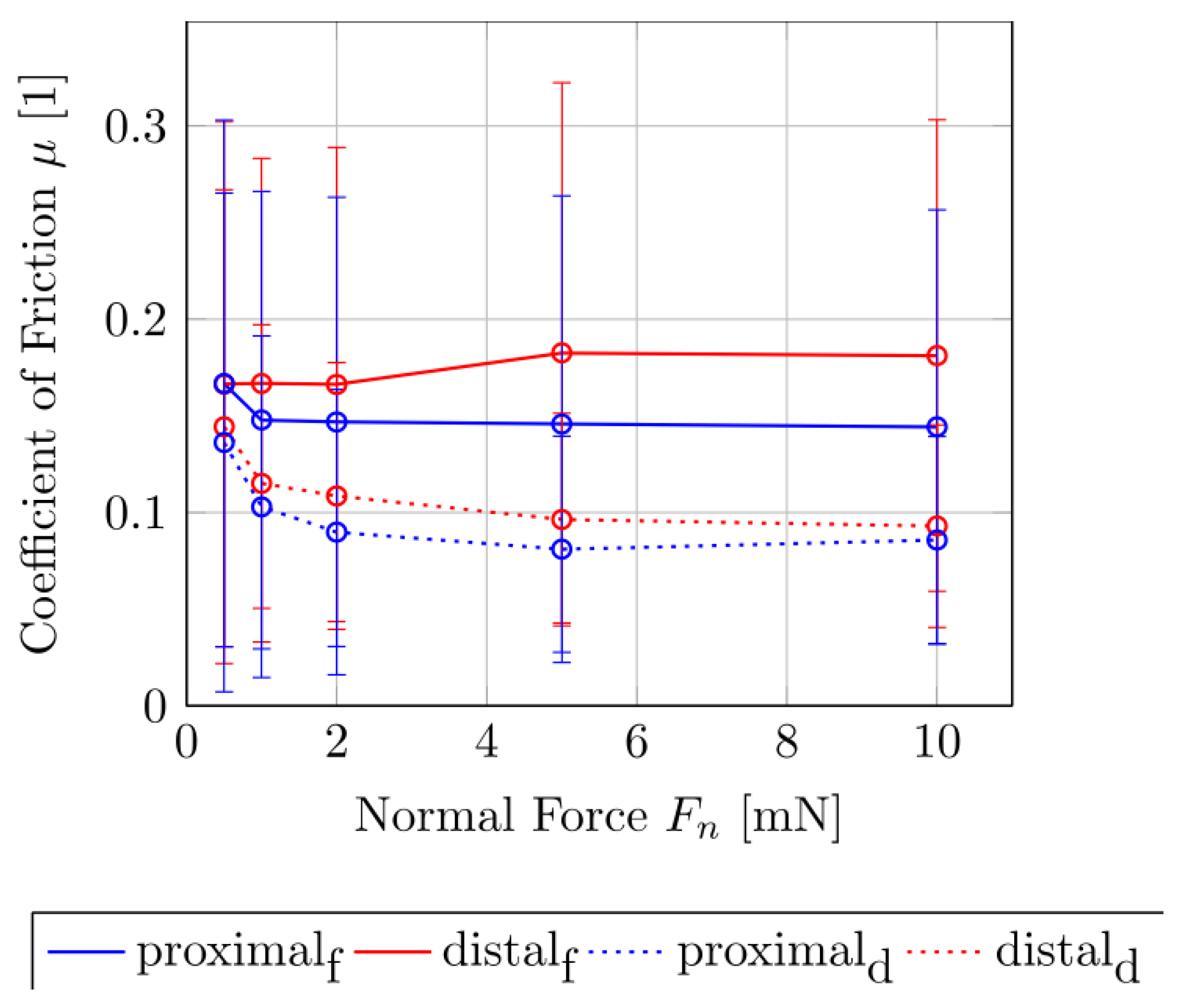
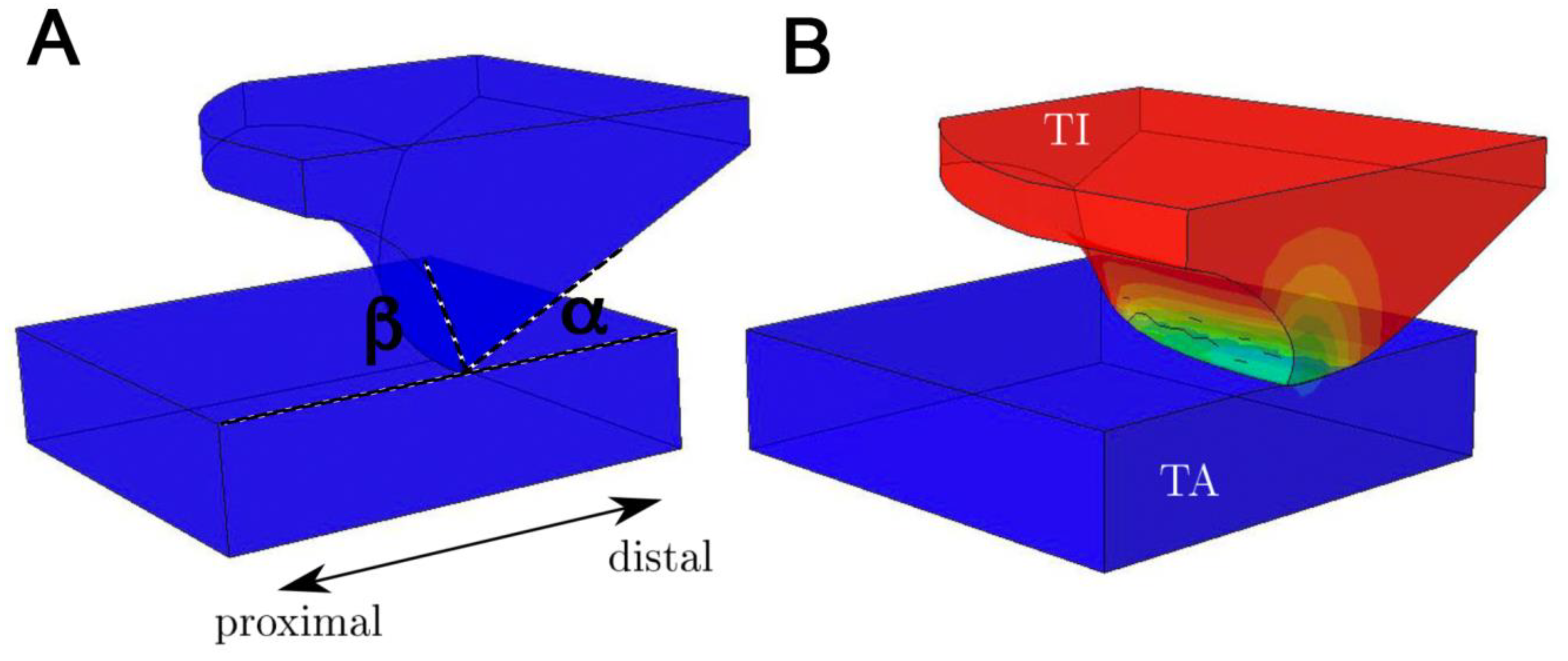
3.1. Results of Biological Contact Pair
3.2. Results of Technical Contact Pair
4. Discussion
4.1. Biological Tribo System
- The microfibrils are situated within planes parallelly orientated to the cuticle surface;
- Within one layer, all chitin fibers run parallel to the surface and to each other;
- Microfibrils situated in successive levels are usually rotated relative to each other at an angle that can vary or remain constant in different cuticles;
- The number of layers creating full rotation (180°) are called lamella. The thickness of lamella varies depending on the thickness of the microfibrils and the angle of rotation.
4.2. Artificial Tribo System
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Rabinowicz, E. Friction and Wear of Materials, 2nd ed.; Wiley: New York, NY, USA, 1995. [Google Scholar]
- Scherge, M.; Gorb, S.N. Biological Micro- and Nanotribology; Springer: Berlin, Germany, 2001. [Google Scholar]
- Bowden, F.P.; Tabor, D. The Friction and Lubrication of Solids; Clarendon Press: Oxford, UK, 1950. [Google Scholar]
- Persson, B.N. Sliding Friction: Physical Principles and Applications; Springer: Berlin, Germany, 2000; Volume 1. [Google Scholar]
- Popov, V.L. Contact Mechanics and Friction; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Persson, B.N.J.; Kovalev, A.; Wasem, M.; Gnecco, E.; Gorb, S.N. Surface roughness of peeled adhesive tape: A mystery? EPL Europhys. Lett. 2010, 92, 46001. [Google Scholar] [CrossRef]
- Baum, M.J.; Heepe, L.; Fadeeva, E.; Gorb, S.N. Dry friction of microstructured polymer surfaces inspired by snake skin. Beilstein J. Nanotechnol. 2014, 5, 1091–1103. [Google Scholar] [CrossRef] [PubMed]
- Bhushan, B. Micro/nanotribology and materials characterization studies using scanning probe microscopy. In Springer Handbook of Nanotechnology; Springer: Berlin, Germany, 2004; pp. 497–541. [Google Scholar]
- Czichos, H. Tribology: A Systems Approach to the Science and Technology of Friction, Lubrication and Wear; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Tambe, N.S.; Bhushan, B. Scale dependence of micro/nano-friction and adhesion of mems/nems materials, coatings and lubricants. Nanotechnology 2004, 15, 1561. [Google Scholar] [CrossRef]
- Gorb, S.N. Attachment Devices of Insect Cuticle; Springer: Berlin, Germany, 2001. [Google Scholar]
- Dai, Z.; Gorb, S.N. Micro-structure and frictional characteristics of beetle’s joint. Sci. China Ser. G Phys. Mech. Astron. 2004, 47, 99–106. [Google Scholar] [CrossRef]
- Kheireddin, B.A.; Wiliams, T.C.; Akbulut, M. Tribological properties of femur-tibia articulation of lubber grasshopper. Tribol. Int. 2012, 50, 76–81. [Google Scholar] [CrossRef]
- Barbakadze, N.; Enders, S.; Gorb, S.; Arzt, E. Local mechanical properties of the head articulation cuticle in the beetle Pachnoda marginata (Coleoptera, Scarabaeidae). J. Exp. Biol. 2006, 209, 722–730. [Google Scholar] [CrossRef]
- Hazel, J.; Stone, M.; Grace, M.S.; Tsukruk, V.V. Nanoscale design of snake skin for reputation locomotions via friction anisotropy. J. Biomech. 1999, 32, 477–484. [Google Scholar] [CrossRef]
- Berthe, R.; Westhoff, G.; Bleckmann, H.; Gorb, S. Surface structure and frictional properties of the skin of the amazon tree boa Corallus hortulanus (Squamata, Boidae). J. Comp. Physiol. A 2009, 195, 311–318. [Google Scholar] [CrossRef]
- Baum, M.J.; Kovalev, A.E.; Michels, J.; Gorb, S.N. Anisotropic friction of the ventral scales in the snake lampropeltis getula californiae. Tribol. Lett. 2014, 54, 139–150. [Google Scholar] [CrossRef]
- Vagts, S.; Schlattmann, J.; Kovalev, A.; Gorb, S. The topology of the leg joints of the beetle Pachnoda marginata (Scarabaeidae, Cetoniinae) and its implication for the tribological properties. Biomimetics 2018, 3, 12. [Google Scholar] [CrossRef]
- Vagts, S.; Schlattmann, J. General systems theory in a horizontal and vertical action process for cross-disciplinary knowledge transfer. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition (IMECE 2013), San Diego, CA, USA, 15–21 November 2013. [Google Scholar] [CrossRef]
- Vagts, S.; Schlattmann, J.; Busshardt, P.; Kleinteich, T.; Gorb, S.N. The application of multi-body simulation approach in the kinematic analysis of beetle leg joints. Artif. Life Robot. 2017, 22, 412–420. [Google Scholar] [CrossRef]
- Altenbach, H.; Altenbach, J.; Rikards, R. Einführung in die Mechanik der Laminat- und Sandwichtragwerke; Deutscher Verlag Grundstoffindustrie: Stuttgart, Germany, 1996. [Google Scholar]
- Dai, Z.; Yang, Z. Macro-/micro-structures of elytra, mechanical properties of the biomaterial and the coupling strength between elytra in beetles. J. Bionic Eng. 2010, 7, 6–12. [Google Scholar] [CrossRef]
- Schulte, K. Faserverbundwerkstoffe mit Polymermatrix: Aufbau und Mechanische Eigenschaften; Deutsche Forschungsanstalt für Luft- und Raumfahrt, Institut für Werkstoff-Forschung: Braunschweig, Germany, 1992. [Google Scholar]
- Friedrich, K.; Schlarb, A.K. Tribology of Polymeric Nanocomposites: Friction and Wear of Bulk Materials and Coatings; Elsevier: Amsterdam, The Netherlands, 2011; Volume 55. [Google Scholar]
- Enders, S.; Barbakadze, N.; Gorb, S.N.; Arzt, E. Exploring biological surfaces by nanoindentation. J. Mater. Res. 2004, 19, 880–887. [Google Scholar] [CrossRef]
- Vincent, J.F.; Wegst, U.G. Design and mechanical properties of insect cuticle. Arthropod Struct. Dev. 2004, 33, 187–199. [Google Scholar] [CrossRef] [PubMed]
- Neville, A.C. Biology of the Arthropod Cuticle; Springer: Berlin, Germany, 2012; Volume 4. [Google Scholar]
- Fiedler, B. Hochleistungs-Faserverbundwerkstoffe mit Duroplastmatrix: Werkstoffe, Struktur, Eigenschaften, Modellierung; TuTech Innovation GmbH: Hamburg, Germany, 2009. [Google Scholar]
- Zhao, H.; Wie, J.J.; Copic, D.; Oliver, C.R.; Orbaek White, A.; Kim, S.; Hart, A.J. High-fidelity replica molding of glassy liquid crystalline polymer microstructures. ACS Appl. Mater. Interfaces 2016, 8, 8110–8117. [Google Scholar] [CrossRef] [PubMed]
- Altenbach, H. Kontinuumsmechanik: Einführung in die Materialunabhängigen und Materialabhängigen Gleichungen; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Barbakadze, N.; Enders, S.; Arzt, E.; Gorb, S.N. Friction properties of the head articulation in the beetle Pachnoda marginata (Coleoptera, Scarabaeidae). Biotribology 2019, 17, 30–39. [Google Scholar] [CrossRef]
- McNamara, M.E.; Briggs, D.E.; Orr, P.J.; Wedmann, S.; Noh, H.; Cao, H. Fossilized biophotonic nanostructures reveal the original colors of 47-million-year-old moths. PLoS Biol. 2011, 9, e1001200. [Google Scholar] [CrossRef]
- Marchetto, D.; Rota, A.; Calabri, L.; Gazzadi, G.C.; Menozzi, C.; Valeri, S. AFM investigation of tribological properties of nano-patterned silicon surface. Wear 2008, 265, 577–582. [Google Scholar] [CrossRef]
- Beutel, R.; Gorb, S. Ultrastructure of attachment specializations of hexapods (arthropoda): Evolutionary patterns inferred from a revised ordinal phylogeny. J. Zool. Syst. Evol. Res. 2001, 39, 177–207. [Google Scholar] [CrossRef]
- Greiner, C.; Schäfer, M.; Popp, U.; Gumbsch, P. Contact splitting and the effect of dimple depth on static friction of textured surfaces. ACS Appl. Mater. Interfaces 2014, 6, 7986–7990. [Google Scholar] [CrossRef]
- Bowden, F.P.; Tabor, D. The Friction and Lubrication of Solids; Clarendon Press: Oxford, UK, 1986. [Google Scholar]
- Filippov, A.; Gorb, S.N. Frictional-anisotropy-based systems in biology: Structural diversity and numerical model. Sci. Rep. 2013, 3, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Suh, N.P.; Mosleh, M.; Howard, P.S. Control of friction. Wear 1994, 175, 151–158. [Google Scholar] [CrossRef]
- Popov, V.; Filippov, A. Force of friction between fractal rough surface and elastomer. Tech. Phys. Lett. 2010, 36, 525–527. [Google Scholar] [CrossRef]
- Sondhauss, J.; Fuchs, H.; Schirmeisen, A. Frictional properties of a mesoscopic contact with engineered surface roughness. Tribol. Lett. 2011, 42, 319–324. [Google Scholar] [CrossRef]
- Baum, M.J.; Heepe, L.; Gorb, S.N. Friction behavior of a microstructured polymer surface inspired by snake skin. Beilstein J. Nanotechnol. 2014, 5, 83–97. [Google Scholar] [CrossRef] [PubMed]
- Tramsen, H.T.; Gorb, S.N.; Zhang, H.; Manoonpong, P.; Dai, Z.; Heepe, L. Inversion of friction anisotropy in a bio-inspired asymmetrically structured surface. J. R. Soc. Interface 2018, 15, 20170629. [Google Scholar] [CrossRef]
- Ma, S.; Scaraggi, M.; Yan, C.; Wang, X.; Gorb, S.N.; Dini, D.; Zhou, F. Bioinspired 3D printed locomotion devices based on anisotropic friction. Small 2018. [Google Scholar] [CrossRef]
- Ji, Z.; Yan, C.; Ma, S.; Gorb, S.N.; Jia, X.; Yu, B.; Wang, X.; Zhou, F. 3D printing of bioinspired topographically oriented surfaces with frictional anisotropy for directional driving. Tribol. Int. 2019, 132, 99–107. [Google Scholar] [CrossRef]


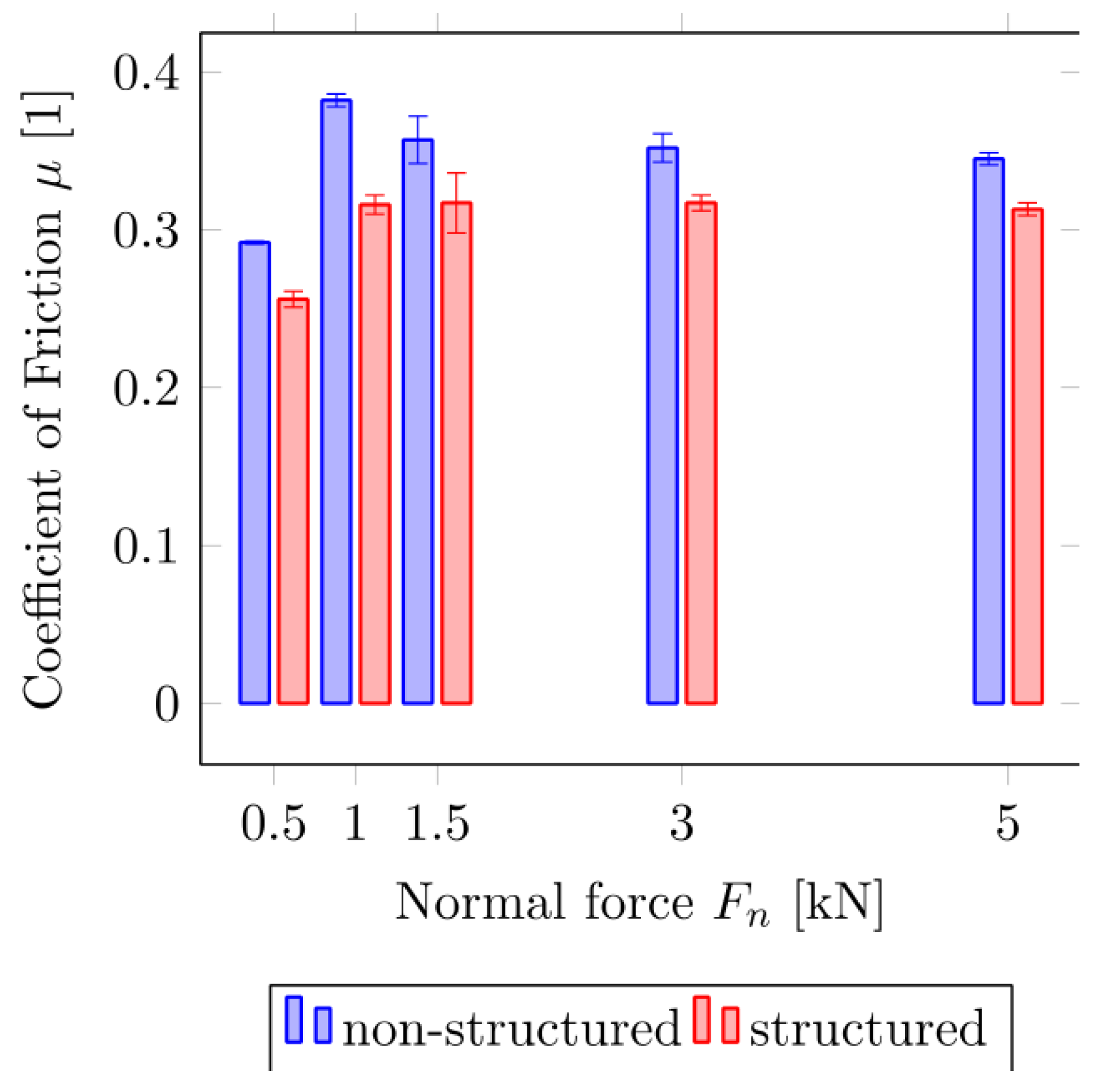
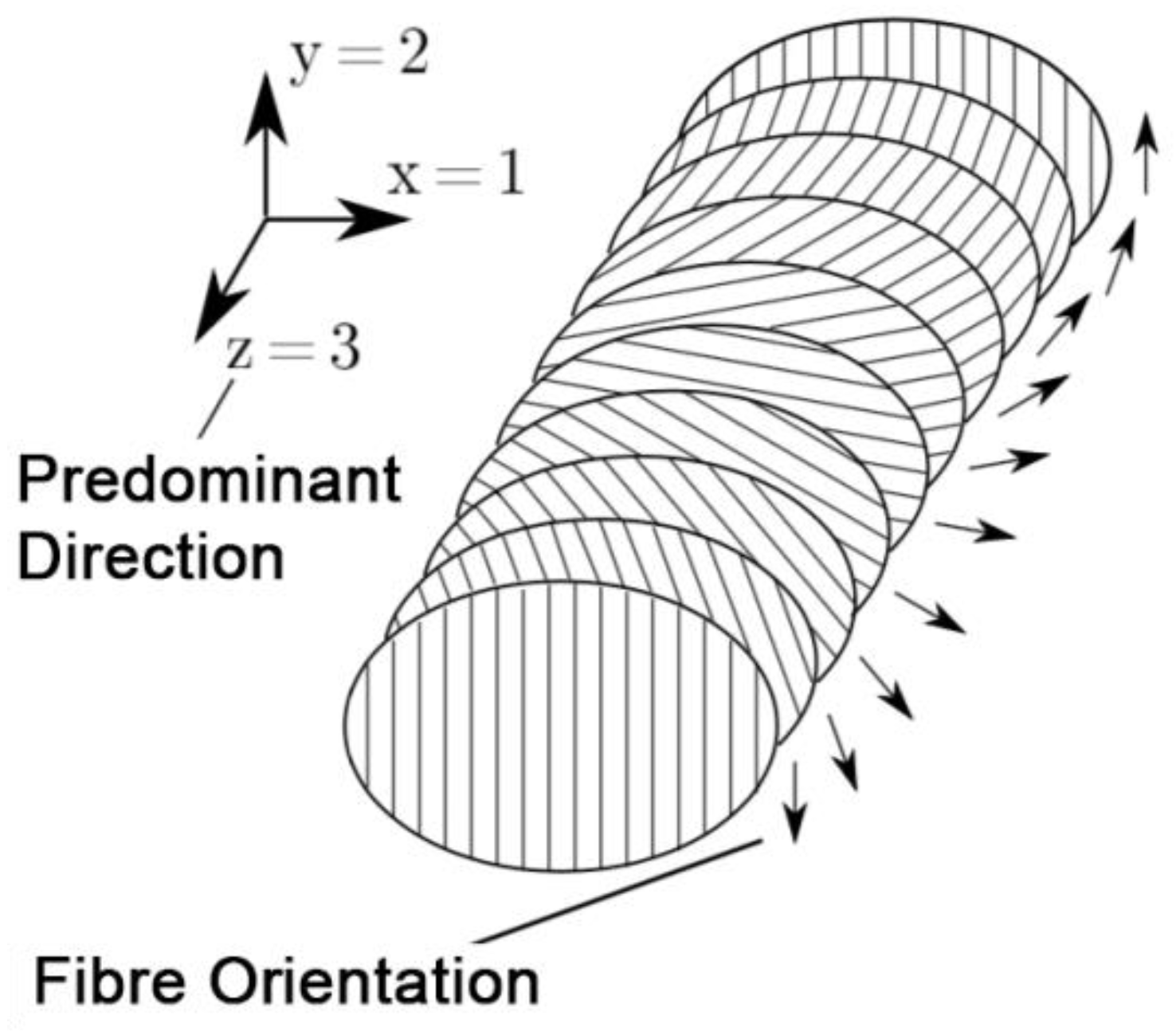
| Parameter | Tibia | Tarsus | Reference |
|---|---|---|---|
| E1 | 3090 MPa | 705 MPa | Equation 2 |
| E2 | 3090 MPa | 705 MPa | Equation 2 |
| E3 | 2060 MPa | 470 MPa | [18] |
| nu12 | 0.2 | 0.2 | [22] |
| nu13 | 0.3 | 0.3 | [23] |
| nu23 | 0.3 | 0.3 | [23] |
| G12 | 1287.5 MPa | 293.75 MPa | Equation 2 |
| G13 | 792 MPa | 181 MPa | Equation 2 |
| G23 | 792 MPa | 181 MPa | Equation 2 |
| Epi (µm) | Exo (µm) | Endo (µm) | Exo (µm) | |
|---|---|---|---|---|
| TId | 1.02 ± 0.17 | 12.14 ± 0.35 | 73.20 ± 3.40 | 7.72 ± 0.93 |
| TAp | 0.91 ± 0.13 | 11.81 to 22.49 | 56.37 ± 2.72 | n.a. |
| Length (µm) | Width (µm) | Height (µm) | |
|---|---|---|---|
| Pad | 127.65 ± 0.7 | 60.9 ± 0.6 | 96.17 ± 0.4 |
| Groove | - | 67.67 ± 0.8 | 96.17± 0.4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vagts, S.; Schlattmann, J.; Kovalev, A.; Gorb, S.N. Structure and Frictional Properties of the Leg Joint of the Beetle Pachnoda marginata (Scarabaeidae, Cetoniinae) as an Inspiration for Technical Joints. Biomimetics 2020, 5, 14. https://doi.org/10.3390/biomimetics5020014
Vagts S, Schlattmann J, Kovalev A, Gorb SN. Structure and Frictional Properties of the Leg Joint of the Beetle Pachnoda marginata (Scarabaeidae, Cetoniinae) as an Inspiration for Technical Joints. Biomimetics. 2020; 5(2):14. https://doi.org/10.3390/biomimetics5020014
Chicago/Turabian StyleVagts, Steffen, Josef Schlattmann, Alexander Kovalev, and Stanislav N. Gorb. 2020. "Structure and Frictional Properties of the Leg Joint of the Beetle Pachnoda marginata (Scarabaeidae, Cetoniinae) as an Inspiration for Technical Joints" Biomimetics 5, no. 2: 14. https://doi.org/10.3390/biomimetics5020014
APA StyleVagts, S., Schlattmann, J., Kovalev, A., & Gorb, S. N. (2020). Structure and Frictional Properties of the Leg Joint of the Beetle Pachnoda marginata (Scarabaeidae, Cetoniinae) as an Inspiration for Technical Joints. Biomimetics, 5(2), 14. https://doi.org/10.3390/biomimetics5020014






