Imaging with Polarized Neutrons
Abstract
:1. Introduction
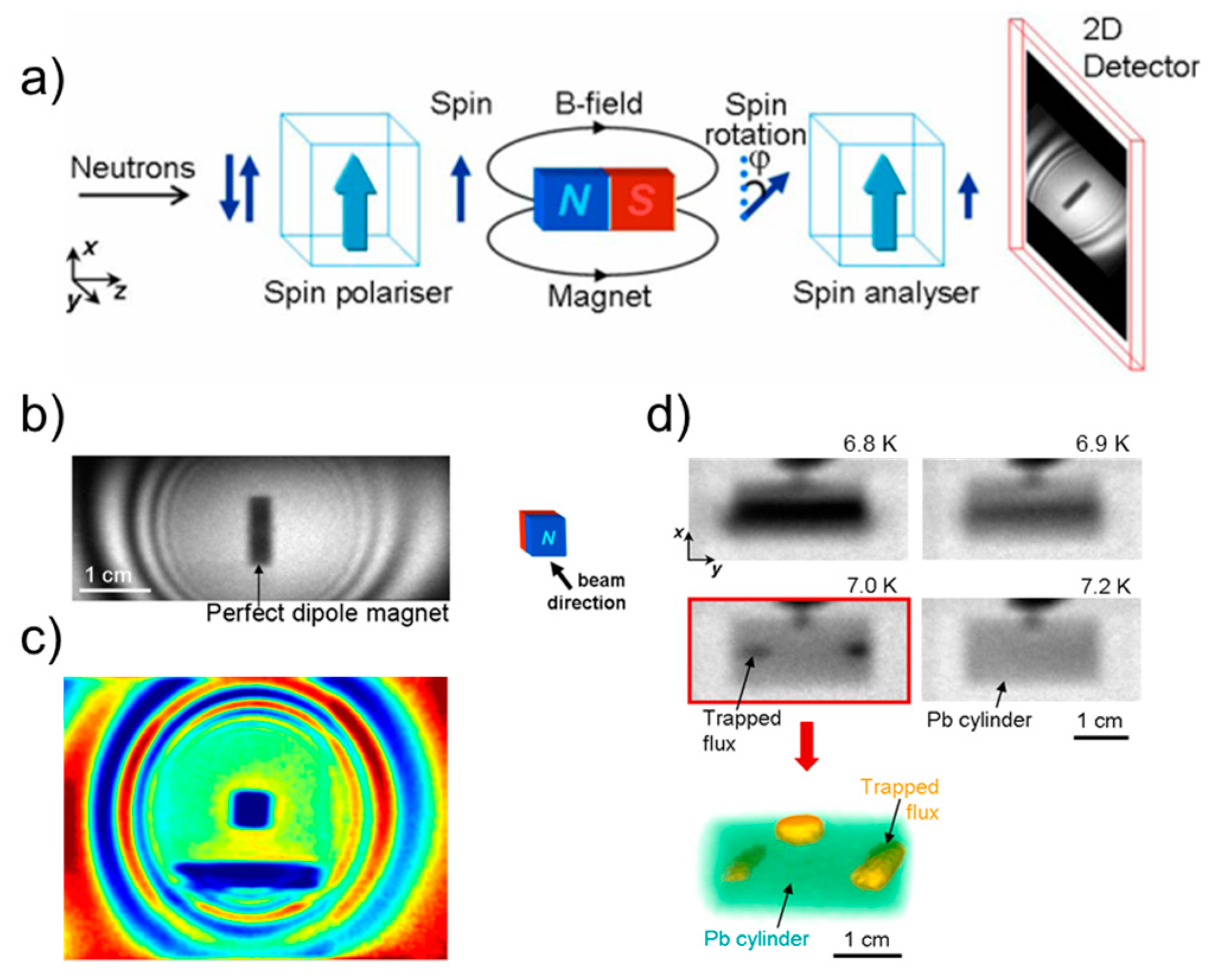
2. Experimental Techniques
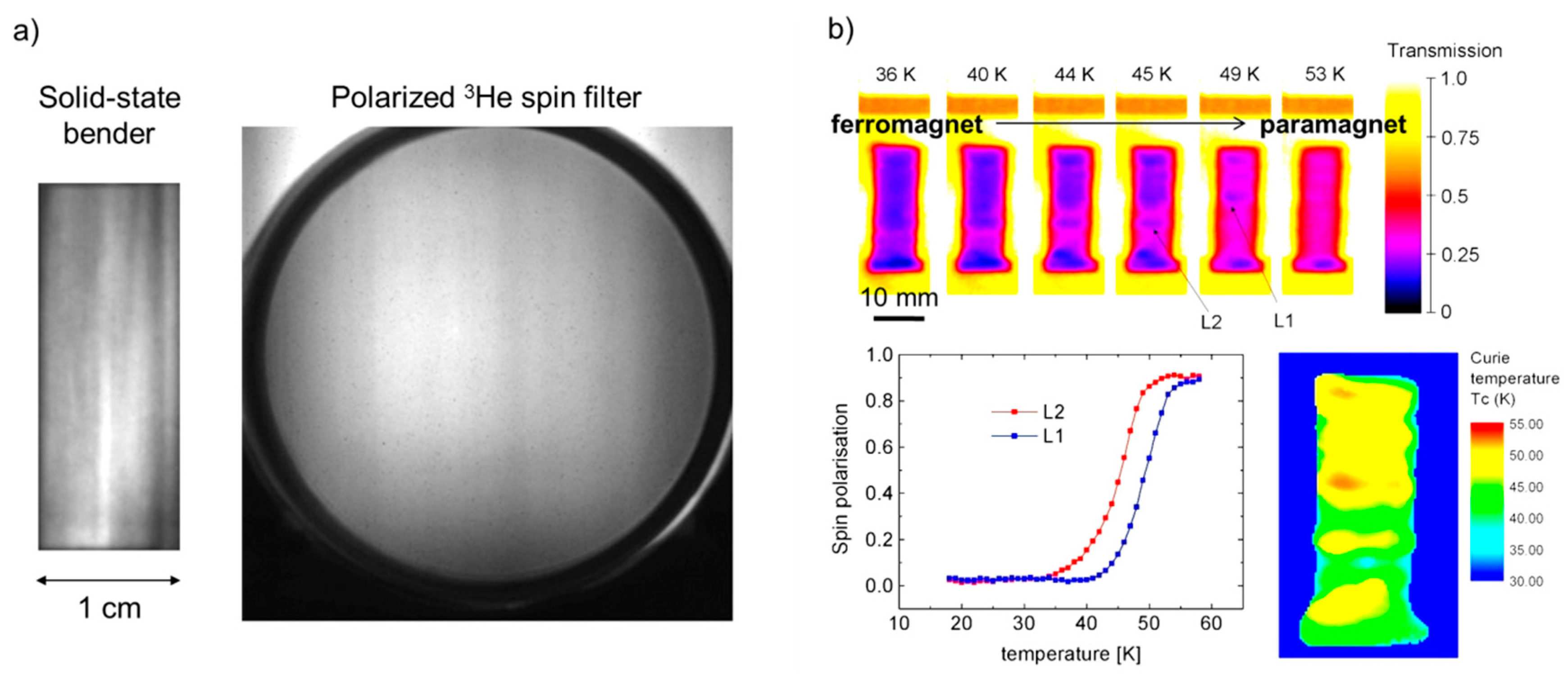
2.1. Solid-State Benders
2.2. Polarized 3He Spin Filters
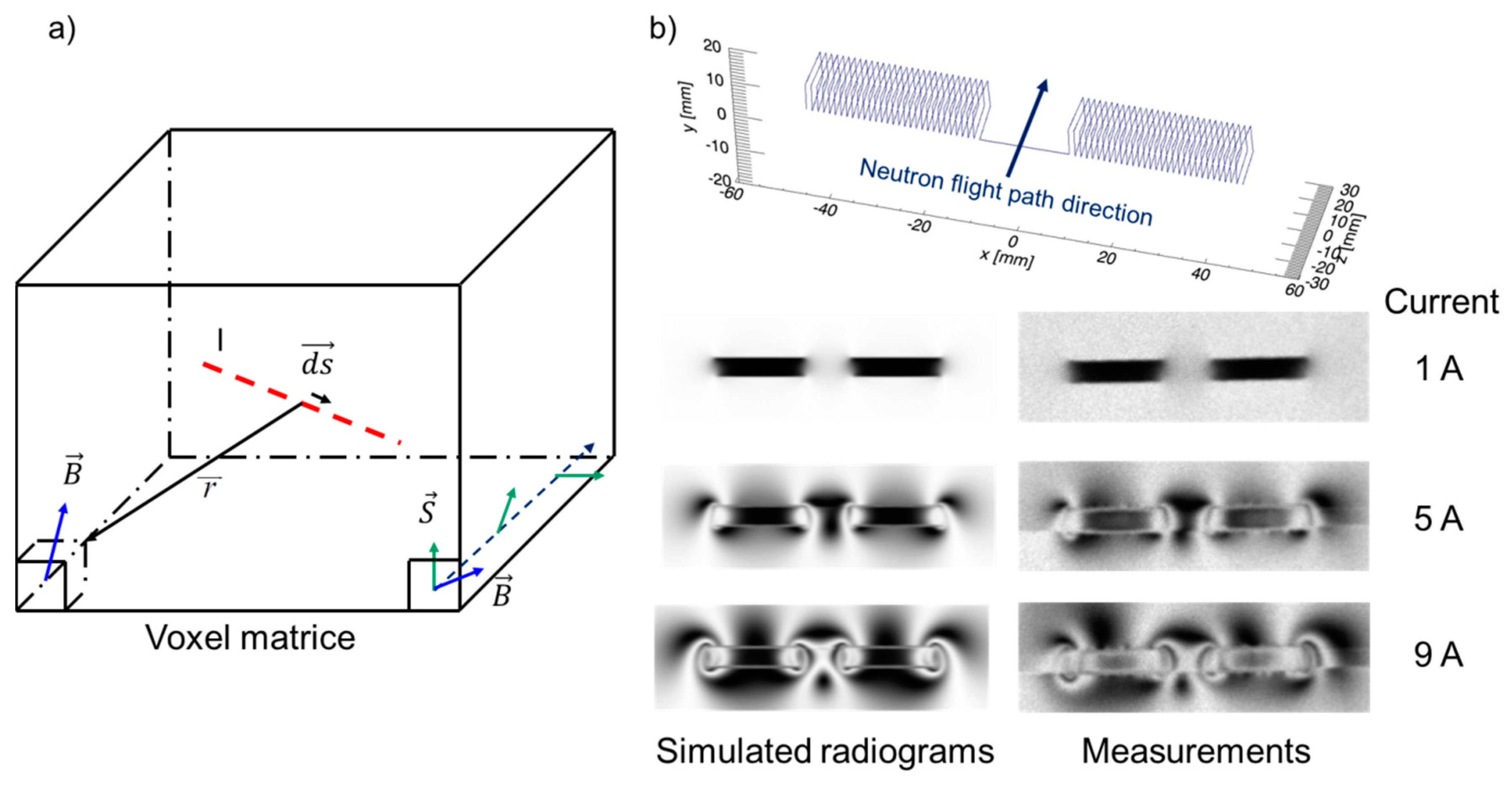
3. Simulation and Quantification of Magnetic Fields
4. Conclusions
Conflicts of Interest
References
- De Graef, M.; Zhu, Y. Preface. In Experimental Methods in the Physical Sciences; Marc De, G., Yimei, Z., Eds.; Academic Press: New York, NY, USA, 2001; pp. xv–xvi. [Google Scholar]
- Kardjilov, N.; Manke, I.; Strobl, M.; Hilger, A.; Treimer, W.; Meissner, M.; Krist, T.; Banhart, J. Three-dimensional imaging of magnetic fields with polarized neutrons. Nat. Phys. 2008, 4, 399–403. [Google Scholar] [CrossRef]
- Dawson, M.; Manke, I.; Kardjilov, N.; Hilger, A.; Strobl, M.; Banhart, J. Imaging with polarized neutrons. New J. Phys. 2009, 11, 043013. [Google Scholar] [CrossRef]
- Kardjilov, N.; Hilger, A.; Manke, I.; Strobl, M.; Dawson, M.; Banhart, J. New trends in neutron imaging. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2009, 605, 13–15. [Google Scholar] [CrossRef]
- Kardjilov, N.; Manke, I.; Hilger, A.; Strobl, M.; Banhart, J. Neutron imaging in materials science. Mater. Today 2011, 14, 248. [Google Scholar] [CrossRef]
- Williams, W.G. Polarized Neutrons; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Strobl, M.; Kardjilov, N.; Hilger, A.; Jericha, E.; Badurek, G.; Manke, I. Imaging with polarized neutrons. Phys. B Condens. Matter 2009, 404, 2611–2614. [Google Scholar] [CrossRef]
- Strobl, M.; Pappas, C.; Hilger, A.; Wellert, S.; Kardjilov, N.; Seidel, S.O.; Manke, I. Polarized neutron imaging: A spin-echo approach. Phys. B Condens. Matter 2011, 406, 2415–2418. [Google Scholar] [CrossRef]
- Krist, T.H.; Mezei, F. Solid state neutron polarisers and collimators. Proc. SPIE 2001, 4509. [Google Scholar] [CrossRef]
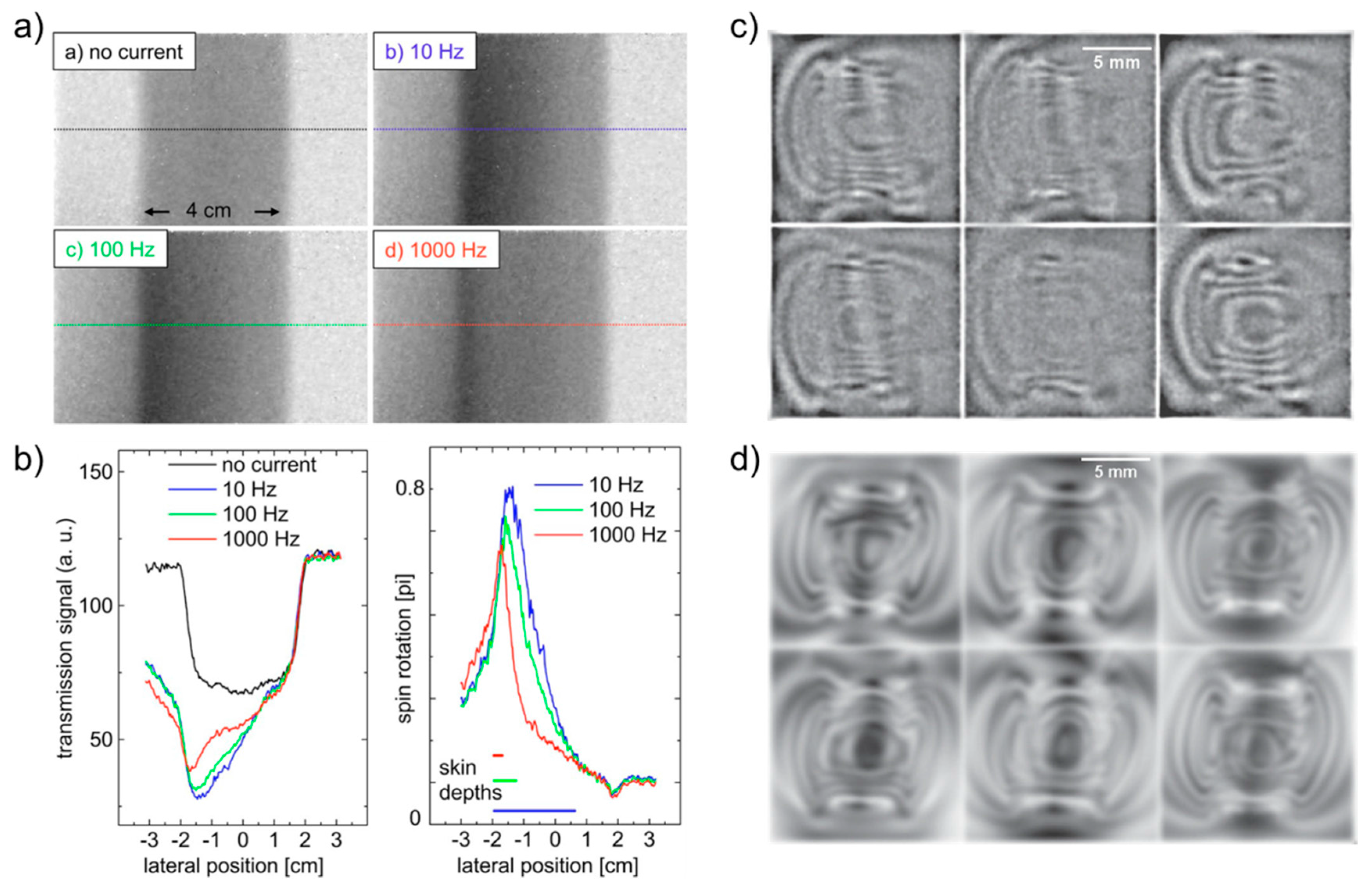
- Manke, I.; Kardjilov, N.; Strobl, M.; Hilger, A.; Banhart, J. Investigation of the skin effect in the bulk of electrical conductors with spin-polarized neutron radiography. J. Appl. Phys. 2008, 104, 076109. [Google Scholar] [CrossRef]
- Tremsin, A.S.; Kardjilov, N.; Strobl, M.; Manke, I.; Dawson, M.; McPhate, J.B.; Vallerga, J.V.; Siegmund, O.H.W.; Feller, W.B. Imaging of dynamic magnetic fields with spin-polarized neutron beams. New J. Phys. 2015, 17, 043047. [Google Scholar] [CrossRef]
- Dawson, M.; Kardjilov, N.; Manke, I.; Hilger, A.; Jullien, D.; Bordenave, F.; Strobl, M.; Jericha, E.; Badurek, G.; Banhart, J. Polarized neutron imaging using helium-3 cells and a polychromatic beam. Nuclear Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2011, 651, 140–144. [Google Scholar] [CrossRef]
- Michael, S.; Andreas, N.; Sergey, M.; Martin, M.; Elbio, C.; Burkhard, S.; Christian, P.; Peter, B. Towards a tomographic reconstruction of neutron depolarization data. J. Phys. Conf. Ser. 2010, 211, 012025. [Google Scholar]
- Dhiman, I.; Ziesche, R.; Wang, T.; Bilheux, H.; Santodonato, L.; Tong, X.; Jiang, C.Y.; Manke, I.; Treimer, W.; Chatterji, T.; et al. Setup for polarized neutron imaging using in situ 3He cells at the Oak Ridge National Laboratory High Flux Isotope Reactor CG-1D beamline. Rev. Sci. Instrum. 2017, 88, 095103. [Google Scholar] [CrossRef] [PubMed]
- Sales, M.; Strobl, M.; Shinohara, T.; Tremsin, A.; Kuhn, L.T.; Lionheart, W.R.B.; Desai, N.M.; Dahl, A.B.; Schmidt, S. Three Dimensional Polarimetric Neutron Tomography of Magnetic Fields. arXiv, 2017; arXiv:1704.04887. [Google Scholar]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kardjilov, N.; Hilger, A.; Manke, I.; Strobl, M.; Banhart, J. Imaging with Polarized Neutrons. J. Imaging 2018, 4, 23. https://doi.org/10.3390/jimaging4010023
Kardjilov N, Hilger A, Manke I, Strobl M, Banhart J. Imaging with Polarized Neutrons. Journal of Imaging. 2018; 4(1):23. https://doi.org/10.3390/jimaging4010023
Chicago/Turabian StyleKardjilov, Nikolay, André Hilger, Ingo Manke, Markus Strobl, and John Banhart. 2018. "Imaging with Polarized Neutrons" Journal of Imaging 4, no. 1: 23. https://doi.org/10.3390/jimaging4010023





