Development of an Electro-Thermal Model for Electric Vehicles Using a Design of Experiments Approach
Abstract
:1. Introduction
2. Experimental Procedure
2.1. Experimental Set-Up
2.2. Cell Characterization Experiments
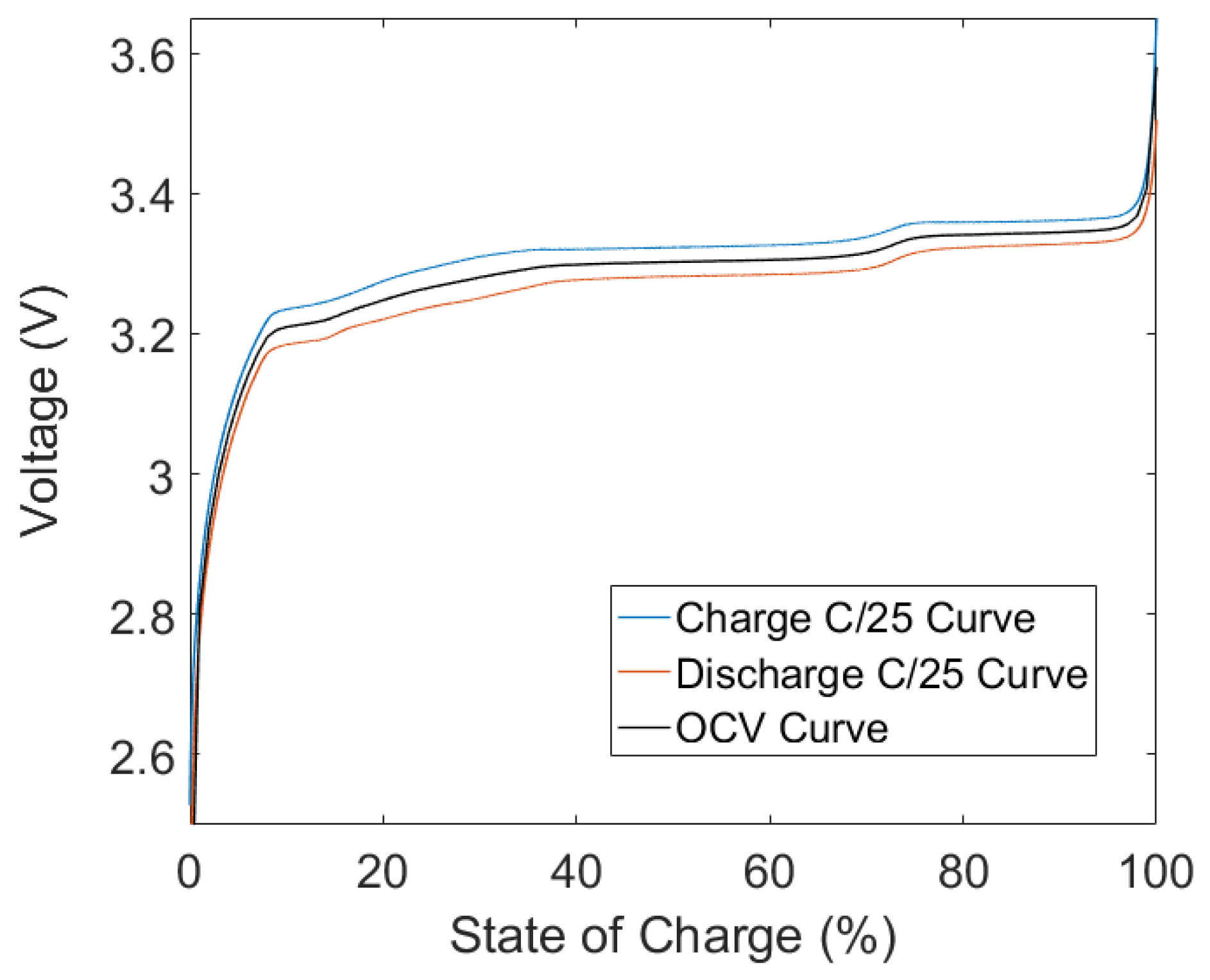
2.2.1. Open Circuit Voltage
- Charge the battery to full using a constant current of 1C and maintain the battery at 3.65 V until the current drops to below C/25. This is referred to as constant current constant voltage (CCCV) protocol.
- Allow the battery to rest for an hour.
- Discharge the battery at a constant current of C/25 until the lower limit of 2 V is reached.
- Allow the battery to rest for another hour.
- Charge the battery to full, once again using a constant current of C/25.
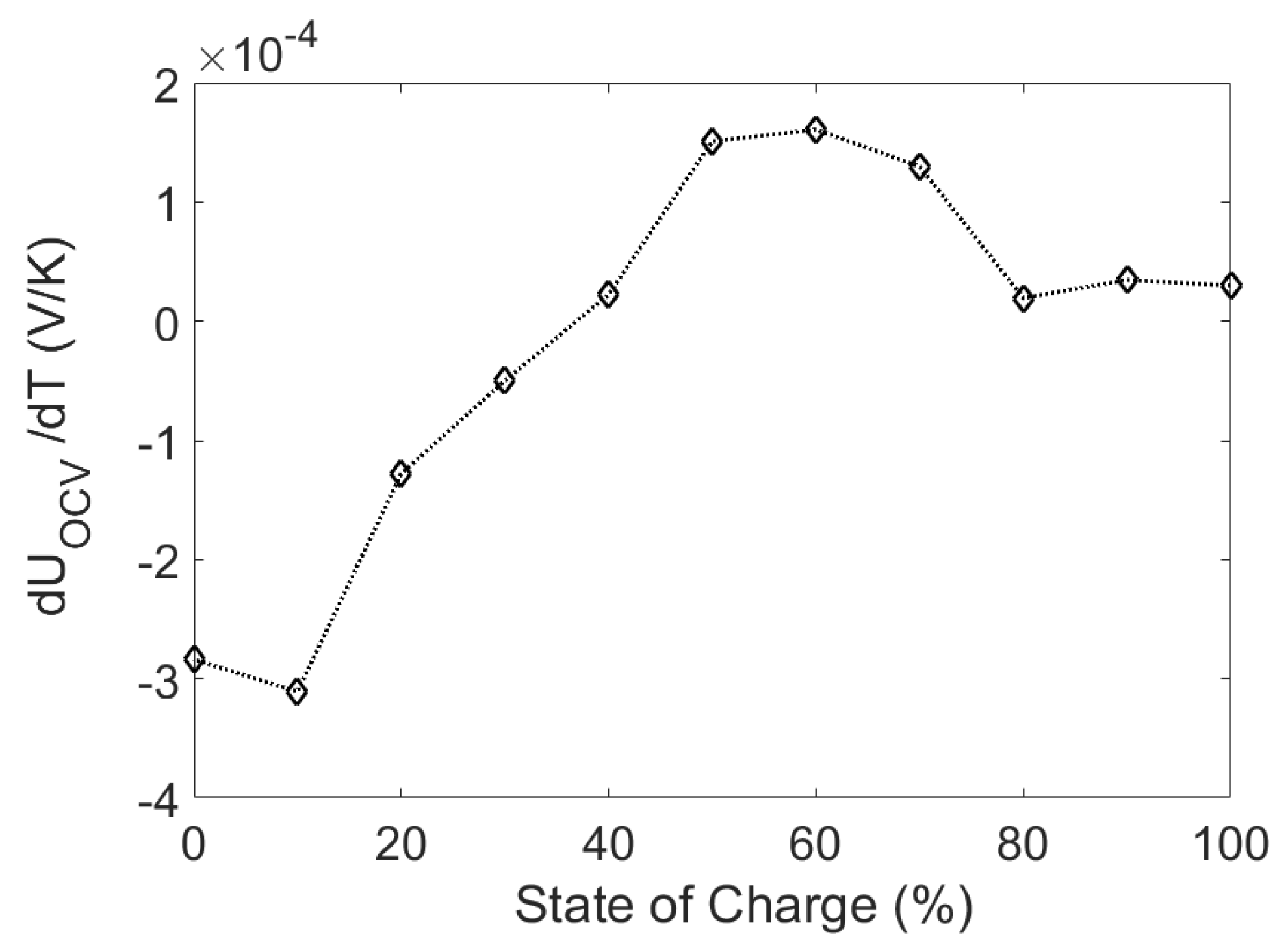
2.2.2. Entropic Heat Generation
- CCCV protocol was used to charge the cell to full.
- For the cell to reach its equilibrium voltage, the battery was rested for a total of 12 h at a constant temperature of 25 °C.
- The battery was then subjected to the temperature profile shown in Figure 3. The cell was assumed to have reached its equilibrium temperature after 3 h of rest.
- The battery was discharged to the next SOC point using a constant current discharge at 1C for 6 min. The cell was assumed to have reached its equilibrium voltage after 12 h of rest. The procedure was repeated until the cell was fully discharged.
2.2.3. Hybrid Pulse Power Characterization Test
- At a specific SOC value, discharge the battery at a constant current of 1C for 10 s.
- Allow the battery to rest for 40 s.
- Charge the battery at ¾C for 10 more seconds.
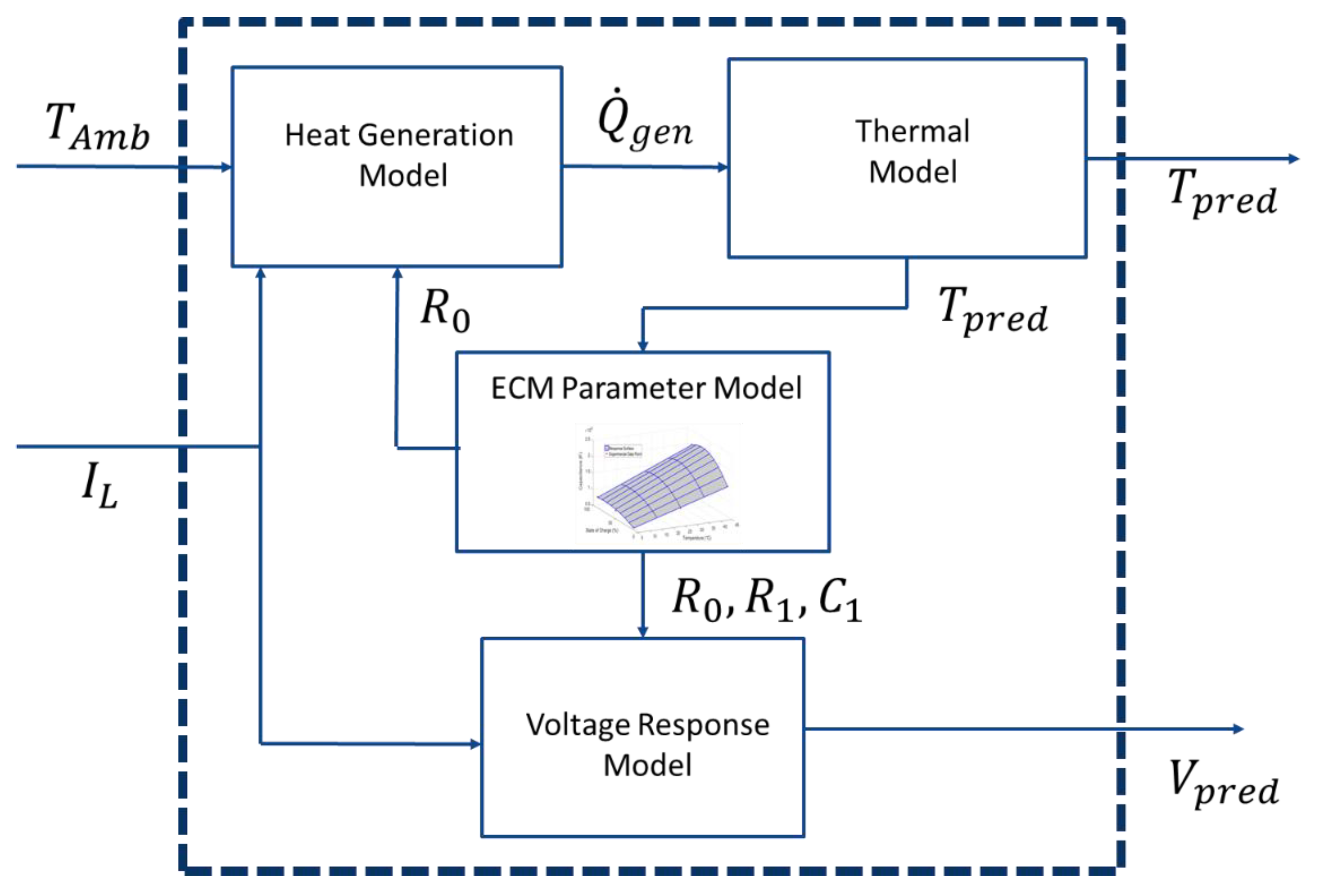
3. Algorithm Development
3.1. Voltage Response Sub-Model
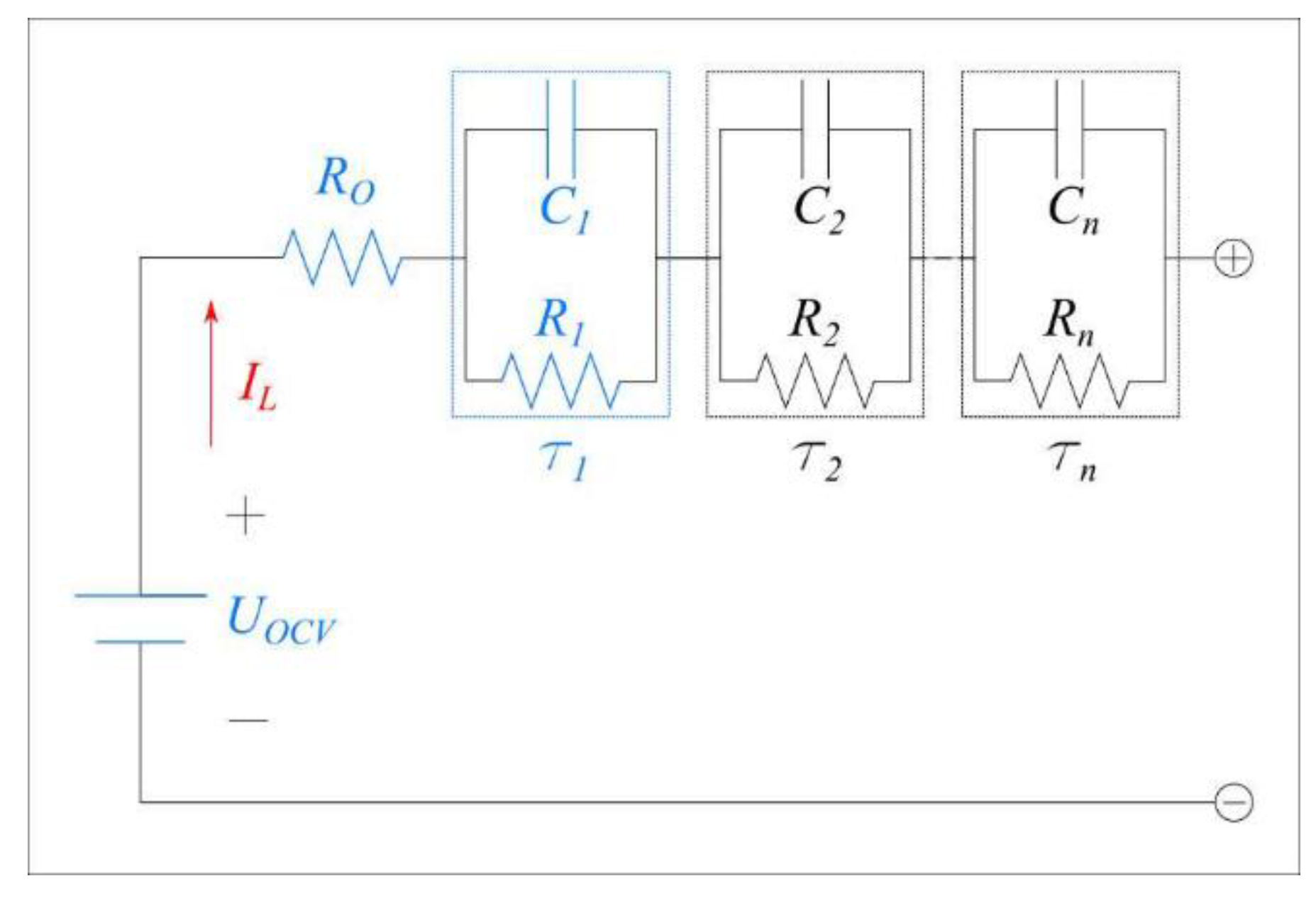
3.2. ECM Parameter Sub-Model
3.3. Thermal Response Sub-Model
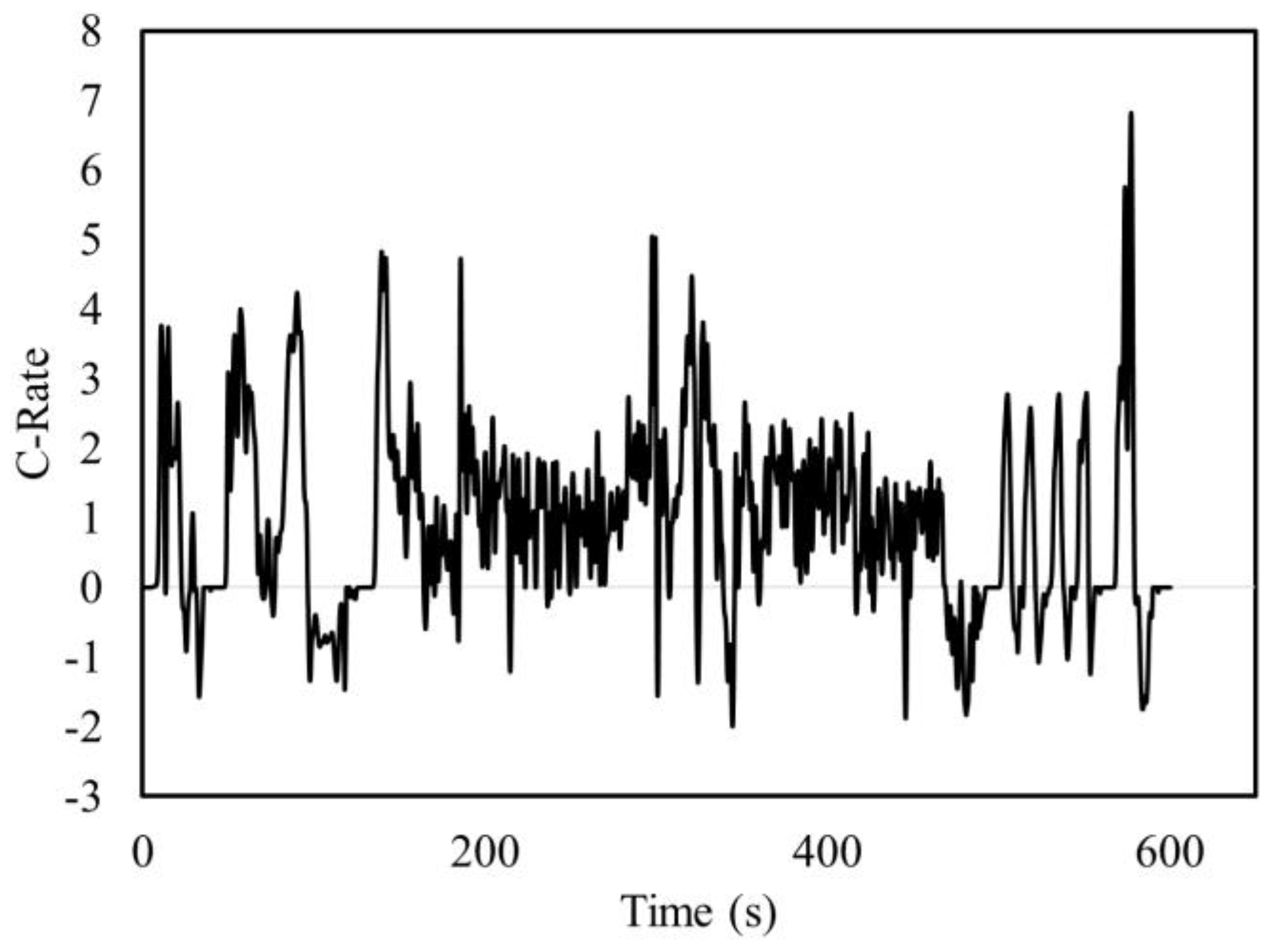
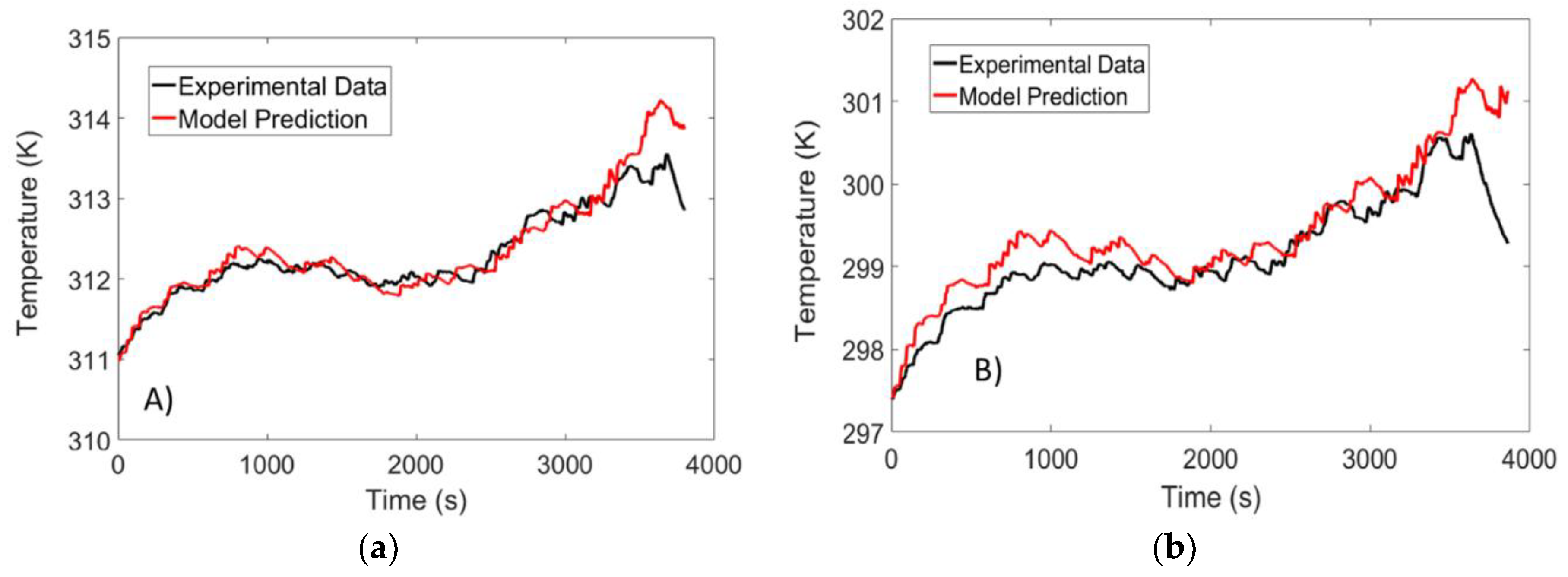
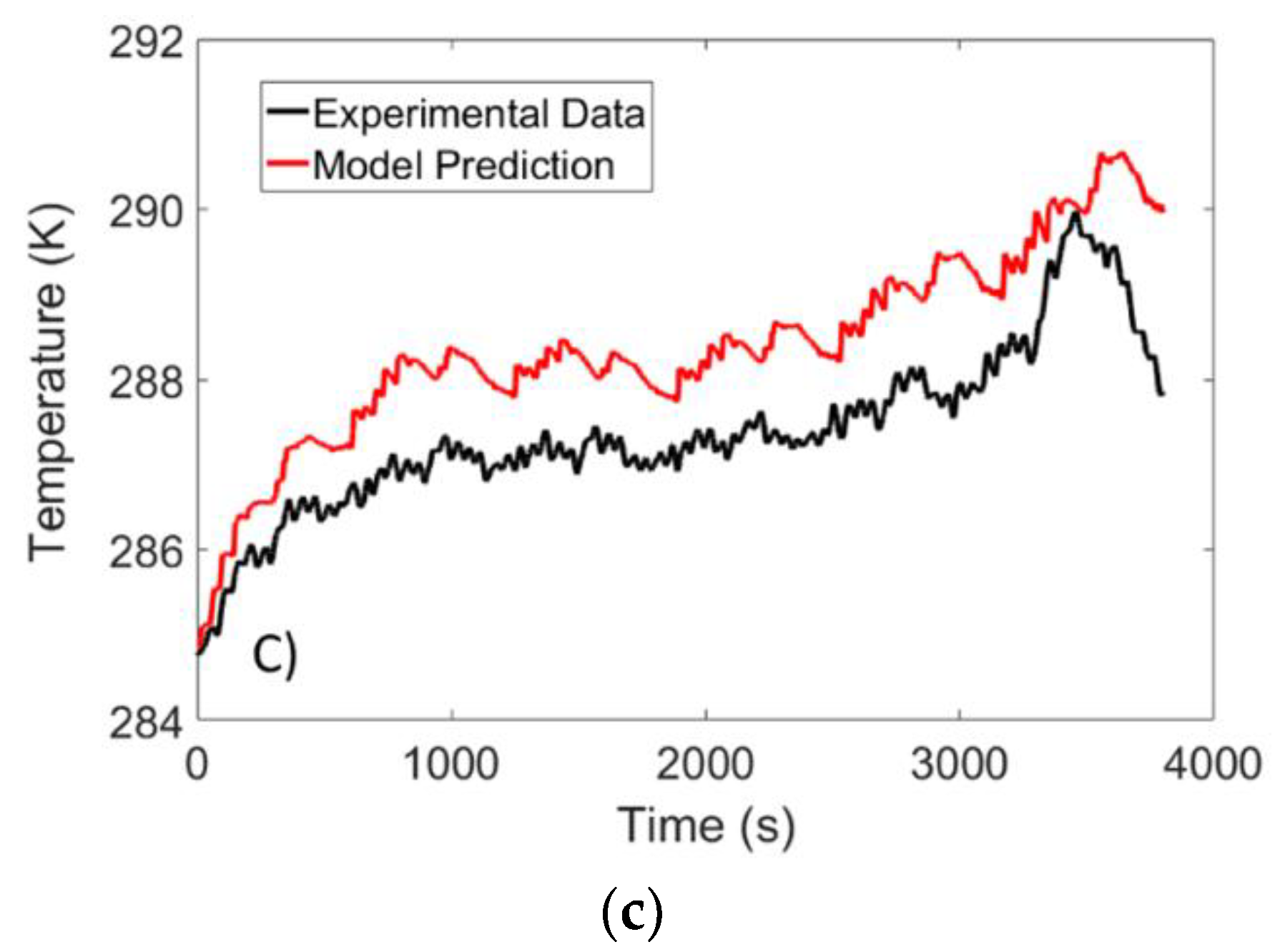
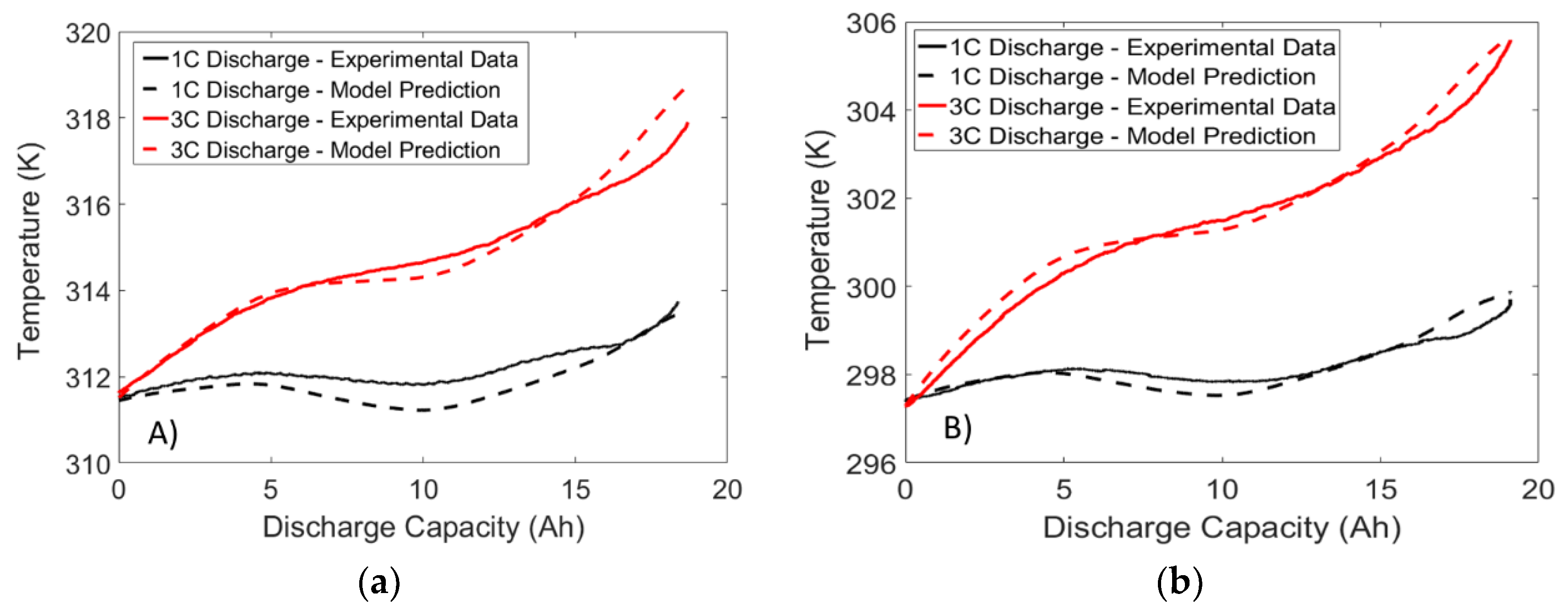
4. Results and Discussion
4.1. Cell Characterization Results
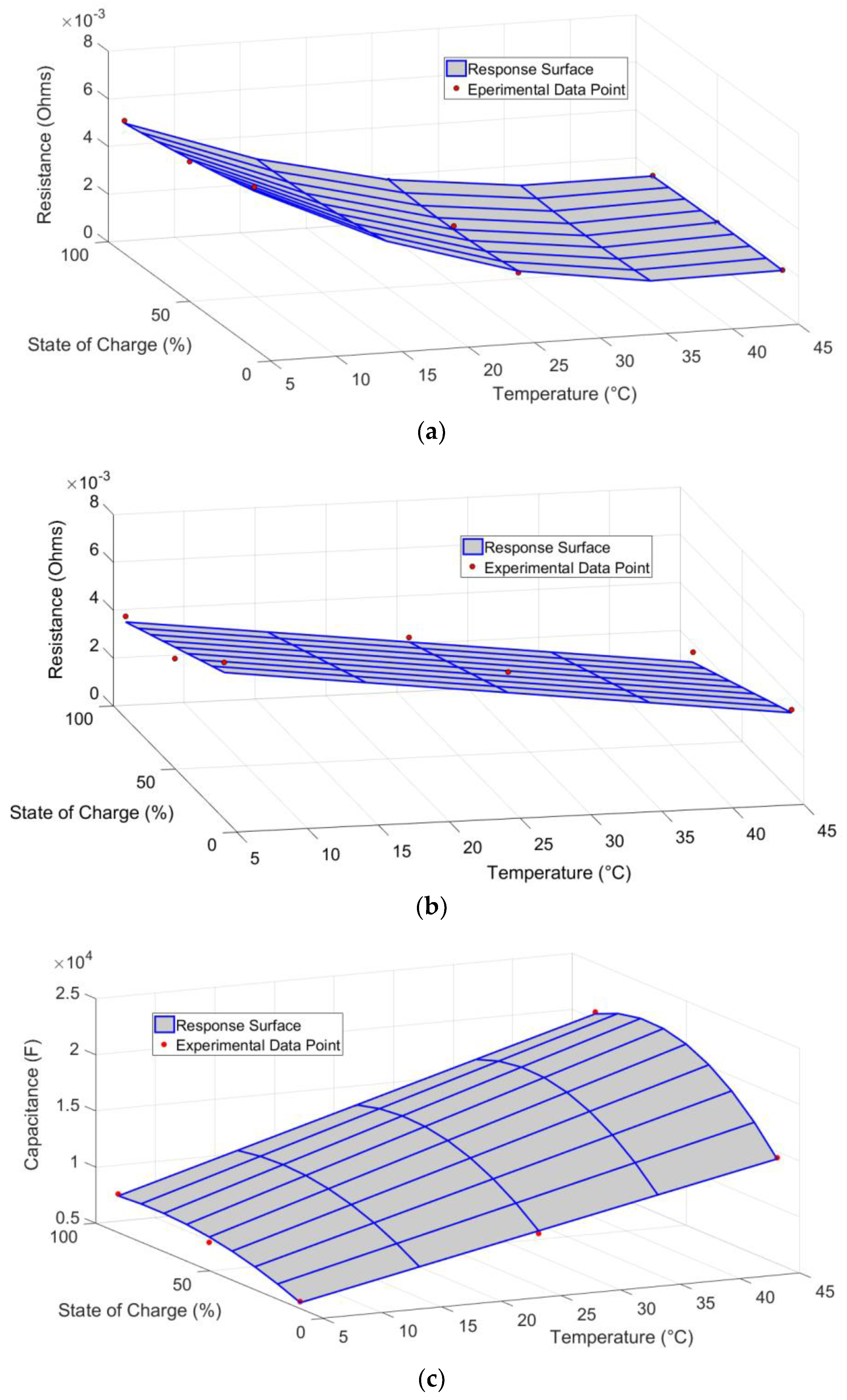
4.2. ECM Parameter Results
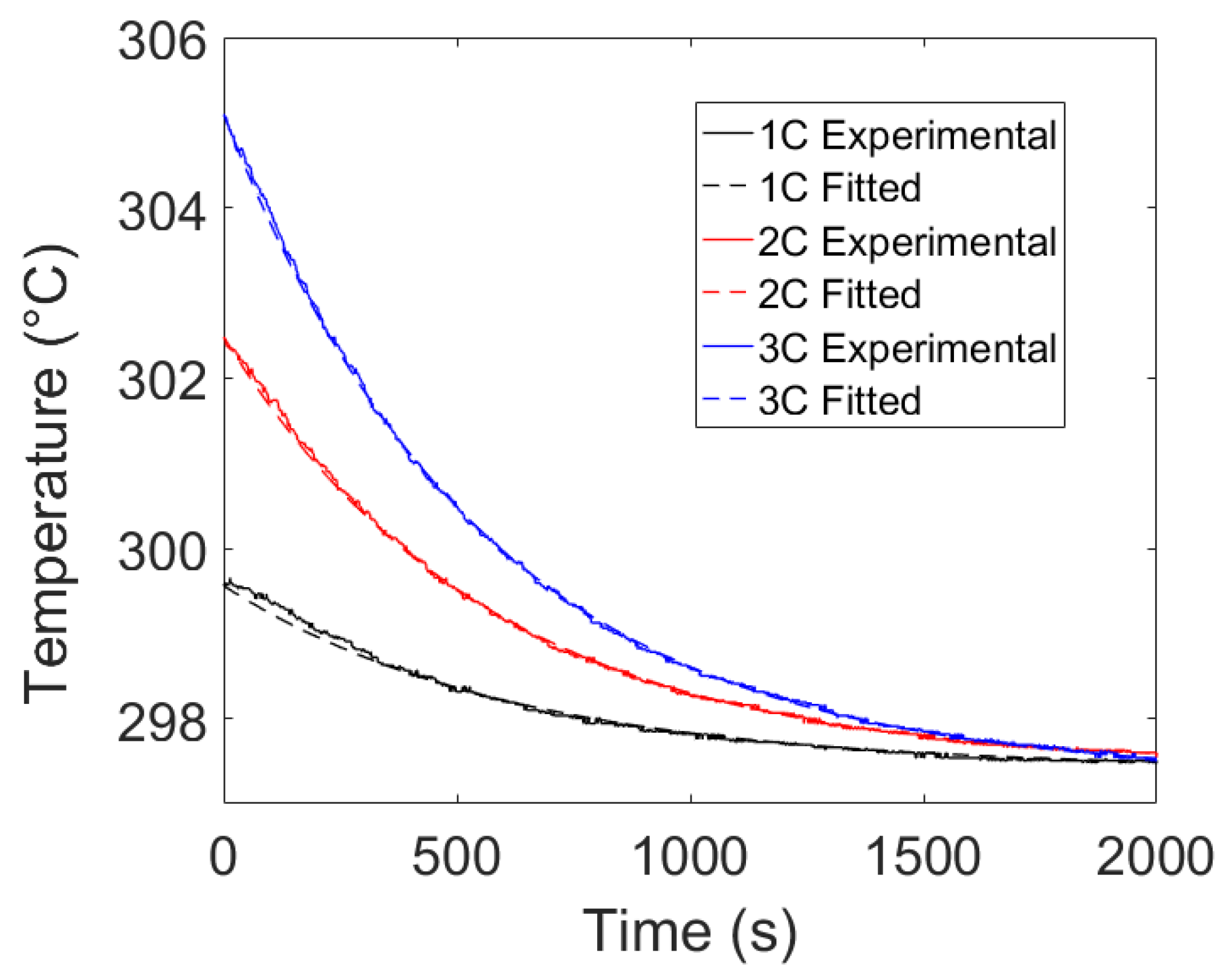
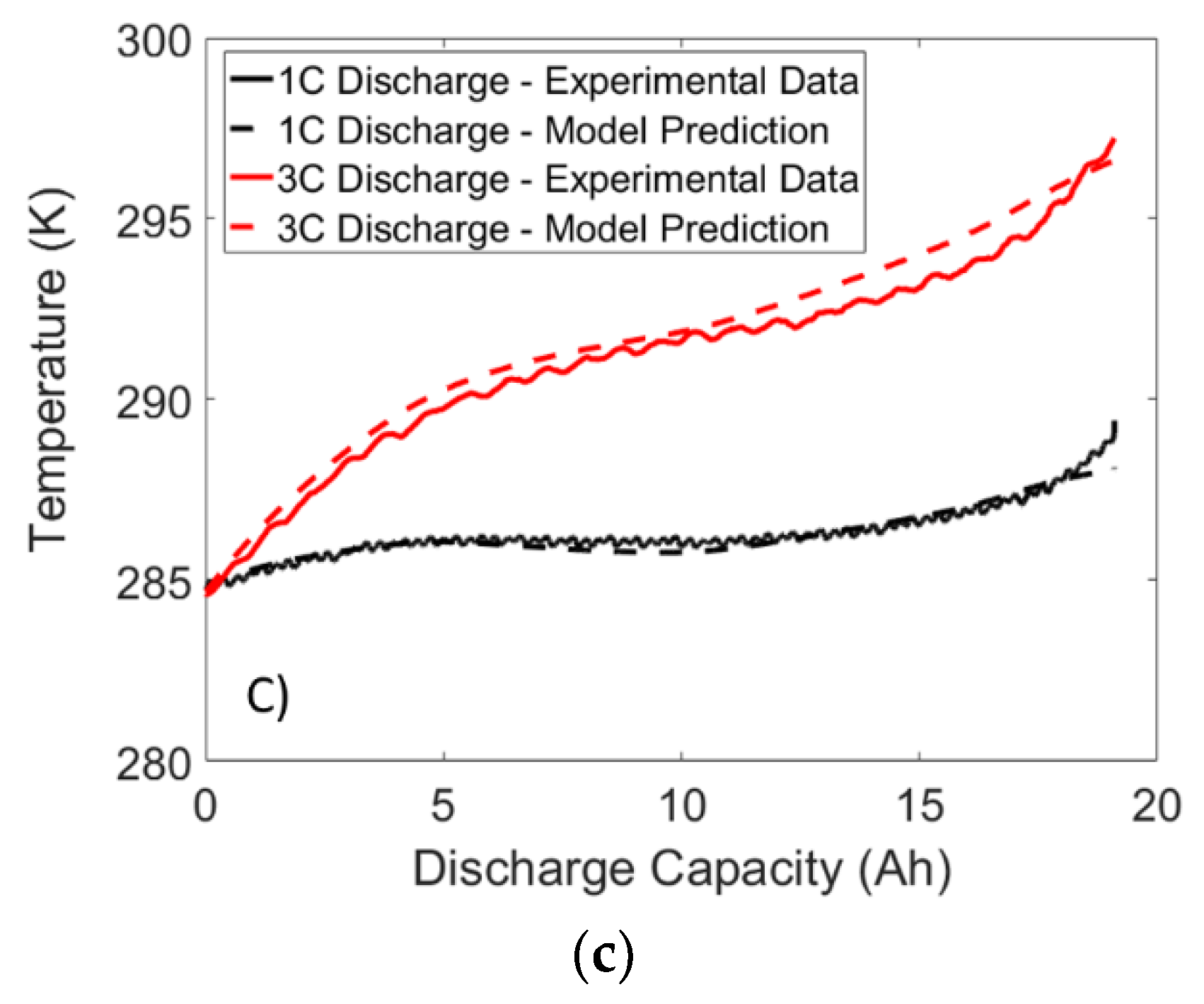
4.3. Temperature Validation Results
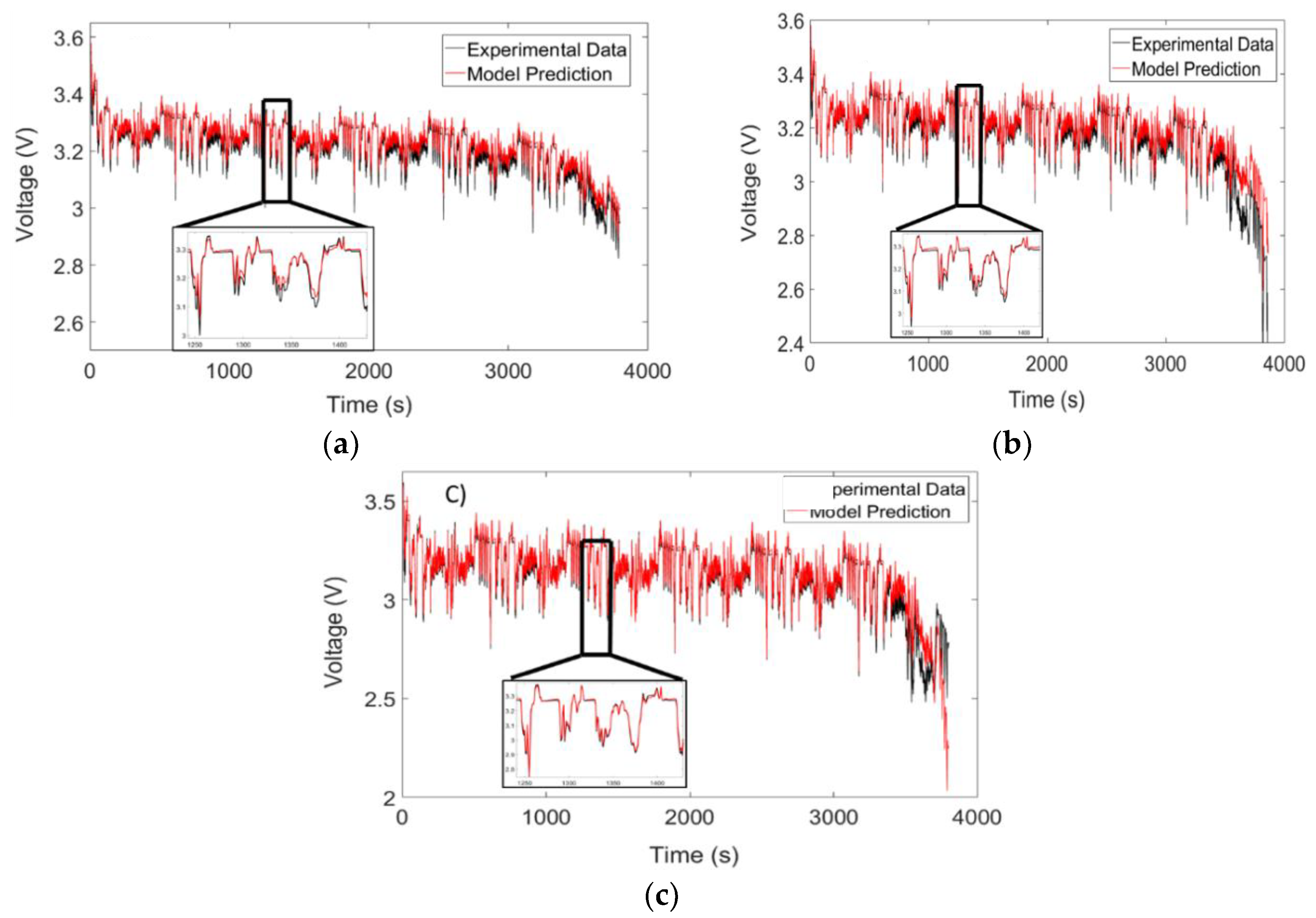
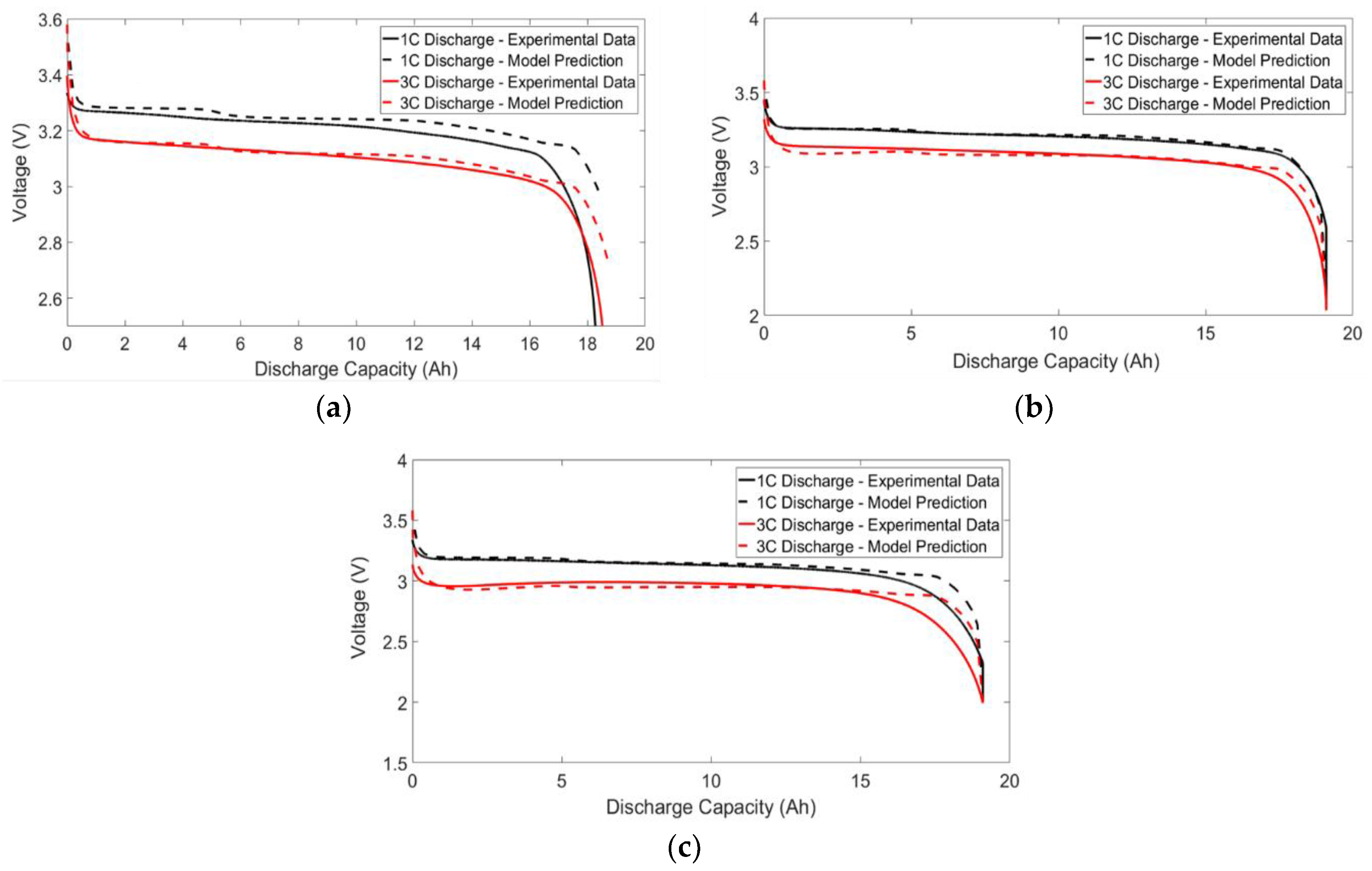
4.4. Voltage Validation Results
4.5. Comparison to Existing Approaches
5. Conclusions
- The model developed in this paper can accurately predict the temperature and voltage profiles of an LFP battery.
- All three ECM parameters were highly dependent on temperature and SOC, although only a linear dependence was observed for the Thevenin resistance.
- Replication runs are essential for accurately quantifying measurement noise and identifying which parameters in the model are significant. Conducting a statistical analysis is important as it allows one to draw conclusions on which factors affect the ECM parameters. This knowledge can be useful when developing robust state estimators that require determining the ECM parameters in real time.
- Using a DOE approach, the same degree of accuracy as existing techniques can be achieved while reducing the characterization time from 100 h to just 28 h. This time reduction is even more substantial if an additional SOH variable is added. Therefore, the DOE approach proposed in this paper provides a framework that future researchers can use to develop a comprehensive battery model that includes battery degradation.
Author Contributions
Funding
Conflicts of Interest
References
- Tarascon, J.; Armand, M. Issues and challenges facing rechargeable lithium batteries. Nature 2001, 414, 359–367. [Google Scholar] [CrossRef] [PubMed]
- Huat, L.; Ye, Y.; Tay, A.A.O. Integration issues of lithium-ion battery into electric vehicles battery pack. J. Clean. Prod. 2016, 113, 1032–1045. [Google Scholar]
- Manzetti, S.; Mariasiu, F. Electric vehicle battery technologies: From present state to future systems. Renew. Sustain. Energy Rev. 2015, 51, 1004–1012. [Google Scholar] [CrossRef]
- Santhanagopalan, S.; Guo, Q.; Ramadass, P.; White, R.E. Review of models for predicting the cycling performance of lithium ion batteries. J. Power Sources 2006, 156, 620–628. [Google Scholar] [CrossRef]
- Farkhondeh, M.; Delacourt, C. Mathematical Modeling of Commercial LiFePO4 Electrodes Based on Variable Solid-State Diffusivity. J. Electrochem. Soc. 2012, 159, A177–A192. [Google Scholar] [CrossRef]
- Mastali, M.; Farhad, S.; Farkhondeh, M.; Fraser, R.A.; Fowler, M. Simplified electrochemical multi-particle model for LiFePO4cathodes in lithium-ion batteries. J. Power Sources 2015, 275, 633–643. [Google Scholar] [CrossRef]
- Mastali, M.; Kohneh, M.; Samadani, E.; Fraser, R.; Fowler, M. Three-Dimensional Electrochemical Analysis of a Graphite/LiFePO4 Li-Ion Cell to Improve Its Durability; SAE Technical Paper; SAE: Detroit, MI, USA, 2015. [Google Scholar]
- Mastali, M.; Samadani, E.; Farhad, S.; Fraser, R.; Fowler, M. Three-dimensional Multi-Particle Electrochemical Model of LiFePO4 Cells based on a Resistor Network Methodology. Electrochim. Acta 2016, 190, 574–587. [Google Scholar] [CrossRef]
- Mastali, M.; Farkhondeh, M.; Farhad, S.; Fraser, R.A.; Fowler, M. Electrochemical Modeling of Commercial LiFePO4 and Graphite Electrodes : Kinetic and Transport Properties and Their Temperature Dependence. J. Electrochem. Soc. 2016, 163, A2803–A2816. [Google Scholar] [CrossRef]
- Panchal, S.; Mathew, M.; Fraser, R.; Fowler, M. Electrochemical thermal modeling and experimental measurements of 18650 cylindrical lithium-ion battery during discharge cycle for an EV. Appl. Therm. Eng. 2018, 135, 123–132. [Google Scholar] [CrossRef]
- Seaman, A.; Dao, T.-S.; McPhee, J. A survey of mathematics-based equivalent-circuit and electrochemical battery models for hybrid and electric vehicle simulation. J. Power Sources 2014, 256, 410–423. [Google Scholar] [CrossRef] [Green Version]
- Samadani, E.; Farhad, S.; Scott, W.; Mastali, M.; Gimenez, L.E.; Fowler, M.; Fraser, R.A. Empirical Modeling of Lithium-ion Batteries Based on Electrochemical Impedance Spectroscopy Tests. Electrochim. Acta 2015, 160, 169–177. [Google Scholar] [CrossRef]
- Mathew, M.; Kong, Q.H.; McGrory, J.; Fowler, M. Simulation of lithium ion battery replacement in a battery pack for application in electric vehicles. J. Power Sources 2017, 349, 94–104. [Google Scholar] [CrossRef]
- Murashko, K.; Pyrhonen, J.; Laurila, L. Three-dimensional thermal model of a lithium ion battery for hybrid mobile working machines: Determination of the model parameters in a pouch cell. IEEE Trans. Energy Convers. 2013, 28, 335–343. [Google Scholar] [CrossRef]
- Samadani, E.; Mastali, M.; Farhad, S.; Fraser, R.A.; Fowler, M. Li-ion battery performance and degradation in electric vehicles under different usage scenarios. Int. J. Energy Res. 2015, 40, 379–392. [Google Scholar] [CrossRef]
- Hu, Y.; Yurkovich, S.; Guezennec, Y.; Yurkovich, B.J. Electro-thermal battery model identification for automotive applications. J. Power Sources 2010, 196, 449–457. [Google Scholar] [CrossRef]
- Lin, X.; Perez, H.E.; Mohan, S.; Siegel, J.B.; Stefanopoulou, A.G.; Ding, Y.; Castanier, M.P. A lumped-parameter electro-thermal model for cylindrical batteries. J. Power Sources 2014, 257, 1–11. [Google Scholar] [CrossRef]
- Samadani, E.; Gimenez, L.; Scott, W.; Farhad, S.; Fowler, M.; Fraser, R. Thermal Behavior of Two Commercial Li-Ion Batteries for Plug-in Hybrid Electric Vehicles; SAE Technical Paper; SAE: Detroit, MI, USA, 2014. [Google Scholar]
- Damay, N.; Forgez, C.; Bichat, M.P.; Friedrich, G. Thermal modeling of large prismatic LiFePO4/graphite battery. Coupled thermal and heat generation models for characterization and simulation. J. Power Sources 2015, 283, 37–45. [Google Scholar] [CrossRef]
- Jaguemont, J.; Boulon, L.; Dube, Y. Characterization and Modeling of a Hybrid-Electric-Vehicle Lithium-Ion Battery Pack at Low Temperatures. IEEE Trans. Veh. Technol. 2016, 65, 1–14. [Google Scholar] [CrossRef]
- Mastali, M.; Foreman, E.; Modjtahedi, A.; Samadani, E.; Amirfazli, A.; Farhad, S.; Fraser, R.A.; Fowler, M. Electrochemical-thermal modeling and experimental validation of commercial graphite/LiFePO4 pouch lithium-ion batteries. Int. J. Therm. Sci. 2018, 129, 218–230. [Google Scholar] [CrossRef]
- Montgomery, D. Design and Analysis of Experiments, 8th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013. [Google Scholar]
- Khuri, A.; Mukhopadhyay, S. Response surface methodology. Comput. Stat. 2010, 2, 128–149. [Google Scholar] [CrossRef] [Green Version]
- Vera, L.; De Zan, M.M.; Cámara, M.S.; Goicoechea, C. Talanta Experimental design and multiple response optimization. Using the desirability function in analytical methods development. Talanta 2014, 124, 123–138. [Google Scholar] [CrossRef] [PubMed]
- Rao, L.; Newman, J. Heat-Generation Rate and General Energy Balance for Insertion Battery Systems. Electrochem. Soc. 1997, 144, 2697–2704. [Google Scholar] [CrossRef]
- Mastali, M. Electrochemical-Thermal Modeling of Lithium-ion Batteries. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, 2016. [Google Scholar]
- Bandhauer, T.M.; Garimella, S.; Fuller, T.F. A Critical Review of Thermal Issues in Lithium-Ion Batteries. J. Electrochem. Soc. 2011, 158, R1–R25. [Google Scholar] [CrossRef]
- Jalkanen, K.; Aho, T.; Vuorilehto, K. Entropy change effects on the thermal behavior of a LiFePO4/graphite lithium-ion cell at different states of charge. J. Power Sources 2013, 243, 354–360. [Google Scholar] [CrossRef]
- Farag, M.; Sweity, H.; Fleckenstein, M.; Habibi, S. Combined electrochemical, heat generation, and thermal model for large prismatic lithium-ion batteries in real-time applications. J. Power Sources 2017, 360, 618–633. [Google Scholar] [CrossRef]
- Sun, J.; Wei, G.; Pei, L.; Lu, R.; Song, K.; Wu, C.; Zhu, C. Online internal temperature estimation for lithium-ion batteries based on Kalman filter. Energies 2015, 8, 4400–4415. [Google Scholar] [CrossRef]

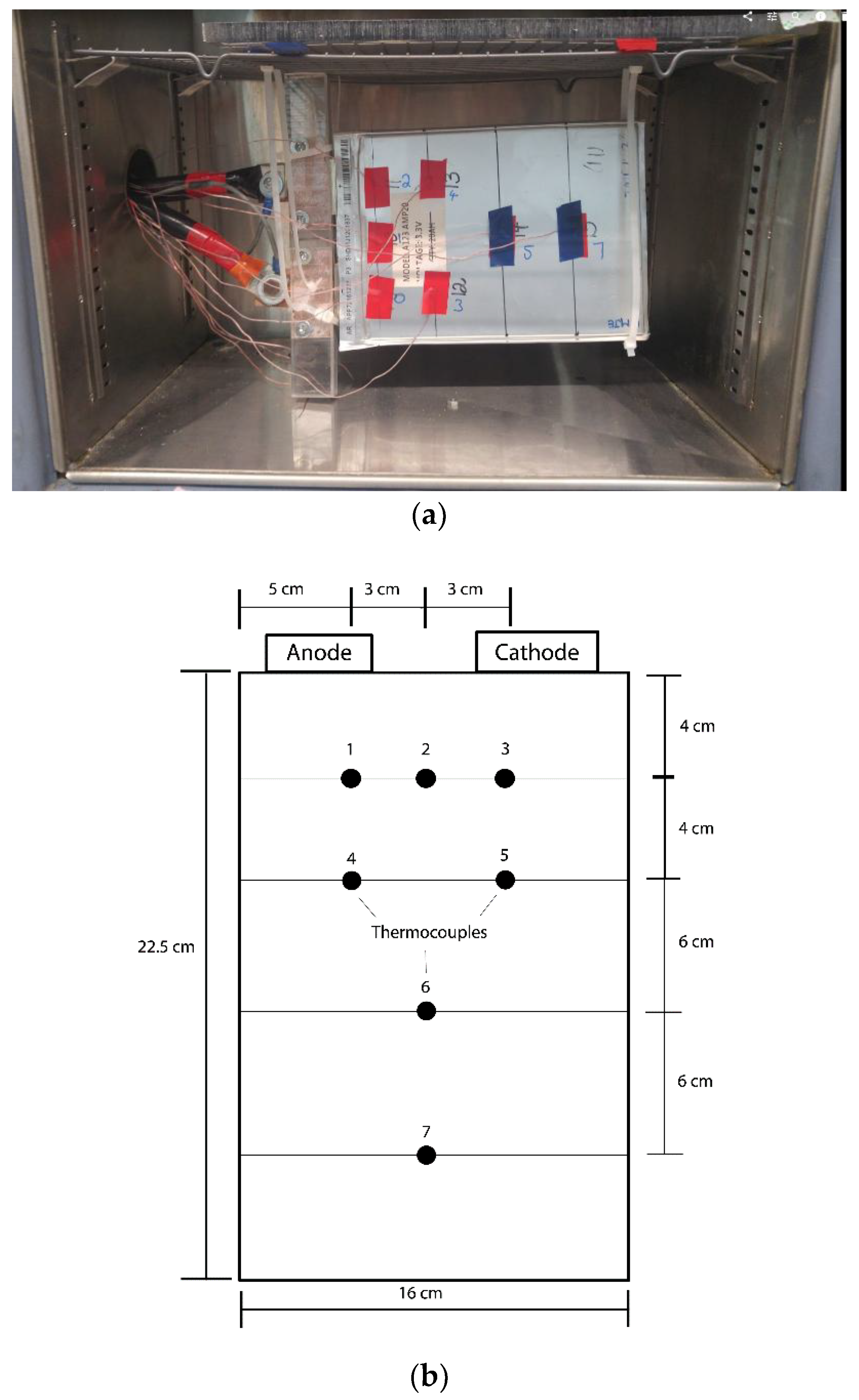

| Parameter | A123 Battery |
|---|---|
| Cathode Material | LiFePO4 |
| Anode Material | Graphite |
| Dimension (mm) | 7.25 × 160 × 227 |
| Mass (g) | 496 |
| Rated Capacity (Ahr) | 20 |
| Nominal Voltage (V) | 3.3 |
| Type | Temperature (°C) | SOC (%) |
|---|---|---|
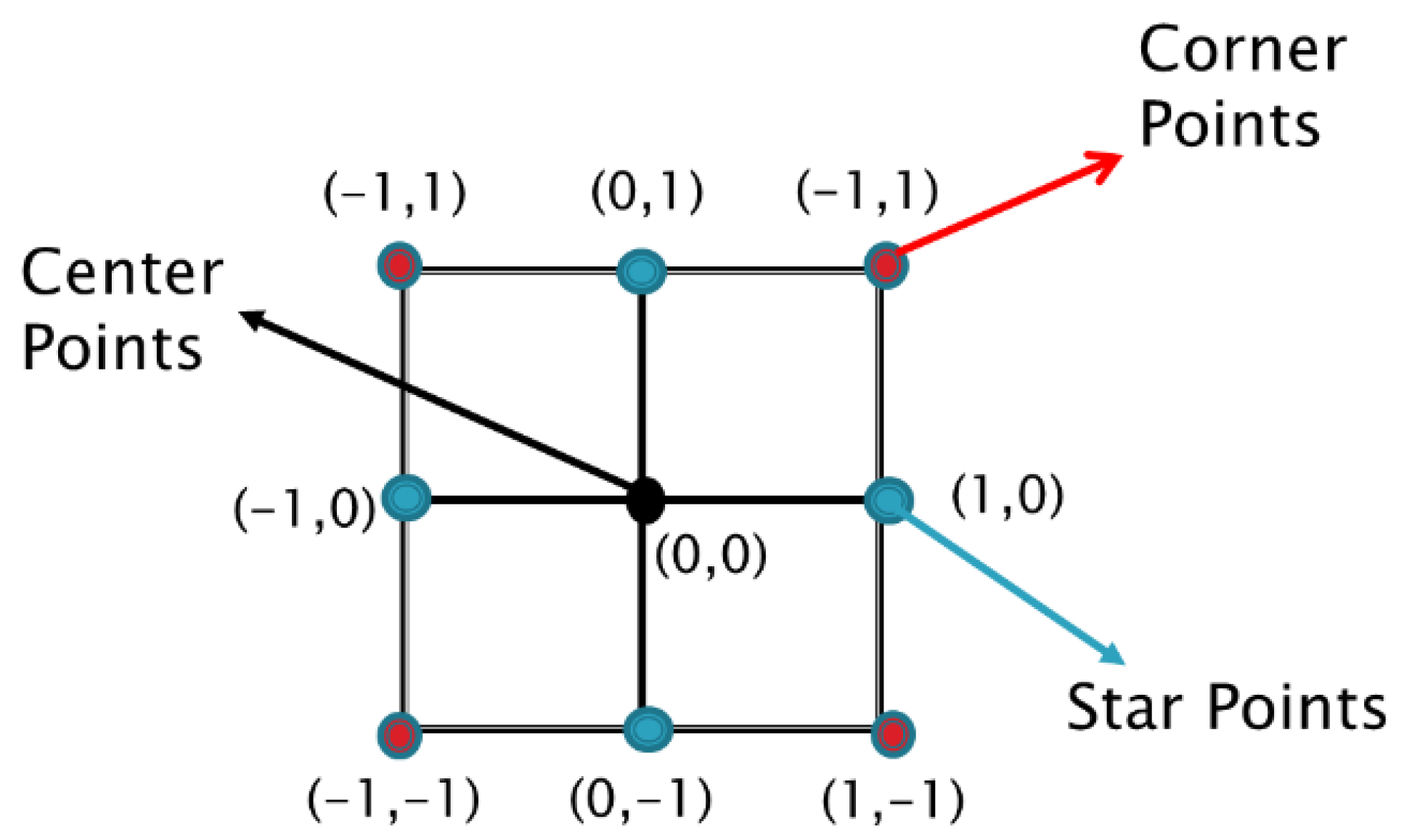
| Corner and Star Points | 5 | 10 |
| 5 | 50 | |
| 5 | 90 | |
| 25 | 10 | |
| 25 | 50 | |
| 25 | 90 | |
| 45 | 10 | |
| 45 | 50 | |
| 45 | 90 | |
| Replicate Run | 25 | 50 |
| 25 | 50 | |
| 25 | 50 | |
| 25 | 50 | |
| 25 | 50 |
| ECM Parameters | Measurement Error |
|---|---|
| Ohmic Resistance (Ohms) | 1.88 × 10−5 |
| Thevenin Resistance (Ohms) | 5.02 × 10−4 |
| Thevenin Capacitance (F) | 2.18 × 102 |
| Ohmic Resistance Response Surface | |||
| Type | Parameter Estimate | Standard Error | p-Value |
| Intercept | 2.39 × 10−3 | 1.88 × 10−5 | <0.0001 |
| Temp | −2.06 × 10−3 | 1.33 × 10−5 | <0.0001 |
| SOC | −7.14 × 10−5 | 1.33 × 10−5 | 0.0058 |
| Temp2 | 1.43 × 10−3 | 2.30 × 10−5 | <0.0001 |
| SOC2 | −1.93 × 10−5 | 2.30 × 10−5 | 0.448 |
| Temp × SOC | 2.93 × 10−4 | 9.38 × 10−6 | <0.0001 |
| Temp2 × SOC | −2.48 × 10−4 | 1.62 × 10−5 | 0.0001 |
| SOC2 × Temp | −1.58 × 10−4 | 1.62 × 10−5 | 0.0006 |
| SOC2 × Temp2 | 1.77 × 10−4 | 2.81 × 10−5 | 0.0032 |
| Thevenin Resistance Response Surface | |||
| Type | Parameter Estimate | Standard Error | p-Value |
| Intercept | 3.00 × 10−3 | 5.02 × 10−4 | 0.0039 |
| Temp | −1.35 × 10−3 | 3.55 × 10−4 | 0.0191 |
| SOC | −1.38 × 10−3 | 3.55 × 10−4 | 0.0175 |
| Temp2 | 2.63 × 10−4 | 6.14 × 10−4 | 0.4893 |
| SOC2 | 1.20 × 10−3 | 6.14 × 10−4 | 0.1222 |
| Temp × SOC | 1.18 × 10−4 | 2.51 × 10−4 | 0.6637 |
| Temp2 × SOC | 3.53 × 10−4 | 4.34 × 10−4 | 0.4620 |
| SOC2 × Temp | −9.91 × 10−5 | 4.34 × 10−4 | 0.8305 |
| SOC2 × Temp2 | −4.94 × 10−4 | 7.53 × 10−4 | 0.5475 |
| Thevenin Capacitance Response Surface | |||
| Type | Parameter Estimate | Standard Error | p-Value |
| Intercept | 1.41 × 104 | 2.18 × 102 | <0.0001 |
| Temp | 6.27 × 103 | 1.54 × 102 | <0.0001 |
| SOC | 2.16 × 103 | 1.54 × 102 | 0.0002 |
| Temp2 | −2.88 × 102 | 2.67 × 102 | 0.3409 |
| SOC2 | −2.22 × 103 | 2.67 × 102 | 0.0011 |
| Temp × SOC | 8.51 × 102 | 1.09 × 102 | 0.0015 |
| Temp2 × SOC | 7.99 × 10 | 1.89 × 102 | 0.6943 |
| SOC2 × Temp | −1.04 × 103 | 1.89 × 102 | 0.0052 |
| SOC2 × Temp2 | 7.35 × 102 | 3.27 × 102 | 0.0879 |
| Ohmic Resistance | Thevenin Resistance | Thevenin Capacitance | |||
|---|---|---|---|---|---|
| Intercept | 8.39 × 10−3 | Intercept | 6.76 × 10−3 | Intercept | 3.75× 103 |
| Temp | −3.35 × 10−4 | Temp | −7.07 × 10−5 | Temp | 1.71 × 102 |
| SOC | −1.93 × 10−5 | SOC | −2.63 × 10−5 | SOC | 7.60 × 10 |
| Temp2 | 4.16 × 10−6 | SOC2 | −4.74 × 10−1 | ||
| Temp × SOC | 2.24 × 10−9 | Temp × SOC | 5.25 × 100 | ||
| Temp2 × SOC | 1.04 × 10−8 | SOC2 × Temp | −4.19 × 10−2 | ||
| SOC2 × Temp | 1.02 × 10−8 | ||||
| SOC2 × Temp2 | −2.40 × 10−10 | ||||
| Temperature RMSE (K) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Type | 10 °C | 25 °C | 40 °C | ||||||
| LUT | Non-DOE | CCD | LUT | Non-DOE | CCD | LUT | Non-DOE | CCD | |
| 1C Discharge | 0.17 | 0.17 | 0.18 | 0.17 | 0.17 | 0.19 | 0.34 | 0.40 | 0.44 |
| 3C Discharge | 0.60 | 0.65 | 0.57 | 0.59 | 0.35 | 0.26 | 0.47 | 0.33 | 0.25 |
| us 06 | 0.95 | 1.07 | 1.07 | 0.37 | 0.32 | 0.25 | 0.31 | 0.18 | 0.13 |
| Average | 0.57 | 0.63 | 0.61 | 0.38 | 0.28 | 0.23 | 0.37 | 0.30 | 0.27 |
| Voltage RMSE (mV) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Type | 10 °C | 25 °C | 40 °C | ||||||
| LUT | Non-DOE | CCD | LUT | Non-DOE | CCD | LUT | Non-DOE | CCD | |
| 1C Discharge | 35.7 | 31.9 | 29.3 | 9.1 | 10.3 | 11.5 | 30.0 | 35.1 | 38.5 |
| 3C Discharge | 45.0 | 47.1 | 40.9 | 38.9 | 29.6 | 21.2 | 15.8 | 9.3 | 15.8 |
| US-06 | 26.7 | 22.2 | 20.8 | 19.5 | 22.6 | 24.7 | 13.0 | 18.1 | 22.4 |
| Average | 35.8 | 33.7 | 30.3 | 22.5 | 20.8 | 19.1 | 19.6 | 20.8 | 25.6 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mathew, M.; Mastali, M.; Catton, J.; Samadani, E.; Janhunen, S.; Fowler, M. Development of an Electro-Thermal Model for Electric Vehicles Using a Design of Experiments Approach. Batteries 2018, 4, 29. https://doi.org/10.3390/batteries4020029
Mathew M, Mastali M, Catton J, Samadani E, Janhunen S, Fowler M. Development of an Electro-Thermal Model for Electric Vehicles Using a Design of Experiments Approach. Batteries. 2018; 4(2):29. https://doi.org/10.3390/batteries4020029
Chicago/Turabian StyleMathew, Manoj, Mehrdad Mastali, John Catton, Ehsan Samadani, Stefan Janhunen, and Michael Fowler. 2018. "Development of an Electro-Thermal Model for Electric Vehicles Using a Design of Experiments Approach" Batteries 4, no. 2: 29. https://doi.org/10.3390/batteries4020029





