Viscous Effects on Nonlinear Double Tearing Mode and Plasmoid Formation in Adjacent Harris Sheets
Abstract
:1. Introduction
2. Model Equations
3. Linear DTM Evolution
4. Nonlinear DTM and Plasmoids
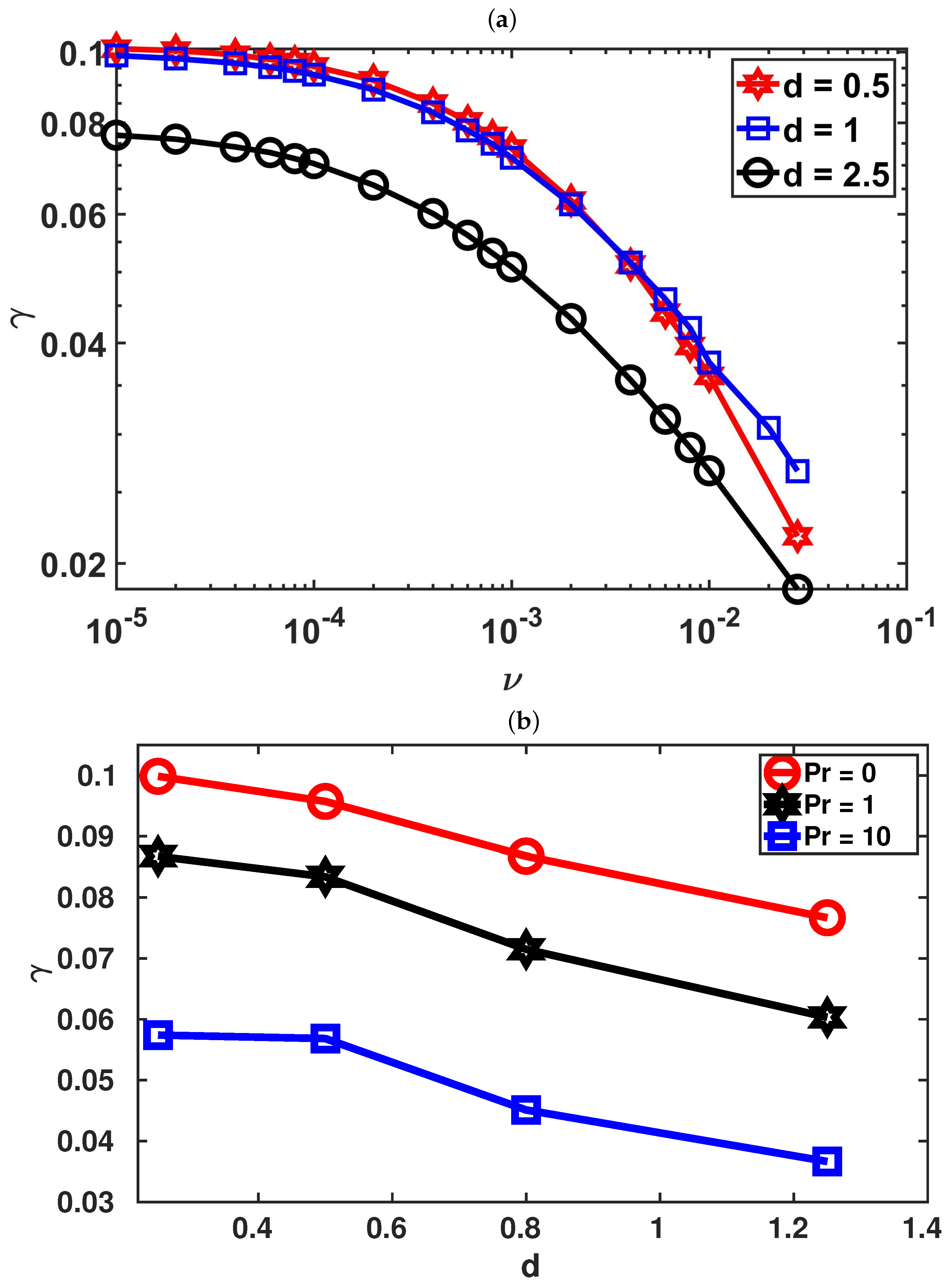
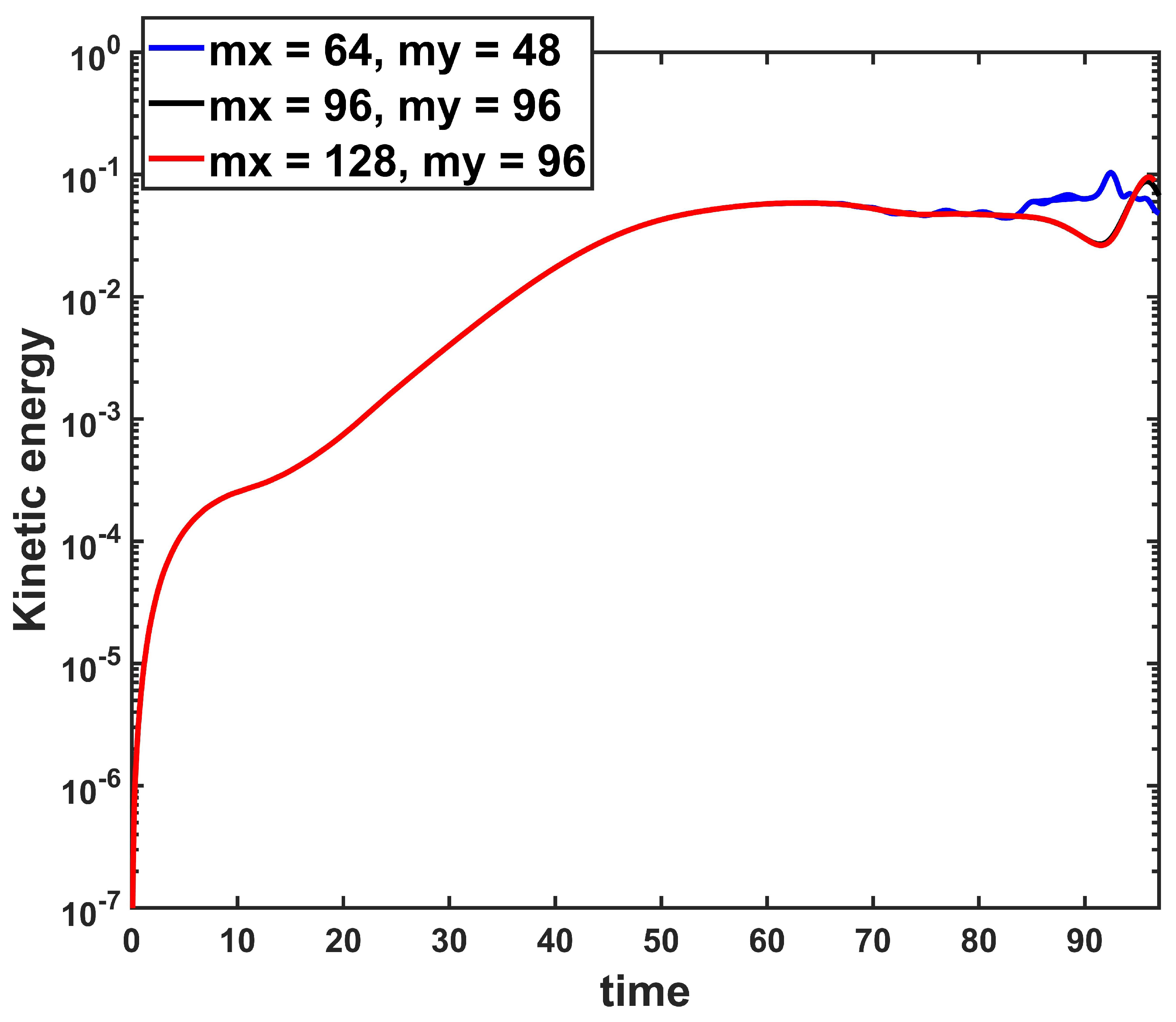
4.1. Nonlinear DTM Evolution
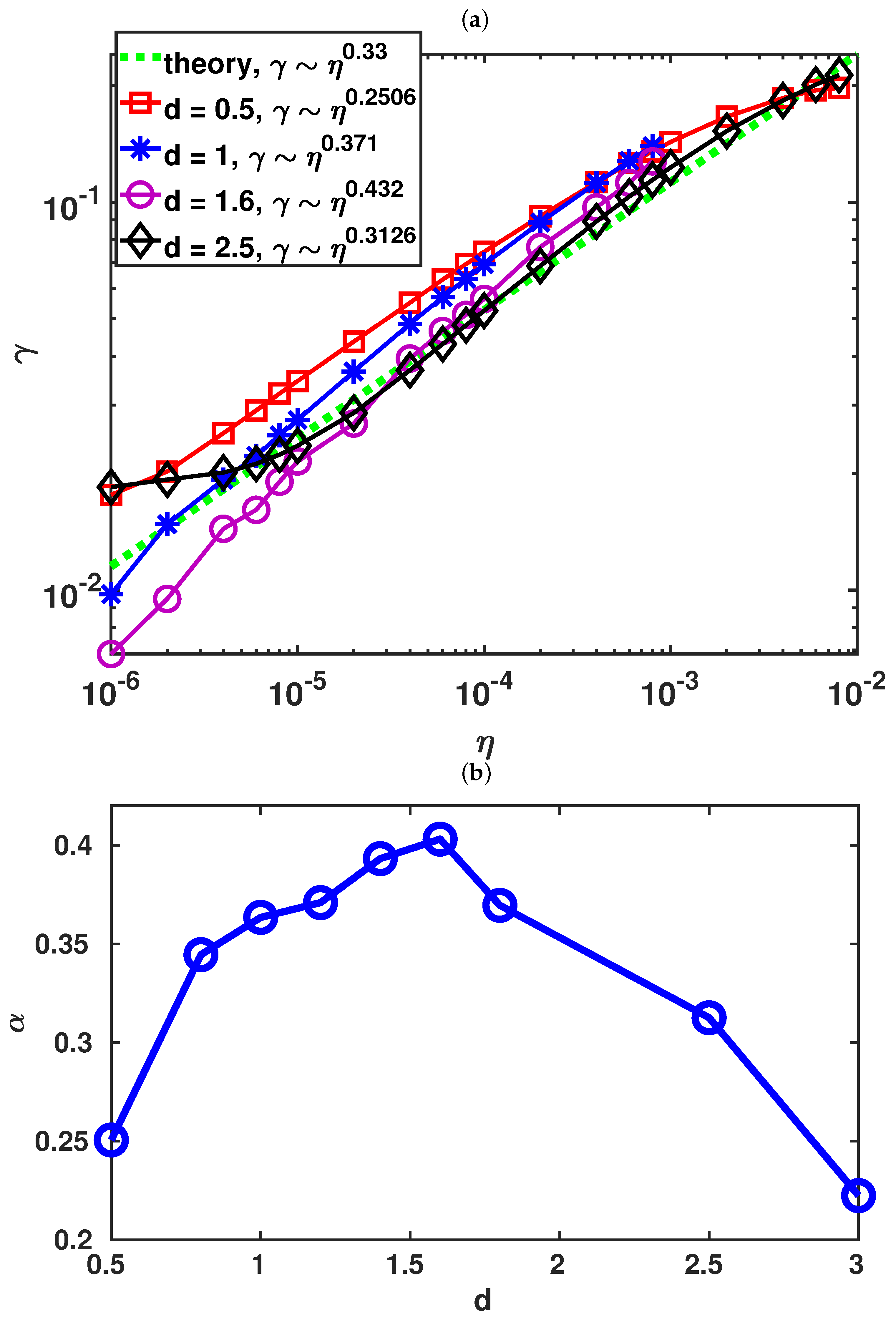
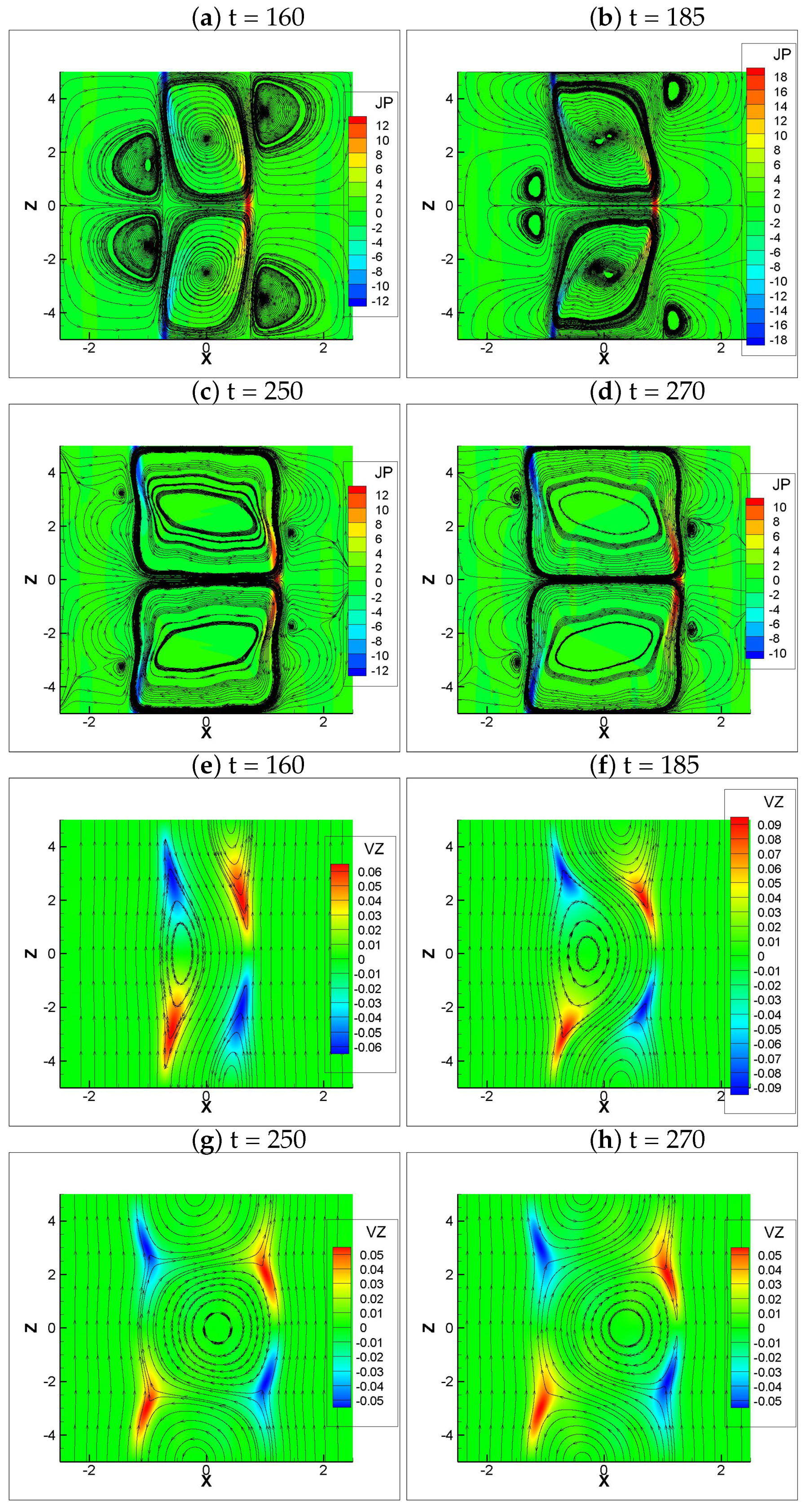
4.2. Plasmoid Formation
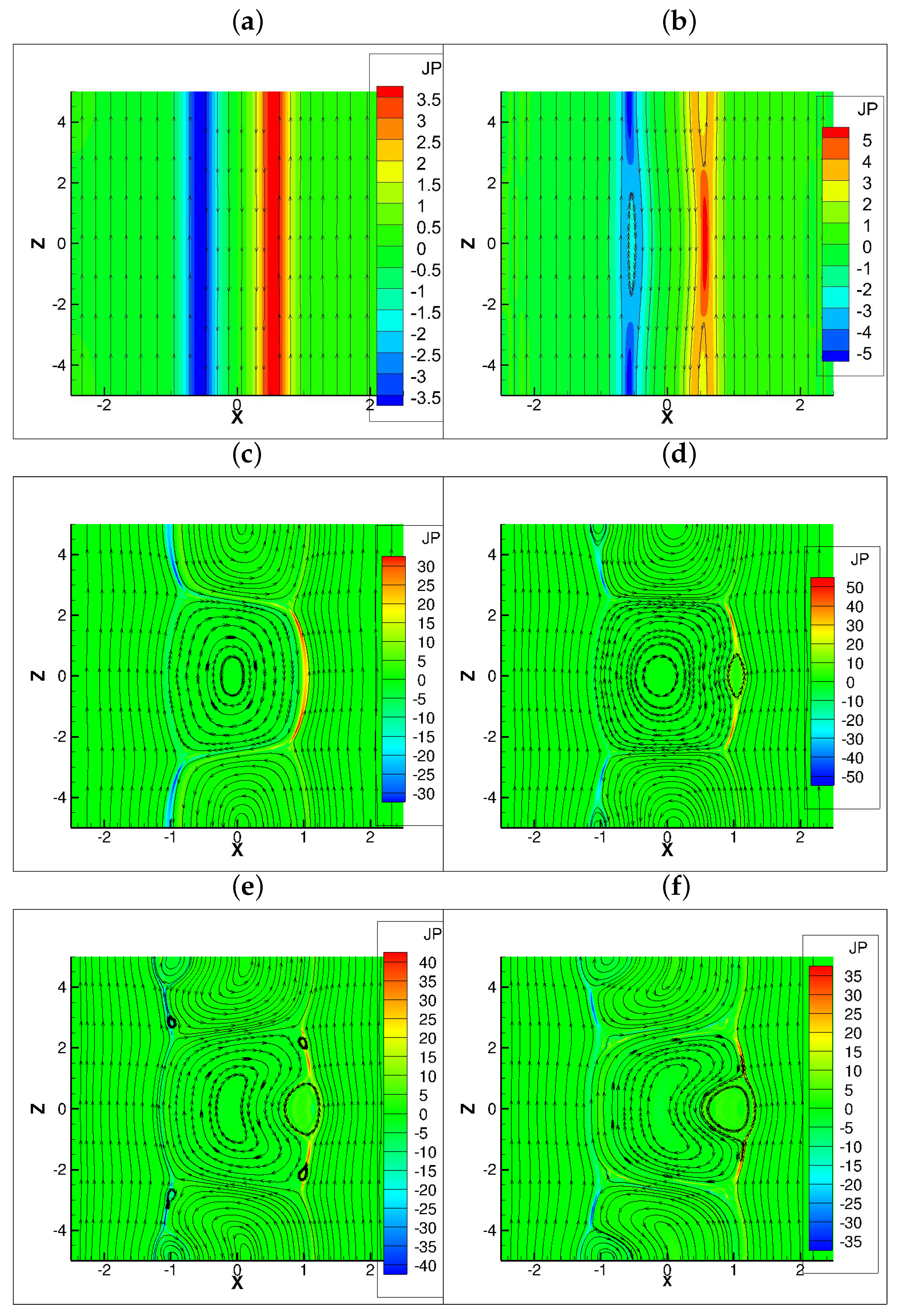
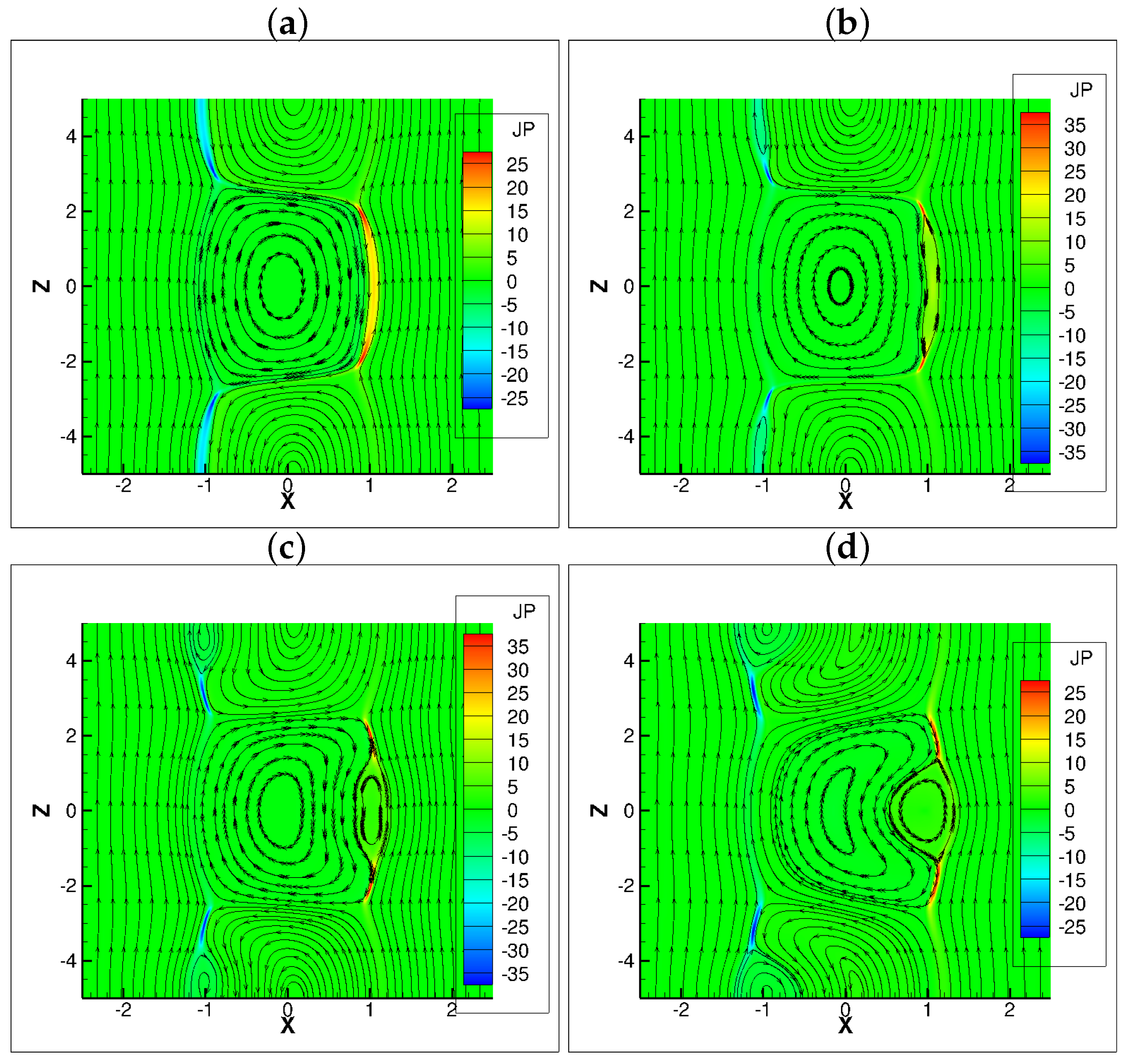
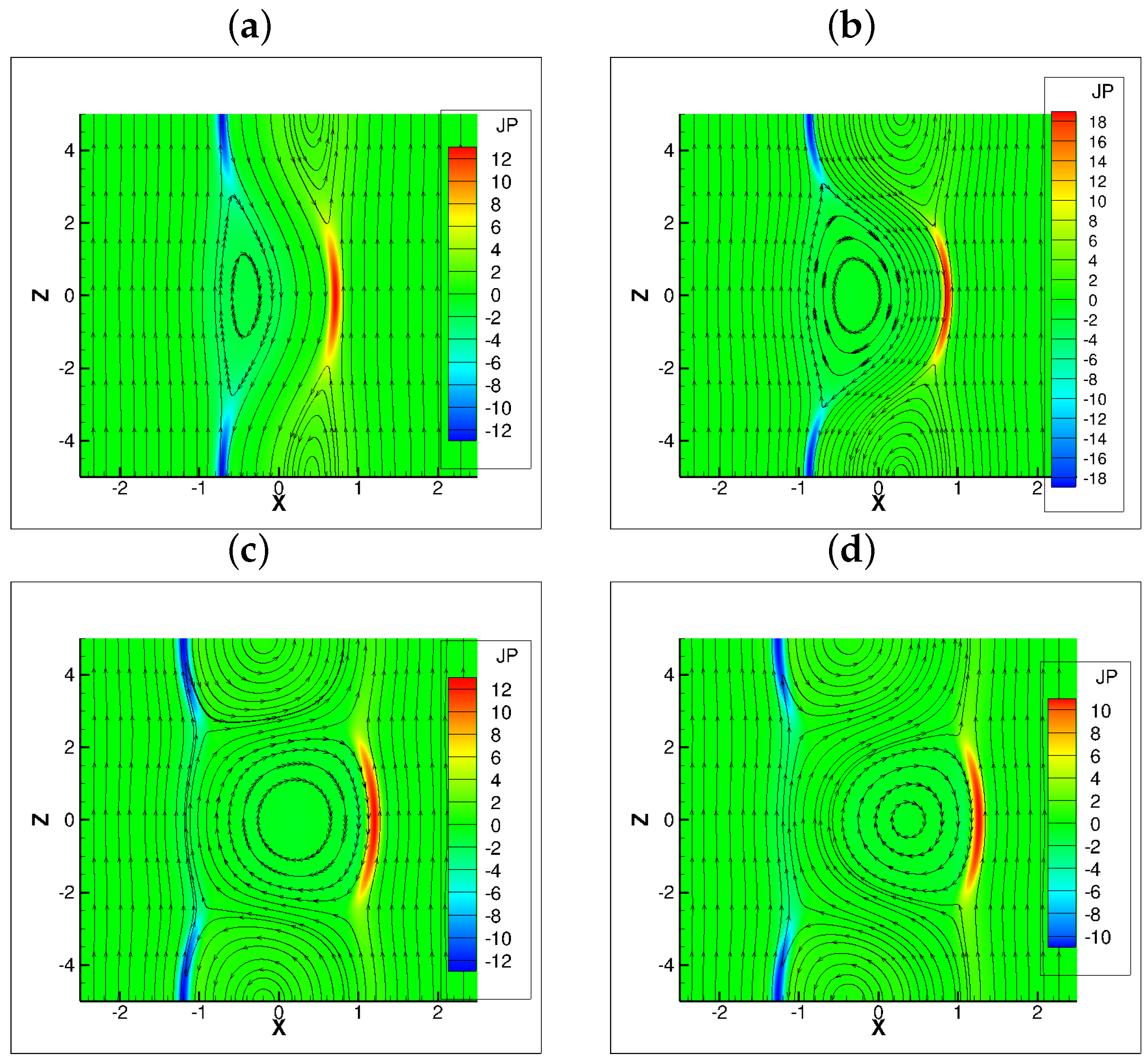
4.3. Flow Pattern and Vortices
5. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bierwage, A.; Benkadda, S.; Hamaguchi, S.; Wakatani, M. Fast growing double tearing modes in a tokamak plasma. Phys. Plasmas 2005, 12, 082504. [Google Scholar] [CrossRef]
- Wang, X.-Q.; Wang, X.; Xu, W.-B.; Wang, Z.-X. Interlocking and nonlinear saturation of double tearing modes in differentially rotating plasmas. Phys. Plasmas 2011, 18, 012102. [Google Scholar] [CrossRef]
- Zweibel, E.G.; Yamada, M. Magnetic Reconnection in Astrophysical and Laboratory Plasmas. Annu. Rev. Astron. Astrophys. 2009, 47, 291. [Google Scholar] [CrossRef]
- Akramov, T.; Baty, H. Non-linear growth of double tearing mode: Explosive reconnection, plasmoid formation, and particle acceleration. Phys. Plasmas 2017, 24, 082116. [Google Scholar] [CrossRef]
- Dahlburg, R.; Karpen, J. A triple current sheet model for adjoining coronal helmet streamers. J. Geophys. Res. Space Phys. 1995, 100, 23489. [Google Scholar] [CrossRef]
- Crooker, N.; Siscoe, G.; Shodhan, S.; Webb, D.; Gosling, J.; Smith, E.J. Multiple heliospheric current sheets and coronal streamer belt dynamics. J. Geophys. Space Phys. 1993, 98, 9371. [Google Scholar] [CrossRef]
- Mikic, Z.; Barnes, D.; Schnack, D. Dynamical evolution of a solar coronal magnetic field arcade. Astrophys. J. 1988, 328, 830. [Google Scholar] [CrossRef]
- Yan, M.; Otto, A.; Muzzell, D.; Lee, L. Tearing mode instability in a multiple current sheet system. J. Geophys. Res. Space Phys. 1994, 99, 8657. [Google Scholar] [CrossRef]
- Bowers, K.; Li, H. Spectral energy transfer and dissipation of magnetic energy from fluid to kinetic scales. Phys. Rev. Lett. 2007, 98, 035002. [Google Scholar] [CrossRef]
- Baty, H. Explosive magnetic reconnection in double-current sheet systems: Ideal versus resistive tearing mode. Astrophys. J. 2017, 837, 74. [Google Scholar] [CrossRef]
- Schwartz, S.J.; Kessel, R.L.; Brown, C.C.; Woolliscroft, L.J.; Dunlop, M.W.; Farrugia, C.J.; Hall, D.S. Active current sheets near the earth’s bow shock. J. Geophys. Space Phys. 1988, 93, 11295. [Google Scholar] [CrossRef]
- Levinton, F.; Zarnstorff, M.; Batha, S.; Bell, M.; Bell, R.; Budny, R.; Bush, C.; Chang, Z.; Fredrickson, E.; Janos, A.; et al. Improved confinement with reversed magnetic shear in tftr. Phys. Rev. Lett. 1995, 75, 4417. [Google Scholar] [CrossRef] [PubMed]
- Ishii, Y.; Azumi, M.; Kishimoto, Y. Structure-driven nonlinear instability of double tearing modes and the abrupt growth after long-time-scale evolution. Phys. Rev. 2002, 89, 205002. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.X.; Wang, X.G.; Dong, J.Q.; Lei, Y.A.; Long, Y.X.; Mou, Z.Z.; Qu, W.X. Fast resistive reconnection regime in the nonlinear evolution of double tearing modes. Phys. Rev. Lett. 2007, 99, 185004. [Google Scholar] [CrossRef]
- Janvier, M.; Kishimoto, Y.; Li, J. Structure-driven nonlinear instability as the origin of the explosive reconnection dynamics in resistive double tearing modes. Phys. Rev. 2011, 107, 195001. [Google Scholar] [CrossRef]
- Priest, E.R. The magnetohydrodynamics of current sheets. Rep. Prog. Phys. 1985, 48, 955. [Google Scholar] [CrossRef]
- Chang, Z.; Park, W.; Fredrickson, E.; Batha, S.; Bell, M.; Bell, R.; Budny, R.; Bush, C.; Janos, A.; Levinton, F.; et al. Off-axis sawteeth and double-tearing reconnection in reversed magnetic shear plasmas in tftr. Phys. Rev. Lett. 1996, 77, 3553. [Google Scholar] [CrossRef]
- Ishii, Y.; Azumi, M.; Kishimoto, Y.; Leboeuf, J. Long timescale plasma dynamics and explosive growth driven by the double tearing mode in reversed shear plasmas. Nucl. Fusion 2003, 43, 539. [Google Scholar] [CrossRef]
- Wang, Z.-X.; Wang, X.; Dong, J.; Kishimoto, Y.; Li, J. Shear flows induced by nonlinear evolution of double tearing modes. Phys. Plasmas 2008, 15, 082109. [Google Scholar] [CrossRef]
- Eriksson, L.-G.; Fourment, C.; Fuchs, V.; Litaudon, X.; Challis, C.D.; Crisanti, F.; Esposito, B.; Garbet, X.; Giroud, C.; Hawkes, N.; et al. Discharges in the JET Tokamak Where the Safety Factor Profile Is Identified as the Critical Factor for Triggering Internal Transport Barriers. Phys. Rev. Lett. 2002, 88, 145001. [Google Scholar] [CrossRef]
- Joffrin, E.; Challis, C.D.; Conway, G.D.; Garbet, X.; Gude, A.; Günter, S.; Hawkes, N.C.; Hender, T.C.; Howell, D.F.; Huysmans, G.T.A.; et al. Internal transport barrier triggering by rational magnetic flux surfaces in tokamaks. Nucl. Fusion 2003, 43, 1167. [Google Scholar] [CrossRef]
- Fredrickson, E.; Bell, M.; Budny, R.V.; Synakowski, E. Nonlinear evolution of double tearing modes in tokamaks. Phys. Plasmas 2000, 7, 4112. [Google Scholar] [CrossRef]
- Dong, J.Q.; Mou, Z.Z.; Long, Y.X.; Mahajan, S.M. Study of internal transport barrier triggering mechanism in tokamak plasmas. Phys. Plasmas 2004, 11, 5673. [Google Scholar] [CrossRef]
- Pritchett, P.; Lee, Y.; Drake, J. Linear analysis of the double-tearing mode. Phys. Fluids 1980, 23, 1368. [Google Scholar] [CrossRef]
- de Baar, M.R.; Hogeweij, G.M.D.; Cardozo, N.J.L.; Oomens, A.A.M.; Schüller, F.C. Electron Thermal Transport Barrier and Magnetohydrodynamic Activity Observed in Tokamak Plasmas with Negative Central Shear. Phys. Rev. Lett. 1997, 78, 4573. [Google Scholar] [CrossRef]
- Maget, P.; Huysmans, G.T.A.; Garbet, X.; Ottaviani, M.; Lütjens, H.; Luciani, J.-F. Nonlinear magnetohydrodynamic simulation of Tore Supra hollow current profile discharges. Phys. Plasmas 2007, 14, 052509. [Google Scholar] [CrossRef]
- Ishii, Y.; Azumi, M.; Kurita, G.; Tuda, T. Nonlinear evolution of double tearing modes. Phys. Plasmas 2000, 7, 4477. [Google Scholar] [CrossRef]
- Günter, S.; Yu, Q.; Lackner, K.; Bhattacharjee, A.; Huang, Y.-M. Fast sawtooth reconnection at realistic Lundquist numbers. Plasma Phys. Control Fusion 2014, 57, 014017. [Google Scholar] [CrossRef]
- Zhang, C.; Ma, Z. Nonlinear evolution of double tearing mode with guiding magnetic field. Phys. Plasmas 2011, 18, 052303. [Google Scholar] [CrossRef]
- Nemati, M.; Wei, L.; Wang, Z. Unstable spectra of double tearing modes with antisymmetric shear flow. Phys. Plasmas 2018, 25, 072119. [Google Scholar] [CrossRef]
- Shen, C.; Liu, Z. Magnetic reconnection processes in multiple current-sheet systems with strong flow shear. Plasma Phys. Control. Fusion 1998, 40, 1. [Google Scholar] [CrossRef]
- Shen, C.; Liu, Z.; Zhang, H. Properties of the resistive instability in double current sheet systems with strong shear flows. Phys. Lett. 1998, 249, 87. [Google Scholar] [CrossRef]
- Nemati, M.; Wang, Z.-X.; Wei, L. Formation of plasmoids in multiple current systems. Astrophys. J. 2016, 821, 128. [Google Scholar] [CrossRef]
- Nemati, M.; Wang, Z.-X.; Wei, L. Dynamics of the plasmoid-unstable regime in different multiple-current plasmas. Astrophys. J. 2017, 835, 191. [Google Scholar] [CrossRef]
- Malara, F.; Veltri, P.; Carbone, V. Competition among nonlinear effects in tearing instability saturation. Phys. Fluids Plasma Phys. 1992, 4, 3070. [Google Scholar] [CrossRef]
- Sarto, D.D.; Ottaviani, M. Secondary fast reconnecting instability in the sawtooth crash. Phys. Plasmas 2017, 24, 012102. [Google Scholar] [CrossRef]
- Loureiro, N.F.; Cowley, S.C.; Dorland, W.D.; Haines, M.G.; Schekochihin, A.A. X-Point Collapse and Saturation in the Nonlinear Tearing Mode Reconnection. Phys. Rev. Lett. 2005, 95, 235003. [Google Scholar] [CrossRef] [PubMed]
- Nemati, M.; Wang, Z.-X.; Wei, L.; Selim, B.I. Plasmoid instability in double current sheets. Phys. Plasmas 2015, 22, 012106. [Google Scholar] [CrossRef]
- Veranda, M.; Cappello, S.; Bonfiglio, D.; Escande, D.F.; Kryzhanovskyy, A. Magnetic reconnection in three-dimensional quasi-helical pinches. Rend. Fis. Acc. Lincei 2020, 31, 963. [Google Scholar] [CrossRef]
- Loureiro, N.F.; Schekochihin, A.A.; Cowley, S.C. Instability of current sheets and formation of plasmoid chains. Phys. Plasmas 2007, 14, 100703. [Google Scholar] [CrossRef]
- Loureiro, N.F.; Samtaney, R.; Schekochihin, A.A.; Uzdensky, D.A. Magnetic reconnection and stochastic plasmoid chains in high-Lundquist-number plasmas. Phys. Plasmas 2012, 19, 042303. [Google Scholar] [CrossRef]
- Uzdensky, D.A.; Loureiro, N.F.; Schekochihin, A.A. Fast Magnetic Reconnection in the Plasmoid-Dominated Regime. Phys. Rev. Lett. 2010, 105, 235002. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.-M.; Bhattacharjee, A. Distribution of Plasmoids in High-Lundquist-Number Magnetic Reconnection. Phys. Rev. Lett. 2012, 109, 265005. [Google Scholar] [CrossRef] [PubMed]
- Guo, W.; Ma, J.; Yu, Z. Multiple secondary islands formation in nonlinear evolution of double tearing mode simulations. Phys. Plasmas 2017, 24, 032115. [Google Scholar] [CrossRef]
- Konovalov, S.; Mikhailovskii, A.; Shirokov, M.; Tsypin, V. Transport threshold model of neoclassical tearing modes in the presence of anomalous perpendicular viscosity. Phys. Plasmas 2002, 9, 4596. [Google Scholar] [CrossRef]
- Kaw, P.K.; Valeo, E.; Rutherford, P.H. Tearing modes in a plasma with magnetic braiding. Phys. Rev. Lett. 1979, 43, 1398. [Google Scholar] [CrossRef]
- Ahmad, N.; Ping, Z.; Ahmad, A.; Shiyong, Z. Viscous effects on plasmoid formation from nonlinear resistive tearing growth in a harris sheet. Plasma Sci. Technol. 2021, 24, 015103. [Google Scholar] [CrossRef]
- Ali, A.; Li, J.; Kishimoto, Y. On the magnetic reconnection of resistive tearing mode with the dynamic flow effects. Phys. Plasmas 2015, 22, 042102. [Google Scholar] [CrossRef]
- Ali, A.; Zhu, P. Effects of plasmoid formation on sawtooth process in a tokamak. Phys. Plasmas 2019, 26, 052518. [Google Scholar] [CrossRef]
- Aydemir, A. Magnetohydrodynamic modes driven by anomalous electron viscosity and their role in fast sawtooth crashes. Phys. Fluids Plasma Phys. 1990, 2, 2135. [Google Scholar] [CrossRef]
- Dong, J.Q.; Mahajan, S.; Horton, W. Double tearing mode in plasmas with anomalous electron viscosity. Phys. Plasmas 2003, 10, 3151. [Google Scholar] [CrossRef]
- Sovinec, C.; Glasser, A.; Gianakon, T.; Barnes, D.; Nebel, R.; Kruger, S.; Schnack, D.; Plimpton, S.; Tarditi, A.; Chu, M.; et al. Nonlinear magnetohydrodynamics simulation using high order finite elements. J. Comput. Phys. 2004, 195, 355. [Google Scholar] [CrossRef]
- He, Z.; Dong, J.Q.; He, H.; Wang, Z.T.; Long, Y.X.; Mou, Z.Z. Study of nonlinear evolution of tearing modes induced by anomalous electron viscosity. Phys. Scr. 2015, 90, 125603. [Google Scholar] [CrossRef]
- Mao, A.; Wang, Z.; He, X.; Wang, X. Nonlinear evolution and secondary island formation of the double tearing mode in a hybrid simulation. Plasma Sci. Technol. 2021, 23, 035103. [Google Scholar] [CrossRef]
- Takeda, K. Nonlinear viscoresistive dynamics of the m=1 tearing instability. Phys. Plasmas 2008, 15, 022502. [Google Scholar] [CrossRef]
- Wei, L.; Yang, X.; Zheng, S.; Liu, Y. Numerical study of collisionless q = 1 tearing instability in a cylindrical plasma. J. Plasma Phys. 2012, 78, 663. [Google Scholar] [CrossRef]
- Bierwage, A.; Benkadda, S.; Hamaguchi, S.; Wakatani, M. Dynamics of resistive double tearing modes with broad linear spectra. Phys. Plasmas 2007, 14, 022107. [Google Scholar] [CrossRef]
- Ofman, L. Double tearing instability with shear flow. Phys. Fluids Plasma Phys. 1992, 4, 2751. [Google Scholar] [CrossRef]
- Ali, A.; Li, J.; Kishimoto, Y. On the abrupt growth dynamics of nonlinear resistive tearing mode and the viscosity effects. Phys. Plasmas 2014, 21, 052312. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmad, N.; Zhu, P.; Shen, C.; Ali, A.; Zeng, S. Viscous Effects on Nonlinear Double Tearing Mode and Plasmoid Formation in Adjacent Harris Sheets. Magnetochemistry 2023, 9, 205. https://doi.org/10.3390/magnetochemistry9090205
Ahmad N, Zhu P, Shen C, Ali A, Zeng S. Viscous Effects on Nonlinear Double Tearing Mode and Plasmoid Formation in Adjacent Harris Sheets. Magnetochemistry. 2023; 9(9):205. https://doi.org/10.3390/magnetochemistry9090205
Chicago/Turabian StyleAhmad, Nisar, Ping Zhu, Chao Shen, Ahmad Ali, and Shiyong Zeng. 2023. "Viscous Effects on Nonlinear Double Tearing Mode and Plasmoid Formation in Adjacent Harris Sheets" Magnetochemistry 9, no. 9: 205. https://doi.org/10.3390/magnetochemistry9090205




