The Microscopic Mechanisms Involved in Superexchange
Abstract
:1. Introduction
- J is expressed vs. fundamental molecular integrals in the absence of a crystal field, uniquely, for the sake of simplicity; we show that the introduction of a crystal field may be achieved very easily, thus allowing us to discuss further the notion of anisotropic couplings;
- For the first time, we may rigorously predict the ferromagnetic (J < 0) or antiferromagnetic (J > 0) character of spin-spin couplings whereas, so far, we have dealt with empirical rules, i.e., the Goodenough–Kanamori rules published between the middle of the 1950s and the beginning of the 1960s [11,12,13,14].
- Here, without a crystal field, we deal with a theoretical model, from which we derive the conclusion that when coulombic interactions are dominant, our model follows Hund’s rule and we explain why couplings are automatically ferromagnetic; when coulombic interactions are no longer dominant, our model is equivalent to the molecular orbital one and couplings are always antiferromagnetic (except in a particular case, where couplings are ferromagnetic but present a small absolute value of J);
- By introducing the notion of a crystal field, we discuss how passing from an isotropic (Heisenberg) coupling to an anisotropic one (z-z, i.e., an Ising-like coupling or an x-y one); in addition, from the theoretical expression of J, we may also predict the ferromagnetic (J < 0) or antiferromagnetic (J > 0) character of spin-spin couplings as in the absence of a crystal field, which is the key finding of this article.
2. Microscopic Mechanisms Involved in Superexchange
2.1. Basic Physical Considerations
2.1.1. Generalities and Hund’s Rules
2.1.2. The First “Historical” Model Proposed by Anderson for Superexchange
- The direct overlap of the involved wave functions characterizing the pair of magnetic sites A and B separated by the non-magnetic ligand X vanishes;
- The ligand wave function is weakly modified by the presence of magnetic ions;
- This modification confers a magnetic character that is the origin of the exchange interactions between the pair of magnetic ions through the non-magnetic ligand.
- Experimental measurements confirmed the transfer while examining the hyperfine interaction between the ligand nuclear spin and that of the magnetic ion;
- It has been graphically demonstrated that the ligand wave function is partially magnetic with the expected degrees;
- The electronic transfer of the up (or down) spin of ligand X to the empty left (or right) d orbital must remain ballistic, i.e., it conserves the spin so that it leads to an antiferromagnetic coupling;
2.2. Starting Assumptions
2.2.1. Assumption 1
2.2.2. Assumption 2
 . As we deal with a two-electron problem on both sides of ligand X, separately, the two low-lying states of the bonds A–X and X–B are a spin-singlet and a spin-triplet. Indeed, if the spin wave function χ(s1,s2) =|s1,s2> =|s1>⊗|s2> = |>⊗|> = |,> describes the spin states, we have four possible pairings: |↑↑>,|↑↓>, |↓↑> and |↓↓>. If S = s1 + s2, we have two classes of possibilities for writing the spin wave function:
. As we deal with a two-electron problem on both sides of ligand X, separately, the two low-lying states of the bonds A–X and X–B are a spin-singlet and a spin-triplet. Indeed, if the spin wave function χ(s1,s2) =|s1,s2> =|s1>⊗|s2> = |>⊗|> = |,> describes the spin states, we have four possible pairings: |↑↑>,|↑↓>, |↓↑> and |↓↓>. If S = s1 + s2, we have two classes of possibilities for writing the spin wave function:
- |0, 0> =(|↑↓> − |↓↑>), S = 0 (singlet state),
- S = 1 (triplet state).
2.2.3. Assumption 3
 ) = 0 (where 1 is the identity matrix and H = T1 + T2 + U(r1,r2)) can be solved (cf. Equation (1)). The solutions are spatially symmetric and antisymmetric wave functions, i.e., , with <ΦS(r1,r2)|ΦA(r1,r2)> = 0 by construction.
) = 0 (where 1 is the identity matrix and H = T1 + T2 + U(r1,r2)) can be solved (cf. Equation (1)). The solutions are spatially symmetric and antisymmetric wave functions, i.e., , with <ΦS(r1,r2)|ΦA(r1,r2)> = 0 by construction.2.2.4. Assumption 4
- S = 0 χ(s1,s2) = |s1,s2> odd, Φ(r1,r2) = ΦS(r1,r2) even,
- S = 1 χ(s1,s2) = |s1,s2> even, Φ(r1,r2) = ΦA(r1,r2) odd.
2.2.5. Assumption 5
2.2.6. Assumption 6
2.2.7. Assumption 7
2.2.8. Assumption 8
- The states are normalized but not orthogonal (except |A> and |B>):
- The overlap between A and X on the one hand, and X and B on the other one, are defined as follows:
- Both magnetic sites A and B have a cationic energy level higher than the anionic one, as is generally the case for transition metal compounds; the energy difference between A and X levels (respectively, X and B levels) is 2δAEA, with EA > 0 (respectively, 2δBEB, with EB > 0), so that we have for the fragment A–X linked to X–B:
<X|(T2 + V2)|X> = − (1 + δA)EA, EA > 0, <X|(T3 + V3)|X> = − (1 + δB)EB, EB > 0¸ A ≠ B,
<A|(T1 + V1)|A> = <B|(T4 + V4)|B> = − (1 − δ)E,
<X|(T2 + V2)|X> = <X|(T3 + V3)|X> = − (1 + δ)E, E > 0, A = B.
- The transfer integrals between |A> and |X> on the one hand, and |X> and |B> on the other hand, are given by:
- sA, tAX and tXB are small compared to unity, and tAX or tXB is mainly related to the potential interaction between the anion and the cation, so that:
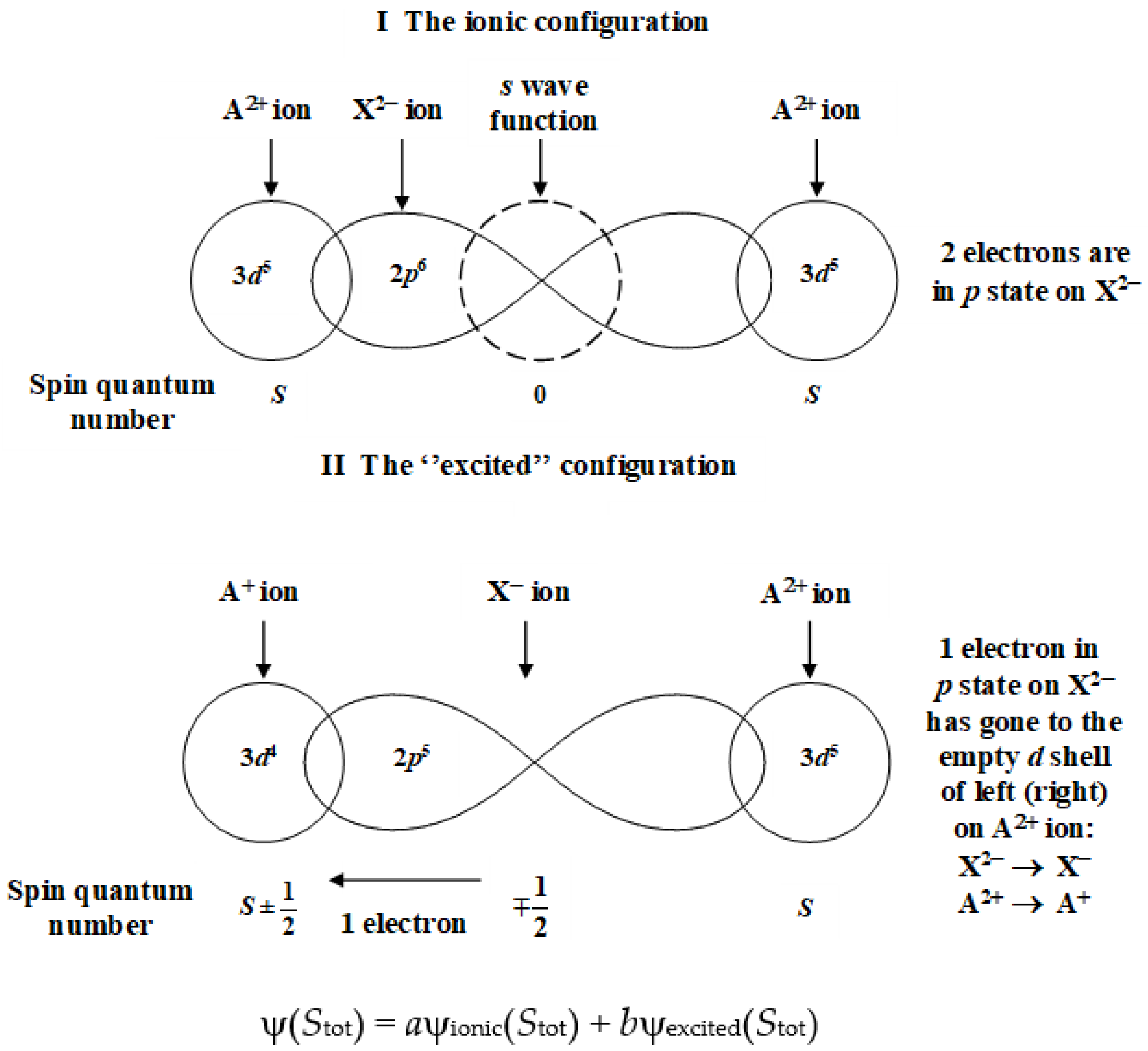
2.3. Expression of the Intermediate “Cationic” States
- The first rule consists of treating the extra electrons in terms of the simple one-electron Hartree–Fock functions;
- The second rule is treating them as excitations of a many-body system; this operation is achieved while keeping a constant value for the total spin involved, Stot; this leads us to consider an ionic part for centers A and B and an excited one for the ligand X;
- As we deal with weak energies involved in the process of excitation, the orbital part ψ(Stot) may be written as the following hybridization: ψ(Stot) = aψionic(Stot) + bψexcited(Stot), where the coefficients a and b must remain small.
2.4. Construction of the Collective States
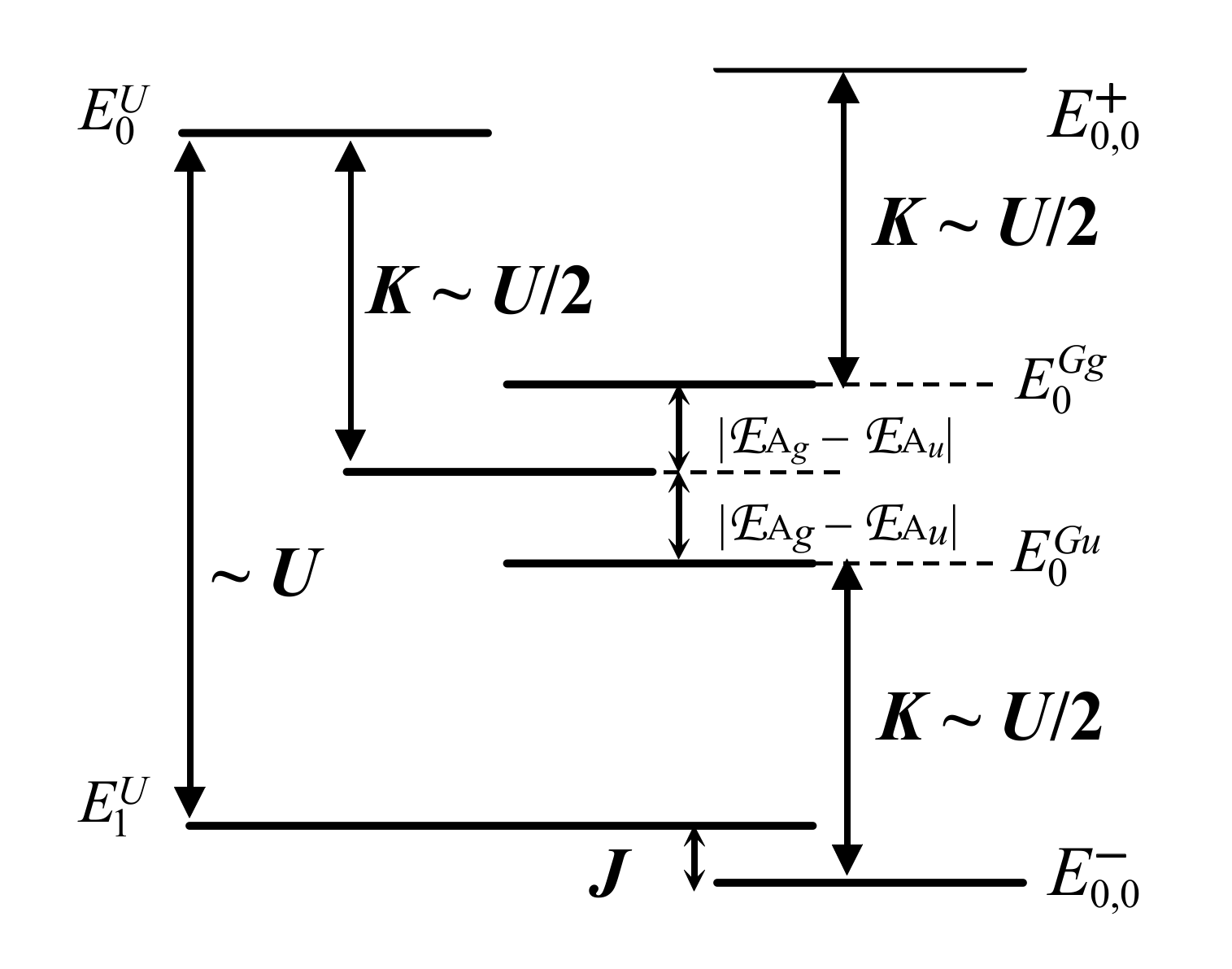
2.5. The Hamiltonian Matrix and Energy Spectrum
- Diagonal and off-diagonal terms between |> and |>;
- Only diagonal terms for the states |US,SZ > with S = 0 (Sz = 0) and S = 1 (Sz = 0, ±1);
- All the diagonal terms of the states |U1,SZ > are equal because we deal with the irrep Γ1⊗Γ3,u. Under these conditions, the Hamiltonian matrix is:
- U is the Coulomb energy for an electron pair occupying the same site;
- C is the Coulomb energy for two electrons occupying neighboring sites;
- γ1 is the Coulomb self-energy of the exchange charge distribution −eΦA(r)ΦB(r) and is, thus, referred to as the exchange integral;
- γ2 appears as the Coulomb energy between the exchange charge distribution and an electron charge localized on one site. γ2 is a transfer integral between two cationic orbitals, resulting from the effective coulombic potential created by the charge of another electron involved in the secular problem;
- When there is no superexchange, i.e., no exchange between A and B through X, we have γ1 ≠ 0 (the exchange charge distribution is restricted to the bond between A and X, X and B), γ2 = 0 as there are no more cationic orbitals and U ≠ 0, C ≠ 0 (the Coulomb energy for two electrons is restricted to first neighboring sites: A and X or X and B).
3. Physical Interpretation
3.1. Expression of Jm,m′
- The states |US,Sz > with S = 1 (Sz = 0, ±1) that are associated with a “triplet state”, characterized by the eigenvalues and (three-times degenerated); and
- The states |> and |> , with S = 0, are associated with a “singlet state”, characterized by the eigenvalues .
- Jm,m′ = ES,0 – ET,0 with the corresponding Hamiltonian exchange Hex = −Jm,m′s1.s2 (convention 1); in that case, J < 0 corresponds to an antiferromagnetic arrangement, with ET,0 > ES,0, whereas J > 0 corresponds to a ferromagnetic one, with ET,0 < ES,0, where m and m′ are the name of d bands located on each side of the ligand X.
- Jm,m′ = ET,0 – ES,0 with the corresponding Hamiltonian exchange Hex = Jm,m′s1.s2 (convention 2); in that case, J > 0 corresponds to an antiferromagnetic arrangement, with ET,0 > ES,0, whereas J < 0 corresponds to a ferromagnetic one, also with ET,0 < ES,0.
- J << Δ
- kBT << Δ
- Case 1: (see Figure 4).
- Case 2: (see Figure 5).
3.2. Physical Comments Regarding the Sign of J
3.2.1. Hund’s First Rule
3.2.2. Molecular Orbital Model
3.3. Superexchange Hamiltonian for a 3d1 ion. Generalization to an ndm ion (3 ≤ n ≤ 5, 1 ≤ m ≤ 10)
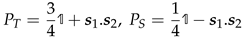
 is the 4 × 4 identity matrix. Under these conditions, it is easy to show:
is the 4 × 4 identity matrix. Under these conditions, it is easy to show:3.4. Introduction of Crystal Field Theory
3.4.1. Expression of Jm,m′; Physical Discussion of the Crystal Field Effect
- Case 1: .
- ; we deal with a weak CF contribution (in the case of 3dm ions); ; the surrounding cage is mainly characterized by an important geometrical size: we may deal with Class I compounds. This is also the case when using organic ligands whose long length may be adapted to the magnetic system that one wishes to build up [15,16,17,18]; this is a good way to obtain isotropic (Heisenberg) spin-spin couplings for Class II compounds; we always have ferromagnetic couplings, including in the particular case of so that, finally, the ferromagnetic coupling is strongly enhanced and (in the case of ions 4dm and 5dm);
- ; we deal with a strong CF contribution (case of 5dm ions); now we have ; antiferromagnetic couplings are favored and this only concerns Class I compounds.
- Case 2:
3.4.2. Expression of the Hamiltonian
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A
- The charges composing the cage are located at the corners of an octahedron (sixfold coordination); in that case, Rk = (a,0,0), (−a,0,0), (0,a,0), (0,−a,0), (0,0,a) and (0,0,−a); Rk = a is the distance of each corner from the origin;
- The charges are located at the corners of a cube (eightfold coordination); Rk = (a,a,a), (−a,a,a), (a,−a,a), (−a,−a, a), (a,−a,−a), (a,a,−a), (−a, a,−a) and (−a,−a,−a);;
- The charges are located at the corners of a tetrahedron (with two tetrahedra per cube, fourfold coordination); Rk = (a,a,a), (−a,−a,a), (a,−a,−a), (−a,a,−a) for tetrahedron 1 and Rk = (a,−a,a), (−a,a,a), (−a,−a, −a), (a,a,−a) for tetrahedron 2;.
References
- Anderson, P.W. Antiferromagnetism. Theory of superexchange interaction. Phys. Rev. 1950, 79, 350. [Google Scholar] [CrossRef]
- Anderson, P.W. New approach to the theory of superexchange interactions. Phys. Rev. 1959, 115, 2. [Google Scholar] [CrossRef]
- Anderson, P.W. Theory of magnetic exchange interactions: Exchange in insulators and semiconductors. Solid State Phys. 1963, 14, 99. [Google Scholar]
- Anderson, P.W. Magnetism; Rado, G.T., Suhl, H., Eds.; Wiley: New York, NY, USA, 1962; Volume I, p. 25. [Google Scholar]
- Kanamori, J. Theory of the magnetic properties of ferrous and cobaltous oxides, I. Prog. Theor. Phys. 1957, 17, 177. [Google Scholar] [CrossRef] [Green Version]
- Kanamori, J. Theory of the magnetic properties of ferrous and cobaltous oxides, II. Prog. Theor. Phys. 1957, 17, 197. [Google Scholar] [CrossRef] [Green Version]
- Van Vleck, J.H. Note on the use of the Dirac vector model in magnetic materials. Rev. Mat. Fis. Teor. 1962, 14, 189. [Google Scholar]
- Levy, P.M. Rare-earth-iron exchange interaction in the garnets. I. Hamiltonian for anisotropic exchange interaction. Phys. Rev. 1964, 135, A155. [Google Scholar] [CrossRef]
- Levy, P.M. Rare-earth-iron exchange interaction in the garnets. II. Exchange Potential for Ytterbium. Phys. Rev. 1966, 147, 311. [Google Scholar] [CrossRef]
- Curély, J. Magnetic orbitals and mechanisms of exchange. II. Superexchange. Mon. Für Chem. 2005, 136, 1013. [Google Scholar] [CrossRef]
- Goodenough, J.B. Direct cation-cation interactions in several oxides. Phys. Rev. 1960, 117, 1442. [Google Scholar] [CrossRef]
- Goodenough, J.B. Theory of the role of covalence in the perovskite-type manganites [La,M(II)]MnO3. Phys. Rev. 1955, 100, 564. [Google Scholar] [CrossRef] [Green Version]
- Goodenough, J.B. An interpretation of the magnetic properties of the perovskite-type mixed crystals La1−xSrxCoO3−λ. J. Phys. Chem. Solids 1958, 6, 287. [Google Scholar] [CrossRef]
- Kanamori, J. Superexchange interaction and symmetry properties of electron orbitals. J. Phys. Chem. Solids 1959, 10, 87. [Google Scholar] [CrossRef]
- Escuer, A.; Vicente, R.; Goher, M.A.S.; Mautner, F.A. Synthesis and structural characterization of [Mn(ethyl isonicotinate)2(N3)2]n, a two-Dimensional alternating ferromagnetic-antiferromagnetic compound. Magnetostructural correlations for the end-to-end pseudohalide-manganese system. Inorg. Chem. 1996, 35, 6386. [Google Scholar] [CrossRef]
- Escuer, A.; Vicente, R.; Goher, M.A.S.; Mautner, F.A. A new two-dimensional manganese(II)-azide polymer. Synthesis, structure and magnetic properties of [{Mn(minc)2(N3)2}]n (minc = methyl isonicotinate). J. Chem. Soc. Dalton Trans. 1997, 22, 4431. [Google Scholar] [CrossRef]
- Goher, M.A.S.; Morsy, A.M.A.-Y.; Mautner, F.A.; Vicente, R.; Escuer, A. Superexchange interactions through quasi-linear end-to-end azido bridges: Structural and magnetic characterisation of a new two-dimensional manganese-azido system [Mn(DENA)2(N3)2]n (DENA = diethylnicotinamide). Eur. J. Inorg. Chem. 2000, 8, 1819. [Google Scholar] [CrossRef]
- Escuer, A.; Esteban, J.; Perlepes, S.P.; Stamatatos, T.C. The bridging azido ligand as a central “player” in high-nuclearity 3d-metal cluster chemistry. Coord. Chem. Rev. 2014, 275, 87, and references therein. [Google Scholar] [CrossRef]
- Shull, C.G.; Strauser, W.A.; Wollan, E.O. Neutron diffraction by paramagnetic and antiferromagnetic substances. Phys. Rev. 1951, 83, 333. [Google Scholar] [CrossRef]
- Tinkham, M. Paramagnetic resonance in dilute iron group fluorides. I. Fluorine hyperfine structure. Proc. R. Soc. 1956, A236, 535. [Google Scholar]
- Shulman, R.G.; Jaccarino, V. Effects of superexchange on the nuclear magnetic resonance of MnF2. Phys. Rev. 1956, 103, 1126. [Google Scholar] [CrossRef]
- Jaccarino, V.; Shulman, R.G. Observation of nuclear magnetic resonance in antiferromagnetic Mn(F19)2. Phys. Rev. 1957, 107, 1196. [Google Scholar] [CrossRef]
- Shulman, R.G.; Jaccarino, V. Nuclear magnetic resonance in paramagnetic MnF2. Phys. Rev. 1957, 108, 1219. [Google Scholar] [CrossRef]
- Kondo, J. Band theory of superexchange interaction. Prog. Theor. Phys. 1957, 18, 541. [Google Scholar] [CrossRef] [Green Version]
- Blount, E.I. Formalisms of band theory. Solid State Phys. 1962, 13, 305. [Google Scholar]
- Jahn, H.A.; Teller, E. Stability of polyatomic molecules in degenerate electronic states-I—Orbital degeneracy. Proc. Roy. Soc. 1937, A161, 220. [Google Scholar]
- Bates, C.A. Jahn-Teller effects in paramagnetic crystals. Phys. Rep. 1978, 35, 187. [Google Scholar] [CrossRef]
- Kahn, O. Magneto-Structural Correlations in Exchange Coupled Systems; Willett, R.D., Gatleschi, D., Kahn, O., Eds.; NATO ASI Series, Series C: Mathematical and Physical Sciences; Reidel Publishing Company: Dordrecht, The Netherlands, 1985; Volume 140, p. 37. [Google Scholar]
- Kahn, O. Molecular Magnetism; VCH Publishers: New York, NY, USA, 1993. [Google Scholar]
- Girerd, J.J.; Journaux, Y.; Kahn, O. Natural or orthogonalized magnetic orbitals: Two alternative ways to describe the exchange interaction. Chem. Phys. Lett. 1981, 82, 534. [Google Scholar] [CrossRef]
- Curély, J. Magnetic orbitals and mechanisms of exchange. I. Direct exchange. Special Issue. Mon. Für Chem. 2005, 136, 987. [Google Scholar]
- Van Vleck, J.H. Theory of the variations in paramagnetic anisotropy among different salts of the iron group. Phys. Rev. 1932, 41, 208. [Google Scholar] [CrossRef]
- Moriya, T. Magnetism; Rado, G.T., Suhl, H., Eds.; Wiley: New York, NY, USA, 1962; Volume I, p. 85. [Google Scholar]
- Moriya, T. Anisotropic superexchange interaction and weak ferromagnetism. Phys. Rev. 1960, 120, 91. [Google Scholar] [CrossRef]
- Dzialoshinskii, I.E. Thermodynamic theory of “weak” ferromagnetism in antiferromagnetic substance. Sov. Phys. JETP 1957, 6, 1259. [Google Scholar]
- Dzialoshinskii, I.E. A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics. J. Phys. Chem. Solids 1958, 4, 241. [Google Scholar] [CrossRef]
- Katsnelson, M.I.; Kvashnin, Y.O.; Mazurenko, V.V.; Lichtenstein, A.I. Correlated band theory of spin and orbital contributions to Dzialoshinskii-Moriya interactions. Phys. Rev. 2010, 82, 100403. [Google Scholar] [CrossRef] [Green Version]
- Qi, X.; Guionneau, P.; Lafon, E.; Pérot, S.; Kaufmann, B.; Mathonière, C. New photomagnetic ionic salts based on [MoIV(CN)8] 4− and [WIV(CN)8]4− anions. Magnetochemistry 2021, 7, 97. [Google Scholar] [CrossRef]
- Varshalovich, D.A.; Moskalev, A.N.; Kherkonskii, V.K. Quantum Theory of Angular Momentum; World Scientific: Singapore; Teaneck, NJ, USA; Hong Kong, China, 1988; p. 166. [Google Scholar]
- Hutchings, M.T. Point-charge calculations of energy levels of magnetic ions in crystalline electric fields. Solid State Phys. 1964, 16, 227. [Google Scholar]
- Edmonds, A.R. Angular Momentum in Quantum Mechanics; Princeton University Press, Ed.; Princeton University Press: Princeton, NJ, USA, 1957. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Curély, J. The Microscopic Mechanisms Involved in Superexchange. Magnetochemistry 2022, 8, 6. https://doi.org/10.3390/magnetochemistry8010006
Curély J. The Microscopic Mechanisms Involved in Superexchange. Magnetochemistry. 2022; 8(1):6. https://doi.org/10.3390/magnetochemistry8010006
Chicago/Turabian StyleCurély, Jacques. 2022. "The Microscopic Mechanisms Involved in Superexchange" Magnetochemistry 8, no. 1: 6. https://doi.org/10.3390/magnetochemistry8010006




