Modeling and Experimental Study on Drying Characteristics of Corn Particles with Hot Air in Downward Moving Bed
Abstract
:1. Introduction
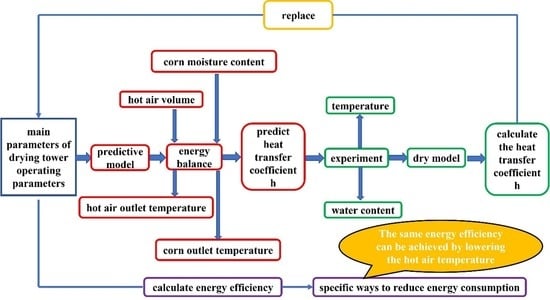
2. Model Development
2.1. Basic Properties of Corn Particle
2.2. Drying System
2.3. Heat Balance Calculation of Drying Tower
3. Experimental Test of Convective Heat Transfer Coefficient
3.1. Experimental System
3.2. Heat Transfer Model of Hot Air Drying Corn Particles
Conservation Equation
- Energy equation for corn particles
- (1)
- Heat transfer to corn:where h is the convective heat transfer coefficient, ; Sbed* is the convection heat transfer area, which is the effective surface area of corn, m2; Tgas is the hot air temperature, K; and Tbed is the initial temperature of corn, K.
- (2)
- Energy needed to evaporate moisture from the corn into the hot air:where msteam represents the mass of moisture from the particles to the hot air in unit time, kg; Cw is the specific heat at this temperature, ; Cυ is the specific heat of moisture vapor at this tempature, ; and rh is the latent heat of evaporation of moisture at this temperature, .
- 2.
- Energy balance of dry hot air
- 3.
- Mass conservation equation
3.3. Calculate the Convective Heat Transfer Coefficient
4. Energy Efficiency Calculation of Drying Tower
5. Conclusions
- (1)
- A heat balance model was established to describe the heating process of fresh corn in the downward moving tower with hot air, which has a very important guiding significance for the improvement of the energy efficiency of the drying system.
- (2)
- To determine the convective heat transfer coefficient between the fresh corn and hot air, a corn particle drying system with hot air was established, and the effects of hot air temperature and wind speed were discussed. Utilizing the heat balance model, the total convective heat transfer coefficients were determined in the range of 39.4–53.8 W/m2·K.
- (3)
- Utilizing the convective heat transfer coefficient of 46.7 W/m2·K, the drying energy efficiency in different drying zones in the drying tower was calculated and verified with the operation data. The highest efficiency of the first drying zone was 60.15% due to the high inlet temperature of hot air. When the hot air temperature in the second drying zone is 140 °C, the energy efficiency is only 41.97%. It is recommended that if the inlet hot air temperature can be reduced to 135 °C, then the energy efficiency will be increased to 45%.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclatures
| A | m2 |
| Cp | Specific heat capacity of moisture (kJ/kg K) |
| Cp-coal | Specific heat of dry corn (J/kg K) |
| Cp, p | Corn particle specific heat capacity at constant pressure (kJ/kg K) |
| Cv | Specific heat of moisture vapor at this temperature (J\kg K) |
| Cw | Specific heat at this temperature (J/kg K) |
| Dy | Moisture diffusion coefficient, kg/(m2 · s) |
| h | Convective heat transfer coefficient (W/m2 K) |
| L | Height of the drying section (m) |
| m | Moisture evaporation (kg/s) |
| md | Relative dry material mass (g) |
| mw | Wet component mass of wet material (g) |
| rh | Latent heat of evaporation of moisture at this temperature (J/kg) |
| Sbed* | Convection heat transfer area (m2) |
| Tbed | Initial temperature of corn (K) |
| Tbed out | Export temperature of corn (°C) |
| Tbed x | Central temperature of corn particles |
| Tgas | Hot air temperature (K) |
| Tgas in | Inlet temperature of hot air (°C) |
| Tgas out | Outlet temperature of hot air (°C) |
| Y* | Critical moisture content of corn particles (%) |
| Yw-bed | Whole average moisture content of corn (%) |
| Yw-gas | Moisture content of the hot air (%) |
References
- Krissada, N.; Phitsanupong, P.; Witaya, P. Thermal analysis of hot air drying of chicken manure pellets in a modified portable horizontal rotary dryer. Heat Mass Transf. 2022, 58, 1997–2007. [Google Scholar] [CrossRef]
- Borja, H.; Mariano, M.; Prashant, G. Numerical study of airflow regimes and instabilities produced by the swirl generation chamber in counter-current spray dryers. Chem. Eng. Res. Des. 2021, 176, 89–101. [Google Scholar]
- Manimaran, R.; Kumar, M.M.K.; Shankar, V.H. Study on novel nano mahua methyl ester powered DI diesel engine preheated with a thermoelectric waste heat recovery system. Energy Sources Part A Recovery Util. Environ. Eff. 2021, 43, 3251–3265. [Google Scholar]
- Jangam, S.V. Role of Drying Technology in The Promotion of Global Drying R&D. Dry. Technol. 2012, 30, 327. [Google Scholar]
- Kong, N.H. Simulation of Hot Air Drying on Corn Kernel Based on Three Dimension Solid Model; Northeastern University: Shenyang, China, 2013. [Google Scholar]
- Zheng, F. Research and Experiment on Key Technologies and Equipment of Grain Multi-Field Collaborative Drying; South China Agricultural University: Guangzhou, China, 2018. [Google Scholar]
- Chi, G.L. Air Drying Simulation System for Corn Drying; Jilin University: Changchun, China, 2004. [Google Scholar]
- Bishnoi, R.; Aharwal, K.R. Experimental and theoretical analysis of mass transfer in a refrigerated food storage. Heat Mass Transf. 2022, 58, 1845–1855. [Google Scholar] [CrossRef]
- Chokphoemphun, S.; Chokphoemphum, S. Moisture content prediction of paddy drying in a fluidized-bed drier with a vortex flow generator using an artificial neural network. Appl. Therm. Eng. 2018, 145, 630–636. [Google Scholar] [CrossRef]
- Sureshkumar, R.; Kale, S.R.; Dhar, P.L. Heat and mass transfer processes between a water spray and ambient air-I. Exp. Data. Appl. Therm. Eng. 2007, 28, 349–360. [Google Scholar] [CrossRef]
- Lowrey, S.; Sun, Z. Experimental investigation and numerical modelling of a compact wet air-to-air plate heat exchanger. Appl. Therm. Eng. 2017, 131, 89–101. [Google Scholar] [CrossRef]
- Chang, S.J.; Wi, S.; Lee, J.; Kim, S. Thermal performance analysis of phase change materials composed of double layers considering heating and cooling period. J. Ind. Eng. Chem. 2019, 72, 255–264. [Google Scholar] [CrossRef]
- Loo, L.; Maaten, B.; Siirde, A.; Pihu, T.; Konist, A. Experimental analysis of the combustion characteristics of Estonian oil shale in air and oxy-fuel atmospheres. Fuel Process. Technol. 2015, 134, 317–324. [Google Scholar] [CrossRef]
- Chu, Z.; Yang, J.; Li, X.; Song, Y. Heat and mass transfer engorgement of vibrating fluidized bed. J. Therm. Sci. 1994, 3, 257–262. [Google Scholar] [CrossRef]
- Ibrahim, D.; Mehmet, P. The thin-layer drying characteristics of corn. J. Food Eng. 2003, 60, 125–130. [Google Scholar]
- Yin, W.D.; Li, B.; Wu, Y.; Yang, H.; Liu, Q.; Lu, J.; Zhao, J. Model of coal slime combustion behavior in CFB boiler. J. China Coal Soc. 2015, 40, 1628–1633. [Google Scholar]
- Daming, S.; Rainer, N.; Lothar, R. Wall-to-bed heat transfer in circulating fluidized beds. Chem. Eng. Process. Process Intensif. 1998, 37, 287–293. [Google Scholar]
- Liu, Q.; Bakker-Arkema, F.W. A model-predictive controller for grain drying. J. Food Eng. 2001, 49, 321–326. [Google Scholar] [CrossRef]
- Lu, J.; Zhang, J.; Yue, G.; Liu, Q.; Yu, L.; Lin, X.; Li, W.; Tang, Y.; Luo, T.; Ge, R. Method of calculation of heat transfer coefficient of the heater in a circulating fluidized bed furnace. Heat Transf. Asian Res. 2002, 31, 540–550. [Google Scholar] [CrossRef]
- Hao, Z.H. The Development of Baffle Downer Dryer for Lignite Demoisture with High Temperature Flue Gas and the Research of the Key Technologies; Tsinghua University: Beijing, China, 2011. [Google Scholar]
- Syahrul, I.; Dincer, F. Thermodynamic modeling of fluidized bed drying of moist particles. Int. J. Therm. Sci. 2003, 42, 691–701. [Google Scholar] [CrossRef]
- Wu, G.; He, Y.; Luo, L.; Chen, W. Dynamic characterizations of gas–solid flow in a novel multistage fluidized bed via nonlinear analyses. Chem. Eng. J. 2021, 359, 1013–1023. [Google Scholar] [CrossRef]
- Wang, C.T.; Tian, S.X.; An, X.Z. The effects of drying parameters on drying characteristics, colorimetric differences, antioxidant components of sliced Chinese jujube. Heat Mass Transf. 2022, 58, 1561–1571. [Google Scholar] [CrossRef]
- Wang, C. Analysis of Corn Hot Air Drying and Influencing Factors; Northeastern University: Shenyang, China, 2020. [Google Scholar]
- Onwude, D.I.; Hashim, N.; Chen, G. Recent advances of novel thermal combined hot air drying of agricultural crops. Trends Food Sci. Technol. 2016, 57, 132–145. [Google Scholar] [CrossRef]
- Prakash, B.; Pan, Z. Effect of geometry of rice kernels on drying modeling results. Dry. Technol. 2012, 30, 801–807. [Google Scholar] [CrossRef]
- Henrik, T.; Kent, D.; Bo, L. Separation of drying and devolatilization during conversion of solid fuels. Combust. Flame 2004, 137, 242–250. [Google Scholar]
- Perez, J.H.; Tanaka, F.; Uchino, T. Comparative 3D simulation on moisture absorption and hygroscopic swelling in japonica rice grains under various isothermal soaking condition. Food Res. Int. 2011, 44, 2615–2623. [Google Scholar] [CrossRef]
- Huang, K.; Chen, X.F.; Chen, P.X.; Wang, F.H.; Tu, G.; Zhao, Y.; Liu, X.D.; Yang, D.Y. Simulation and experimental analysis of mass transfer drying in maize grains. J. Eng. Thermophys. 2017, 38, 193–198. [Google Scholar]
- Walton, L.R.; White, G.M.; Ross, I.J. A cellular diffusion based drying model for corn. Trans. ASAE 1988, 31, 279–0283. [Google Scholar] [CrossRef]
- Franz, W.; Michael, E.P.; Hermann, H. Temperatures in a fuel particle burning in a fluidized bed: The effect of drying, devolatilization, and char combustion. Combust. Flame 1997, 108, 302–314. [Google Scholar]
- Zhao, L.; Yang, J.; Du, T.; Wu, Z. A 3-Dimensional body fitted simulation of heat and mass transfer in rice kernel during hot air drying Process. Int. J. Food Eng. 2019, 15, 1–11. [Google Scholar] [CrossRef]
- Lu, J.; Tian, Y.; Peng, X.; Yue, G. Analysis of particles motion and convection heat transfer in circulating fluidized bed. J. Chem. Ind. Eng. 2003, 54, 1224–1229. [Google Scholar]
- Gao, K. Study of Heat and Mass Exchange and Energy Consumption of during Grain Drying; North China Electric Power University: Beijing, China, 2019. [Google Scholar]
- Liu, Q.; Bakker-Arkema, F.W. Stochastic modelling of grain drying: Part 2. Model development. J. Agric. Eng. Res. 1997, 66, 275–280. [Google Scholar] [CrossRef]
- Zare, D.; Jayas, D.S.; Singh, C.B. A Generalized Dimensionless Model for Deep Bed Drying of Paddy. Dry. Technol. 2012, 30, 44–51. [Google Scholar] [CrossRef]
- Khatchatourian, O.A.; Vielmo, H.A.; Bortolaia, L.A. Modelling and simulation of cross flow grain dryers. Biosyst. Eng. 2013, 116, 335–345. [Google Scholar] [CrossRef]
- Prommas, R.; Rattanadecho, P.; Cholaseuk, D. Energy and exergy analyses in drying process of porous edia using hot air. Int. Commun. Heat Mass Transf. 2010, 37, 372–378. [Google Scholar] [CrossRef]
- Motevali, A.; Minaei, S.; Khoshtagaza, M.H. Evaluation of energy consumption in different drying methods. Energy Convers. Manag. 2011, 52, 1192–1199. [Google Scholar] [CrossRef]
- Sivakumar, R.; Elayaperumal, A. Studies on combined cooling and drying of agro products using air cooled internal heat recovered vapour absorption system. Appl. Therm. Eng. 2015, 97, 100–108. [Google Scholar] [CrossRef]
- Zhu, J.Y.; Wang, Q.M. Analysis of hot air drying characteristics of corn seeds considering the effect of flow field. Mod. Food 2022, 28, 164–167. [Google Scholar] [CrossRef]






| Numerical Value | |
|---|---|
| Corn moisture Yw-bed, % | 22 |
| The moisture content of the target product, % | 14 |
| Dry base density, kg/m3 | 1150 |
| Moisture density, kg/m3 | 1000 |
| The real density of corn particles, kg/m3 | 1117 |
| The initial temperature of corn to be processed Tbed, °C | −15 |
| Single corn weighs approximately, g | 0.4 |
| Bulk density, kg/m3 | 670 |
| Specific heat capacity of corn particle Cpc, kJ/kg · K | 2.00 |
| Specific heat capacity of moisture Cpw, kJ/kg · K | 4.18 |
| Latent heat of vaporization of free moisture rh, kJ/kg | 2257 |
| The heat of dissolution of ice Ih, kJ/kg | 335 |
| Structure and Operation Parameters | Numerical Value |
|---|---|
| The total diameter of drying tower D, m | 5 |
| Total height of drying tower, m | 18 |
| Total drying volume, m3 | 339.29 |
| The true density of corn kernels, kg/m3 | 1100–1200 |
| Complete stacking residence time, s | 21,054 |
| Processing G, kg/s | 8.38 |
| Speed of corn movement, mm/s | 0.85 |
| True corn weight, kg/s | 6.54 |
| Initial moisture weight, Yinitial water, kg/s | 1.84 |
| Product moisture weight, Yproduct-water, kg/s | 1.06 |
| evaporation, kg/s | 0.78 |
| Energy dissipation of evaporative moisture, kW | 1759.33 |
| Diameter of central hot air d, m | 1 |
| The cross-section area of corn circulation S, m2 | 18.85 |
| Hot wind flow rate q, Nm3/h | 71,000 |
| Hot air humidity Yhot wind, % | 0 |
| Accumulation porosity | 0.4 |
| Parameter | First (L = 5.3 m) | Second (L = 4.7 m) | Third (L = 4 m) |
|---|---|---|---|
| Transverse circulation area of hot air S, m2 | 49.95 | 18.85 | 37.70 |
| Hot air inlet temperature Tgas in °C | 160 | 140 | 120 |
| Hot air inlet enthalpy Hgas in, kJ/kg | 161.6 | 141.4 | 121.2 |
| Apparent velocity υ, m/s | 0.57 | 0.62 | 0.49 |
| Corn contact time ttime, s | 3.49 | 3.24 | 4.07 |
| Gas-solid contact area Sbed, m2 | 383.11 | 315.86 | 337.36 |
| Hot air outlet temperature Tgas out, °C | 65 (66) | 82 (84) | 66.7 (68) |
| Hot air outlet enthalpy Hgas out, kJ/kg | 65.65 | 82.82 | 67.37 |
| Hot air release Qreleased, kJ/s | 1916.95 | 1170.35 | 766.49 |
| Mean hot air temperature taverage, °C | 112.5 | 111 | 93.35 |
| The average temperature difference between corn and hot air t, °C | 107.1 | 79.35 | 48.65 |
| Convective heat transfer coefficient h, W/m2 K | 46.7 | 46.7 | 46.7 |
| Heat transfer Q, °C, kW | 1916.13 | 1170.48 | 766.46 |
| The heat capacity of corn and moisture absorbs heat Qc, kW | 847.75 | 239.03 | 283.03 |
| Moisture evaporation m, kg/s | 0.20 | 0.41 | 0.21 |
| Absolute humidity Áw, % | 10.13 | 20.93 | 15.24 |
| Relative humidity RH, % | 43.84 | 90.59 | 65.97 |
| Corn moisture Yw-bed, % | 20.10 | 15.85 | 13.46 (14) |
| Energy efficiency η, % | 60.15 | 41.97 | 44.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Zhang, S.; Fan, H.; Zhang, M.; Hu, N.; Yang, H. Modeling and Experimental Study on Drying Characteristics of Corn Particles with Hot Air in Downward Moving Bed. Fluids 2023, 8, 63. https://doi.org/10.3390/fluids8020063
Wang H, Zhang S, Fan H, Zhang M, Hu N, Yang H. Modeling and Experimental Study on Drying Characteristics of Corn Particles with Hot Air in Downward Moving Bed. Fluids. 2023; 8(2):63. https://doi.org/10.3390/fluids8020063
Chicago/Turabian StyleWang, Hairui, Shuangming Zhang, Haodong Fan, Man Zhang, Nan Hu, and Hairui Yang. 2023. "Modeling and Experimental Study on Drying Characteristics of Corn Particles with Hot Air in Downward Moving Bed" Fluids 8, no. 2: 63. https://doi.org/10.3390/fluids8020063