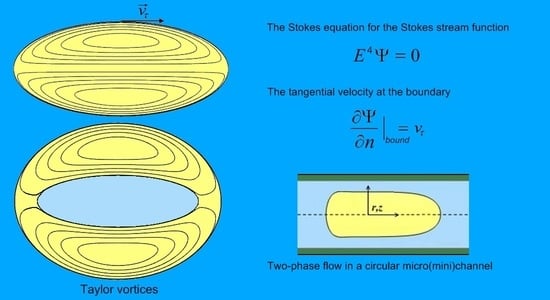
Mathematical Model for Axisymmetric Taylor Flows Inside a Drop
Abstract
:1. Introduction
2. Problem Formulation
3. Problem Solution
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Derivation of a Stokes Stream Function
References
- Kreutzer, M.T.; Kapteijn, F.; Moulijn, J.A.; Heiszwolf, J.J. Multiphase monolith reactors: Chemical reaction engineering of segmented flow in microchannels. Chem. Eng. Sci. 2005, 60, 5895–5916. [Google Scholar] [CrossRef]
- Bauer, T.; Schubert, M.; Lange, R.; Abiev, R.S. Intensification of heterogeneous catalytic gas-fluid interactions in reactors with a multichannel monolithic catalyst. Russ. J. Appl. Chem. 2006, 79, 1047–1056. [Google Scholar] [CrossRef]
- Liu, H.; Vandu, C.O.; Krishna, R. Hydrodynamics of Taylor Flow in Vertical Capillaries: FlowRegimes, Bubble Rise Velocity, Liquid Slug Length, and Pressure Drop. Ind. Eng. Chem. Res. 2005, 44, 4884–4897. [Google Scholar] [CrossRef]
- Ghaini, A.; Kashid, M.N.; Agar, D.W. Effective interfacial area for mass transfer in the liquid–liquid slug flow capillary microreactors. Chem. Eng. Process. Process Intensif. 2010, 49, 358–366. [Google Scholar] [CrossRef]
- Abiev, R.S. Gas-liquid and gas-liquid-solid mass transfer model for Taylor flow in micro (milli) channels: A theoretical approach and experimental proof. Chem. Eng. J. Adv. 2020, 4, 100065. [Google Scholar] [CrossRef]
- Shao, N.; Gavriilidis, A.; Angeli, P. Mass transfer during Taylor flow in microchannels with and withoutchemical reaction. Chem. Eng. J. 2010, 160, 873–881. [Google Scholar] [CrossRef]
- Abiev, R.S.; Butler, C.; Cid, E.; Lalanne, B.; Billet, A.-M. Mass transfer characteristics and concentration field evolution for gas-liquid Taylor flow in milli channels. Chem. Eng. Sci. 2019, 207, 1331–1340. [Google Scholar] [CrossRef] [Green Version]
- Butler, C.; Cid, E.; Billet, A.-M. Modelling of mass transfer in Taylor flow: Investigation with the PLIF-I technique. Chem. Eng. Res. Des. 2016, 115, 292–302. [Google Scholar] [CrossRef] [Green Version]
- Butler, C.; Lalanne, B.; Sandmann, K.; Cid, E.; Billet, A.-M. Mass transfer in Taylor flow: Transfer rate modelling from measurements at the slug and filmscale. Int. J. Multiph. Flow 2018, 105, 185–201. [Google Scholar] [CrossRef] [Green Version]
- Dietrich, N.; Loubière, K.; Jimenez, M.; Hébrard, G.; Gourdon, C. A new directtechnique for visualizing and measuring gas–liquid mass transfer aroundbubbles moving in a straight millimetric square channel. Chem. Eng. Sci. 2013, 100, 172–182. [Google Scholar] [CrossRef] [Green Version]
- Bretherton, F.P. The motion of long bubbles in tubes. J. Fluid Mech. 1961, 10, 166–188. [Google Scholar] [CrossRef]
- Klaseboer, E.; Gupta, R.; Manica, R. An extended Bretherton model for long Taylor bubbles at moderate capillary numbers. Phys. Fluids 2014, 26, 032107. [Google Scholar] [CrossRef]
- Falconi, C.J.; Lehrenfeld, C.; Marschall, H.; Meyer, C.; Abiev, R.S.; Bothe, D.; Reusken, A.; Schluter, M.; Wörner, M. Numerical and experimental analysis of local flow phenomena in laminar Taylor flow in a square mini-channel. Phys. Fluids 2016, 28, 012109. [Google Scholar] [CrossRef]
- Dore, V.; Tsaoulidis, D.; Angeli, P. Mixing patterns in water plugs during water/ionic liquid segmented flow in microchannels. Chem. Eng. Sci. 2012, 80, 334–341. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Angeli, P. Experimental and numerical hydrodynamic studies of ionic liquid-aqueous plug flow in small channels. Chem. Eng. J. 2017, 15, 17–736. [Google Scholar] [CrossRef]
- Marschall, H.; Falconi, C.; Lehrenfeld, C.; Abiev, R.; Wörner, M.; Reusken, A.; Bothe, D. Transport Processes at Fluidic Interfaces. In Direct Numerical Simulations of Taylor Bubbles in a Square Mini-Channel: Detailed Shape and Flow Analysis with Experimental Validation; Springer: Berlin/Heidelberg, Germany, 2017; pp. 663–679. [Google Scholar] [CrossRef]
- Meyer, C.; Hoffmann, M.; Schlüter, M. Micro-PIV analysis of gas–liquid Taylor flow in a vertical oriented square shaped fluidic channel. Int. J. Multiph. Flow 2014, 67, 140–148. [Google Scholar] [CrossRef]
- Kashid, M.; Platte, F.; Agar, D.; Turek, S. Computational modelling of slug flow in a capillary microreactor. J. Comput. Appl. Math. 2007, 203, 487–497. [Google Scholar] [CrossRef] [Green Version]
- Kashid, M.N.; Fernandez Rivas, D.; Agar, D.W.; Turek, S. On the hydrodynamics of liquid–liquid slug flow capillary microreactors. Asia-Pac. J. Chem. Eng. 2008, 3, 151–160. [Google Scholar] [CrossRef]
- Cherukumudi, A.; Klaseboer, E.; Khan, S.A.; Manica, R. Prediction of the shape and pressure drop of Taylor bubbles in circular tubes. Microfluid. Nanofluidics 2015, 19, 1221–1233. [Google Scholar] [CrossRef]
- Abiev, R.S. Analysis of local pressure gradient inversion and form of bubbles in Taylor flow in microchannels. Chem. Eng. Sci. 2017, 174, 403–412. [Google Scholar] [CrossRef]
- Makeev, I.V.; Popov, I.Y.; Abiev, R.S. Analytical solution of Taylor circulation in a prolate ellipsoid droplet in the frame of 2D Stokes equations. Chem. Eng. Sci. 2019, 207, 145–152. [Google Scholar] [CrossRef]
- Van Der Woude, D.; Clercx, H.J.H.; Van Heijst, G.J.F.; Meleshko, V.V. Stokes flow in a rectangular cavity by rotlet forcing. Phys. Fluids 2007, 19, 083602. [Google Scholar] [CrossRef]
- Gürcan, F.; Gaskell, P.H.; Savage, M.D.; Wilson, M. Eddy genesis and transformation of Stokes flow in a double-lid driven cavity. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2003, 217, 353–364. [Google Scholar] [CrossRef]
- Krasnopolskaya, T.S.; Meleshko, V.; Peters, G.; Meijer, H.E.H. Steady stokes flow in an annular cavity. Q. J. Mech. Appl. Math. 1996, 49, 593–619. [Google Scholar] [CrossRef]
- Saatdjian, E.; Midoux, N.; Andreé, J.C. On the solution of Stokes’ equations between confocal ellipses. Phys. Fluids 1994, 6, 3833–3846. [Google Scholar] [CrossRef]
- Tosi, N.; Martinec, Z.; Brajanovski, M.; Müller, T.M.; Gurevich, B. Semi-analytical solution for viscous Stokes flow in two eccentrically nested spheres. Geophys. J. Int. 2007, 170, 1015–1030. [Google Scholar] [CrossRef] [Green Version]
- Smolkina, M.O.; Popov, I.Y.; Blinova, I.V.; Milakis, E. On the metric graph model for flows in tubular nanostructures. Nanosyst. Phys. Chem. Math. 2019, 10, 6–11. [Google Scholar] [CrossRef] [Green Version]
- Popov, I.Y.; Lobanov, I.S.; Popov, S.I.; Popov, A.I.; Gerya, T.V. Practical analytical solutions for benchmarking of 2-D and 3-D geodynamic Stokes problems with variable viscosity. Solid Earth 2014, 5, 461–476. [Google Scholar] [CrossRef] [Green Version]
- Driesen, C.H.; Kuerten, J. An accurate boundary-element method for Stokes flow in partially covered cavities. Comput. Mech. 2000, 25, 501–513. [Google Scholar] [CrossRef]
- Happel, J.; Brenner, H. Low Reynolds Number Hydrodynamics: With Special Applications to Particulate Media; Prentice-Hall: Upper Saddle River, NJ, USA, 1965; p. 553. [Google Scholar]
- Abiev, R.S. Simulation of the slug flow of a gas-liquid system in capillaries. Theor. Found. Chem. Eng. 2008, 42, 105–117. [Google Scholar] [CrossRef]
- Abiev, R.S. Circulation and bypass modes of the slug flow of a gas-liquid mixture in capillaries. Theor. Found. Chem. Eng. 2009, 43, 298–306. [Google Scholar] [CrossRef]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Makeev, I.V.; Abiev, R.S.; Popov, I.Y. Mathematical Model for Axisymmetric Taylor Flows Inside a Drop. Fluids 2021, 6, 7. https://doi.org/10.3390/fluids6010007
Makeev IV, Abiev RS, Popov IY. Mathematical Model for Axisymmetric Taylor Flows Inside a Drop. Fluids. 2021; 6(1):7. https://doi.org/10.3390/fluids6010007
Chicago/Turabian StyleMakeev, Ilya V., Rufat Sh. Abiev, and Igor Yu. Popov. 2021. "Mathematical Model for Axisymmetric Taylor Flows Inside a Drop" Fluids 6, no. 1: 7. https://doi.org/10.3390/fluids6010007