Mean Drift Forces on Vertical Cylindrical Bodies Placed in Front of a Breakwater
Abstract
:1. Introduction
1.1. Numerical/Theoretical Calculation Methods
1.2. Experimental Validation Tests
1.3. Body-Breakwater Simulation Methods
1.4. Interaction Phenomena Calculation Methods
2. Hydrodynamic Formulation
2.1. Velocity Potential: Matched Axisymmetric Eigenfunctions Expansions
- the Laplace equation:
- the combined linear kinematic and dynamic boundary condition on the free surface:
- the zero–velocity condition on the flat sea bottom:
- the kinematic conditions on the wetted surface of all the bodies of the array:
2.2. Velocity Potential: The Sink-Source Technique
3. Mean Drift Forces Calculation Methods
3.1. The Momentum Method
3.2. The Direct integration Method
3.3. The Image Method Applied on the Drift Forces
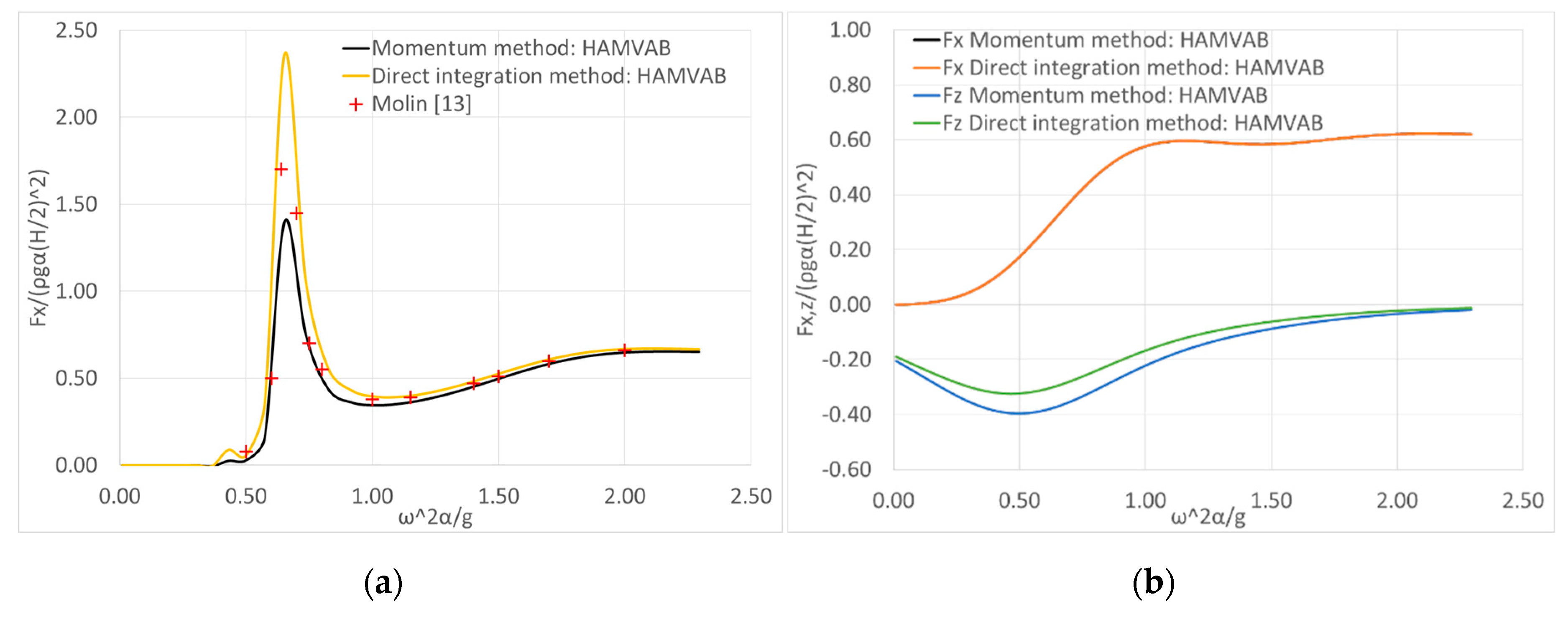
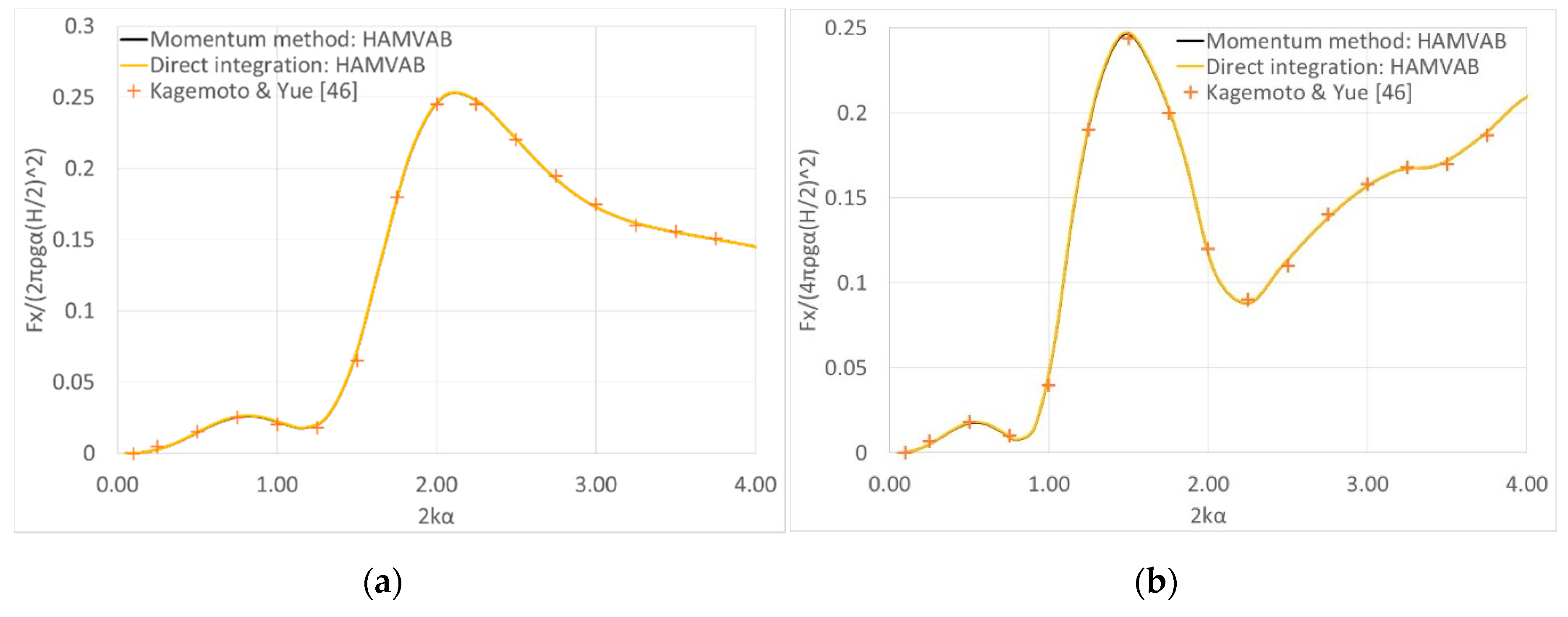
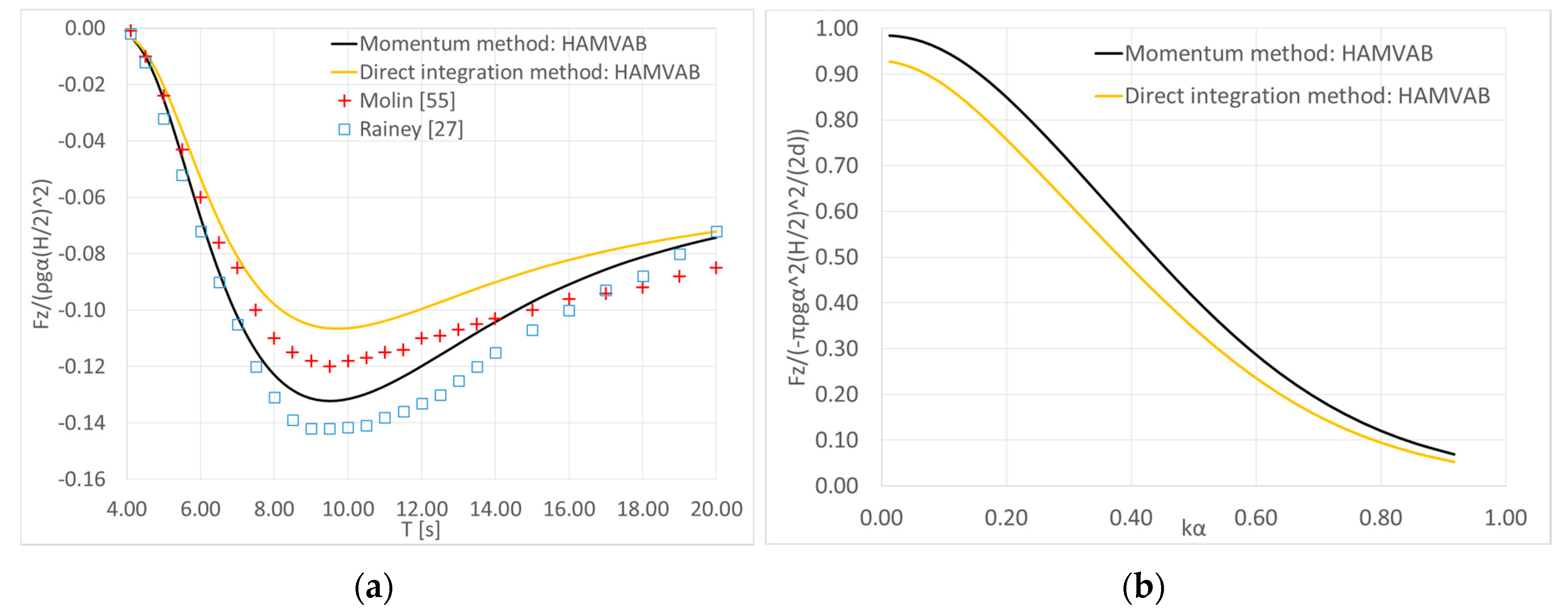
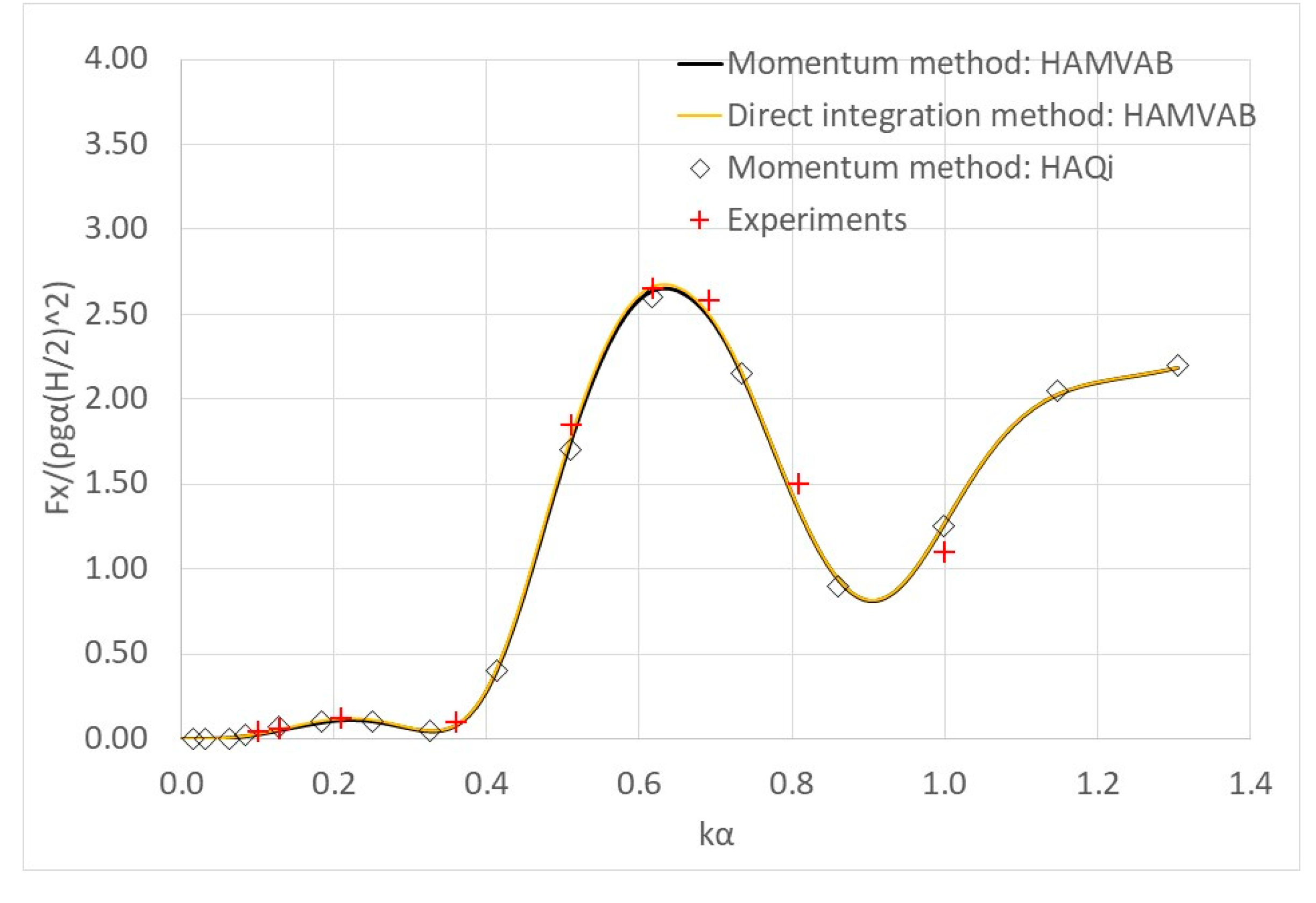
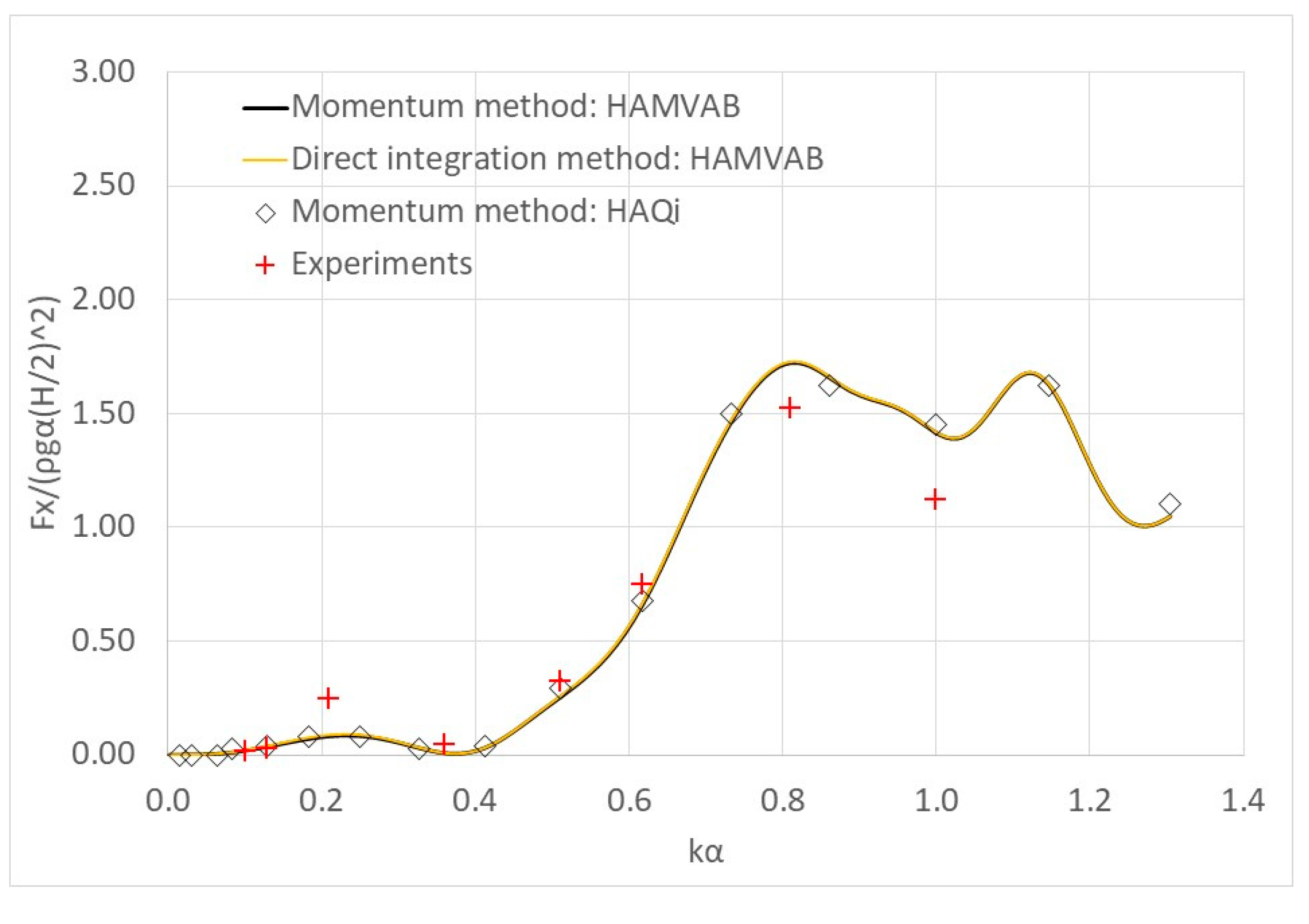
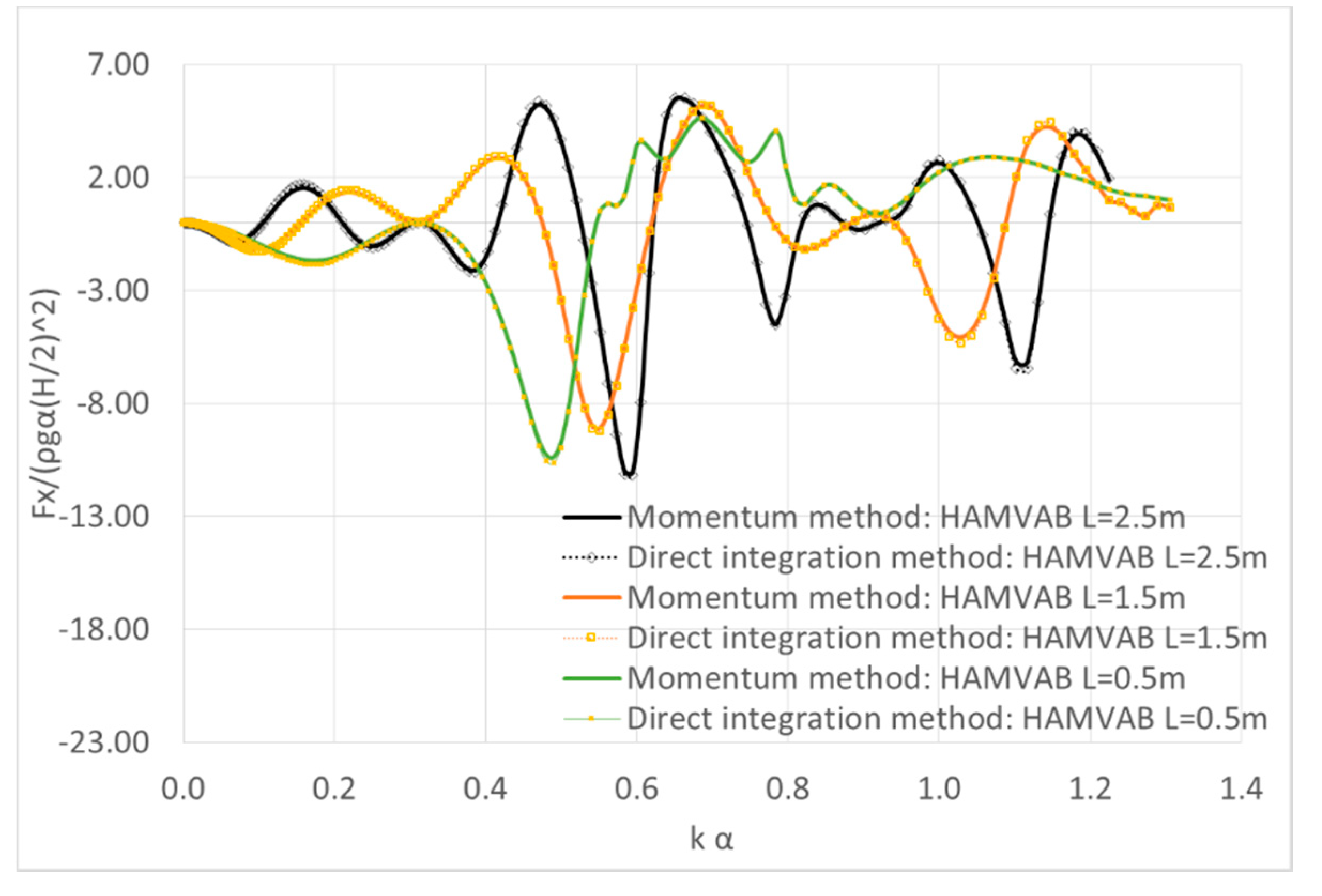
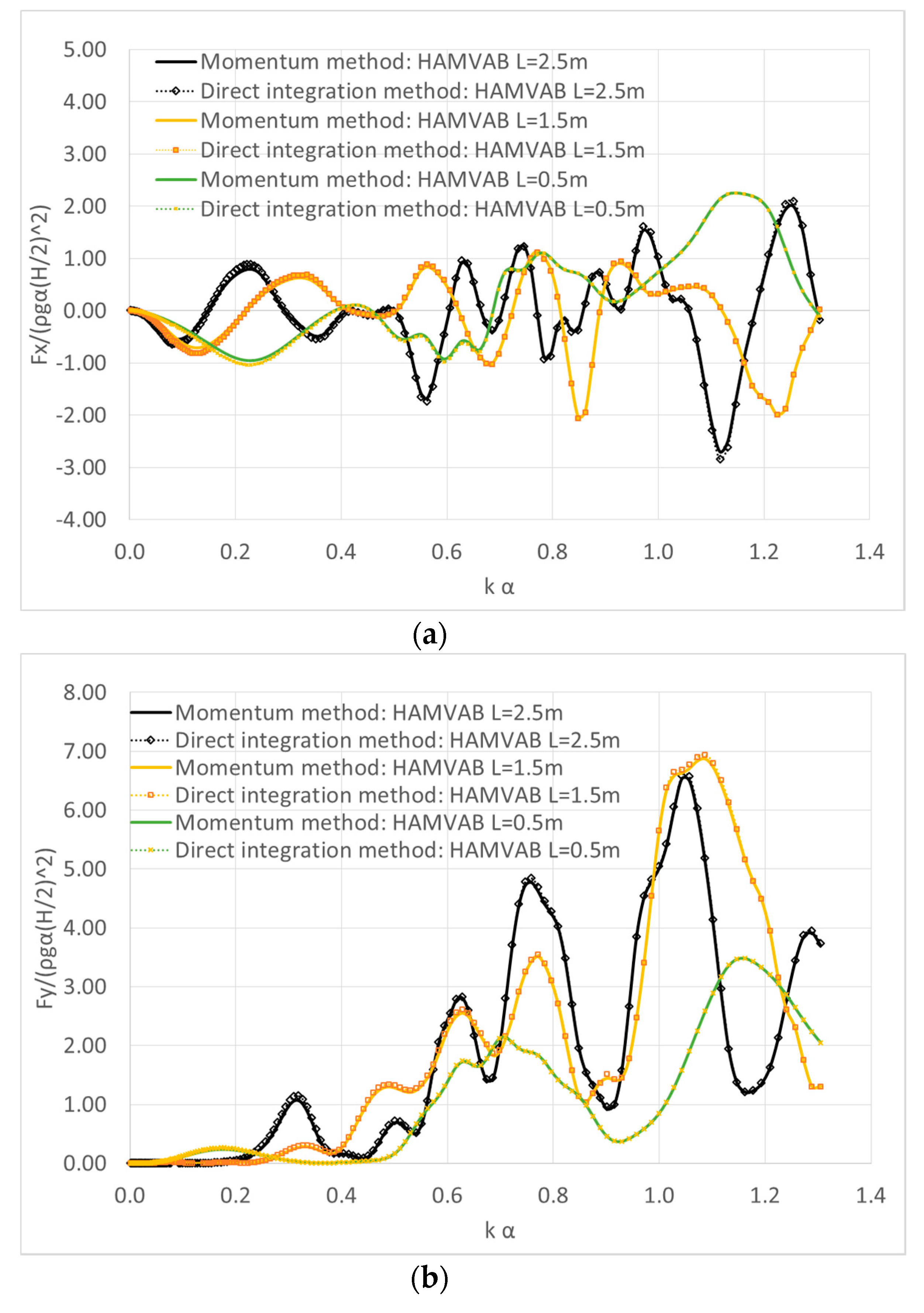
4. Results Validation
5. Experimental Campaign
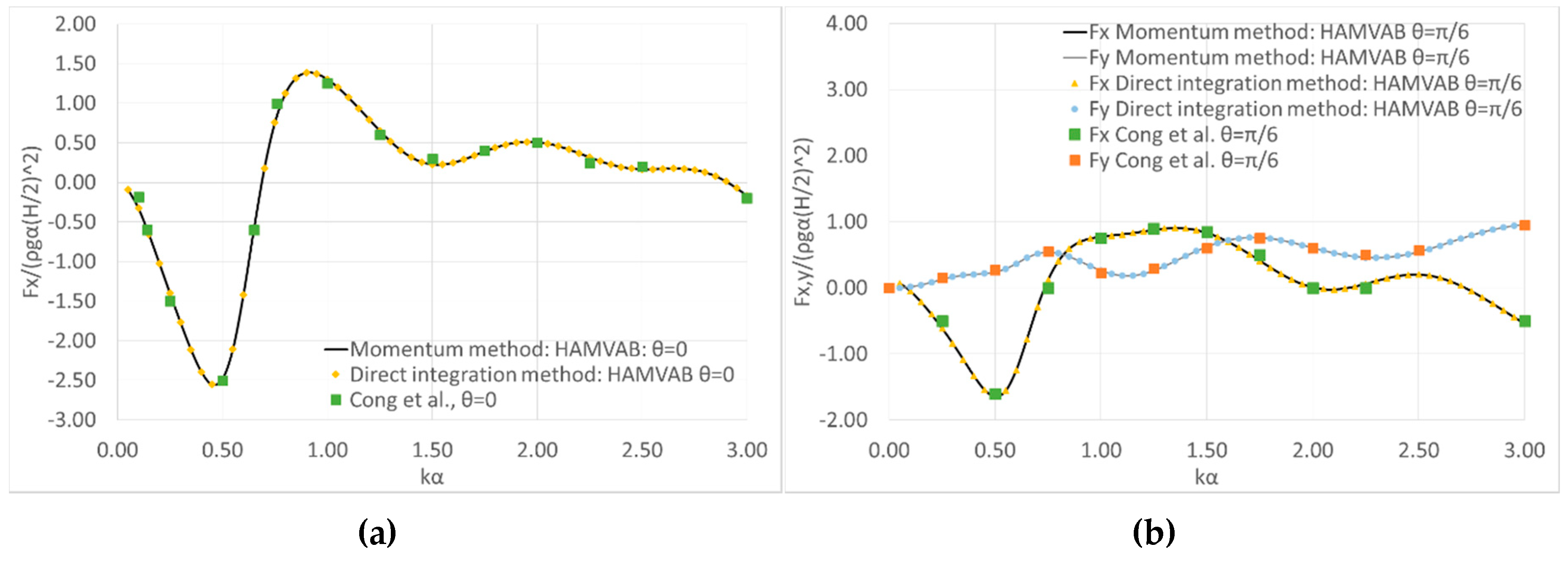
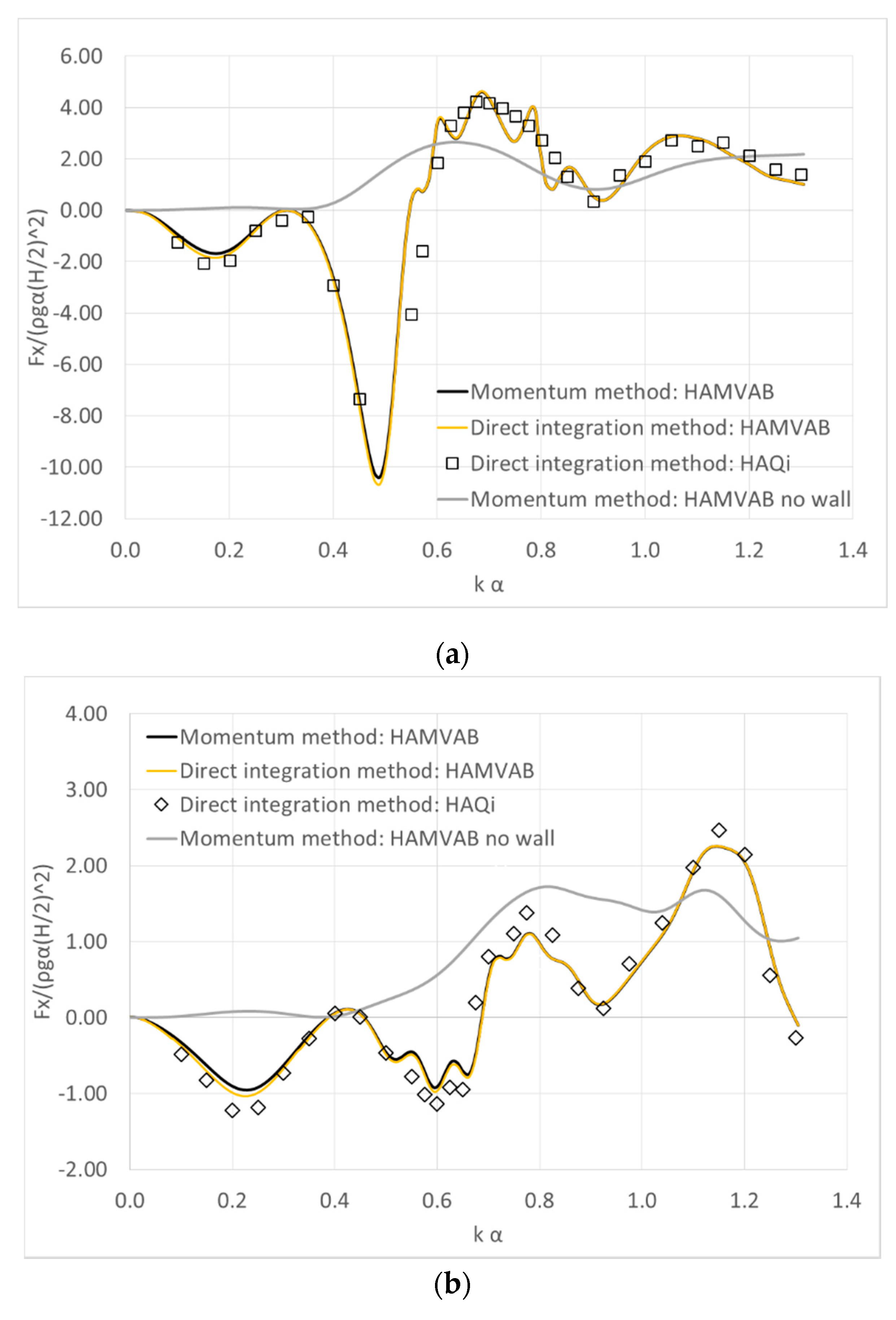
6. Array of Cylinders in Front of a Breakwater
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| N | Number of bodies |
| d | Water depth |
| hk | Distance from the sea bed of the k body |
| α | Radius of the examined body |
| ω | Wave frequency |
| k | Wave number |
| H/2 | Wave amplitude |
| θ | Wave heading angle |
| rk,θk,zk | Local co-ordinate system of the k body |
| Lk | Distance between adjacent bodies |
| Lwk | Distance between the closest to the wall bodies from the breakwater |
| Φ | Time harmonic complex velocity potential |
| Velocity potential of the undisturbed incident harmonic wave | |
| Scattered velocity potential for the k body | |
| Radiation velocity potential resulting from the forced p body motion | |
| Diffraction velocity potential for the k body | |
| Ω | Fluid domain |
| SF | Undisturbed free water surface |
| SB | Sea bottom surface |
| Mean wetted surface of the k body | |
| Unit normal vector | |
| δk,p | Kronecker’s symbol |
| Amplitude of the translation and rotation motion of the k body | |
| Unknown diffraction coefficient | |
| Unknown motion radiation coefficient | |
| I | The infinite ring element around the k body |
| II | The ring element below the k body |
| Qj | Singularity strength |
| G | Green function |
| xk,yk,zk,ξ,n,ζ | Rectangular coordinates of the k body |
| P | Number of plane elements |
| Fluid pressure on the k body | |
| Finite control volume of the k body | |
| ρ | Water density |
| P | Linear momentum of the fluid in the control volume |
| g | Gravity acceleration |
| U | Velocity of the boundary surface |
| ζ | Wave elevation |
| Mean second order drift forces | |
| Time dependent part of the vertical control surface | |
| Contour of the intersection of with the (x,y) plane | |
| Static water line | |
| M | Generalized mass matrix |
| Vector of the first order translation | |
| Rotational transformation matrix | |
| Vector of the first order translational acceleration of body’s center of gravity | |
| ζk | Relative wave elevation of first order |
| Vertical distance of the center of gravity from the sea bed |
Appendix A
References
- Havelock, T.H. The pressure of water waves upon a fixed obstacle. In Proceedings of the Royal Society of London; Series A, Mathematical and Physical Sciences; Royal Society: London, UK, 1940; Volume 175, pp. 409–421. [Google Scholar]
- Emmerhoff, O.J.; Sclavounos, P.D. The simulation of slow-drift motions of offshore structures. Appl. Ocean Res. 1996, 18, 55–64. [Google Scholar] [CrossRef]
- Martin, J.; Kuo, C. Calculations for the steady tilt of semi-submersibles in regular waves. Trans. RINA 1979, 121, 87–101. [Google Scholar]
- Hineno, M.; Takegawa, H.; Oda, T.; Abe, M. The effect of low frequency roll motion on under-deck clearance of a semi-submersible platform. In Proceedings of the 2nd International Conference on Stability of Ships and Ocean Vehicles, Tokyo, Japan, 24–29 October 1982. [Google Scholar]
- Stansberg, C.T. Slow-drift pitch motions and air-gap observed from model testing with moored semi-submersibles. In Proceedings of the 26th International Conference on Ocean, Offshore and Arctic Engineering (OMAE), San Diego, CA, USA, 10–15 June 2007; Volume 1. [Google Scholar]
- Van der Valk, C.A.C.; Watson, A. Mooring OF LNG carriers to a weathervaning floater—Side-by-side or stern-by-bow. In Proceedings of the 2005 Offshore Technology Conference, Houston, TX, USA, 2–5 May 2005; p. 17154. [Google Scholar]
- Newman, J.N. Second order, slowly varying forces on vessels in irregular waves. In Proceedings of the International Symposium on Dynamics of Marine Vehicles and Structures in Waves, London, UK, 1–5 April 1974; pp. 182–186. [Google Scholar]
- Maruo, H. The drift of a body floating in waves. J. Ship Res. 1960, 4, 1–10. [Google Scholar]
- Newman, J.N. The drift force and moment on ships in waves. J. Ship Res. 1967, 11, 51–60. [Google Scholar]
- Faltinsen, O.M.; Michelsen, F.C. Motions of large structures in waves at zero Froude number. In Proceedings of the International Symposium on Dynamics of Marine Vehicles and Structures in Waves, London, UK, 1–5 April 1974; pp. 91–106. [Google Scholar]
- Lee, C.M.; Newman, J.N. The vertical man force and moment of submerged bodies under waves. J. Ship Res. 1971, 15, 231–245. [Google Scholar]
- Sclavounos, P.D. The Vertical Wave Drift Force on Floating Bodies. In Proceedings of the 2nd International Workshop on Water Waves and Floating Bodies, Bristol, UK, 16–19 March 1987. [Google Scholar]
- Molin, B. On second-order motion and vertical drift forces for three-dimensional bodies in regular waves. In Proceedings of the International Workshop on Ship and Platform Motion, Berkeley, CA, USA, 26–28 October 1983; pp. 344–357. [Google Scholar]
- Mavrakos, S.A. The vertical drift force and pitch moment on axisymmetric bodies in regular waves. Appl. Ocean Res. 1988, 10, 207–218. [Google Scholar] [CrossRef]
- Mavrakos, S.A. Mean drift loads on multiple vertical axisymmetric bodies in regular waves. In Proceedings of the 5th International Offshore and Polar Engineering Conference, The Hague, The Netherlands, 11–16 June 1995. [Google Scholar]
- Kashiwagi, M. Added resistance, wave-induced steady sway force and yaw moment on an advancing ship. J. Schiffstechnik 1992, 39, 3–16. [Google Scholar]
- Kashiwagi, M.; Ohkusu, M. Study on the wave-induced steady force and moment. J. Soc. Nav. Archit. Jpn. 1993, 173, 185–194. [Google Scholar] [CrossRef]
- Pinkster, J.A.; Van Oortmerssen, G. Computation of the first and second order wave forces on oscillating bodies in regular waves. In Proceedings of the 2nd International Conference on Numerical Ship Hydrodynamics, Berkeley, CA, USA, 19–21 September 1977. [Google Scholar]
- Standing, R.G.; Dacunha, N.M.C. Slowly-varying and mean second-order wave forces on ships and offshore structures. In Proceedings of the 14th Symposium on Naval Hydrodynamics, Ann Arbor, MI, USA, 23–27 August 1982; pp. 279–318. [Google Scholar]
- Papanikolaou, A.; Zaraphonitis, G. On the improved method for the evaluation of second-order motions and loads on 3D floating bodies in waves. J. Schiffstechnik 1987, 34, 170–211. [Google Scholar]
- Zhao, R.; Faltinsen, O.M. Interaction between current, waves and marine structures. In Proceedings of the 5th International Conference on Numerical Ship Hydrodynamics, Hiroshima, Japan, 24–28 September 1990. [Google Scholar]
- Shao, Y.L. Numerical analysis of second-order mean wave forces by a stabilized higher order boundary element method. In Proceedings of the 37th International Conference on Ocean, Offshore and Arctic Engineering, (OMAE), Madrid, Spain, 17–22 July 2018. [Google Scholar]
- Chen, X.B. Hydrodynamic analysis for offshore LNG terminals. In Proceedings of the 2nd Offshore Hydrodynamics Symposium, Rio de Janeiro, Brazil, 14–15 April 2005. [Google Scholar]
- Rezend, F.; Li, X.; Chen, X.-B. Second order loads on LNG terminals in multi-directional sea in water of finite depth. In Proceedings of the 26th International Conference on Ocean, Offshore and Arctic Engineering (OMAE), San Diego, CA, USA, 10–15 June 2007; Volume 1. [Google Scholar]
- Cong, P.; Liu, Y. Local Enhancements of the mean drift wave force on a vertical column shielded by an exterior thin porous shell. J. Mar. Sci. Eng. 2020, 8, 349. [Google Scholar] [CrossRef]
- Higo, Y.; Ha, M.K. A study on added resistance of a restrained body with forward speed in waves. J. Soc. Nav. Archit. Jpn. 1991, 169, 75–83. [Google Scholar] [CrossRef] [Green Version]
- Rainey, R.C.T. A new equation for calculating wave loads on offshore structures. J. Fluid Mech. 1989, 204, 295–324. [Google Scholar] [CrossRef]
- Kobayashi, M.; Shimada, K.; Fujchira, T. Study on the dynamic response of a TLP in waves. In Proceedings of the 4th International Offshore Mechanics and Arctic Engineering Symposium; ASME: New York, NY, USA, 1985; Volume 1, pp. 29–35. [Google Scholar]
- Kashiwagi, M.; Endo, K.; Yamaguchi, H. Wave drift forces and moments on two ships arranged side by side in waves. Ocean Eng. 2005, 32, 529–555. [Google Scholar] [CrossRef]
- Konispoliatis, D.; Mavrakos, S. Mean drift loads on arrays of free floating OWC devices consisting of concentric cylinders. In Proceedings of the 29th International Workshop on Water Waves and Floating Bodies, Osaka, Japan, 30 March–2 April 2014. [Google Scholar]
- Ikoma, T.; Maeda, H.; Rheem, C.-K. Slowly varying wave drifting force on a very large floating structure in short crested waves. In Proceedings of the OCEANS 2000 MTS/IEEE Conference and Exhibition, Providence, RI, USA, 11–14 September 2000; Volume 1, pp. 533–539. [Google Scholar]
- Liu, Y.N.; Molin, B.; Kimmoun, O.; Remy, F.; Rouault, M.C. Experimental and numerical study of the effect of variable bathymetry on the slow-drift wave response of floating bodies. Appl. Ocean Res. 2011, 33, 199–207. [Google Scholar] [CrossRef]
- Mavrakos, S.A.; Katsaounis, G.M.; Nielsen, K.; Lemonis, G. Numerical performance investigation of an array of heaving wave power converters in front of a vertical breakwater. In Proceedings of the 14th International Offshore and Polar Engineering Conference (ISOPE 2004), Toulon, France, 23–28 May 2004. [Google Scholar]
- Mavrakos, S.A.; Katsaounis, G.M.; Kladas, A.; Kimoulakis, N. Numerical and experimental investigation of performance of heaving WECs coupled with DC generators. In Proceedings of the 9th European Wave and Tidal Energy Conference, Southampton, UK, 5–9 September 2011. [Google Scholar]
- McIver, P.; Porter, R. The motion of a freely floating cylinder in the presence of a wall and the approximation of resonances. J. Fluid Mech. 2016, 795, 581–610. [Google Scholar] [CrossRef] [Green Version]
- Teng, B.; Ning, D.Z. Wave diffraction from a uniform cylinder in front of a vertical wall. Ocean Eng. 2003, 21, 48–52. [Google Scholar]
- Teng, B.; Ning, D.Z.; Zhang, X.T. Wave radiation by a uniform cylinder in front of a vertical wall. Ocean Eng. 2004, 31, 201–224. [Google Scholar] [CrossRef]
- Zheng, S.; Zhang, Y. Wave diffraction from a truncated cylinder in front of a vertical wall. Ocean Eng. 2015, 104, 329–343. [Google Scholar] [CrossRef]
- Zheng, S.; Zhang, Y. Wave radiation from a truncated cylinder in front of a vertical wall. Ocean Eng. 2016, 111, 602–614. [Google Scholar] [CrossRef]
- Konispoliatis, D.N.; Mavrakos, S.A. Theoretical performance investigation of a vertical cylindrical oscillating water column device in front of a vertical breakwater. J. Ocean Eng. Mar. Energy 2019, 6, 1–13. [Google Scholar] [CrossRef]
- Konispoliatis, D.N.; Mavrakos, S.A.; Katsaounis, G.M. Theoretical Evaluation of the Hydrodynamic Characteristics of Arrays of Vertical Axisymmetric Floaters of Arbitrary Shape in front of a Vertical Breakwater. J. Mar. Sci. Eng. 2020, 8, 62. [Google Scholar] [CrossRef] [Green Version]
- Loukogeorgaki, E.; Boufidi, I.; Chatjigeorgiou, I. Performance of an array of oblate spheroidal heaving wave energy converters in front of a wall. Water 2020, 12, 188. [Google Scholar] [CrossRef] [Green Version]
- Twersky, V. Multiple scattering of radiation by an arbitrary configuration of parallel cylinders. J. Acoust. Soc. Am. 1952, 24, 42–46. [Google Scholar] [CrossRef]
- Mavrakos, S.A.; Koumoutsakos, P. Hydrodynamic interaction among vertical axisymmetric bodies restrained in waves. Appl. Ocean Res. 1987, 9, 128–140. [Google Scholar] [CrossRef]
- Mavrakos, S.A. Hydrodynamic coefficients for groups of interacting vertical axisymmetric bodies. Ocean Eng. 1991, 18, 485–515. [Google Scholar] [CrossRef]
- Kagemoto, H.; Yue, D.K.P. Interactions among multiple three-dimensional bodies in water waves: An exact algebraic method. J. Fluid Mech. 1986, 166, 189–209. [Google Scholar] [CrossRef]
- Linton, C.M.; Evans, D.V. The interaction of waves with arrays of vertical circular cylinders. J. Fluid Mech. 1990, 215, 549–569. [Google Scholar] [CrossRef]
- Mavrakos, S.A.; McIver, P. Comparison of methods for computing hydrodynamic characteristics of arrays of wave power devices. Appl. Ocean Res. 1997, 19, 283–291. [Google Scholar] [CrossRef]
- Wehausen, J.V.; Laitone, E.V. Surface Waves. In Encyclopedia of Physics; Springer: Berlin/Heidelberg, Germany, 1960; Volume 9. [Google Scholar]
- Mavrakos, S.A.; Bardis, L. Hydrodynamic Characteristics of Large Offshore Units. In Proceedings of the 3rd International Congress on Marine Technology (IMAM), Athens, Greece, 28 May–1 June 1984; pp. 505–513. [Google Scholar]
- Garrison, C.J. Hydrodynamics of large objects in the sea. Part I: Hydrodynamic analysis. J. Hydronautics 1974, 8, 5–12. [Google Scholar] [CrossRef]
- Garrison, C.J. Hydrodynamics of large objects in the sea. Part II: Motion of free floating bodies. J. Hydronautics 1975, 9, 58–63. [Google Scholar] [CrossRef]
- Konispoliatis, D.N.; Mavrakos, S.A. Wave power absorption by arrays of wave energy converters in front of a vertical breakwater. A theoretical study. Energies 2020, 13, 1985. [Google Scholar] [CrossRef] [Green Version]
- Mavrakos, S.A. User’s Manual for the Computer Code HAMVAB; Laboratory for Floating Bodies and Mooring Systems, National Technical University of Athens: Athens, Greece, 2001. [Google Scholar]
- Molin, B.; Lacaze, J.B. On approximations of the wave drift forces acting on semi-submersible platforms with heave plates. In Proceedings of the 35th International Conference on Ocean, Offshore and Arctic Engineering, Busan, Korea, 19–24 June 2016. [Google Scholar]
- Cong, P.; Chen, L.; Gou, Y. Hydrodynamic interaction among multiple columns in front of a vertical wall. Ocean Eng. 2020, 197, 106877. [Google Scholar] [CrossRef]
- Bardis, L.; Mavrakos, S.A. User’s Manual for the Computer Code HAQ; Laboratory for Floating Bodies and Mooring Systems, National Technical University of Athens: Athens, Greece, 1988. [Google Scholar]
- Mavrakos, S.A.; Mazarakos, T.P.; Konispoliatis, D.N. First- and second- order hydrodynamic effects and wave run-up on a four cylinder configuration at small forward speed. In Proceedings of the 9th International Congress on Mechanics (HSTAM), Limassol, Cyprus, 12–14 July 2010. [Google Scholar]

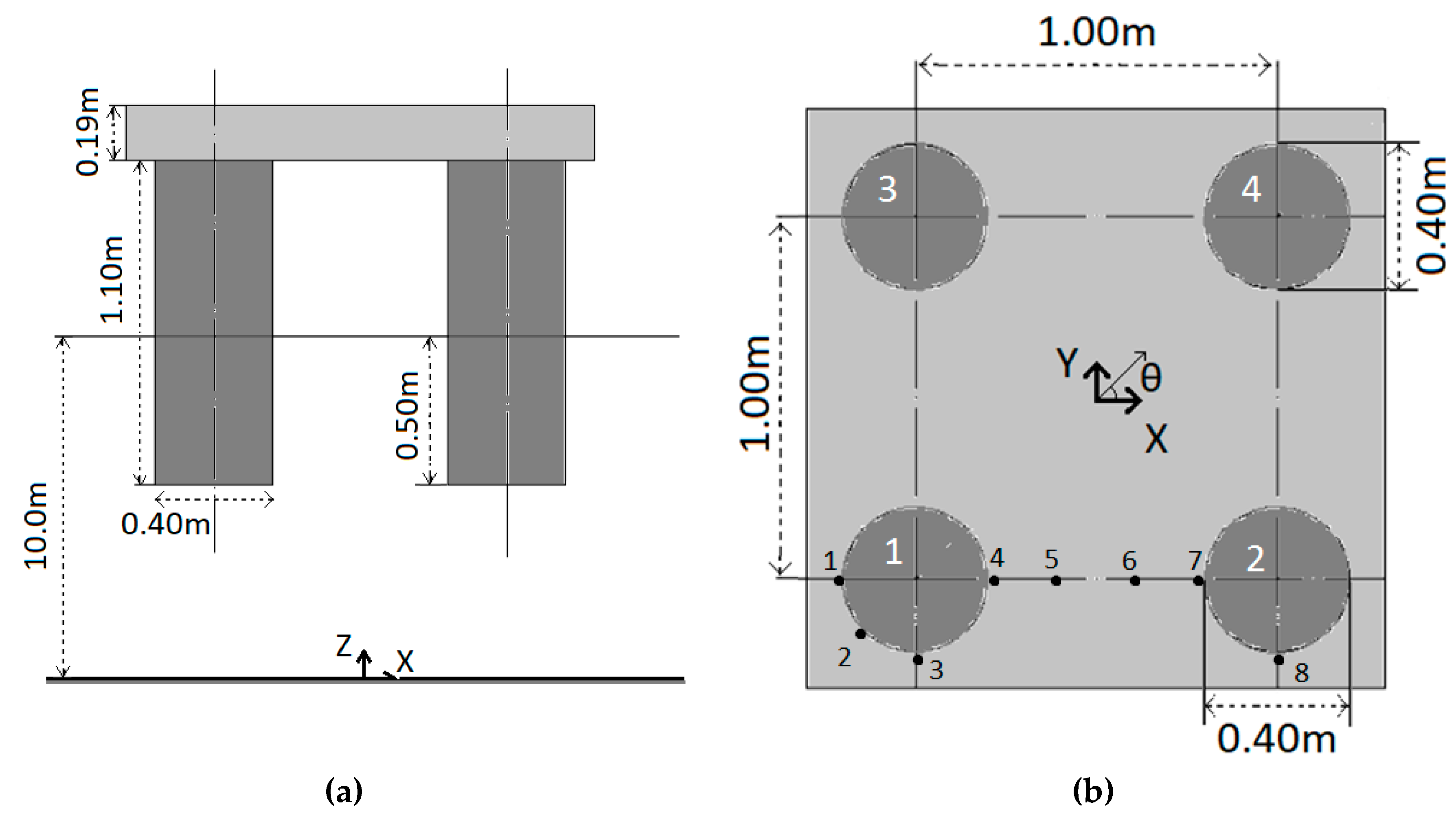



| Model Characteristics | Value |
|---|---|
| Weight (kg) | 160.000 |
| Displacement (kg) | 257.611 |
| Cylinder draught (m) | 0.50 |
| Cylinder height (m) | 1.10 |
| Cylinder diameter (m) | 0.40 |
| Distance between cylinders (m) | 1.00 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Konispoliatis, D.; Mavrakos, S. Mean Drift Forces on Vertical Cylindrical Bodies Placed in Front of a Breakwater. Fluids 2020, 5, 148. https://doi.org/10.3390/fluids5030148
Konispoliatis D, Mavrakos S. Mean Drift Forces on Vertical Cylindrical Bodies Placed in Front of a Breakwater. Fluids. 2020; 5(3):148. https://doi.org/10.3390/fluids5030148
Chicago/Turabian StyleKonispoliatis, Dimitrios, and Spyridon Mavrakos. 2020. "Mean Drift Forces on Vertical Cylindrical Bodies Placed in Front of a Breakwater" Fluids 5, no. 3: 148. https://doi.org/10.3390/fluids5030148
APA StyleKonispoliatis, D., & Mavrakos, S. (2020). Mean Drift Forces on Vertical Cylindrical Bodies Placed in Front of a Breakwater. Fluids, 5(3), 148. https://doi.org/10.3390/fluids5030148






